微电网中并联分布式发电单元的分散式控制算法研究

范 博，杨秦敏，刘文新

（1.浙江大学控制科学与工程学院，杭州 310027；2.理海大学电子与计算机工程学院，宾夕法尼亚 伯利恒 18015）

0 引言

随着能源需求的日益增长，利用可再生新能源的分布式发电技术得到了越来越多的关注[1-3]。然而，由于可再生能源的间歇性和随机性，导致传统电网的运行策略并不能很好地适应大规模分布式发电单元接入的要求[1]。

研究表明，通过微电网技术可以有效地解决大量分布式单元接入电网带来的问题。一般来说，微电网是一个由负载、储能系统以及分布式发电单元组成的小型电力系统，并可以工作在联网运行或者孤岛运行的状态[2]。

在微电网中，不同的分布式发电单元通过电力电子变换器接入其中[3]。相比于传统的同步发电机，以电力电子变换器为接口的分布式发电单元具有更高的控制灵活性。然而，由于电力电子变换器动态响应快以及可再生新能源的随机性，使得微电网具有惯性小、不确定性大的特点。因此，传统的电力系统和以电力电子变换器为主的微电网之间存在显著差异，使得传统电网的控制方法无法直接引入到微电网控制中[3]。

1 研究现状

1.1 微电网控制研究现状

在现有研究中，为了应对微电网控制带来的挑战，学者们提出了两类微电网的控制方案：

（1）通过虚拟同步技术，让微电网中分布式发电单元的动态特性表现的类似于传统的同步发电机[4-5]，从而提高微电网的虚拟惯性，传统电力系统的控制方案可以直接引入到微电网控制中[6]。但是此种控制方案不能完全体现现代电力电子技术的优势，特别是在响应速度和灵活性方面[7]。

（2）通过分层控制方案[8-9]将微电网建模为一组解耦的子系统，其中每个子系统由分布式发电单元、电力电子变换器和输出滤波器组成[10]。其中上层控制负责协调各个子系统之间的能量分配，从而保证整个微电网系统的稳定运行。下层控制则主要通过传统的双环PI 控制算法保证子系统母线电压和频率的稳定性。对于上层控制，考虑到各个子系统之间相互解耦，因此可以引入许多先进的分布式控制算法[11-15]，并得到良好的控制性能。然而，传统的基于双环PI 控制的下层控制算法的控制性能有限，难以实现期望的系统动态响应性能。

此外，在关于微电网控制的一些研究中，微电网被建模为多母线系统，其中每个母线只连接一个分布式发电单元[16-17]。在很多实际应用中，多个分布式发电单元可能会连接到一条母线上，组成并联分布式发电单元，例如光伏电站[18]和风电场[19]等。由于目前的多母线微电网控制算法没有考虑并联分布式发电单元的动态特性，因此现有的控制方案不能直接应用于此系统中。如果不能很好地协调并联的分布式发电单元，将可能导致微电网故障[20]。因此，研究微电网中并联分布式发电单元的控制方案是有必要的。

1.2 并联分布式发电单元控制研究现状

目前关于并联分布式发电单元控制方案的研究主要有两类[21]：

第一类是基于通讯网络的控制方案。包括3C控制[20]、集中控制[22]和主从控制[23]等，实现了良好的控制性能。然而，对于并联分布式发电单元，这些需要通信的控制方案不仅降低了系统的灵活性，还降低了可靠性[24]。

第二类是以下垂控制为主的分散式控制方案[25-28]。由于这些解决方案不需要分布式发电单元之间进行通讯，因此极大地提高了系统的灵活性和可靠性。然而，由于下垂控制的响应速度较慢，并且存在稳态控制误差，导致其无法直接应用于对控制性能有较高要求的场合[29]。

因此，为了提高并联分布式发电单元的控制性能，需要设计先进控制算法。

2 控制算法建模

2.1 并联分布式发电单元模型

并联分布式发电单元的系统拓扑结构如图1所示。系统中包含多个分布式发电单元和一个集总负载。每个分布式发电单元通过电力电子变换器和LC 滤波器连接到公共母线上[30]。

图1 并联分布式发电单元拓扑

考虑一个由n个分布式发电单元组成的系统，其模型为[21]：

式中：vo为母线电压；vj与ij分别为第j（j=1，2，…，n）个LC 滤波器输入电压与输入电流；ioj为第j个分布式发电单元输出电流；Δ，Δj为时变干扰，包含未建模动态、参数波动以及外部干扰等；Rj，Lj，Cj分别为测量得到第j个LC 滤波器参数。

2.2 控制目标

所设计的控制算法需要实现两个控制目标：

（1）负载电流按比例分配

该控制目标使负载电流在多个分布式发电单元之间按预先设定的比例分配，即对于所有i，j=1，2，…，n，i≠j，通过设计控制算法使尽量小，其中mj（0＜mj＜1）为系统中第j个分布式发电单元的电流分配比例，满足。

（2）母线电压调节

该控制目标是调节母线电压vo能更好地跟踪电压参考轨迹，其中VRMS为母线电压参考值的均方根值，ω 为电气角速度。

3 分散式控制算法设计

为了简化控制器设计，定义xj=ij/C，uj=（-vo-Rjij+vj）/LjC，以及dj=Δj/C，其中为总电容，uj和xj分别为控制输入和系统状态，并假设时变干扰d和dj及其有限阶导数有界[31]。之后，系统模型公式（1）可重写为：

进而，定义如下跟踪误差与滤波误差[32]为：

式中：k和kr为正常数。根据线性系统理论可知，随着趋向于0，eo，r也将趋向于0。考虑系统模型式（2）与式（3），可设计状态反馈控制率如下：

式中：kρ为正常数。需要注意的是，所设计的控制率仅需要分布式发电单元本地的电压电流信息以及参考轨迹，各个分布式发电单元之间不需要信息交互，因此所设计的控制算法是完全分散式的。

类似于文献[24]，根据Lyapunov 稳定性理论，可以证明对于所有的i，j=1，2，…，n，i≠j，负载电流分配误差、电压跟踪误差eo以及所有其他闭环系统中的信号都是有界的，在理论上保证了闭环系统的稳定性。

根据式（2）中的变换，可知真实的系统控制输入为：

最后，通过最终得到的控制信号生成PWM波形，来控制电力电子变换器工作[33]。所设计控制器的控制框图如图2 所示。

图2 控制框图

4 仿真分析

通过在MATLAB/Simulink 中搭建的开关级模型，验证所提出控制算法的效果。仿真中采用的控制参数和系统参数分别列于表1 和表2 中。

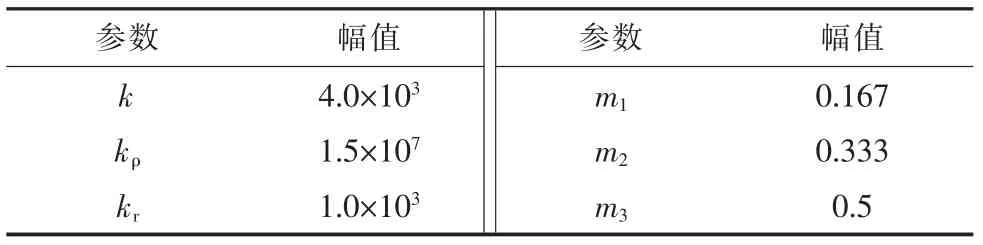
表1 控制参数

表2 系统参数

为了更好地说明所提出的控制算法的有效性，仿真中考虑了负载变化情况，负载1 在0.1s接入，之后在0.2 s，负载2 接入。此外，考虑到真实系统滤波器参数测量的不准确性，仿真中控制器使用的滤波参数和真实参数之间存在±5%的偏差。

母线电压的响应曲线如图3 所示。可以看出，在负载变化的情况下，所设计的控制算法可以保证子系统电压和频率的稳定性。此外，负载电流曲线在图4 中给出。

在图5 中，给出了分布式发电单元输出电流的响应曲线。从图中可以看出，即使在LC 滤波参数不确定以及开关谐波存在的情况下，所设计的算法仍可以保证良好的电流分配，所设计的控制算法具有良好的鲁棒性。

图3 母线电压曲线

图4 负载电流曲线

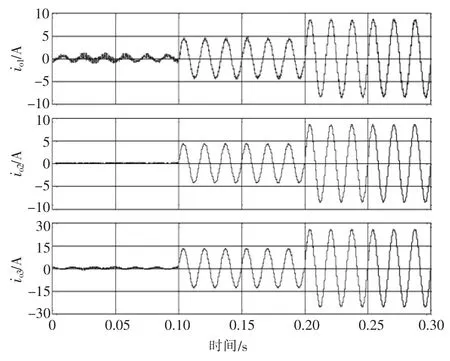
图5 分布式发电单元输出电流

5 结语

本文针对微电网中的并联分布式发电单元，提出了一种分散式控制算法，实现了并联的分布式发电单元之间的按比例负载电流分配，并同时实现了系统母线电压良好的跟踪性能。最后，通过开关级模型仿真，验证了所提出的分散式控制算法的有效性。