基于CFD的轴流式油气混输泵动叶优化设计

马希金，张 耘，刘晓睿

(兰州理工大学能源与动力工程学院，甘肃 兰州 730050)

随着陆地、海洋石油的开发，高气油比油藏在世界油气资源中所占的比例越来越大，油井底部的压力越来越低。由于普通泵和压缩机的工作范围已不能满足高油气比的工况，油气混输泵应运而生。该泵能够从油井中直接采出含有油、气、水及各种杂质的多相混合物并完成集输，大大降低了基建成本，目前已成为各国关注的焦点[1]。本文的研究对象轴流式油气混输泵是一种具有叶片泵和压缩机双重特性的流体机械，其压缩级是由采用锥形结构的动叶和静叶组成。工作时动叶将能量传递给介质，提高介质的动能，静叶则是起到将介质的动能转化为压力能并将两相介质均匀混合的作用，为流体流入下一级动叶做准备。提高混输泵性能的关键在于动叶的设计[2-3]。

兰州理工大学的马希金等[4-6]提出了轴流式油气混输泵动叶的设计方法，并通过数值模拟研究动叶的翼型、进出口角、叶片数、轮毂比和叶栅稠密度对动叶性能的影响。中国石油大学的张金亚等[7]采用数值模拟和实验相结合的方法描述了流道内的流动特性和气泡的分布状况，验证了数值模拟方法在轴流式混输泵性能研究中的可靠性。韩国汉阳大学的Kim等[8]采用2k因子法对叶轮结构进行了优化，提高了动叶的性能。

翼型是动叶建模的基础，我国学者在不变更常规设计方法的基础上，结合自身研究对象特点，对国内外的各种翼型进行了针对性的优化改进。如华中科技大学的游斌等[9]通过改变NACA65翼型前缘形状对常规斜流转子进行前弯设计，有效改善了低流量时轴流式压缩机的旋转失速状态，扩大了喘振裕度和工作范围，减弱了转子下游的尾迹。扬州大学的徐浩然等[10]通过数值模拟研究发现，加厚DU系列翼型后缘厚度，并将厚度控制在弦长5%范围内，能够提高风力机的风能利用效率。由此可见改变前缘和后缘的形状对于翼型的性能有着较大的影响。翼型前缘、后缘的优化设计已经广泛应用于航空航天、风力机、压缩机领域，在油气混输领域还鲜有人研究。

本文以一种典型的螺旋轴流式油气混输泵的动叶为研究对象，在保持轴流转子中弧线和安放角不变的前提下，改变翼型前缘半径大小，采用Pro/E建立单个压缩级的三维实体模型，运用CFD方法对模型进行数值模拟，研究翼型前缘半径对油气混输泵外特性及内部流动规律的影响。

1 叶轮造型和数值模拟

1.1 动叶设计及几何参数

目前国际上关于多相泵的设计理论还不成熟，基于此本文采用升力法对动叶进行设计[11]，设计参数如表1所示。

表1 动叶设计参数

如图1所示，动叶翼型为自主设计的圆头尖尾翼型，翼型厚度变化规律如表2所示[2]。在翼型绕流中，前缘半径R(也称前缘钝度)对流场中的速度、压力分布和分离位置具有显著的影响。为研究翼型前缘半径R值大小对流场的影响，在此引入无量纲参数相对钝度α=R/dmax， 其中R为翼型的前缘半径，dmax为翼型的最大厚度。考虑到动叶头部过大会增大进口处动叶对流体的排挤，且当α取值大于0.4时翼型前缘几乎成为方形，所以α在0.05～0.4之间等间距取值，等间距值为0.05。单级压缩级模型由动叶和静叶串联组成。由于篇幅限制，本文仅对其中比较具有代表性的α取值：0.05(原模型)、0.2、0.3、0.4共4种模型进行探讨，为方便叙述，分别将其命名为M1、M2、M3、M4(如图2所示)。

图1 翼型参数说明

图2 单级压缩级模型

表2 翼型厚度变化规律

1.2 网格划分及无关性验证

由于该泵叶片为空间扭曲叶片，内部流动比较复杂，所以采用适应性较好的非结构化网格[12]。为了更准确地反映泵内真实流动情况，本文为所选取的计算模型适当地向上下游延伸，并对靠近壁面的网格进行加密。网格无关性验证在常温常压纯水工况下进行计算。计算结果表明当整个计算域网格数量达到130万以上时，数值计算所得出的扬程和效率值已不随网格数的增加而变化，此时计算结果趋于稳定。为了提高计算效率，将网格数量控制在130万左右，网格质量在0.4以上，整个增压单元水体的网格划分如图3所示。

图3 混输泵计算区域网格划分

1.3 计算方法及边界条件

数值模拟采用Mixture模型，选择纯水和理想气体作为介质，主相为纯水，第二相为理想气体。假设泵中的气相与液相均匀分布，控制方程为气、液两相的连续性方程和动量方程。

连续性方程：

(1)

动量方程：

(2)

α1+α2=1

(3)

式中：αk为k相体积分数；ρk为k相气相密度；μt为动力黏度；p为压力；uk为k相速度；f为质量力；Mk为k相表面张力。

混输泵工作时叶轮高速旋转，引起内部流场剧烈变化，属于典型的湍流流动，所以选择k-ε模型。在旋流和大曲率面工况下，由于添加了反映主流的时均应变率Eij，RNGk-ε模型比标准k-ε模型精度更高，所以本文数值计算采用RNGk-ε模型。在数值计算中，已假设流体不可压缩，速度-压力耦合采用SIMPLEC算法，离散格式默认为一阶迎风格式，收敛精度设为10-4，进口设定为速度进口，出口为自由出流，叶轮的旋转采用多重参考系，固壁面无滑移[13]。

2 分析与讨论

2.1 动叶压力分布分析

受限于篇幅，本文选取含气率为0.2的工况进行计算分析，分别对设计工况流量Q=100 m3/h和小流量工况Q=60 m3/h进行论述。

图4为Q=100 m3/h，GVF=0.2时4种不同叶片的工作面压力云图。可以看出M4模型叶片压力比其余3种模型相同位置的压力均有所提高，轮毂侧低压区面积明显减小，使得工作面压力分布更为均匀。图5为4种不同叶片的背面压力云图。可以看出叶片背面压力沿弦线方向的分布更加均匀，且M4模型叶片后段的径向压力梯度小于其余3种模型的径向压力梯度，在出口边径向压力梯度逐渐消失。压力梯度过大时会导致径向压力的产生，从而使流动产生漩涡造成二次流损失，所以M4模型能够最大程度地减小能量损失。基于上述分析可得，随着α的增大，叶片工作面和背面的高压区面积都逐渐增大。

图4 Q=100 m3/h，GVF=0.2时叶轮工作面压力云图

图5 Q=100 m3/h，GVF=0.2时叶轮背面压力云图

图6为Q=60 m3/h，GVF=0.2时4种不同叶片的工作面压力云图。可以看出M4模型进口边附近出现了明显的低压区。这是由于在小流量工况下入口速度小于设计流量下的入口速度，造成液流的相对速度与进口安放角不匹配，流体在动叶进口边造成冲击，产生能量损失，从而形成了低压区，这对提高混输泵的性能造成不利影响。随着α的增大，叶片工作面的高压区域面积逐渐增大，且压力场分布更为均匀，这对提高混输泵性能是有利的。图7为Q=60 m3/h，GVF=0.2时4种不同叶片的背面压力云图。可以看出在弦长1/3处靠近轮毂侧形成了明显的低压区，相比前3种模型，M4模型的低压区面积最大，这对提高混输泵性能是不利的。但M4模型叶片背面后半段径向压力梯度相对最小，压力分布较均匀，这对提高混输泵性能是有利的。

图6 Q=60 m3/h，GVF=0.2时动叶工作面压力云图

图7 Q=60 m3/h，GVF=0.2时动叶背面压力云图

2.2 动叶速度分布分析

图8为Q=100 m3/h，GVF=0.2时4种不同模型的动叶子午面速度矢量图，由于动叶进口安放角较小，所以来流会对动叶头部产生冲击。从图中可看出除原模型M1外，其余3种模型在动叶进口边轮缘侧均产生了漩涡，且随着α的增大，漩涡也越明显。这是因为叶片头部厚度随α的增大而增大，使得流道变窄，排挤增大，这对提高混输泵的性能是不利的。在动叶出口位置，动叶出口的流体会对静叶表面产生冲击作用，从而使得靠近动叶出口边轮毂侧的流体流动更加紊乱，更容易形成漩涡。通过对比发现，随着α增大，动叶出口轮毂边的漩涡减小。漩涡减小使得有效过流面积增大，减小了液流的相对速度，从而减小了流动损失，这对提高混输泵性能是有利的。综上所述，增大α能有效改善动叶出口处的流动状况，但在动叶进口处产生小漩涡，对性能的整体影响只能从外特性方面反映。

图9为Q=60 m3/h，GVF=0.2时4种模型的动叶子午面速度矢量图。从图中可以看出，轮缘侧产生了明显的低速区。这是由于流量减小导致液流的相对速度与圆周方向间的夹角变小，而安放角不变，这导致翼型的冲角变大。当流量减小到一定程度时，过大的冲角会导致翼型产生脱流。相比设计工况，进口边和出口边的漩涡更加明显。这是因为小流量工况下，动叶各计算流面产生的增压不等，从而引起了二次回流。二次流通过撞击来传递能量，造成极大的能量损失，降低了水力效率。因此在小流量工况下，混输泵的效率低于设计工况。随着α的增大，动叶进口边轮缘侧的漩涡逐渐增大。在动叶出口边，M1模型形成的漩涡最大，M2、M3、M4模型形成的漩涡大小几乎相等，α对混输泵性能的影响也需要通过外特性来反映。

图8 Q=100 m3/h，GVF=0.2时动叶子午面速度矢量图

图9 Q=60 m3/h，GVF=0.2时动叶子午面速度矢量图

2.3 动叶气相分布分析

图10为Q=100 m3/h，GVF=0.2时动叶流道内子午面的含气率分布云图。从图中可以看出，随着流体从进口流动到出口，密度较大的液体受到较大的离心力被“甩”向轮缘，导致气体多聚集在轮毂侧，形成了大气泡。在两相流中，小直径的气泡基本不与液相发生相对滑移，一旦气泡聚集成为大气泡，大气泡的滑移速度较大，容易加剧气液分离，造成气体聚集堵塞流道现象[14]，所以4种模型在靠近出口边的轮毂侧均形成了高含气区。如图虚线框所示，随着α增大，流道中高含气率区域面积逐渐减小，图中M4模型与M1模型的高含气率与次高含气率区域面积之和的比值约为3:4。在进口边附近， M4模型的含气率也明显低于其他模型，说明较大的翼型前缘半径有利于抑制流体的气液分离，从而改善流道内气体聚集现象。

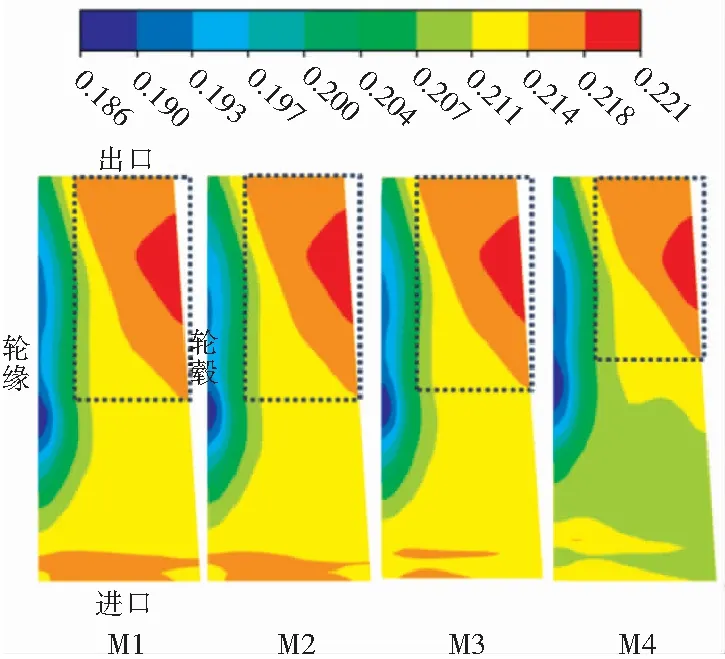
图10 Q=100 m3/h，GVF=0.2时子午面含气率分布图

图11为Q=60 m3/h，GVF=0.2时动叶流道内子午面的含气率分布云图。从图中可以看出，随着α的增大，图中高含气率和次高含气率区域面积之和呈减小趋势，其中M4模型的高含气率区和次高含气率区之和面积最小，图中M4模型与M1模型的高含气率与次高含气率区域面积之和的比值约为4:5，且在轮缘侧含气率也较低。这说明在小流量工况下，M4模型对流体的控制能力较强，能够有效改善流道内气体聚集现象。

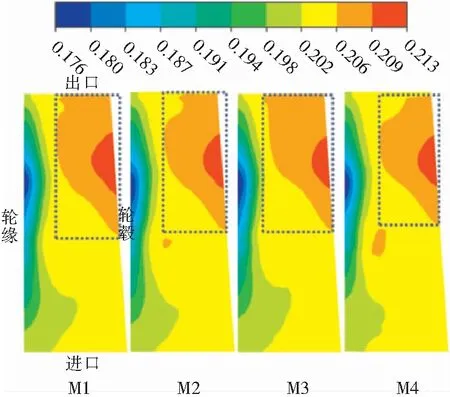
图11 Q=60m3/h，GVF=0.2时子午面含气率分布图

3 外特性预测

为直观描述叶轮增压能力，参照文献[15]，引入以下性能参数。

压缩级增压：

ΔP=Pout-Pin

(4)

压缩级效率：

(5)

式中：Pout为压缩级出口总压， kPa；Pin为压缩级进口总压，kPa；M为泵轴提供的有效转矩，N·m；ω为泵轴旋转的角速度，rad/s。

如图12所示，在设计工况下，该混输泵的增压和效率均高于设计参数，达到了设计目的。在含气率为0.2时，随着流量的增大，4种模型压缩级增压呈现下降趋势，而效率随流量增大呈现先增大，当设计工况Q=100 m3/h时达到最高效率后呈现下降的趋势。

图12 压缩级流量增压效率特性曲线图

如图13所示，在设计工况(Q=100 m3/h)下，M4模型具有更优的性能。以GVF=0.2工况为例，M4模型的压缩级比原模型增压提高了32.6 kPa，效率提高了3.45%。压缩级增压和效率均得到了提高，说明选择合适的翼型前缘半径能够提高动叶的增压能力，以此来提高压缩级的效率。

图13 Q=100 m3/h时不同含气率下压缩级增压效率曲线图

如图14所示，在小流量工况(Q=60 m3/h)下，该混输泵的增压和效率均随α的增大而不断增大，且当设计模型为M4时性能达到最优。从图中可以看出M4模型的压缩级比原模型增压升高了10.98 kPa，效率提高了1.74%。

综上所述，M4模型的性能优于M1模型，达到了优化目的。

图14 Q=60 m3/h时不同含气率下压缩级增压效率曲线图

4 结论

基于RNGk-ε湍流模型及SIMPLEC算法对轴流式油气混输泵不同翼型前缘半径的动叶模型进行了数值分析，分析了不同模型流场中的压力、速度、气相分布规律，得到以下结论。

1)在额定工况(Q=100 m3/h)下，随着翼型前缘半径的增大动叶叶片的压力分布更加均匀。翼型前缘半径较大的动叶模型在出口边附近形成的漩涡尺寸较小，但在进口边由于冲击形成的漩涡较大，外特性计算结果显示利大于弊。流道中的气液分离现象随翼型前缘半径的增大得到了抑制，水力效率得到提高。

2)在小流量工况(Q=60 m3/h)下，随着翼型前缘半径的增大动叶叶片工作面和背面均出现了低压区。翼型前缘半径较大的动叶模型在出口边形成的漩涡较小，但在进口边形成了较大漩涡，外特性计算结果显示利大于弊。较大的翼型前缘半径能够改善流道内的气液分离现象，降低水力损失，提高水力效率。

3)翼型前缘半径为最大厚度40%(即文中的M4方案)时，压缩级的性能提升幅度相对显著。