病原体毒性进化多样性的动力学模型

原博

（山西工程职业学院，山西太原 030009）

生物上现在对于病原体毒性的适应性进化的一个比较合理的解释是病原体毒性与病原体诱导的宿主死亡率之间存在一定的权衡关系，对于这种关系我们没有具体的经验数据，因此我们有必要建立一个具体的模型来研究病原体毒性的适应性进化的机制。利用临界函数分析的方法来研究模型可能出现的进化效果。因此本文考虑宿主的出生率和自然死亡率都不依赖于种群密度的SI模型，利用进化入侵分析的方法研究单同态病原体毒性是否能够产生进化分支，能够产生进化分支前提下进一步是变成两种具有不同毒性的病原体；还是进化到一个连续稳定的策略而停下来。

1 病原体毒力的进化稳定策略分析

1.1 死亡率不具有密度依赖的SI模型

本研究考虑这种由病原体诱发的传染病会造成终身感染（即没有恢复者R），宿主迁入率是常数，所有的新出生个体均为易感者，并且病原体只会水平传播，不会垂直传播（所有新出生个体均是无病的）。其中，S为易感者，I为带有毒性α的病原体感染的感染者，单个感染者感染易感者的传染率是与易感者的种群密度成正比即βS。

SI模型如下：

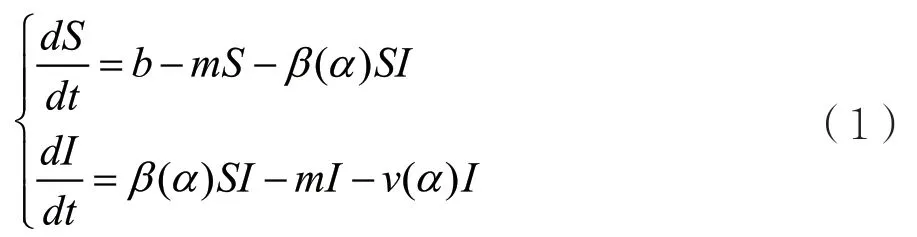
其中，b表示宿主的迁入率，m表示宿主的自然死亡率，v表示带有毒性α的病原体的因病死亡率，β表示与病原体毒性α相关的传染率。当毒性α增加时，相应的将会增加病原体的感染率β，但是同时也增加了因病死亡率v；假设因病死亡率v是毒性α的线性函数，不同的因病死亡率表示具有不同毒性的病原体，反之亦然。因此不失一般性，令v=α，所以β(α)可以看作β(v)。并且注意到传染率是不可能无限增加的，当病原体毒性v很大时，β(v)接近饱和。因此，得到β(v)是关于v的一个单调增加且并具有饱和状态的函数，此时SI模型就简化如下：

其中β'(v)＞0。

当条件

1.2 模型（2）正平衡点的稳定性分析

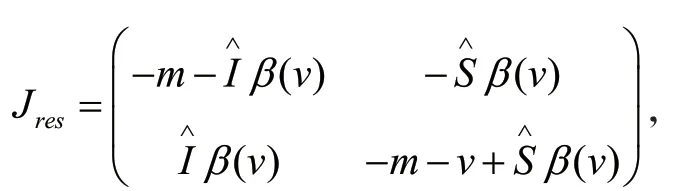
经过计算雅可比矩阵Jres的特征值的实部均为-bβ(v)/2(m+v)。

1.3 突变病原体的入侵适合度

下面推导带有变异病原体的种群动力学模型。当突变很稀少并且突变很小的时候，进一步假设不存在交叉感染的情况（一旦易感者宿主被一种病原体感染以后就不会被另一种病原体感染）。因此，由易感者宿主S，带有毒性v的病原体感染的感染者I，带有突变毒性vm的病原体感染的感染者Im组成的种群动力学模型如下：

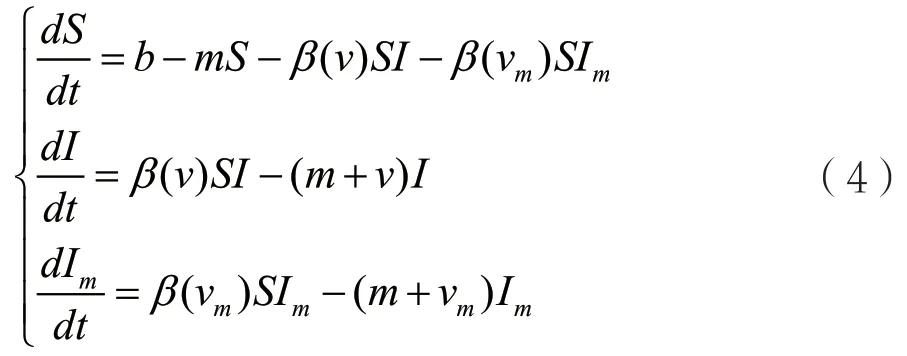
其中，b为宿主的迁入率，m为宿主的自然死亡率，参数vm是变异病原体的因病死亡率，β(vm)为变异病原体相应的传染率。模型（4）隐含的假设就是具有不同毒性的病原体可以对不同的易感者S进行感染，因此两种不同毒性的病原体对于易感者的争夺形成竞争机制。

令Im=0，可以得到没有变异病原体的平衡点：

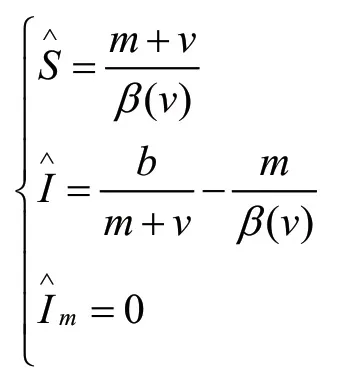
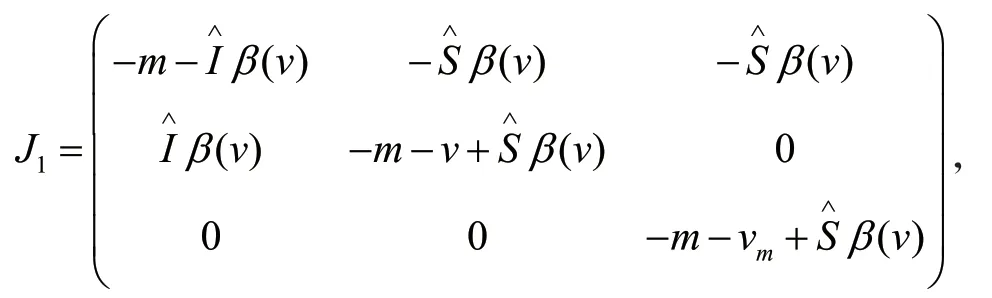
因此当条件

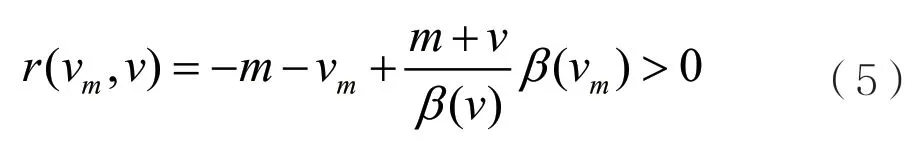
1.4 病原体毒力的进化动力学模型

当突变是稀少的并且突变很小时，通过成功的入侵与替代，病原体的毒性特征将一步一步地进化，并且进化的方向是由局部选择梯度g(v)决定的，其中g(v)如下：

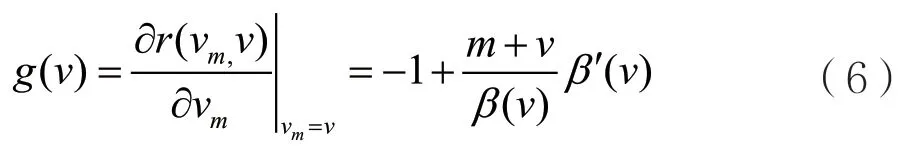
病原体的毒性特征v一步一步的进化过程可以用下面的典型方程去近似。其中典型方程如下：

1.5 病原体毒力的连续稳定策略

当v*满足条件g(v*)=0，时，就称v*为进化奇异策略。

将（7）代入上式，可知v*满足如下条件：

当在进化奇异策略v*处，

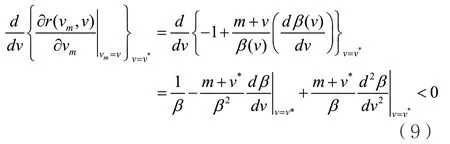
因此可以得到奇异策略v*是收敛稳定的条件如下：

当进化奇异策略v*满足条件

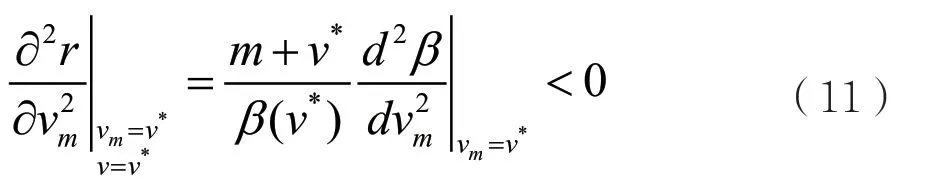
时，那么称此进化奇异策略v*是进化稳定的（ES）。由此，可以得到如下的结论：当条件（3）和（5）满足时，如果权衡函数β(v)在进化奇异策略v*满足β''(v*)＜0，那么进化奇异策略v*既是收敛稳定的，也是进化稳定的。即进化奇异策略v*为连续稳定[3]的进化策略。

由以上分析，可以看到：当权衡函数曲线β(v)是全局凹时，如果进化奇异策略v*是收敛稳定的，那么它必定是进化稳定的。因此进化奇异策略是连续稳定的，不可能产生进化分支。

2 参数对进化奇异策略的影响

2.1 自然死亡率对进化奇异策略影响

接下来研究随着宿主的自然死亡率m的增加，毒性特征v的进化稳定性（ESS）的改变。

假设β(v)满足上面的限制条件即在奇异策略处是凹的，并且是关于v的增函数，因此只要模型中选择的β(v)为饱和函数形式就同时满足上面的两个条件。

进化奇异策略v*必须满足

从（12）可以发现，变异增长率r依赖于参数vm和v。因为vm和v同时在v*处取值，所以方程（12）可以写成：F(v*,m)=0。

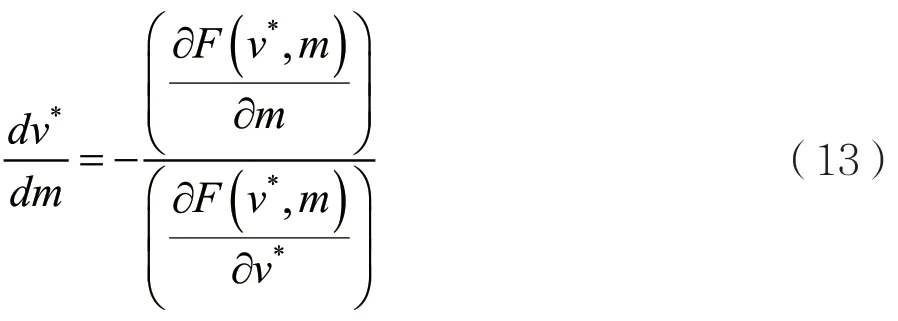
本研究的目标是弄清楚进化奇异策略v*是如何随着参数m的增加而改变的。通过把关于m的隐式微分方程F(v*,m)=0中的v*看作是m的函数[4]，可以得到

通过变形，可以得到

可以利用定义的F(v,m)将（13）写成

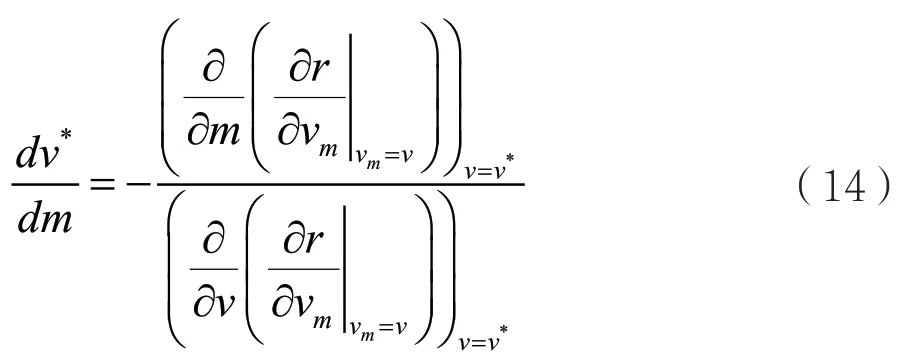
对于进化奇异策略v*来说，假设ESS是连续稳定的，那么方程（14）的分母必定是负的，因此就有：

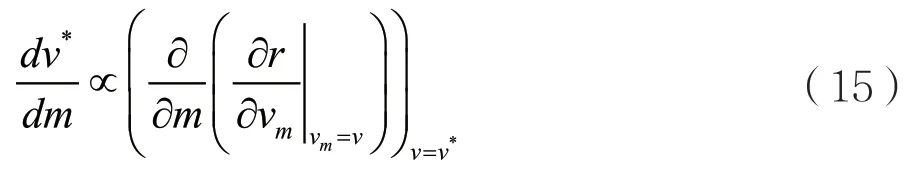
通过条件（11），可以计算方程（15）得到

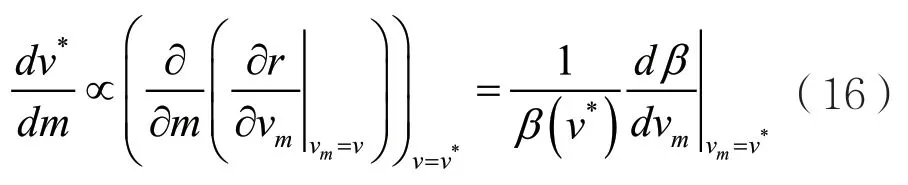
给定的β(v)必定是正的并且在v*处的值是增加的才能出现ESS，此时方程（16）的右边必定是正的，因此对于本模型来说，只要存在收敛稳定的ESS，那么无论β(v)与v的具体关系如何，进化奇异策略的毒性水平v*都必将随着宿主自然死亡率v*的增加而增加。

2.2 出生率对进化奇异策略的影响

通过类似的方法，可以研究进化奇异策略的毒性水平v*随着宿主出生率b的增加是如何变化的[5]。

从图1a可以看出，进化奇异策略v*随着宿主死亡率m的增加而增加，类似的，从图1b可以看出当宿主出生率b增加时，进化奇异策略v*是不变的。还可以发现无论出生率和死亡率如何变化，毒性水平的进化奇异策略v*都不可能出现进化分支的情形[6]。

3 结论

本文研究了病原体毒性的进化多样性，主要分析最初的单同态病原体是否可以通过进化分支产生双同态的病原体，讨论了自然死亡率不具有种群密度依赖的SI模型，研究了模型（1）的进化动力学模型并得出进化奇异策略进化稳定和收敛稳定的条件，发现此模型下只要进化奇异策略是收敛稳定的，就必定是进化稳定的。因此不会出现进化分支的现象。最后讨论了自然死亡率和出生率对毒性特征的进化奇异策略的影响。发现奇异策略v*随着宿主死亡率m的增加而增加，而当宿主出生率v*的增加时，进化奇异策略v*是不变的，还发现无论出生率和死亡率如何变化，毒性水平的进化奇异策略v*都不可能出现进化分支的情形。

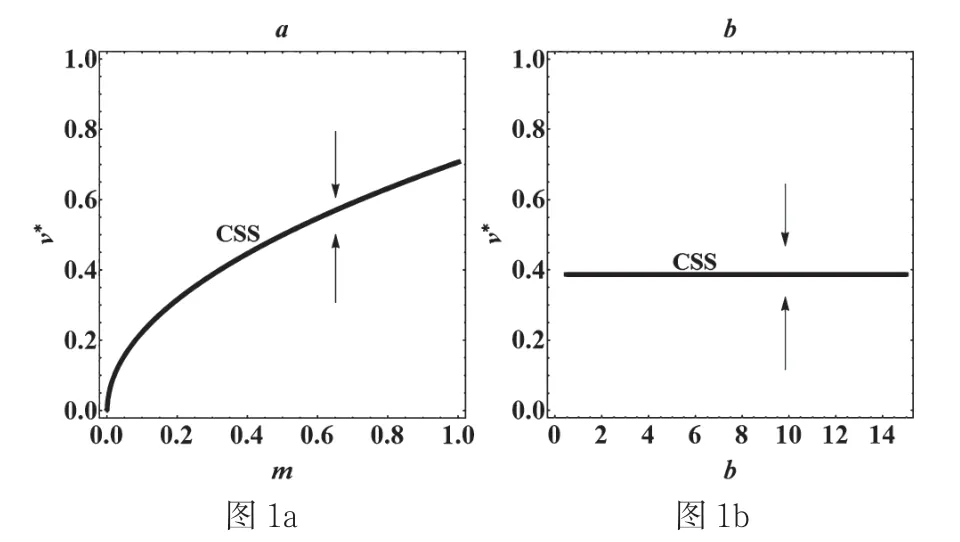
图1 自然死亡率m和出生率b对进化奇异策略的影响