溢洪道明渠扩散段三角翼优化设计数值模拟研究
(辽宁西北发电有限责任公司东源电厂,辽宁 桓仁 117200)
水利水电工程中,扩散过渡段的位置和形态会直接影响到工程的安全运行,必须认真设计和施工[1]。当前,在水利水电工程设计中,为了满足国家和行业标准中关于扩散段扩散角的要求,一般会采取增加过渡段长度的方式。但是,在部分水利水电工程建设中,受坝址区地质以及空间限制,不得不使用较短的扩散段长度,而选择大扩散角过渡[2]。但是,相关学者的理论研究和工程实践也证明,如果扩散段的扩散角过大,边界对水流的影响作用就会显著增强,进而导致水流断面的能量分布不均,导致显著的侧壁回流、边界脱流以及主流偏流等问题,从而影响水工建筑物的正常使用,情况严重的还会危及水工建筑物的安全[3]。由此可见,对于没有足够空间布置小扩散角过渡段的水利水电工程,如何对大扩散角条件下的水流进行控导和干预是亟待解决的工程问题,而这也正是当前水利工程建设领域的薄弱之处,该领域的研究成果也必将具有巨大的理论和实践应用价值。相关工程经验表明,在扩散段设置潜没式三角翼能够对该部位的水体流动起到有效的控制作用,属于比较有效的控导手段,但是如果三角翼设置不合理,仍会产生比较明显的回流区[4]。因此,有必要对三角翼对扩散段的水流控导效果进行深入研究。
1 工程概况
猴山水库位于辽宁省绥中县范家乡赵家甸村境内的狗河上,下游距离绥中县城约35km。该水库的主要任务是城市供水,同时兼具防洪和下游农业灌溉条件改善功能。猴山水库的设计库容为1.6亿m3,工程等别为Ⅱ等。水库的永久性建筑物主要包括大坝、副坝、溢洪道和输水设施。猴山水库溢洪道位于大坝左岸的台地上,其轴线基本与大坝轴线垂直,全长372m,自上游至下游分别划分为导流段、控制段、泄槽段和扩散消能段。
2 计算模型的构建
2.1 几何模型的选择及构建
选择猴山水库工程溢洪道明渠扩散段作为研究原型,考虑本文研究的重点与计算的复杂程度,几何模型选择的是溢洪道扩散段以及上游的直线窄段50m和下游直线宽段120m。
模型创建是流体数值模拟研究的基础和关键环节。结合本次研究对象的实际特点以及相关研究经验,采用AutoCAD三维建模软件进行研究对象的几何建模,利用FLUENT软件进行数值计算模型的构建[5]。一般情况下,模型的网格划分越密集,计算精度越高,但计算量会急剧增大,因此,本文对三角翼部分采用混合网格划分[6],最终获得294110个网格单元,244268个计算节点。
2.2 边界条件
结合本次研究的实际情况以及平面大扩散角衔接过渡段流动数值模拟研究的相关成果,设定如下边界条件:对于模型的入口选取液相速度入口边界条件与气相压力入口边界条件[7]。具体而言,根据模型入口部位的设计流量,计算入口边界均匀来流条件。对于模型的出口,设置压力出口边界条件,根据猴山水库下游的实测水位设置水流自由面的高程,本次研究的模拟工况全部为平面大扩散段两相流问题,模型下游出口处的水流可以自由发展,没有回流现象出现;模型设置为无滑移的固壁边界条件。
3 三角翼数值模拟优化研究方案
3.1 优化研究的关键参数
扩散段三角翼的几何体型特征主要受如下参数控制[8]:ⓐ分流度α,一般情况下该角应设定为单侧扩散角的两倍,同时要保证与来流适应;ⓑ三角翼的潜没度h,增大三角翼的高度有利于提高水流控制能力,但同时会增大水力损失,从而在三角翼的后部产生回流区;ⓒ三角翼的长度,也就是控导度η,该参数主要影响三角翼的控导范围,可以对扩散段的水流流态以及水流动量的调整强度产生显著影响;ⓓ三角翼的攻角,也称攻流度θ,也就是三角翼的翼弦与扩散段来流之间的夹角,其大小可以对匹流和控导效果产生直接影响。此外,三角翼的丰满度b、回流度φ以及位置度λ也是影响三角翼几何体型的重要因素。
3.2 模拟研究方案设计
目前,水利工程研究中三角翼的体型参数优化数值模拟方案并不明确,因此,本次研究基于所提出的主要控制参数,探索三角翼体型优化设计的数值模拟方案,为研究的顺利进行打下良好基础。在工程研究中,控制变量法是针对多因素问题的有效研究方法,理论上,我们可以通过上述方法寻求每个三角翼控制参数的最优值,并最终确定出三角翼体型设计的最佳方案。在具体的研究方案设计中,结合相关研究成果,从方便后期结果分析考虑,仅对控导度、攻流度两个无量纲控制变量进行优化研究,研究方案见表1。

表1 计算方案设计
4 模拟计算结果分析
4.1 攻流度模拟计算结果
利用构建的模型,对不同攻流度条件下的溢洪道扩散段流场进行模拟计算,结果显示:利用a型三角翼体型设计时,水流的流态和整体分布比无控导条件下表现更为稳定,回流区长度明显减小,强度也有所降低。但是在边壁的部分区域产生一定的边界层分离现象,两侧均出现了范围较大的不对称型漩涡,主流位置存在一定程度的偏移,流速的不均匀性仍旧较大。在利用b型三角翼体型设计时,水流的流态和整体分布与a型基本相同,但是两侧漩涡的范围区强度有所增加且中心有向下推移的趋势,下游主流受两侧剪切挤压,摆动不稳定现象比较明显;在利用b型三角翼体型设计时,两侧边壁部位的动量明显增加,边界层分离不复存在,下游主流偏移现象消失,但在翼后方存在范围不大的回流区,使单宽动量不均匀度增大,影响范围也显著增加,呈现出矫枉过正的情况。
为了对扩散段三角翼控导效果进行定量分析,根据模型计算结果绘制出不同计算工况下的各个计算断面的水流单宽动量不均匀度变化曲线(见图1),由图1可知,b型三角翼的控导效果最优,因此,就本次研究的猴山水库溢洪道扩散段而言,攻流度的优化取值为0.75,也就是取67.5°的攻流角。
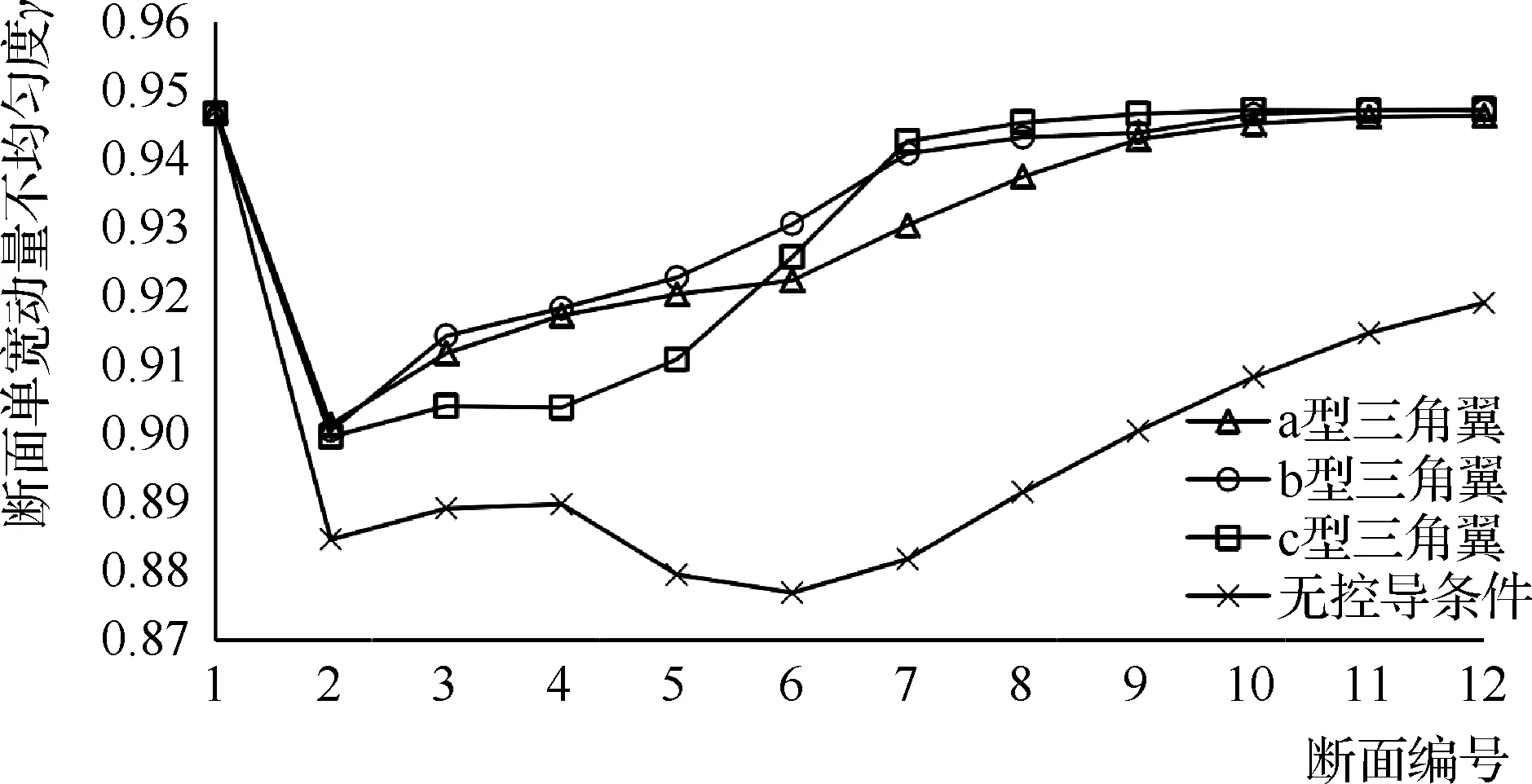
图1 不同攻流度断面单宽动量不均匀度
4.2 控导度模拟计算结果分析
利用构建的模型,对不同控导度条件下的溢洪道扩散段流场进行模拟计算,结果显示:利用d型三角翼体型设计时,扩散段边壁位置不存在明显的边界分离,主流也不存在偏移现象。但是,在三角翼的后方存在一定范围的汇流区,水流流速呈现出两侧大中间小的特征,由于两侧水流速度较大,造成左右激荡作用明显。利用e型三角翼体型设计时,在溢洪道扩散段的左侧存在呈条带状分布的回流区,并且随着三角翼长度的增加,在三角翼的后部和右侧出现了一定范围的弱流区,在一定程度上降低了扩散段的过流能力。
为了对扩散段三角翼控导效果进行定量分析,根据模型计算结果绘制出b、d、e型工况下各个计算断面的水流单宽动量不均匀度变化曲线(见图2),由图2可知,d型三角翼的控导效果最优,因此,就本次研究的猴山水库溢洪道扩散段而言,攻流度的优化取值为0.75,也就是取67.5°,控导度的最优取值为0.40,也就是三角翼的长度为4m,可满足国家和行业标准中关于扩散段扩散角的要求。

图2 不同控导度断面单宽动量不均匀度
5 结 论
本次研究以辽宁省猴山水库溢洪道扩散段为工程背景,利用CFD和FLUENT软件对大扩散角条件下的三角翼优化设计进行数值模拟研究。研究中结合相关研究成果和工程实际,提出扩散段三角翼的几何体型特征的主要控制参数,对控导度、攻流度两个无量纲控制变量进行优化研究。结果显示:针对背景工程,攻流度的优化取值为0.75,也就是取67.5°,控导度的最优取值为0.4,也就是三角翼的长度为4m。

