地磁导航中地磁传感器双噪声联合估计补偿方法

孙 欢，杨宾峰，李 驰，王 润

(空军工程大学信息与导航学院，陕西 西安 710077)

0 引言

地磁导航隐蔽性好，自主性高，抗干扰能力强，能提供全地域，全天候，全天时的导航信息，相比于传统导航方式有着明显优势和更广阔的发展前景[1-6]。

精确的导航离不开对地磁场的精确测量，地磁传感器的观测结果往往受到多种因素的干扰，仪表误差、安装误差、载体内部软硬磁误差及涡流磁场误差都会对观测结果造成不良影响，从而导致较大的定位偏差。因此对于地磁场观测值进行误差补偿，对提高地磁匹配导航的精度有着重要的意义[7-14]。

针对地磁传感器的误差补偿问题，国内外学者进行了诸多研究，V.Renaudin等人在磁场域对各向异性磁阻传感器(Anisotropic Magnetoresistive Sensor，AMR)的校正问题进行了研究，其详细分析了传感器自身仪表误差、软磁以及硬磁误差的来源和产生机理，建模时将这些误差都予以充分考虑[15]。文献[16]采用十二姿态补偿法对地磁传感器进行建模，补偿算法采用了椭圆拟合校准法和神经网络算法；文献[17]对地磁传感器仪表误差、软磁误差进行建模，并通过磁通量补偿来消除磁矩干扰；文献[18—19]对三轴磁力仪测量误差和软硬磁误差进行一体化建模，前者采用椭球拟合校准法进行补偿，后者考虑到观测向量和数据矩阵均存在误差，因此用总体最小二乘进行了补偿；文献[20—22]对三轴磁力仪的仪表误差、安装误差和软硬磁误差进行建模，采用ANSYS、COMSOL Multiphysics等软件仿真建模，并采用最小二乘法进行补偿。

通过分析，以往研究仍存在以下问题：1)模型中普遍没有考虑涡流磁场的影响，对于高速、频繁进行姿态变换的载体，其涡流磁场的影响将会使补偿精度下降；2)以地磁传感器为核心的观测系统性能不稳定会形成系统噪声，该噪声与观测噪声相互耦合会降低观测系统的性能，进而影响补偿精度。本文针对此问题，提出了基于一体化模型的双噪声联合估计补偿方法。

1 误差建模

在磁力仪标定过程中，地磁传感器的三轴x′,y′,z′的非严格正交，将会造成非正交误差CNO，可以表示为：

(1)

在磁力仪安装过程中，原则上传感器坐标系应该与载体坐标系严格一致，但是在安装过程中，将不可避免地出现工差，从而造成安装误差，设磁力仪三轴与载体坐标系三轴的误差角为εx,εy,εz，则安装误差CM为：

(2)

由于制作工艺精度的问题，三轴磁力仪三轴存在细微差异，由此产生刻度因子误差，设三轴的刻度因子误差分别为sx,sy,sz，则刻度因子误差矩阵CSF为：

CSF=diag(sx,sy,sz)

(3)

制作工艺精度和安装工差同样也会造成零刻度漂移误差w和剩磁误差bs，矩阵表达式分别为：

w=[δ1,δ2,δ3]T，bs=[bx1,by1,bz1]T

(4)

硬磁误差是载体内部硬磁材料产生的磁场所造成的误差，记硬磁误差为：

Bh=[bh1,bh2,bh3]T

(5)

软磁误差是软磁性材料被外部磁场激励所产生的误差，外部磁场包括地磁场和载体内部所产生的磁场，可以表示为：

BSI=CSI(H+Bh)

(6)

载体做姿态变换的过程中，将会产生涡流磁场，将其考虑在内，得模型：

B=CH+b+P(ΔB/Δt)+ε

(7)

式(7)中，C=CMCNOCSFCSI，b=CMCNOCSFCSIBh+w+bs，ε为零均值高斯地磁观测噪声，其方差为Σ。

由于观测系统并非绝对稳定，在地磁场观测过程中，将不可避免地产生系统误差，体现在各个系统参量的微小变化，因此地磁场观测模型可以进一步表示为：

B=(C+ΔC)H+(b+Δb)+(P+ΔP)(ΔB/Δt)+ε

(8)

式(8)中ΔC，Δb，ΔP是观测系统不稳定造成的系统参数波动。

2 双噪声联合估计补偿算法

实际观测过程中，除了观测噪声之外，观测系统不可避免地受到各种扰动因素影响，因此不能保证系统参量的绝对精确可信，根据上文式(8)所提模型：

z=B=(C+ΔC)H+(b+Δb)+(P+ΔP)(ΔB/Δt)+ε=f(x,v)+ε

(9)

式(9)中，z为实际观测值，x为真值，v为含扰动的系统参量，其值为v=w+m，w为原始系统参量，m为系统扰动误差，z,x均为3×1维向量，v,w,m为21×1维向量，f(•,•)为非线性观测方程，ε为观测误差，各个量如下所示：

z=[Bx,By,Bz]T，x=[Hx,Hy,Hz]T，

w=[c11,c12,c13,c21,c22,c23,c31,c32,c33,b1,b2,b3,p11,p12,p13,p21,p22,p23,p31,p32,p33]T，

m=[Δc11,Δc12,Δc13,Δc21,Δc22,Δc23,Δc31,

Δc32,Δc33,Δb1,Δb2,Δb3,Δp11,Δp12,Δp13,

Δp21,Δp22,Δp23,Δp31,Δp32,Δp33]T。

以往研究表明，观测误差、系统误差服从零均值高斯分布，且统计独立，令其方差矩阵分别为Q1=E[εεT]，Q2=E[mmT]，其中，Q1为3×3维方差矩阵，Q2为21×21维方差矩阵。

由最小二乘算法原理， 当(z-f(x,w))T·(z-f(x,w))取得最小值时，x取得最优估计值，但当观测方程中含有高斯观测噪声ε时，进行加权处理来抑制噪声的影响，此时，x的最优估计值为：

(9)

鉴于f(•,•)的非线性特征，在解算过程中将进行迭代求解。在认为系统参量w精确可信(观测量误差仅由观测噪声产生)的情况下，经常采用基于一阶Taylor展开的数值迭代算法，也称为Gauss-Newton迭代法，其原理是对f(•,•)作线性近似，每一次的迭代值作为下一次迭代的更新公式，重复此过程直至收敛。

(10)

则k-1次迭代结果可通过如下线性加权最小二乘器获得，如式(11)所示。

由于该问题是关于x的二次优化问题，因此存在闭合最优解，其值如式(12)所示。

这同样是关于x和w的二次优化问题，因此存在闭合解，如式(16)所示。

(11)

(12)

(13)

(14)

(15)

(16)

(17)

3 模拟仿真与实验验证

3.1 模拟仿真

利用仿真数据对上述算法进行验证，根据上文所述地磁场观测值模型，设地磁场真实值为50 000 nT，相关参量取值如下：

产生仿真数据时，观测噪声、系统噪声服从均值为0，方差分别为50和30的高斯分布。

首先，不加噪声产生地磁场观测数据，分别采用含涡流磁场模型和不含涡流磁场模型进行补偿，补偿结果如图1所示。

图1 不同模型补偿效果Fig.1 Different model compensation effects

由图可知，含涡流磁场模型在地磁场补偿中，不仅能够显著降低误差峰值，而且可以有效滤除载体姿态转动所引起的波动干扰，具有更高的补偿精度和稳定性。由此确定了含涡流磁场模型的优越性。

其次验证Gauss-Newton迭代法在无系统噪声时的可用性，此时仿真数据不含系统噪声(即系统参量真实可信)。在补偿过程中，相应的观测噪声标准差设为σ=100δ nT，其中δ为观测量扰动参数(数值从1到29变化)，地磁场解算值的均方根误差随观测量扰动参数变化如图2所示，整体补偿效果如图3所示。

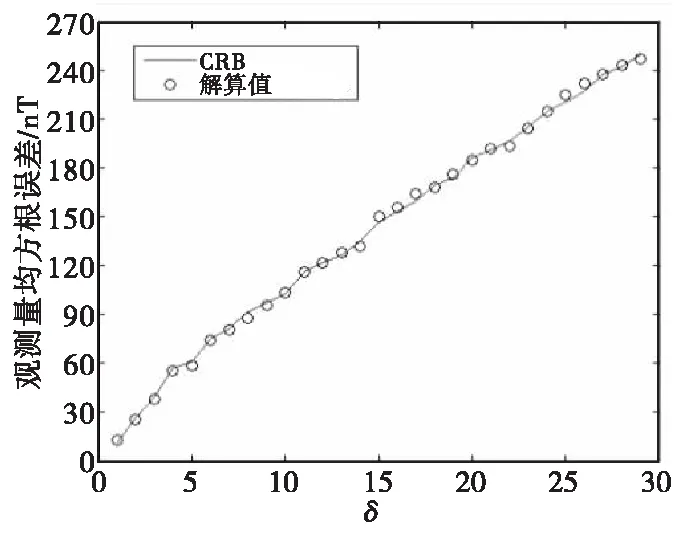
图2 地磁场解算值的均方根误差随δ变化Fig.2 The root mean square error of the geomagnetic field solution value changes with δ

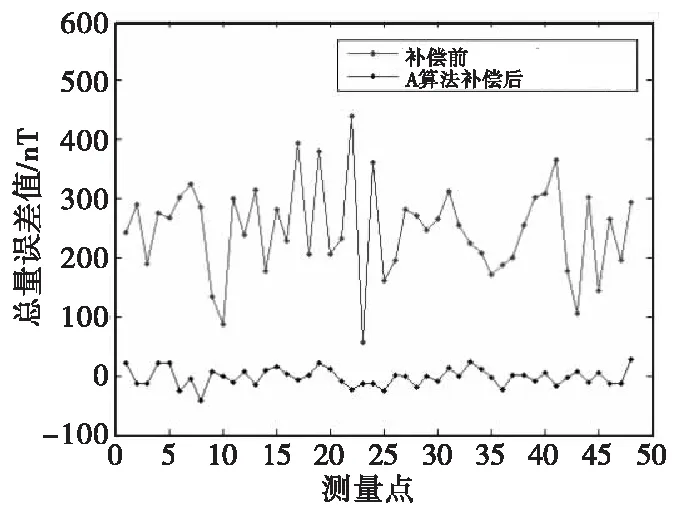
图3 地磁场补偿效果(不含系统噪声)Fig.3 Geomagnetic field compensation effect (without system noise)

由图2和图3可知，解算值的均方根误差可以达到相应的Gramer-Rao界(CRB)，在补偿中将峰值误差从400 nT降至30 nT，证明Gauss-Newton迭代法在系统噪声不存在的地磁场补偿中完全可用。

当仿真数据中加入系统噪声以后，分别以基于Gauss-Newton迭代法(A算法)和Taylor-B迭代法(B算法)的加权最小二乘算法进行补偿，设相应的观测噪声标准差为σ=100δnT，系统噪声标准差为υ=30εnT,其中，δ和ε为观测量扰动参数(数值从1到29变化)，则地磁场解算值的均方根误差随δ和ε变化如图4和5所示，整体补偿效果如图6所示。

由图4和图5可知，当系统噪声存在时，基于Gauss-Newton迭代法的加权最小二乘解算值的均方根误差远远高于相应的CRB，已经不适用于误差补偿；而基于Taylor-B迭代法的加权最小二乘解算值均方根误差达到了相应的CRB，理论上可以进行补偿；由图6可知，在对仿真数据的补偿中，基于Gauss-Newton迭代法的加权最小二乘将峰值误差从700 nT降至400 nT，仍达不到期望精度，而基于Taylor-B迭代法的加权最小二乘由于去除了系统噪声带来的误差，将峰值误差降至20 nT，进一步提高了补偿精度，使得地磁场观测值补偿有了更好的适用性。

图4 地磁场解算值的均方根误差随δ变化Fig.4 The root mean square error of the geomagnetic field solution value changes withδ

图5 地磁场解算值的均方根误差随ε变化Fig.5 The root mean square error of the geomagnetic field solution value changes with ε

图6 地磁场补偿效果(含系统噪声)Fig.6 Geomagnetic field compensation effect (with system noise)

3.2 实验设计

在设计实验中，采用一款Bartington公司的Mag-03地磁传感器进行补偿，为模拟飞行载体姿态变化，选用3FHT30C无磁转台提供姿态信息，数据采集软件用National Instruments，如图7所示，后期用Matlab进行数据处理。地磁场真实值由标准磁图提供。

选取远离强磁干扰的实验场所，将地磁传感器置于无磁转台，快速旋转进行全方位姿态信息测量。为保证测量噪声拟合高斯分布，测量10组数据并选取相同姿态的数据作为实验数据，系统参量初值选用经验值(先验值的不准确度即为系统噪声)。将软件采集数据用本文所提两种算法进行处理，所得结果如图8所示，未经补偿的地磁场测量值峰值误差可达3 000 nT，基于Gauss-Newton迭代法的加权最小二乘算法有着一定的补偿效果，将误差峰值降至1 600 nT，但仍然达不到地磁导航精度要求，基于Taylor-B迭代法的加权最小二乘算法由于滤除了系统噪声带来的干扰，将峰值误差降至90 nT，因此实现了更高精度的补偿，证明了所提算法的正确性和实用性。

图7 实验装置Fig. 7 Experimental device

图8 实际补偿效果Fig. 8 Actual compensation effect

4 结论

本文提出了地磁导航中采用一体化模型的地磁传感器双噪声联合估计补偿方法。该方法有效抑制了涡流磁场和双噪声带来的不良影响，提高了地磁传感器补偿稳定度和补偿精度。仿真和实验结果表明，采用一体化模型的双噪声联合估计补偿方法补偿结果波动明显减小，且补偿精度提高一个数量级，具有一定的工程应用价值。