有源电力滤波器半矢量预测控制策略研究

龚静，张巧杰

有源电力滤波器半矢量预测控制策略研究

龚静，张巧杰

（北京信息科技大学自动化学院，北京市 海淀区 100192）

针对经典模型预测电流控制算法电压矢量选择范围有限、电流跟踪精度不高的问题，提出改进型模型预测电压控制算法。利用滚动寻优得到较优电压矢量，再利用较优电压矢量和零矢量各作用s/2得到半幅值矢量，根据较优电压矢量和半幅值矢量的评价函数选择最优电压矢量。每个周期仅增加一个电压矢量，能有效减小预测电压矢量和实际电压矢量之间的误差，实现对谐波电流的准确跟踪，提高有源电力滤波器的补偿性能。仿真结果表明，所提出的改进型模型预测电压控制算法与经典模型预测电流控制算法相比，补偿电流对参考电流的跟踪更加准确，经补偿后并网电流中的谐波含量由4.86%下降到3.32%，且在稳态和动态情况下都能实现单位功率因数并网。

模型预测控制；有源电力滤波器；电流谐波；最优电压矢量

0 引言

在电力电子领域中，各种非线性负载及不平衡电网造成了严重的谐波污染，致使电网电能质量变差。有源电力滤波器(active power filter，APF)作为改善电网电能质量的一个重要补偿装置，具有较快的响应速度和较好的响应精度，其控制策略引起了广泛的讨论与研究[1-4]。

随着处理器性能的不断提高，模型预测控 制(model predictive control，MPC)[5-6]近年来被广泛应用到不同的控制对象上，且取得了较好的控制效果[7-13]。文献[14-16]提出了两电平电压源逆变器的有限控制集模型预测控制策略，其控制效果优于PWM调制方法，该模型预测控制算法只能在1个零矢量和6个非零矢量中选择最优电压矢量输出，有效矢量的选择范围有限；文献[17]提出广义双矢量的概念，通过评价函数优化2个矢量在一个采样周期内的作用时间获得广义双矢量，共有28种两两电压矢量组合，扩大了有效电压矢量的选择范围，减小了电流脉动，但是每个采样周期均需要进行28次遍历寻优，计算量较大；文献[18]提出利用2个相邻电压矢量合成1个方向可调的虚拟电压矢量，6个虚拟电压矢量的加入扩大了备选电压矢量的方向，减小了预测误差，但其计算较为复杂，动态补偿效果不佳；文献[19]提出由6个有效矢量合成15个虚拟矢量，在21种矢量组合方式中选择一种合适的方式用于调制，提高了负载的电流性能，但开关频率与开关损耗较大。针对以上问题，本文提出一种基于半矢量的改进型模型预测电压控制(model predictive voltage control，MPVC) 算法，以三相三线制APF为控制对象，采用基于瞬时无功功率理论的i-i电流检测法获取非线性负载的谐波电流，预测模型的被控量为APF的输出电压，以预测电压矢量和实际电压矢量的方差构建评价函数，半幅值矢量由有效矢量和零矢量各作用s/2获得，在每一个采样周期选择出较优电压矢量的基础上再次计算对应半幅值矢量的评价函数，每个周期仅增加一个电压矢量。仿真结果表明改进型模型预测电压控制算法能有效降低并网电流的谐波含量，符合并网要求，APF在稳态和动态情况下都对非线性负载产生的谐波电流具有良好的补偿效果。

1 有源电力滤波器的数学模型

图1为三相三线制APF的拓扑结构，Load为所带负载，a、b、c为理想三相电网电压源，a、b、c为APF输出的补偿电流，输出经L型滤波器接入电网，其中为滤波器L的内部阻抗，dc为直流母线电压。

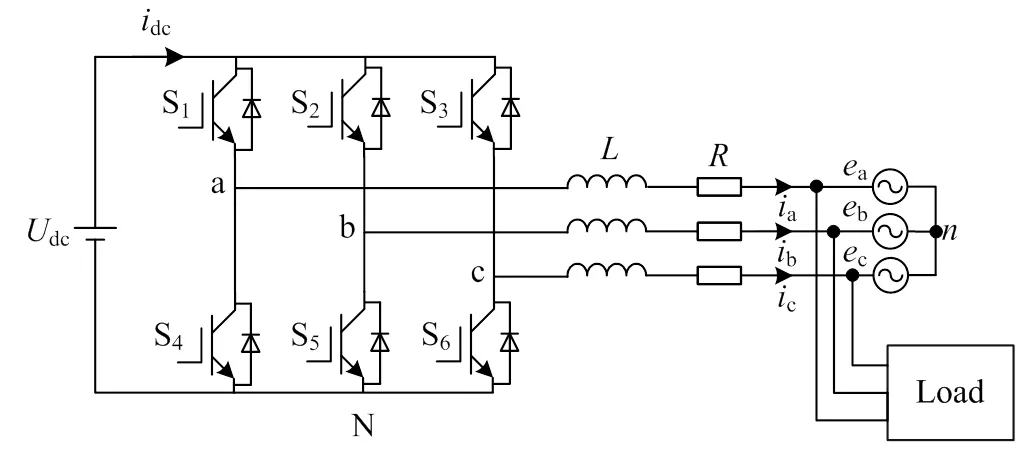
图1 APF变流器拓扑结构图

三相三线制APF由6个开关管组成，分别位于每一相的上下桥臂。为避免发生短路，对于每一相桥臂，每一个时刻只允许一个开关管导通。将各桥臂的开关函数定义为

其中=a，b，c。

APF输出电压矢量和开关状态矢量的关系为

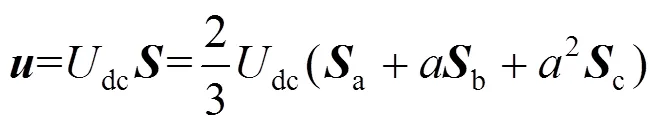
式中=e2p/3。

将所有可能的开关状态组合，得到8种电压矢量，其中0=7在复平面内产生如图2所示的7个电压矢量。

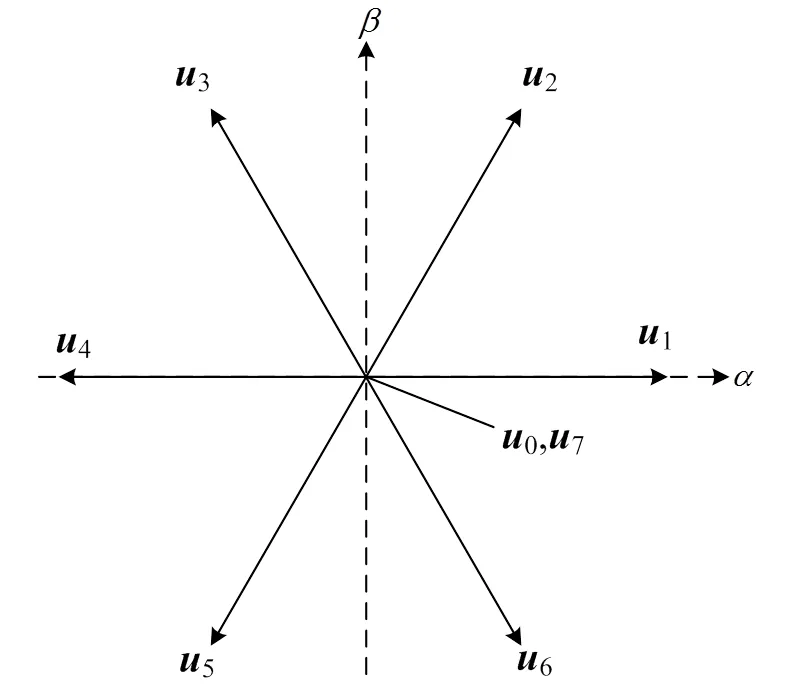
图2 复平面的电压矢量

假设三相电网电压平衡，根据KVL定律得到电压的关系为

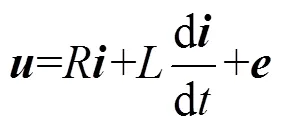
2 改进型模型预测电压控制算法

2.1 模型预测控制的基本原理

模型预测控制是一种基于模型的闭环优化控制策略，其算法的核心是通过预测模型利用控制量计算每一种开关状态下被控量的值，再根据评价函数选择最接近参考值所对应的开关状态作用于变流器。其基本原理如图3所示，首先通过谐波得到参考值x*(t)，根据tk时刻的x(tk)及系统的预测模型得到不同控制信号S1-S7在tk+1时刻对应的预测值，根据预测值和参考值的评价函数选择使评价函数最优的控制信号S3作为tk+1时刻的控制信号，使输出量更接近参考量，下一时刻以同样的方式选择控制信号。

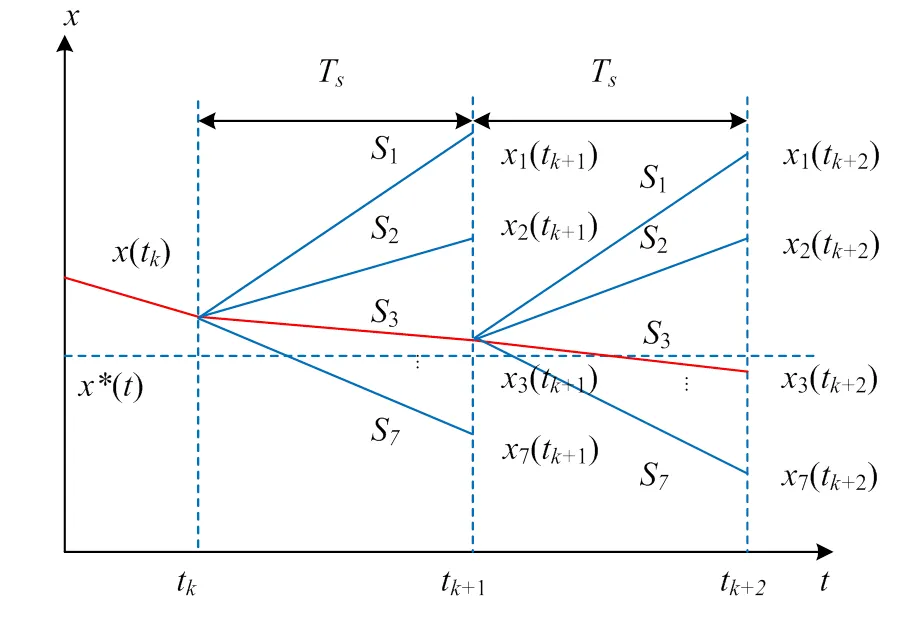
图3 MPC基本原理

2.2 预测模型的离散化

由Clark坐标变换得到式(3)在坐标系下的表达式：

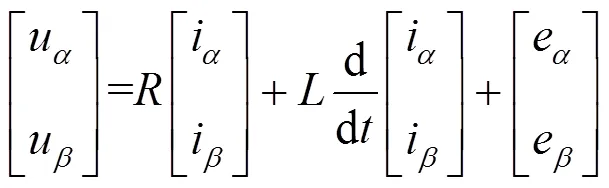
设信号采样周期为s，使用前向欧拉逼近电流导数，将式(4)离散并化简得到APF产生的电压矢量值在+1时刻的电流值：

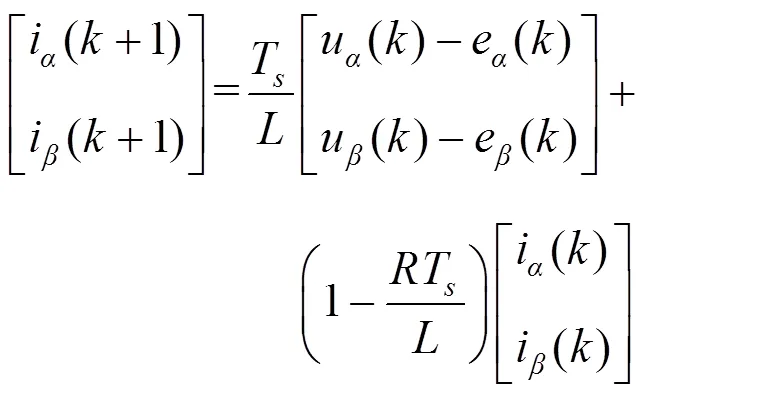
式(5)为被控量为电流时的预测模型，将对电流的控制转换为对APF输出电压的控制，对式(5)进行恒等变换有：

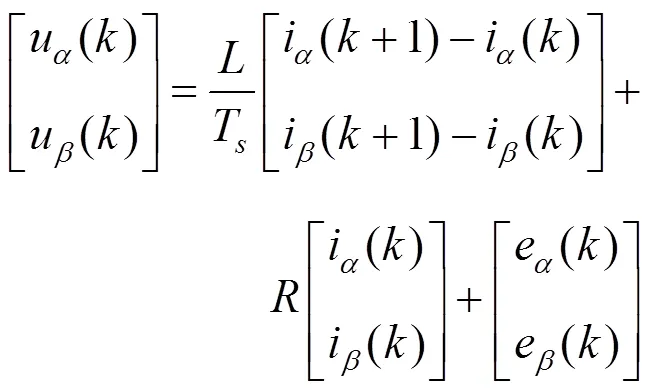
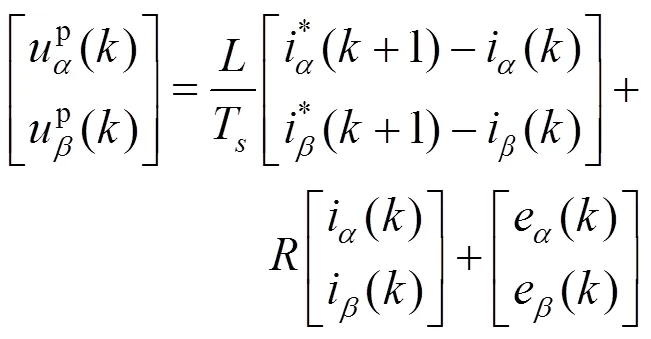
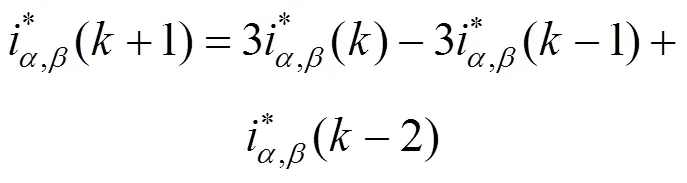
2.3 评价函数的构造

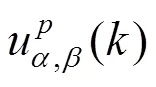
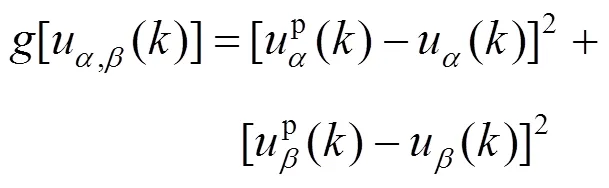
2.4 改进型MPVC的算法实现

经典的FCS-MPC只有7个基本电压矢量，电压矢量的选择范围十分有限，为了得到与预测电压矢量误差更小的电压矢量，通过增加每个有效电压矢量的半幅值电压矢量(简称为半矢量)，更好地逼近预测电压矢量，从而获得更精确的补偿电流，改善APF的补偿性能。半矢量由非零矢量与零矢量分别作用s/2合成，半矢量与对应非零矢量的关系如图4所示。通过遍历寻优法获得较优电压矢量后，再比较该较优电压矢量及其对应半矢量的评价函数，选择与预测电压矢量误差最小的电压矢量作为最优电压矢量输出。对比于MPCC，该改进型MPVC只增加一个选择最优电压矢量的计算步骤，能控制APF获得更准确的补偿电流，提高并网电流的质量。

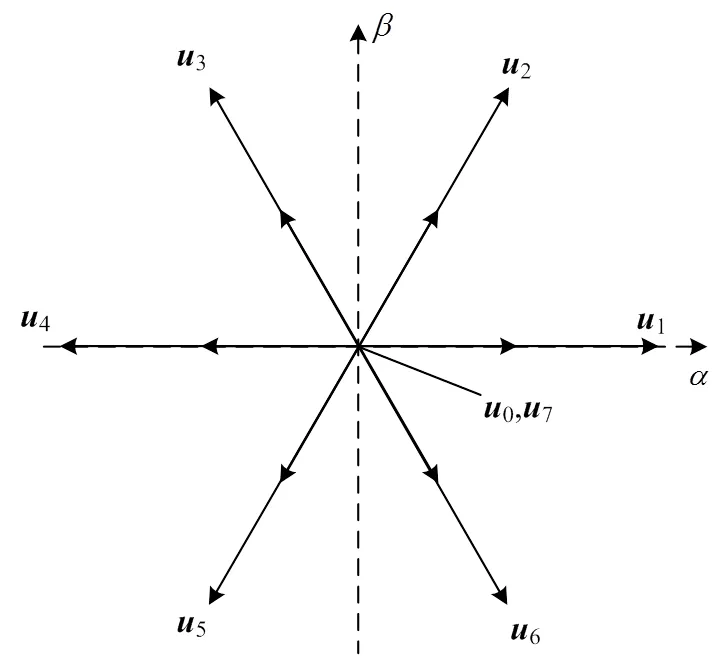
图4 基本矢量与半幅值矢量的关系

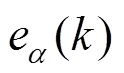
3 仿真分析

3.1 仿真参数设置

为了研究有源电力滤波器补偿负载电流谐波的效果，验证基于半矢量的改进型模型预测电压控制算法与经典模型预测电流控制算法的有效性以及所提算法的优越性，在Matlab/Simulink仿真软件中搭建仿真模型进行验证，仿真参数见表1。

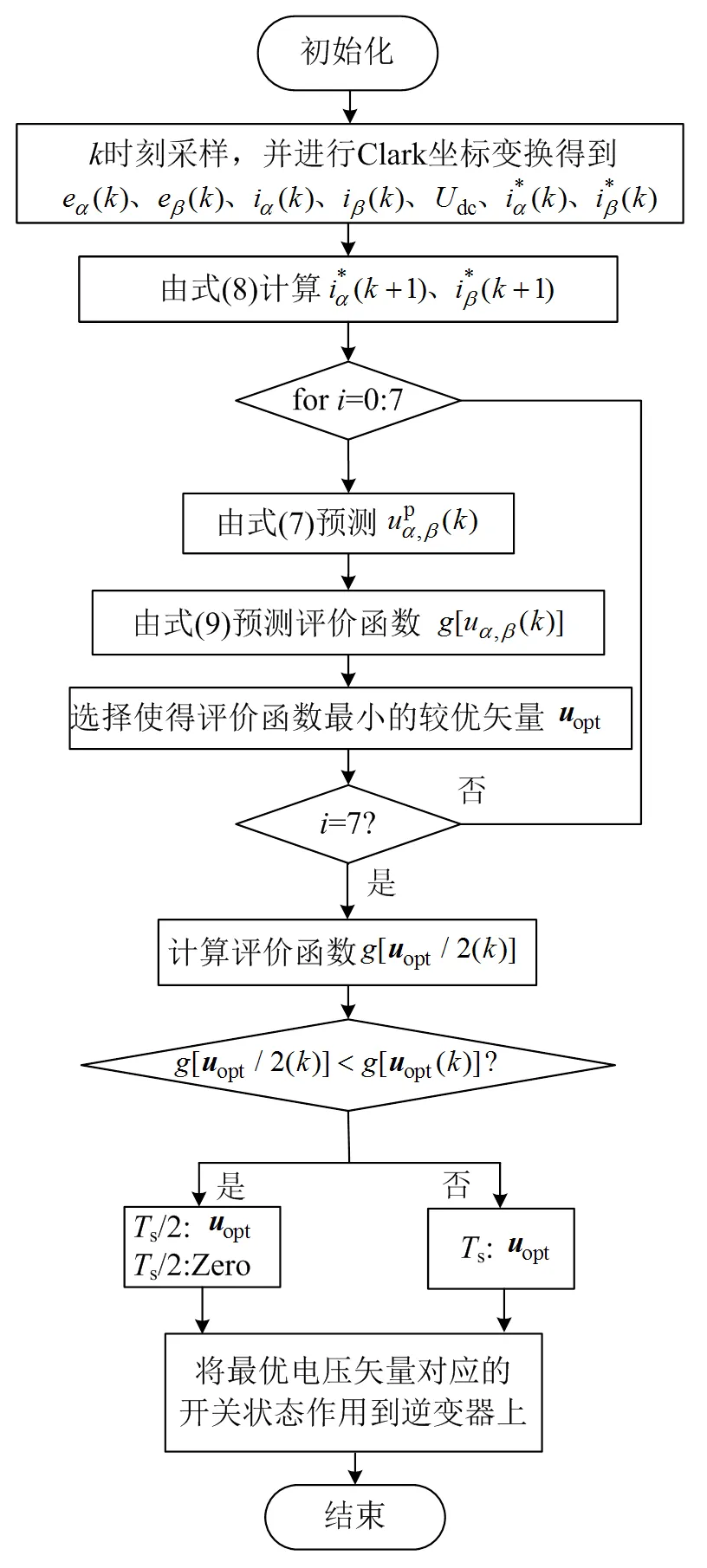
图5 改进型MPVC算法流程图

表1 仿真参数

3.2 稳态效果分析

用三相二极管全桥式不可控整流电路模拟非线性负载，向理想三相电网注入谐波电流，整流桥的直流侧带阻感性负载，其中L=10W，L=5 mH，如图6所示。

使用基于瞬时无功功率理论的ii谐波电流检测法从负载电流中分离出基波电流和谐波电流，如图7所示。由于系统三相对称，本节分析均以A相为例，由上至下依次是负载电流La、分离出的基波电流fa、APF所需要补偿的谐波电流ha，利用快速傅里叶变换(fast Fourier transform，FFT)工具对负载电流进行谐波分析可知，负载电流的总谐波含量(THD)高达26.29%，如图8所示。

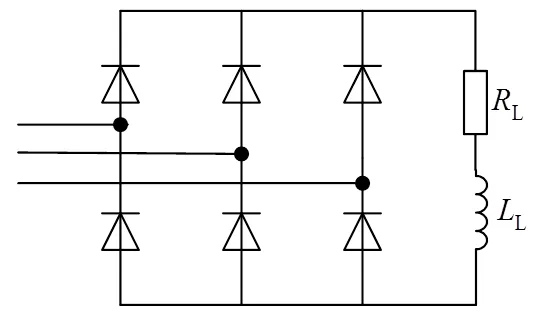
图6 二极管整流桥负载

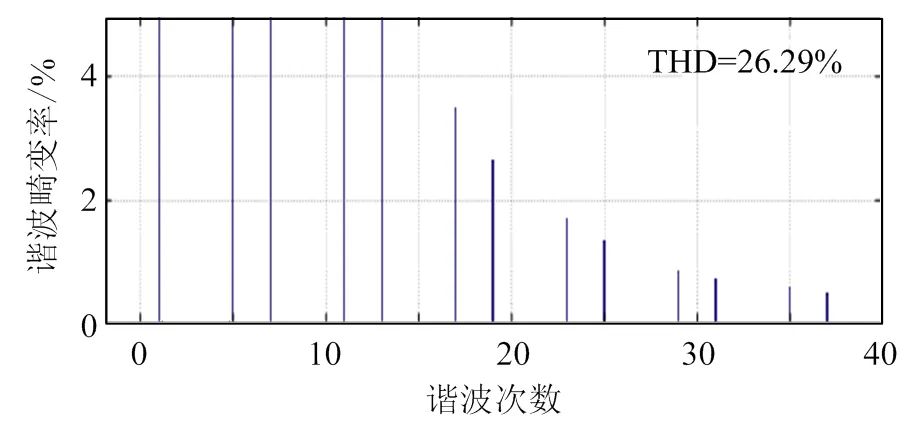
图8 负载A相电流FFT分析

分别使用经典MPCC策略和改进型MPVC策略对APF进行控制，图9为并网电流波形对比，由图9可知，使用改进型MPVC补偿后的并网电流纹波有所减小，较经典MPCC补偿后的并网电流波形更加平滑。图10为补偿电流对参考电流的跟踪对比，由图10可知，使用改进型MPVC产生的补偿电流更精确，与参考电流的误差更小，对谐波电流的补偿效果更好。图11为并网功率因数对比，由图11可知，使用改进型MPVC后的并网功率因数在1附近的波动较小，能准确实现单位功率因数并网。图12为补偿后并网电流中的谐波含量对比，由图12可知，使用改进型MPVC控制的APF对谐波电流的补偿效果更佳，谐波含量由补偿前的26.29%下降至3.32%，低于使用经典MPCC控制方法补偿后的谐波含量。

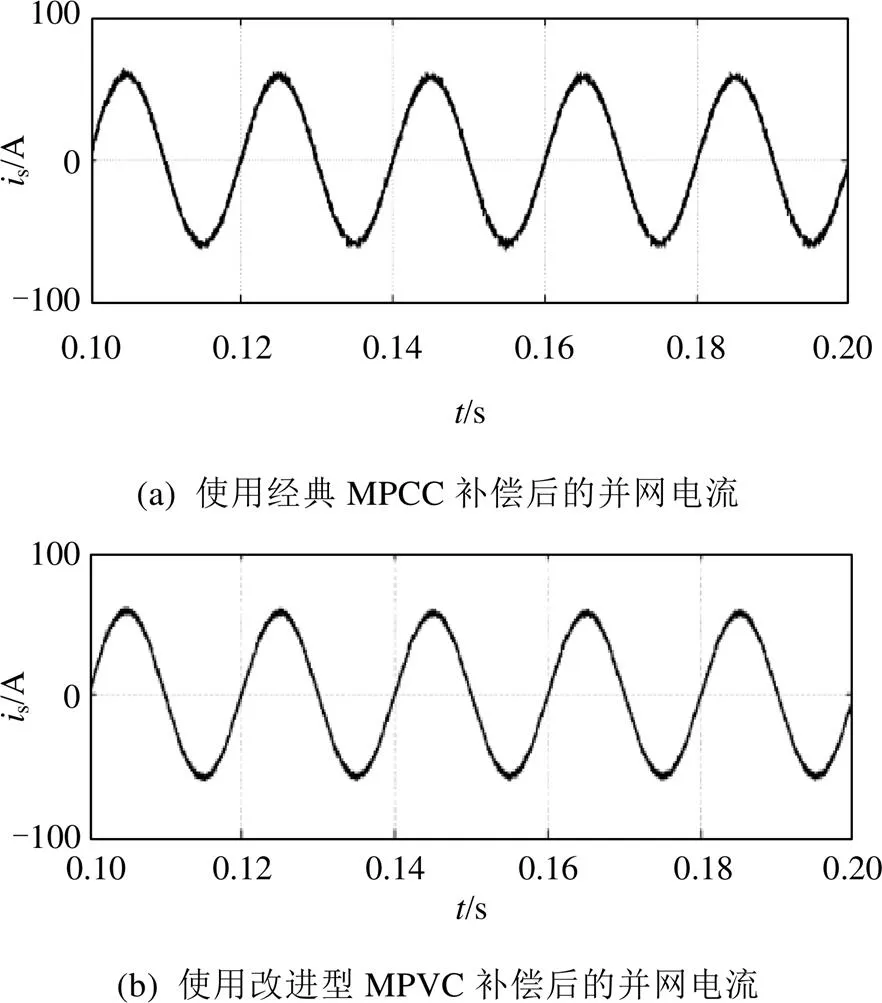
图9 使用2种方法补偿后的并网电流波形对比

3.3 负载突变实验

为了分析APF在非线性负载突变时的运行情况，验证有源电力滤波器的抗干扰能力，进行负载突变实验。设置参数为L1=10W，L1=5 mH，L2=5W，L2=5 mH，仿真总时长为0.4 s。将直流侧只有L1接入的整流桥作为非线性负载的初始状态，在0.2 s时，将负载L2接入整流桥，模拟负载突增；0.3s时，断开负载L2，负载恢复初始状态，模拟负载突降。如图13、14所示，在负载突增的瞬间，经APF补偿后的并网电流能够快速响应，同时APF产生的补偿电流能快速响应参考电流的变化，在0.2s和0.3s负载发生突变时能稳定跟踪参考电流幅值。如图15、16所示，在负载发生波动时，电网电压和电网电流仍能保持同频同相，功率因数在0.2s及0.3s时在1附近发生轻微波动，仍维持在1附近，证明所提算法具有较好的鲁棒性。

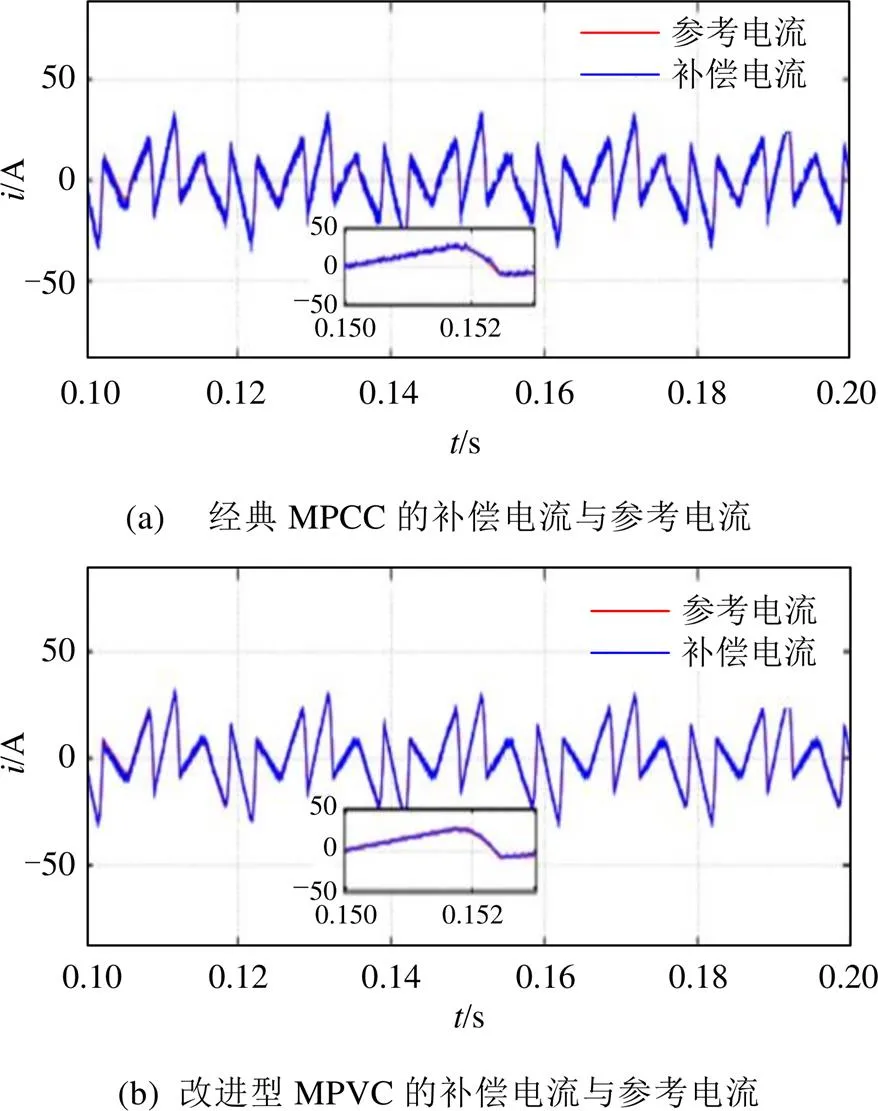
图10 使用2种方法的补偿电流与参考电流对比图

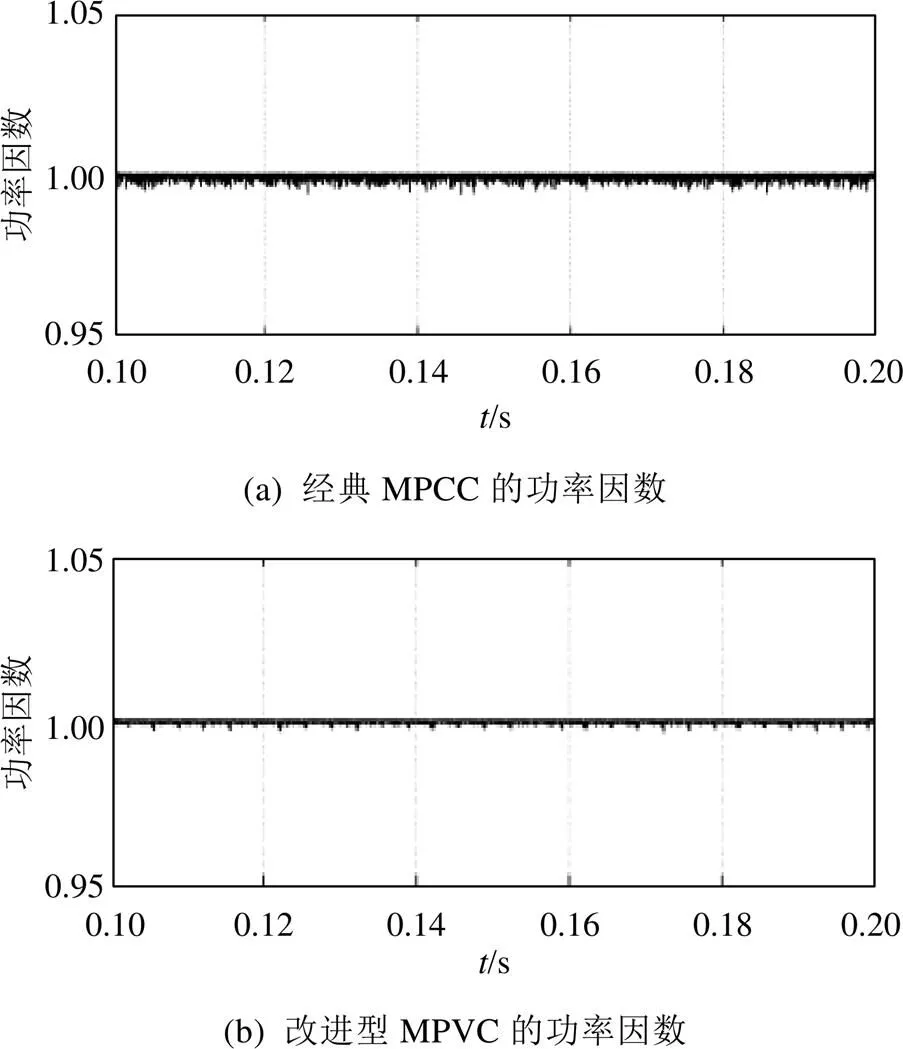
图11 2种方法的功率因数对比

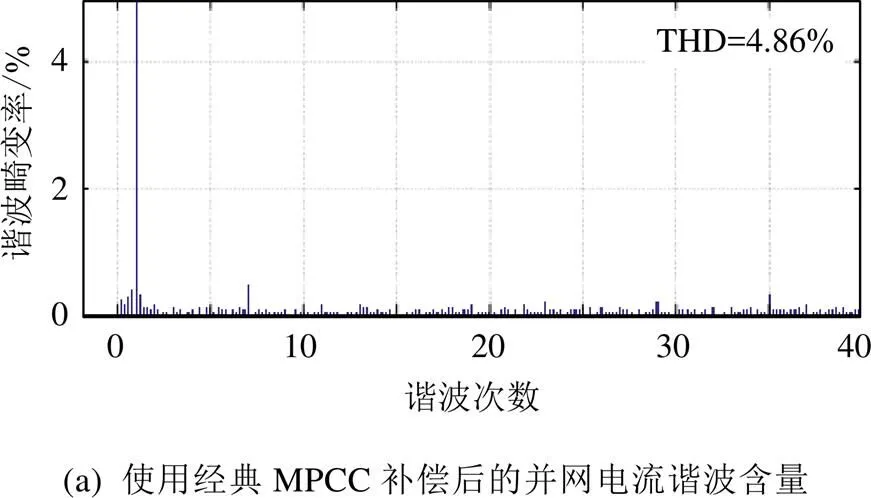
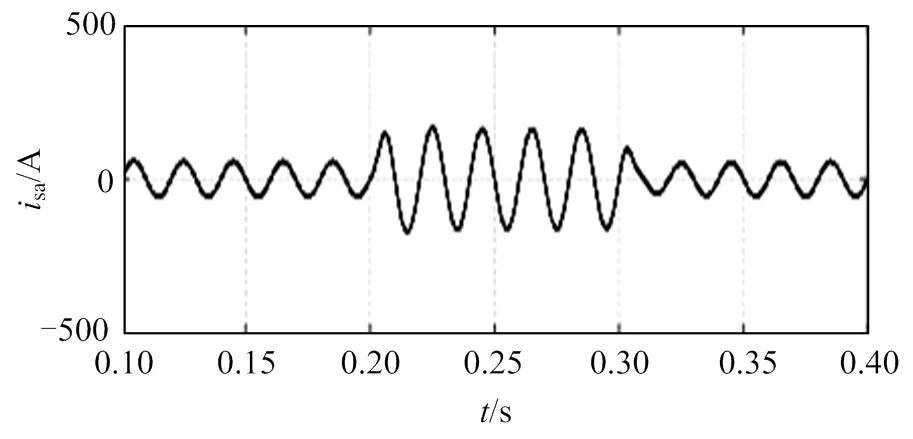
图13 负载波动时的A相并网电流

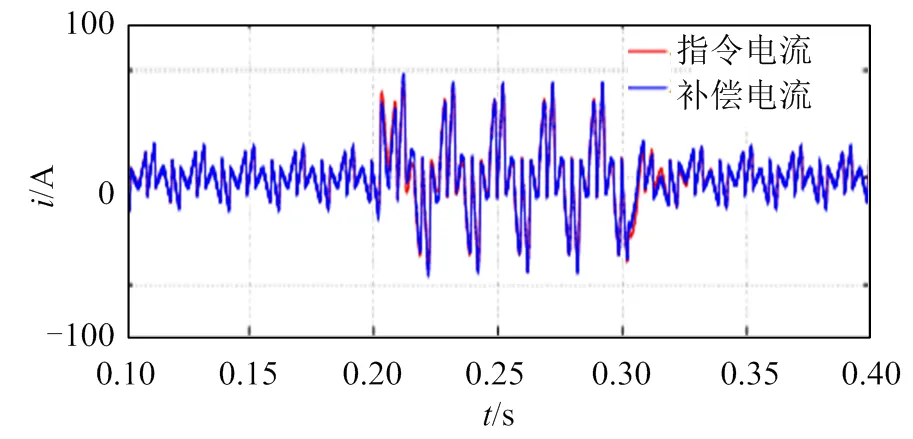
图14 负载波动时的补偿电流与参考电流

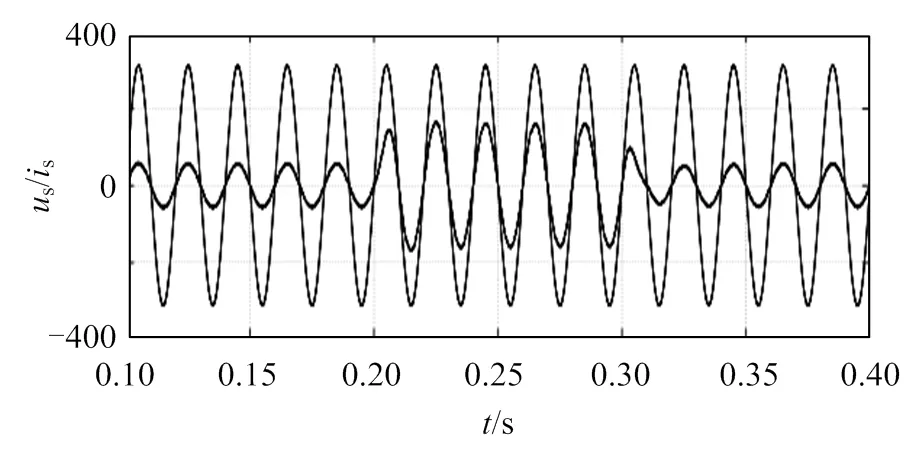
图15 负载波动时的并网电压/电流曲线

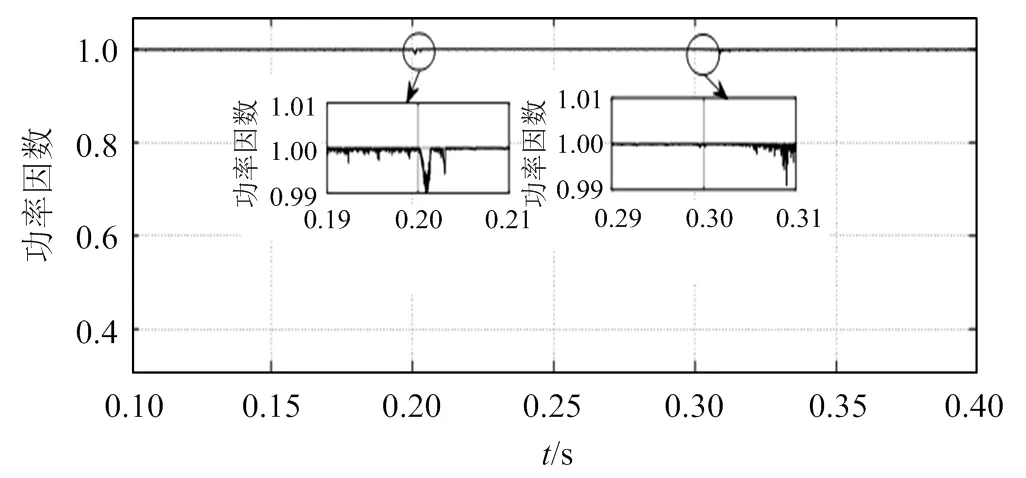
图16 负载波动时的功率因数曲线

4 结论

经典的模型预测电流控制方法由于可选矢量的有限性导致对谐波电流的补偿精度不够，提出的改进型模型预测电压控制算法在每一个采样周期仅增加一个电压矢量，在选定较优电压矢量的基础上，进一步评估其半幅值矢量的评价函数，再次选择最优电压矢量，使补偿的谐波电流更接近参考电流，提高APF的补偿精度。仿真结果表明，改进型模型预测电压控制算法保留了不需调制器的优点，提高了稳态性能，维持了良好的动态性能。

[1] 何蔓蔓，马龙华．三相电压型逆变器的模型预测控制[J]．电气自动化，2016，38(5)：1-3．

[2] 程启明，王玉娇，程尹曼，等．基于并联型有源电力滤波器的无源控制方法[J]．广东电力，2019，32(4)：10-16．

[3] 赵国生，赵丹．三相四线制有源电力滤波器多目标优化预测控制策略研究[J]．电力系统保护与控制，2017，45(17)：1-6．

[4] 林松霖．并联有源电力滤波器谐波检测与控制策略研究[D]．天津：天津理工大学，2016．

[5] 模型预测控制：现状与挑战[J]．自动化学报，2013，39(3)：222-236．

[6] 杜剑行，朱冬雪．基于模型预测控制的风电场多层级无功电压优化[J]．电力科学与工程，2017，33(9)：44-50．

[7] 柏睿，王辉，李晟．基于模型预测的双PWM的一体化协调控制[J]．电力科学与工程，2019，35(4)：45-50．

[8] 郭磊磊，金楠，申永鹏．一种基于优化电压矢量选择的电压源逆变器模型预测共模电压抑制方法[J]．电工技术学报，2018，33(6)：1347-1355．

[9] 陈晓晓，程蓓，史丽萍．有源电力滤波器定频模型预测电流控制[J]．电力电子技术，2017，51(4)：57-60．

[10] 赵贺，李子矝，闫浩然，等．基于模型预测控制的微电网经济调度[J]．电网与清洁能源，2017，33(9)：119-123．

[11] 叶嘉俊，魏焕政，李牧星．交直流混合微电网中双向AC/DC变换器模型预测控制策略[J]．广东电力，2017，30(4)：125-130．

[12] 段洁，孙正龙，张秀琦．基于模型预测控制的互联电网阻尼控制[J]．广东电力，2016，29(6)：78-81，86．

[13] 冀红超，吴文昌，刘永春．电流频谱可控的单相并网逆变器模型预测控制方法[J]．分布式能源，2018，3(2)：47-52．

[14] Rameshkumar K，Sakthivel A，Vijayakumar P，et al．Performance analysis of model predictive control for voltage source inverter[J]．International Conference on Green Computing Communication and Electrical Engineering (ICGCCEE)，Coimbatore，2014：1-5．

[15] Mohamed I S，Zaid S A，Abu-Elyazeed M F，et al．Model predictive control：a simple and powerful method to control UPS inverter applications with output LC filter[J]．Saudi International Electronics，Communications and Photonics Conference，Fira，2013：1-6．

[16] 陈宁宁，宋子豪，汪泽州．模型预测控制在光伏并网逆变器中的应用[J]．电气技术，2017(4)：79-83．

[17] 张保程，徐艳平，周钦．基于广义双矢量的PMSM模型预测电流控制[J]．电气传动，2017，47(3)：17-20．

[18] 徐艳平，王极兵，王建渊．考虑预测误差的改进双矢量模型预测电流控制[J]．电气传动，2018，48(9)：62-66．

[19] 周迎春，胡志军，黄辉先．虚拟矢量模型预测控制抑制逆变器输出共模电压[J]．山东农业大学学报(自然科学版)，2018，49(5)：875-879．

Research on Semi-vector Predictive Control Strategy of Active Power Filter

GONG Jing, ZHANG Qiaojie

(School of Automation, Beijing Information Science & Technology University, Haidian District, Beijing 100192, China)

Aiming at the problems of limited selection range of voltage vector and low accuracy of current tracking in the classical model predictive current control algorithm, an improved model predictive voltage control algorithm was proposed. The better voltage vector was obtained by rolling optimization, and usings/2 for the better voltage vector ands/2 for zero vector to achieve the half amplitude vector. The optimal voltage vector was chosen according to the evaluation function of the two vectors. Adding only one voltage vector per period could effectively reduce the error between predicted voltage vector and actual voltage vector, realized the accurate tracking of harmonic current, and improved the compensation performance of active power filter. Simulation results showed the proposed improved model predictive voltage control algorithm is more accurate than the classical model predictive current control algorithm in tracking the reference current. After compensation, the harmonic content in the grid-connected current decreases from 4.86% to 3.32%, and the grid-connected unit power factor can be achieved under both steady-state and dynamic conditions.

model predictive control; active power filter; current harmonics; optimal voltage vector

10.12096/j.2096-4528.pgt.18258

2018-12-25。

龚静(1994)，女，硕士研究生，研究方向为电力电子变换电路及控制技术，1156294271@qq.com；

张巧杰(1978)，女，博士，副教授，主要从事电力电子与控制技术研究，qiaojiezhang@163.com。

龚静

(责任编辑 辛培裕)