密度线性方程式的理论误差探析

陈一军，成刚虎

(西安理工大学 印刷包装与数字媒体学院，陕西 西安 710048)

密度线性方程式[1-2]，包括蒙版方程和灰平衡方程，也被称为彩色复制方程[1-4]，是重要的色彩平衡分析模型和工具，在印刷工程领域得到了广泛的应用。前者作为电子分色、制版修色、以及专色油墨配置[5-8]的理论基础，支撑着密度体系下的印前工艺；后者作为印刷质量分析中不可或缺的工具[9-17]，在过程控制中发挥着独特作用。

但是，在科学实验与生产实践中，经常出现与密度线性方程不相符合的现象[1-2]。随着印刷质量需求的不断提升，密度线性平衡方程存在的问题逐渐凸显出来。

针对密度线性方程在应用中出现的问题，业界一直在不断寻求着产生误差的工程原因和改善途径[6,12]。1953年，美国学者Evans曾建议方程组中加入常数项进行修正。1962年另一位美国学者Pobboravsky提出了一组高阶非线性方程组，以求提高密度平衡分析求解精度[1-3]。直至近年来，国内外学者依然进行着探索分析[8,16-17]。这些研究有的针对配色精度问题进行了蒙版方程应用分析和模型改进[5-6,18-19]，有的针对灰平衡控制进行了密度线性方程的应用研究[9-12]、误差分析[13-16]和改良探索[16-17]。

不可否认的是：这些研究都一定程度上提高了密度线性方程特定条件下的应用精度[5-6,16-17]，但究其本质都是改良性的，受制于固有的认识局限，很少有人对其理论基础提出过质疑。因此，虽然某些场合应用误差得到控制，也注定是很有限的。

其实，密度的可加性与比例性失效问题，早已得到关注，并长期出现在教科书中[1-3]。但是，之所以会产生失效问题，究竟是因为实际印刷(包括实验)中印刷材料的不理想造成的？还是模型的科学性存在瑕疵引起的？这些问题一直悬而未决。遗憾的是，这些问题却并未引起业界足够的应有重视。鉴于此，在前期研究[20-22]的基础上，作者开展了本文的理论探索分析。

1 密度线性方程式的发展演变及其理论基础

密度是一个光学概念，被定义为透射(或反射)率的倒数的对数[1-3]，用以度量材料吸收光辐射的程度。

1.1 密度平衡方程式的发展演变

密度平衡方程式伴随着印刷技术的发展而产生，根据不同的应用场合而具有不同的形式，但是其本质都一样。照相蒙版方程的发展渐进过程就是密度平衡方程式的发展历程。

伴随早期的照相制版工艺理论，产生了第一代照相蒙版模型。

在这个模型中，纸张和油墨都是理想化的。即假定纸张不产生光吸收，而油墨具有理论上的选择性吸收特性。那么，原稿红、绿、蓝三色密度DR、DG、DB即为青、品、黄三色油墨主密度C、M、Y。

亦即：

(1)

显然，依据这样的关系进行分色制版会造成很大的误差，因为没有考虑油墨的不纯洁性。于是，考虑实际油墨的选择性吸收不足以及不应有吸收的情况，就需要寻求新的蒙版模型。

分析可知，因为采用实际油墨进行印刷，获得的印刷稿上，每种单色油墨除了不尽吸收其互补色光线之外，还有对应的不应有吸收。因此，蒙版分色时，原稿的分色密度(即蒙版密度)除了含有主密度外，还应该考虑两个副次密度的贡献。也就是说，在蒙版方程(1)中，需要计入另外两种油墨的副次密度的作用。那么，究竟应该如何考虑副次密度的影响呢？

因为密度被认为并且被证明是可加的，于是，“根据密度相加原理，三色油墨叠印的合成密度等于各单色密度之和”。与此同时，为简化计算，引入了密度的比例性设定，即假设密度具有比例性特征。于是就产生了蒙版方程[1—4]：

(2)

式中：cG、cB、mR、mB、yR、yG分别代表各色油墨副次密度与主密度的比例系数。

显然，式(2)是一个线性化密度平衡方程式，其一般通用式[1-4]为：

(3)

式中：ψY、ψM、ψC分别代表黄、品、青三原色油墨印刷匹配给定色密度时所需的各色油墨比例；DYB、DMB、DCB分别代表蓝滤色片下黄、品、青油墨印刷实地块的密度；DYG、DMG、DCG分别代表绿滤色片下黄、品、青油墨印刷实地块的密度；DYR、DMR、DCR分别代表红滤色片下黄、品、青油墨印刷实地块的密度；DR、DG、DB分别代表红、绿、蓝滤色片下待配色块的密度。

只要将式(3)的右边替换成不同等级的中性灰分色密度DZR、DZG、DZB，就变成了灰平衡方程[1-3]。

1.2 密度线性方程式的理论基础分析

有了密度线性平衡方程，进行色彩分析，就有了理论依据[1,4]。而且，线性化处理之后，可操作性更强，也方便了工程应用。因此，一定意义上讲，在印刷工程由模拟(照相制版和主观分析)阶段走向数字化分析处理进程中，也发挥了积极作用。

但是，在密度线性方程式(3)中，密度的可加性与比例性是其核心技术支撑[1-4]。如果没有可加性支持，线性化平衡方程根本建立不起来。缺乏了比例性限定，虽然是线性方程，就会增加方程的求解复杂性，从而失去工程应用价值。

2 密度线性方程式的理论局限性分析

密度线性方程式之所以存在理论局限性，一方面是因为在其建立过程中凭借的密度可加性存在瑕疵，另一方面是因为为便于工程应用而强加的密度比例性设定存在原始误差。尽管目前国内所有的色彩学教科书都引用了可加性的证明过程[1-3]，表面看来似乎没有问题。但是，仔细研究可知，其理论依据还是存在问题的。

2.1 密度可加性及其理论依据

见图1，光通量为φ的光线通过两层物质后的合成透射率τ和合成密度值Dτ为：

(4)

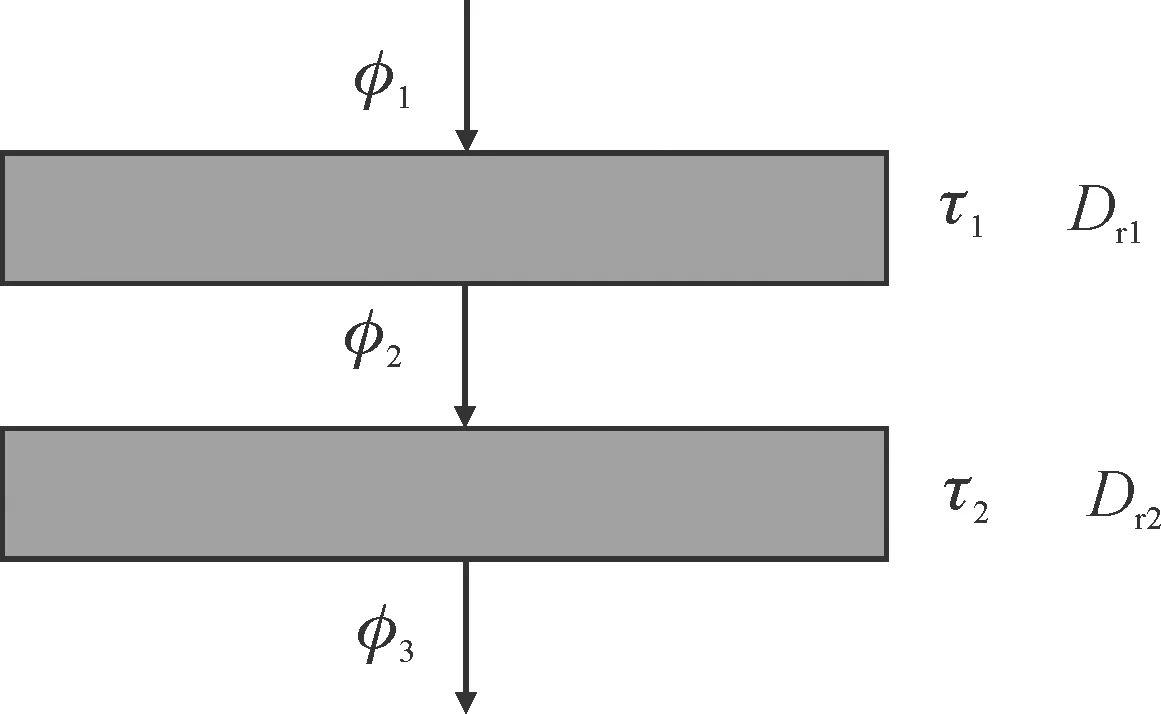
图1 多层叠合密度示意图[1]

以此类推，三色印刷时，有：

(5)

此乃密度的可加性及其理论依据。

据此，印刷行业就认为：“三色油墨叠印的合成密度等于各单色密度之和”[1-2]。

2.2 密度可加性的分析研判

尽管上述理论推导过程无可厚非，但是，一旦与其工程背景相结合，就会发现，密度可加性不具有一般意义，一旦被泛化，必然会因为条件不对称而引发数学逻辑问题和物理支持问题。

同样，密度的比例性设定也不合理，隐含了明显的逻辑错误，违背了光的可加性原理。

2.2.1密度可加性不符合数理逻辑

我们知道，半调印刷时，网点关系结构微观上有两种状态，即“网点并列”与“网点重叠”[2-3]。尽管对于各层油墨完全叠合时，方程(4)和(5)似乎成立，但是，仅仅依靠网点重叠(实地状态)时的可加性，并不能证明一般状态下的可加性。

在既有“网点并列”也有“网点重叠”的一般情况下，区域密度是两种情况的合成，而区域密度的形成机理较单一状态的合成要复杂一些[21-22]。

这里以双色叠印为例进行简化分析。面积率分别为a和b的两色版叠印，网点重叠面积率为c，那么空白区域面积率即为1-a-b+c，其网目调微观结构模型见图2。

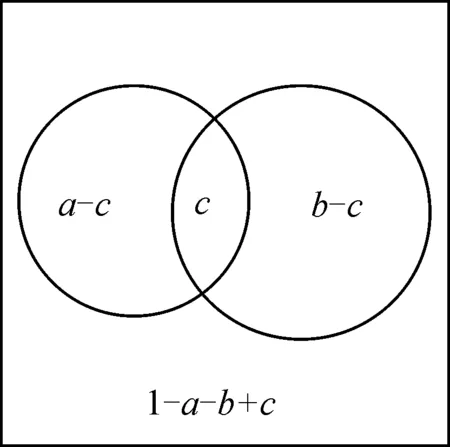
图2 双色叠印的微观结构模型(不同区域面积率关系)

如果认为纸张是理想化的，不吸收光线，即没有密度，那么，网点密度与实地密度的关系可以根据Murray-Davis公式[1-3,20]取得。

第一色单独印刷时，有：

(1-a)+a10-Ds1=10-Dτ1

(6)

第二色单色印刷时，有：

(1-b)+b10-Ds2=10-Dτ2

(7)

两色叠印后，依据色光加色法，可以推知：

(1-a-b+c)+(a-c)10-Ds1+(b-c)10-Ds2+c10-Ds12=10-Dτ

(8)

如果计入纸张影响，即为：

(1-a-b+c)10-D0+(a-c)10-Ds1+(b-c)10-Ds2+c10-Ds1=10-Dτ

(9)

式中：D0、Ds1、Ds2和Ds12分别表示纸白、第一色、第二色以及叠印色的实地密度；而Dτ即为两色叠印色网点密度。

从式(8)～(9)可以看出: 无论是完全网点重叠(即a=b=c)，或是两色网点完全并列(c=0)，还是既有网点重叠又有网点并列的一般情况，只要不是两色都是实地，那么，即使Ds1+Ds2=Ds12，一般情况下也不存在Dτ1+Dτ2=Dτ。

也就是说，线性可加性不具有一般性。即使实地条件下满足密度可加性，网点密度也不会服从可加性。

另外，从式(9)可以看出，可加性设定引起的计算误差，不但与纸张特性有关，也与网点大小有关，还与决定叠印网点相对关系的加网参数有关。

2.2.2密度可加性偏离了共同的物理基础

密度是光学概念[1-2]，应用于具体的工程实际时，为了使测量结果具有一致性和可比性，总是要设定相应的物理条件。在印刷行业，实用中，一般是以标准光源及其标准照射条件、测量环境为限定条件的[1-2,18,22]。

为什么被严格证明了的式(4)，与印刷实际不相符合呢？

其根本原因在于，油墨具有选择性吸收特性，油墨反射密度既具有光谱依赖性，也具有光强依赖性，随光谱成分的改变而改变，也随光源照射强度的改变而改变。

在多层油墨叠合[1,3-4]呈色机制中，各层油墨吸收光线的光谱范围和光强是依次递减的。当光线照射在墨层上时，首层油墨最先进行选择性吸收，接着才能依次透射给下面各层油墨。但是，光线经首层墨层吸收后，其光谱成分与光强都减小了。也就是说，第二层油墨的入射条件已经变化了。同样，第三层墨层的光照频谱范围更小了，光照强度更弱了。因此。除首层油墨外，其余各层油墨的实际入射条件都与首层大不相同了，其实际阻光系数、或者透光系数减小了，已经与首层油墨没有可比性，因此其有效密度并没有单独测量时那么大。因此，才会出现“实际印刷中，几种油墨叠印时，用同一滤色片测得的叠印色块的密度值往往明显比各单色油墨密度值之和要小”[1]的情况。

在式(4)的证明中，Dτ1与Dτ2根本不具有物理意义上的可比性。因为两者的照射条件发生了变化[19]。严格意义上讲，此时的Dτ2已不再是标准条件下的密度了，而是另一种照射条件下的“密度”值。这种情况下，如果要利用这种所谓的可加性，就必须附以不同照射条件下的“密度”值。这显然是不现实的。一是我们根本就不可能精确模拟出变化万千的照射条件；二是即使可做到精确模拟测量，那么需要积累的不同条件下的“密度”值数量庞大，可操作性极其有限。

综上分析，在进行可加性证明的逻辑分析中，忽视了其物理基础的不一致性。如果承认这种所谓的可加性，必然会造成理论误差。

2.2.3密度可加性固有理论问题的旁论佐证

其实，在印刷领域，几个常识性现象和相关结论也佐证了可加性存在理论问题。

1)印刷色序的不同，呈色效果会产生较大差异[2]。除了首层反射影响外，可加性失效也是其中重要因素。因此，人们不得不通过认真分析进行色序设计。

2)网点并列与网点重叠不具有同样的呈色效果[1-2,21-22]，因此，才出现了复杂的印刷呈色模型——Neugebauer方程，同时，人们才不得不重视加网对印刷呈色的影响[7]。

3)即使是理想的条件，密度也不服从可加性。比如，理想的青墨和品墨实地叠印得到理想的蓝色实地块。但是，显然其密度并不符合可加性，即lg1.5+ lg1.5并不等于lg3；可见，那种认为理想条件下可加性无可厚非[2]的认识是存在错觉的。

4)线性化的Lambert-Beer方程在印刷领域是不成立的。之所以如此，其实正是因为密度不具有线性可加性所致。因为，如果用单色印版(采用相同油墨)在纸张上印两次，就得到了厚度加倍的印刷样张。假定纸张是理想的，那么，按照可加性，样张上色块的密度就应该翻倍。可是，这样的结论显然是荒谬的[1]。这也从侧面告诉我们，密度并不服从可加性。

2.3 密度比例性的逻辑考察

密度比例性的理论误差主要来源于网点密度与实地密度之间复杂的非线性关系[20]。

2.3.1密度的比例性概念及其内涵

所谓的密度的比例性，就是“各单色油墨在印刷网点面积率不同时，用红、绿、蓝滤色片测得的密度值，相互间保持比例(线性)关系。或者说，各色油墨副次密度与主密度之比为常数”[1-2]。

显然，密度的比例性就是对油墨不纯洁现实性的接受和设定。对于理想的油墨，其主密度为无穷大，副次密度为0，无比例性可言。

2.3.2密度比例性的理论误差研究

根据[5]的研究可知，单一油墨印刷网点面积率为a的色块，油墨实地密度为Ds(与之对应的反射率为ρs)，空白区域的面积为1-a，纸张密度D0(对应反射率ρ0)，那么，根据光通量的可加性，网目调总反射率和主密度[1-2,20]为：

ρ=(1-a)×ρ0+(a×ρs)

(10)

即：

(1-a)10-D0+a10-Ds=10-Dτ

(11)

显然，这一关系对于油墨的主、次密度都是成立的。即：

(1-a)10-D01+a10-Ds1=10-Dτ1

(12)

式中：D01、Ds1分别为对应的纸张副次密度和油墨实地块副次密度。

所谓密度的比例性，在这里就意味着Dτ1与Dτ之比应该等于Ds1与Ds之比[1]。但是，根据式(11)～(12)，不难推出：

(13)

式(13)表明，无论D0是否为0(即无论是否考虑纸张的不纯洁性)，理论上讲，密度的比例性都是不存在的；而且，网目调区域内，任一油墨副次密度与主密度之比都是关于纸张密度的函数，而且随面积率a的变化而非线性变化。可见，密度不具有定常比例性。

3 可加性与比例性设定的误差分析

密度线性方程式依靠密度可加性而建立，凭借比例性设定而简化。上述理论剖析表明，这种密度的线性化处理必然地引入了系统误差。但是，理论上存在的瑕疵究竟会产生多大的实际影响呢？这里借助仿真分析方法，仅仅对可加性与比例性设定所引起的系统误差及其影响因素进行分析考查(其实验辨析可参看文献[1])。

3.1 实验及其实验数据获取

对印刷色空间进行12级分割，设计了四色印刷测试版，在方正印捷C1060彩色数码印刷机上进行了印刷实验，在实验室测取了相关数据。其中，相关色样的印刷实测平均数据见表1。

表1 仿真分析用标准实地块的印刷实测密度

3.2 比例性理论误差的仿真分析

基于表1标准实地色块实测分光密度数据，借助于式(11)～(12)，取得青品黄三色色块各灰度级的主次密度仿真计算值见表2。

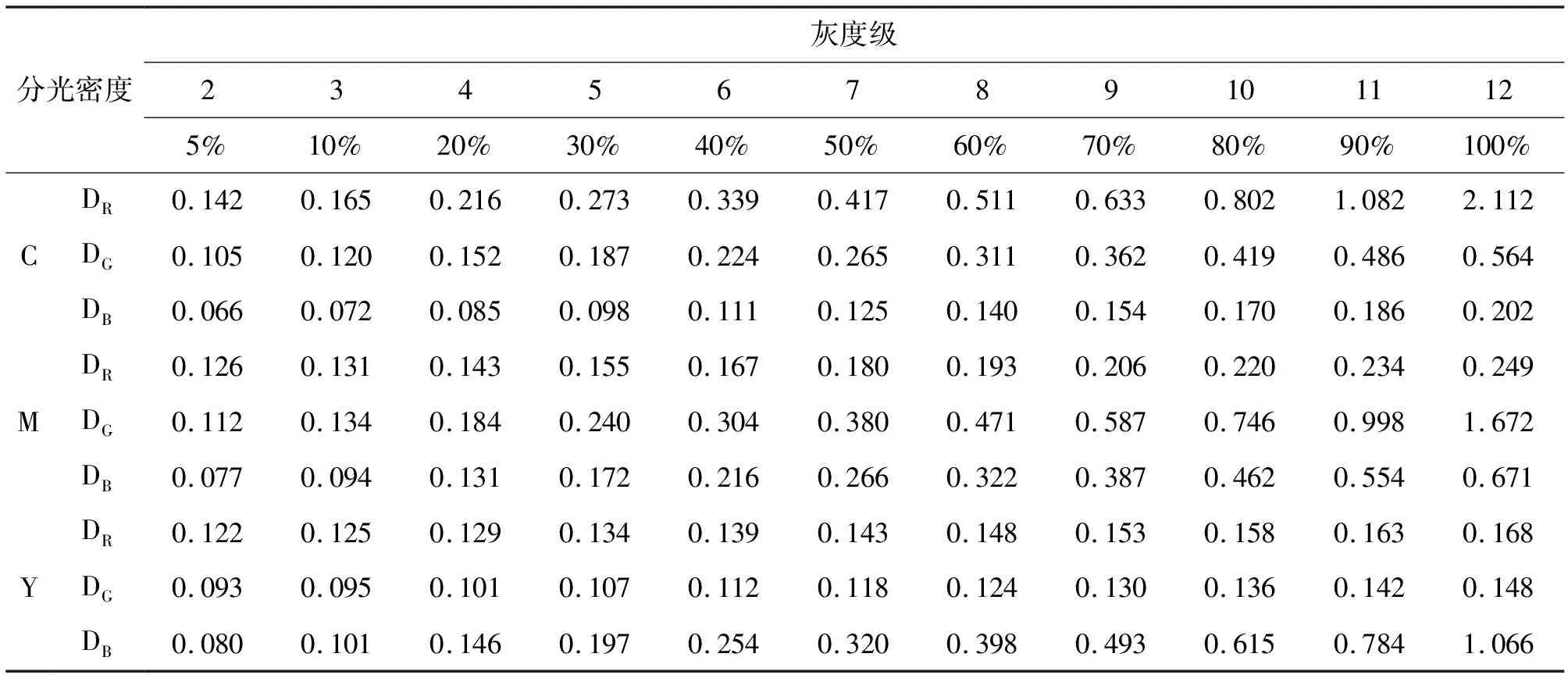
表2 青品黄三色各灰度级的主次密度仿真计算值

基于表2数据，依据式(13)，青品黄三色各灰度级的主次密度之比见图3。显然，青品黄三色主次密度都不服从比例性假定。

图3 青品黄三色主次密度之比变化曲线

3.3 可加性理论误差的仿真分析

限于篇幅，并为方便计算，这里以线型网[4,22]为例，仅以双色叠印密度进行仿真分析。

依据表1数据，依靠式(9)，取得红绿蓝三复色各灰度级主次密度，结果见表3。其变化规律见图9，并将其与各单色相加而得的合成密度进行比较。

无论是青品叠印的蓝色、品黄叠印的红色、还是青黄叠印的绿色，其合成密度都与仿真计算密度存在一定差异。而且差异大小在不同灰度级上表现出不同的量级。

采用不同的油墨、纸张、以及加网参数，都会取得类似的分析结果。尽管结果会有所差异，但是，都能取得相同的结论。这就是：密度比例性与可加性总是存在着误差。其差异性体现了理论误差的可变性与依赖性。

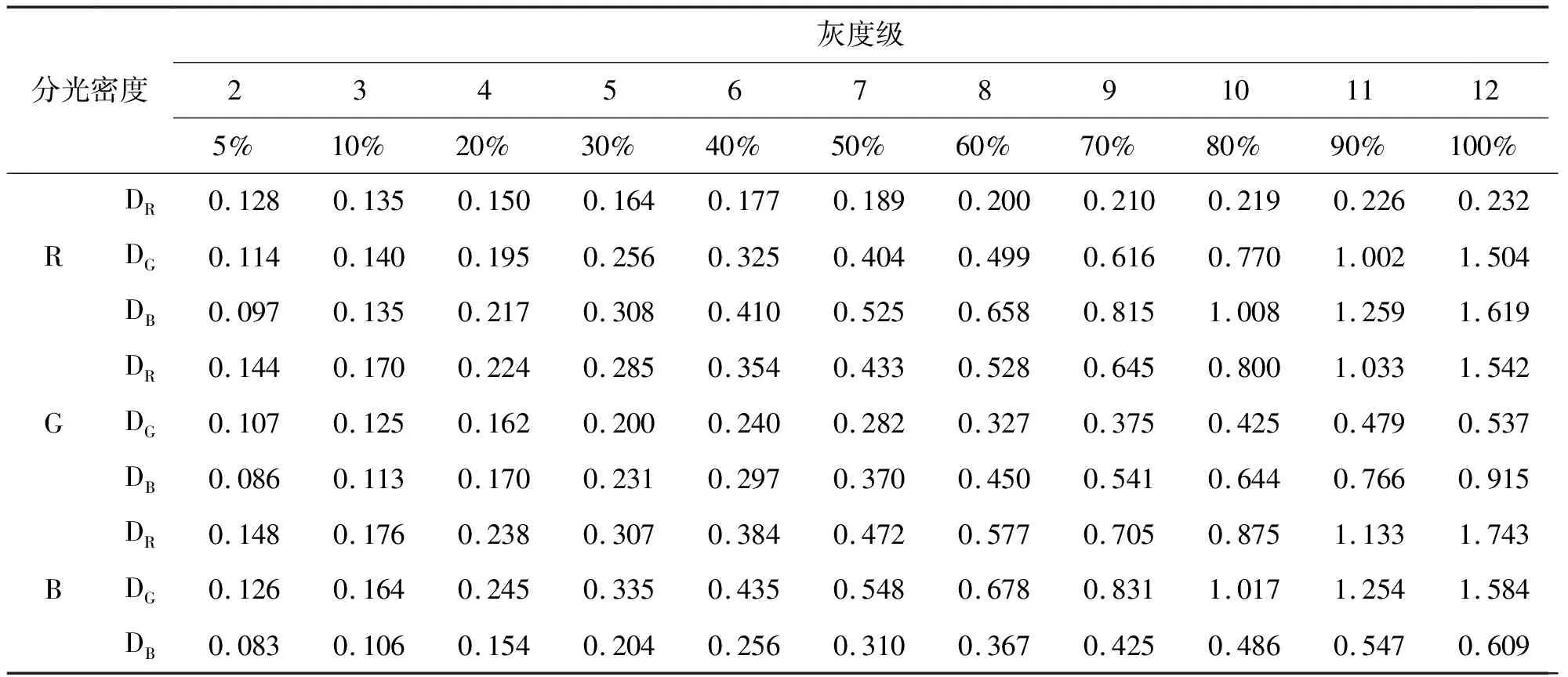
表3 红绿蓝三色各级密度计算值

图4 红绿蓝三色合成主密度与仿真计算密度之比较曲线

4 研究结论

立足业界广泛接受的色光加色法[1-4,20]，本文在不计工艺误差(工艺过程误差、测量误差等)基础上，仅仅从理论角度考察了密度线性方程式赖以生存的物理基础，对其应用误差进行了理论探究、仿真分析，取得了如下研究结论。

1)密度虽然具有随墨层增加同向变化的特性，但是密度可加性在理论上是不存在的。不但缺乏共同的物理基础支持，而且也不符合数理逻辑。可加性设定产生的理论误差受阶调浓淡层次以及加网参数的影响。

2)密度的比例性在理论上也是不存在的。受制于纸张的吸收特性、网点面积率的影响，比例性设定具有变值系统误差特征。

3)密度线性方程式存在理论误差，密度不存在线性关系，其误差影响无法消除。进入色度评价时代，建议停止使用密度线性方程式。