板中Lamb波激励响应计算方法*

许西宁， 余祖俊,2， 邢 博， 朱力强,2

(1.北京交通大学机械与电子控制工程学院 北京，100044) (2.北京交通大学载运工具先进制造与测控技术教育部重点实验室 北京，100044)

引 言

传播超声导波[1-3]的波导介质一般具有以下特点，纵向长度很长、横截面形状一致，如薄板、杆、管道和钢轨等[4-6]。超声导波在波导介质中传播时可以覆盖整个介质的横截面，且传播距离远，因此超声导波是一种非常有前景的监测手段。基于超声导波，可以有效定位结构损伤的位置、程度[7-8]和类型。

在平板中传播的Lamb波[9-11]是导波的一种，近年来被广泛应用于复合材料结构[12-13]的无损检测[14-17]中。频散、多模态是导波的基本特性，在同一频率下有多个可传播的导波模态，在采用Lamb波检测薄板材料内部缺陷时，需要研究各个模态的激励方法及传播规律。采用计算机仿真研究方法可以节省大量的时间和资源，三维有限元仿真是最常用的方法，且有比较成熟的商业软件，如ANSYS等。激励响应计算方法是研究Lamb波传播特性的另一途径，基于半解析有限元方法[18-19]，对于薄板介质，在横截面作一维有限元离散，当仿真较远距离、三维离散单元非常密集时，采用激励响应计算方法可以节省大量的计算量、时间和内存。

在激励响应计算时，首先基于半解析有限元方法建立薄板中Lamb波的一般均质波动方程，通过求解标准特征值问题提取薄板中导波的模态数据，建立系统函数模型。通过傅里叶变换得到施加激励信号的频域值，将频域值代入系统函数模型，进行加权求和，计算得到频率-波数域中的激励响应。应用傅里叶逆变换，将系统频率响应从频域转换成时域，得到远离波源位置处的瞬态响应结果。激励响应计算方法可以求解任意横截面波导介质的时间瞬态响应，该方法可推广用于计算导波在钢轨或管道中的传播过程，具有较好的通用性。

1 模型定义

在计算薄板中Lamb波的激励响应时，首先要建立薄板的系统函数模型，这里定义薄板的横截面为y-z坐标平面，Lamb波传播方向为x方向，如图1所示。

图1 薄板中Lamb波传播的半解析有限元模型Fig.1 Semi-analytical finite element model of Lamb wave propagation in a plate

用式(1)来表示薄板的系统函数模型[4]

(1)

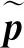
(2)

(3)

其中：K1,K3,M为Lamb波一般均质波动方程中的刚度矩阵。

对激励信号F(t)作傅里叶变换

(4)

经卷积计算，可以得到V(y,z,f)为

(5)

对V(y,z,f)作傅里叶反变换，可以得到激励信号的响应结果。

2 建立系统函数模型

薄板中Lamb波激励响应的时域波形是通过频域计算结果的反傅里叶变换获得的，在计算频域的激励响应结果时，首先要建立薄板的系统函数模型。该模型是由所有在薄板中可传播的Lamb模态组合构建的，如式(1)所示，其中主要用到了波动方程的刚度矩阵和各模态的振型数据。通过半解析有限元方法可以建立薄板中Lamb波的一般均质波动方程，获得刚度矩阵，求解波动方程可以进一步得到Lamb波各传播模态的振型数据，由刚度矩阵和振型数据可以建立薄板的系统函数模型。

半解析有限元方法可用于建立任意横截面波导介质中导波的传播模型，对于薄板结构而言，只需在横截面作一维有限元离散，沿Lamb波传播方向质点的位移则用简谐波指数方程的形式表示，通过标准的数学运算，可以获得板中Lamb波的一般均质方程。

图1为无限宽自由薄板的模型，导波沿x方向传播，每个质点的位移用u表示，应力和应变分别用σ，ε表示。

(6)

应变与位移的关系可用式(7)表示为

(7)

其中

薄板中坐标为(x,y,z)的任意质点，其随时间变化的位移值，可以用简谐波时空域的函数表示[6]为

(8)

其中：eiξx为空间域的值；ξ为波数；eiωt为时间域的值；ω为频率。

在有限元离散时，将薄板的横截面等效为无限宽，仅在z方向作一维有限元离散，如图2所示。3个节点组成一个单元，每个节点包含x,y,z三个自由度。

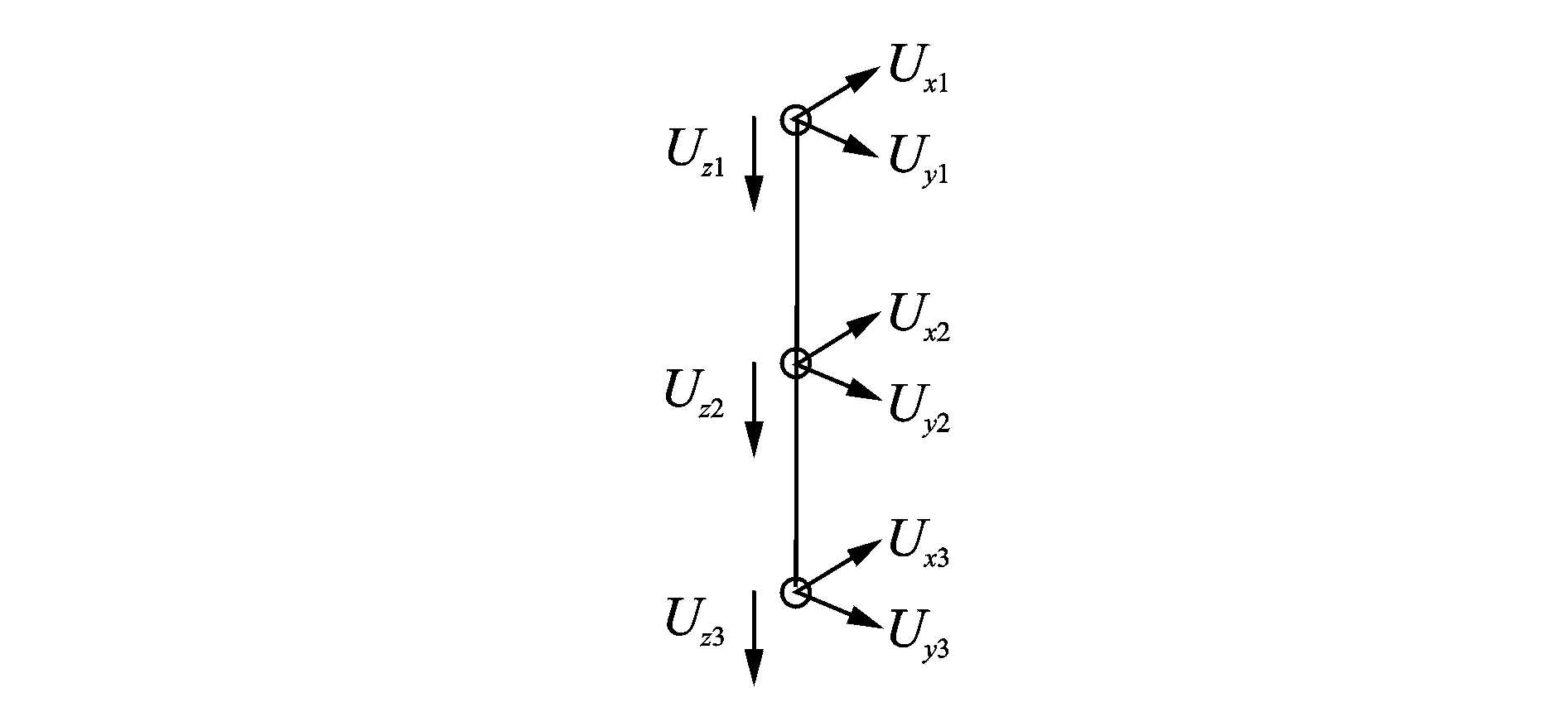
图2 节点单元Fig.2 Node element

对于离散后的单元，其内部任意一点的位移可以表示[6]为

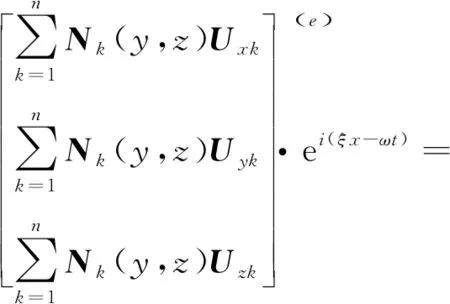
N(y,z)q(e)ei(ξx-ωt)

(9)

其中：N(y,z)为形函数矩阵；q(e)为节点位移矢量。

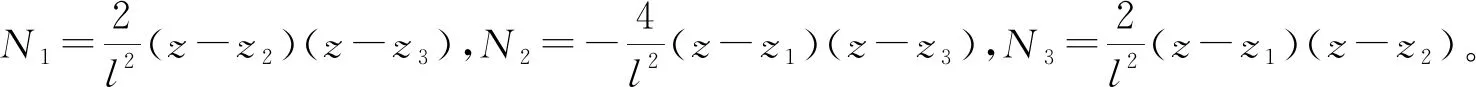
经数学运算和推导，最终可得到以下一般均质波动方程[20]为

[K1+iξK2+ξ2K3-ω2M]MU=0

(10)

其中：下标M代表系统的自由度数；U为振型矢量；K1,K3,M为刚度矩阵。

求解式(10)可以得到波数ξ、频率ω的值，从而绘制Lamb波相速度频散曲线，如图3所示。横轴为频厚积，纵轴为相速度。频厚积即频率与平板厚度的乘积，Lamb波在不同频厚积平板中的传播特性是不同的。

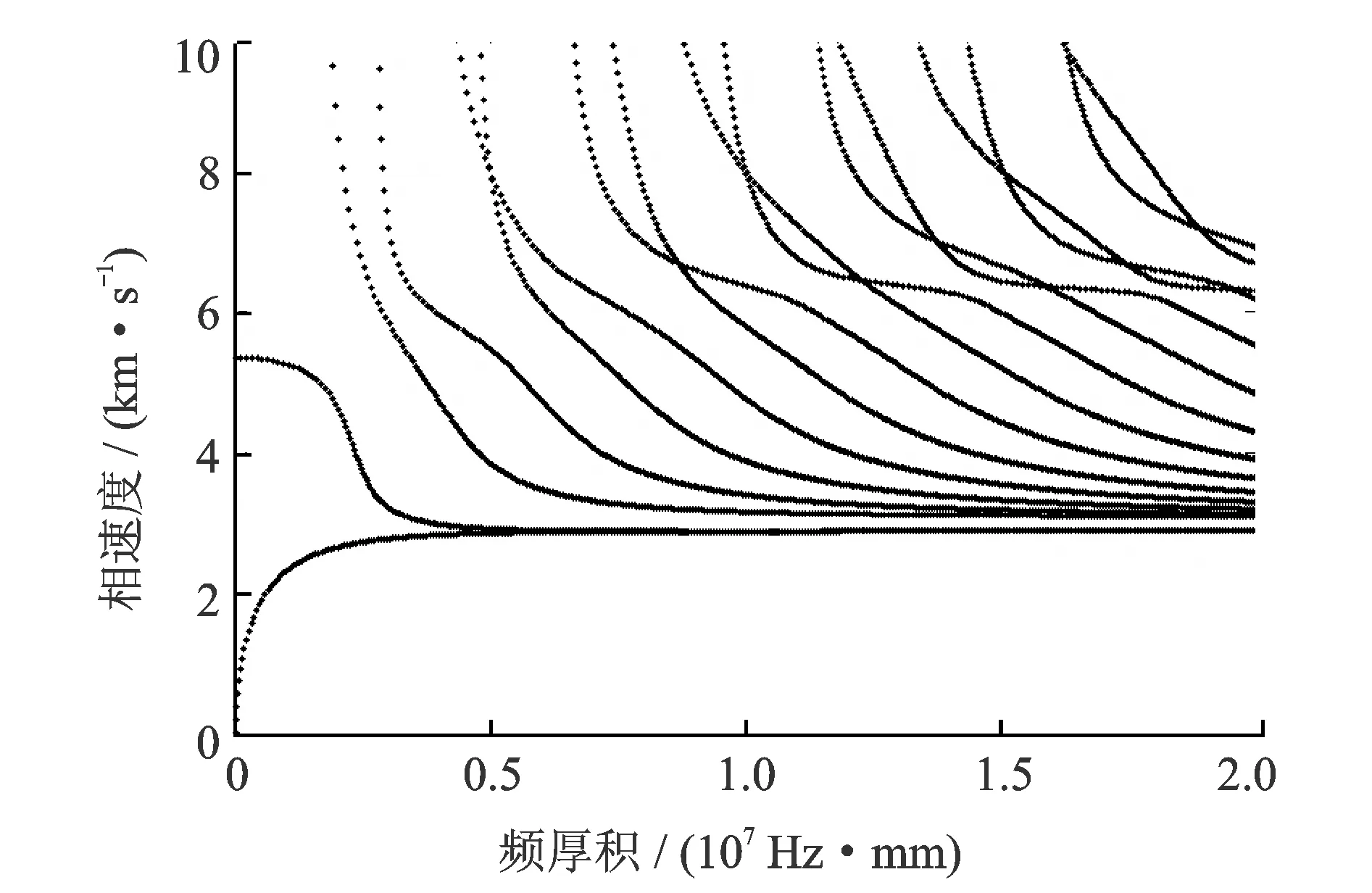
图3 相速度频散曲线Fig.3 Phase velocity dispersion curves

由式(11) 可求出Lamb波群速度值，并绘制频散曲线，如图4所示。

(11)

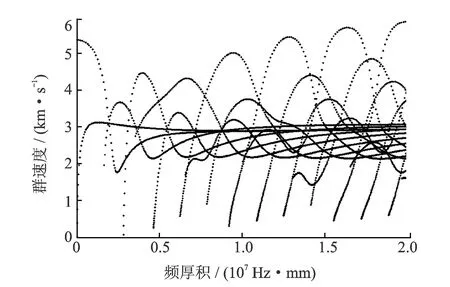
图4 群速度频散曲线Fig.4 Group velocity dispersion curves

求解式(10)，可得到振型矢量U，以及刚度矩阵K1,K3,M，代入式(3)中，可得到B矩阵，将U,B代入式(1)中，可得到系统函数模型H。

3 激励响应求解

以2.5 mm厚铝板为例，求解激励响应结果。在铝板左侧中心点沿x方向施加激励信号，分别计算距离施加点100和200 mm位置的响应信号，如图5所示。

图5 激励响应计算布置图Fig.5 Layout of excitation response calculation

激励源为三角波信号，如图6所示。三角波信号频谱较宽，通过分析响应信号可以得到多个频率点的群速度，进而和群速度频散曲线进行比对验证。

图6 激励信号Fig.6 Exciting signal

首先对该激励信号进行傅里叶变换，得到三角波信号的频谱，如图7所示。

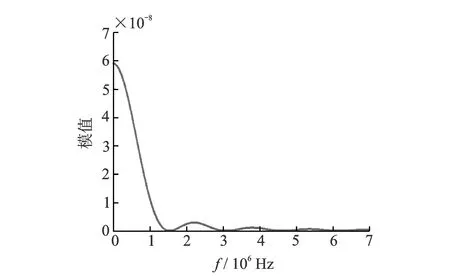
图7 三角波信号频谱Fig.7 Spectrum of triangular wave

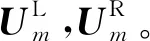
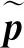
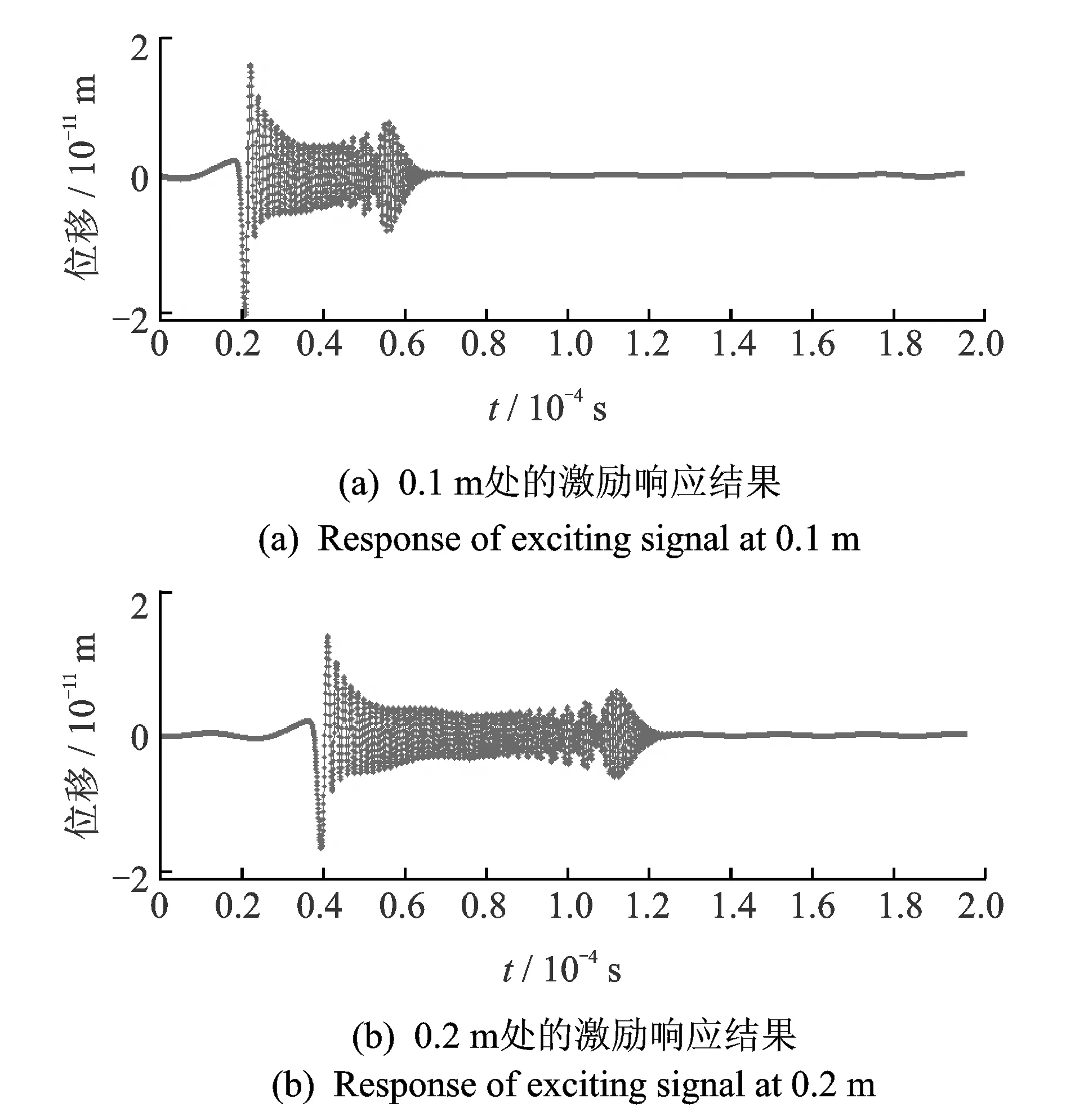
图8 激励信号响应计算结果Fig.8 Response of exciting signal

由图可见，Lamb波在传播过程中波包变宽，出现了频散现象。以上求解采用半解析有限元方法，共耗时约175 s。采用有限元分析软件同样可以进行激励响应分析，如用ANSYS软件，针对300 mm长，200 mm宽，厚度为2.5 mm的铝板，网格大小设为0.125 mm×0.125 mm×10 mm，求解过程需耗时28 h 17 min。由此可见，采用半解析有限元方法可以大大节约计算时间。

对图8中的激励响应结果进行小波分析，得到小波时频图，如图9所示。

图9 小波分析结果及峰值点Fig.9 Wavelet analysis results and peak points

图9(a)，(b)分别是0.1，0.2 m处激励响应信号的小波分析结果，在图中用星号标注了不同频率的峰值点，根据图9(a)，(b)中峰值点的时刻，可以计算出不同频率下的Lamb波群速度值，计算结果如表1所示。

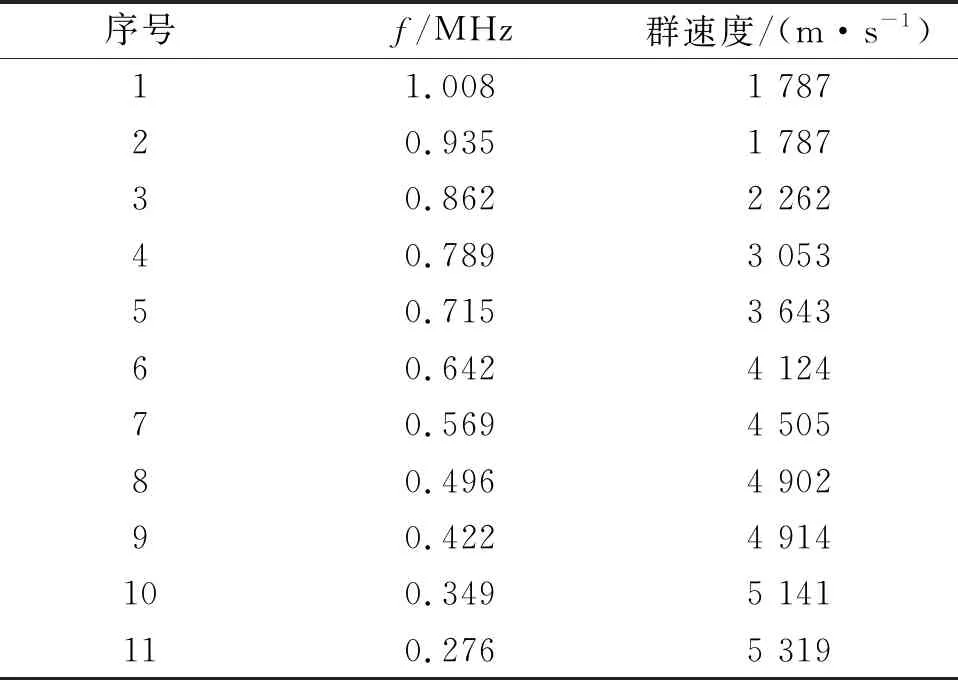
表1 不同频率下的群速度值

激励响应计算共求解得到11个群速度值，在Lamb波群速度频散曲线上叠加绘制了这11个群速度值，在图10中用圆圈绘出。从图中可以看出，11个群速度值均在S0模态的群速度频散曲线附近，在2.5 mm厚铝板中心施加三角波激励信号，可以激励出对称模态的Lamb波。

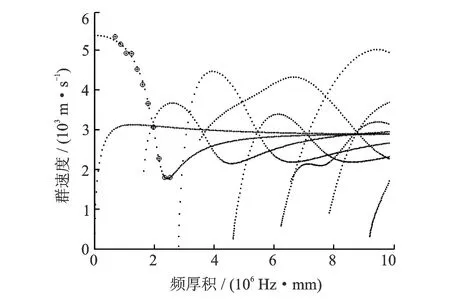
图10 激励响应计算得到的群速度值Fig.10 Group velocities calculated by excitation response

4 实验分析

下面将通过实验进一步验证激励响应计算结果。实验时选用2.5 mm厚的1060工业纯铝板，铝含量为99.6%，采用汕头超声公司的1 MHz超声波斜探头作为Lamb波的发射、接收探头，探头入射角为45°，型号为1P13*13 K1。探头采用耦合剂粘在铝板上，探头布置如图11所示。

图11 实验布置图Fig.11 Experimental layout

在发射探头T1施加高压脉冲信号，激励Lamb波在铝板中传播，接收探头R1,R2采集的波形如图12所示。上图为距离T1发射探头40 mm位置处，探头R1接收到的波形，下图为探头R2接收的波形图，R2距离T1发射探头80 mm。

图12 接收信号波形Fig.12 Receive signal waveform

对接收信号做小波变化，可以得到R1，R2探头接收信号的时频图，其信号峰值的时刻分别为17.64，40.04 μs，接收探头间距40 mm，群速度值为1 785.7 m/s。

下面进行激励响应计算分析，在铝板表面，平行铝板方向施加激励信号，铝板厚度为2.5 mm，激励信号中心频率为1 MHz，如图13所示。

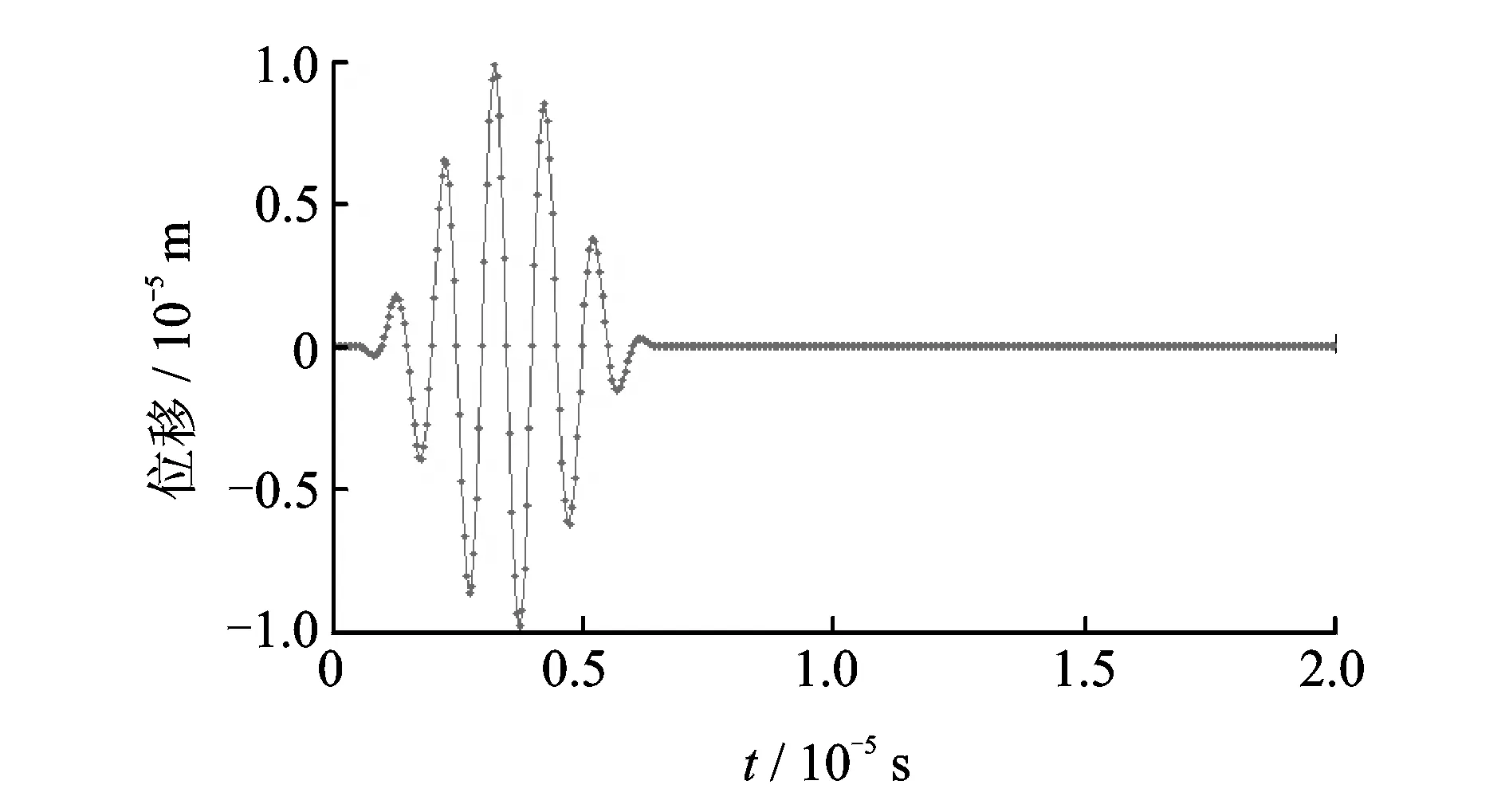
图13 激励信号Fig.13 Exciting signal

激励响应结果的计算点分别距离激励点位置80，120 mm，如图14所示。

图14 激励响应计算布置图Fig.14 Layout of excitation response calculation

激励信号频谱如图15所示。

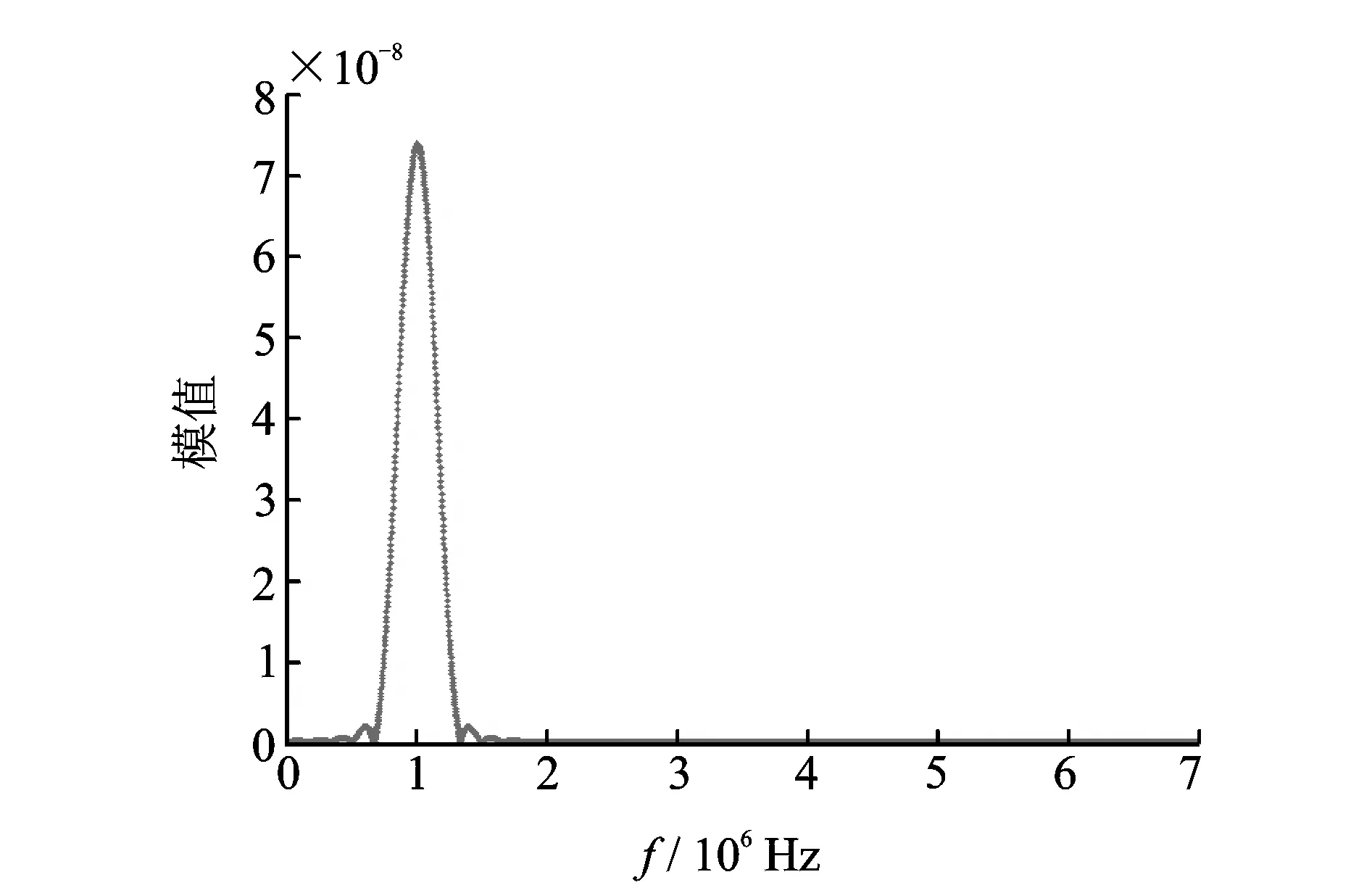
图15 激励信号频谱Fig.15 Spectrum of exciting signal

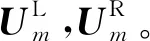
图16 激励信号响应计算结果Fig.16 Response of excitation signal

将图16中激励响应计算获取的波形，进行小波分析，结果如图17所示，图17(a)，(b)分别为图16(a)，(b)信号的小波分析结果。

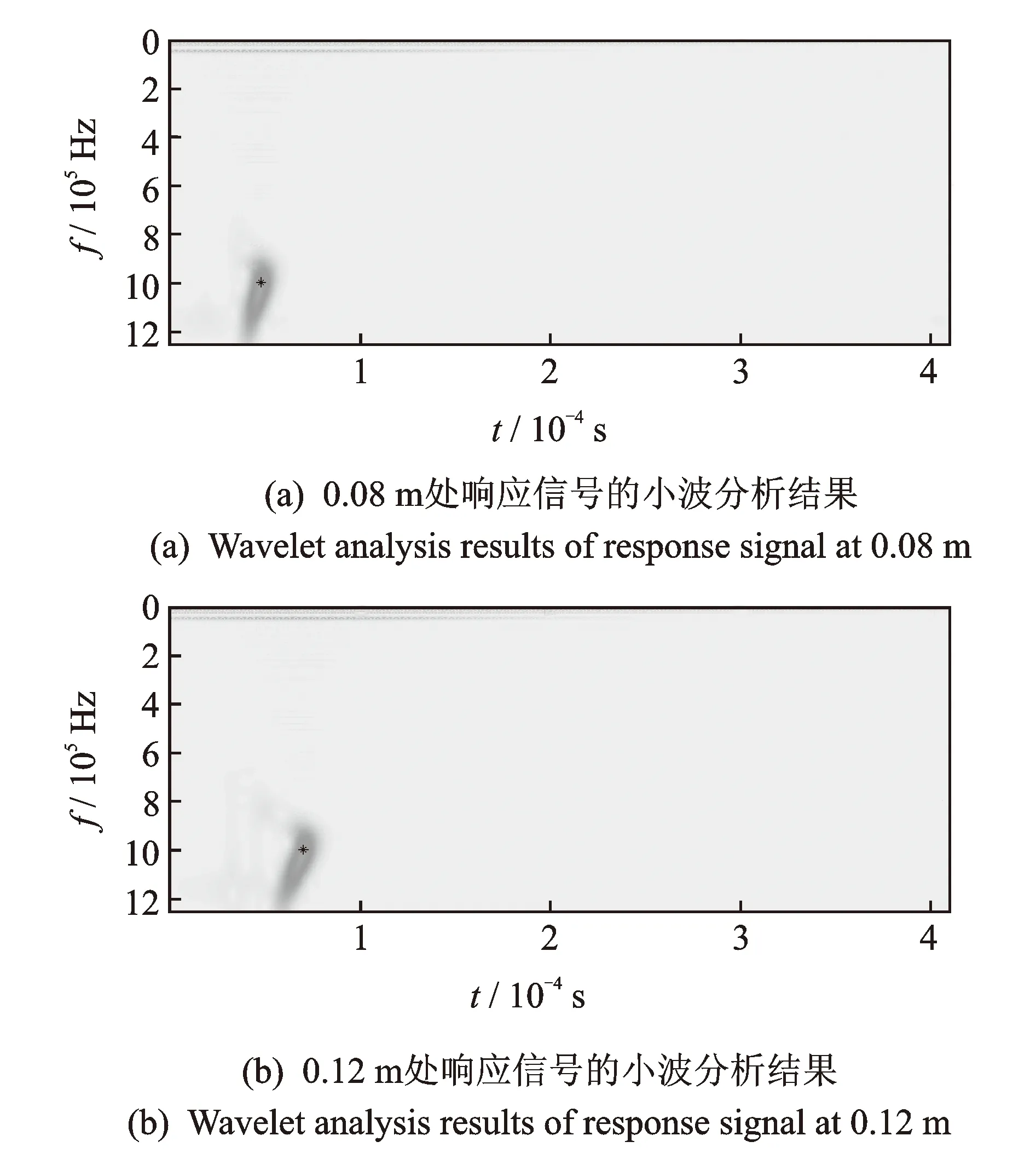
图17 小波分析结果Fig.17 Wavelet analysis results

由图17所示，距离激励位置0.08，0.12 mm处的响应波形的峰值点时间分别为47.85，70.1 μs，信号采样点间距0.04 m，时间差22.25 μs，可求得群速度为1 797 m/s。将此群速度值和群速度频散曲线对比，如图18所示。在图中频厚积为2.5 MHz·mm位置查找群速度频散曲线，与响应结果最相近的群速度值为1 776 m/s，为对称模态的Lamb波。

图18 激励响应计算得到的群速度值Fig.18 Group velocities calculated by excitation response

实验测量群速度值为1 785.7 m/s，激励响应计算群速度为1 797 m/s。实验和激励响应计算结果一致性较好，采用1 MHz斜探头，在2.5 mm厚的铝板上可以激励出S0对称模态的Lamb波信号。

5 结束语

通过半解析有限元方法求解薄板中Lamb波的一般均质方程，进而建立求解激励响应的系统函数模型，基于频谱叠加原理，可以计算薄板中Lamb波激励响应结果。经实验验证，激励响应计算与实验结果有很好的一致性，两种方法获取的数据，模态分析结论一致。激励响应计算方法是仿真分析波导介质中导波传播规律的一种数值计算方法，可以取代反复的实验环节，节省硬件成本，提高效率。该方法还可以仿真计算任意截面波导介质中导波的传播过程，具有较好的通用性。