基于超声波流量计的非理想流动粘黏性流体流量测量研究
檀盼龙,李益敏,韩思奇,邵 欣
(天津中德应用技术大学智能制造学院,天津 300350)
0 引言
超声波流量计具有精度高、无压降、重复性好以及可实现双向测量等特点,已经逐步取代传统机械流量计和其他类型流量计,在炼油企业及化工厂的原油运输中得到了广泛的应用[1]。时差法多声道超声波流量计利用超声波在测量介质中的顺流和逆流传播时间差计算出流体在声道所处平面的平均流速,再通过横截面积分方法计算获得流体的流量信息,算法简单,实用性强,在超声波流量计中的应用最为广泛[2]。
从1932年超声波流量计诞生至今,来自不同领域的研究者不断尝试通过各种技术手段提高超声波流量计的计量精度,如提高换能器的性能、优化放大器和滤波器电路设计、改进信号处理方式等[3]。对于多声道超声波流量计,声路的布置和积分系数的选取直接关系到流量计的测量精度。在过去的二十多年中,研究人员通过应用数学分析确定声道最优安装位置,同时通过人工神经网络、支持向量机以及Levenberg-Marquardt方法对各声道的积分系数进行优化求解,取得了良好的实验效果[4]。
但大多积分算法都是以理想流体为前提条件下设计的,没有考虑流体的黏性对于测量结果的影响,计算得到的声道位置以及权重系数是固定值,适用于流型对称分布的情况;但是由于不同生产地油品物性是不同的,而且在实际运输中管道结构、测量位置的变化都可能造成管道内流体出现非对称分布,此时采用传统积分方法进行计算容易造成较高误差[5-6]。
本文针对不同黏度的原油在实际运输中流量难以准确测量的问题,提出了一种基于带遗忘因子的最小二乘法的权重系数优化方法,并利用FLUENT进行仿真分析和实验测试。
1 超声波流量计的积分原理
1.1 时差法测量原理
时差法超声波流量计利用流体的流动对超声波在管道中传播时间的影响,计算流体的流速和流量。超声波在管道中的传播时间与流体的流动速度有关,在同等条件下,当超声波在流体顺流方向传播时的传播时间会减小,反之,则超声波在流体逆流方向传播时的传播时间会增大[7]。时差法超声波流量计利用超声波的顺逆流的传播时间差,实现对流体流动速度和流量的测量。时差法超声波流量计的测量原理如图1所示。
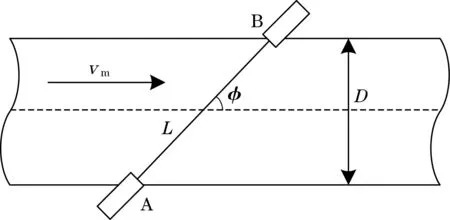
图1 时差法超声波流量计原理图
图1中,流体从左至右流动,其中vm为流体的流速,A和B为收发一体的超声波换能器,L为超声波换能器A、B之间的距离,φ为超声波探头之间连线与管道中线的夹角,D为管道的内径。
超声波在管道中的顺流和逆流传播时间为[8]:
(1)
(2)
式中:tup为超声波顺流传播时间;tdown为超声波逆流传播时间;cf为超声波在流体中的传播速度;tp为电路延迟时间。
由式(1)和式(2)可以求得超声波顺流和逆流传播的时间差为
(3)
在一般工业应用中,超声波在流体中的传播速度与流体流动速度之间存在较大差距,故式(3)可以近似等效为
(4)
进而根据式(4)可以求得流体流速:
(5)
1.2 声道超声波流量计积分原理
式(5)中所测得的流速是流体在超声波传播声道位置的平均流速,对于无黏性的理想流体,管道横截面的流体流速是一致、平均的,而在非理想状态下,流体存在黏性,管道内壁也有不同程度的粗糙度,造成了流体在管道中流动的非均匀性,处于湍流或紊流状态,因此管道横截面的不同位置的流速存在差异,只使用单声道方式进行流量测量将带来较大误差,提高测量精度的方式之一是采用多声道形式[9]。
多声道超声波流量计在工作过程中需要测量每个声道平均流速vmi(i=1,2,…,N,N为声道数),得到每个声道上的平均流速之后,通过与声道布局相对应的权重系数方案进行加权计算,得出流体的测量流量。
根据高斯数值积分原理,总存在积分位置x1,x2,…,xN和权重系数w1,w2,…,wN,使式(6)成立[10-12]。
(6)
所以在如图2所示的半径为R的圆形管道流量积分中,存在流速检测位置z1,z2,…,zN和权重系数w1,w2,…,wN,使得:
(7)
F(z)=l(z)v(z)
(8)
式中v(z)为z处的流体速度。
(9)
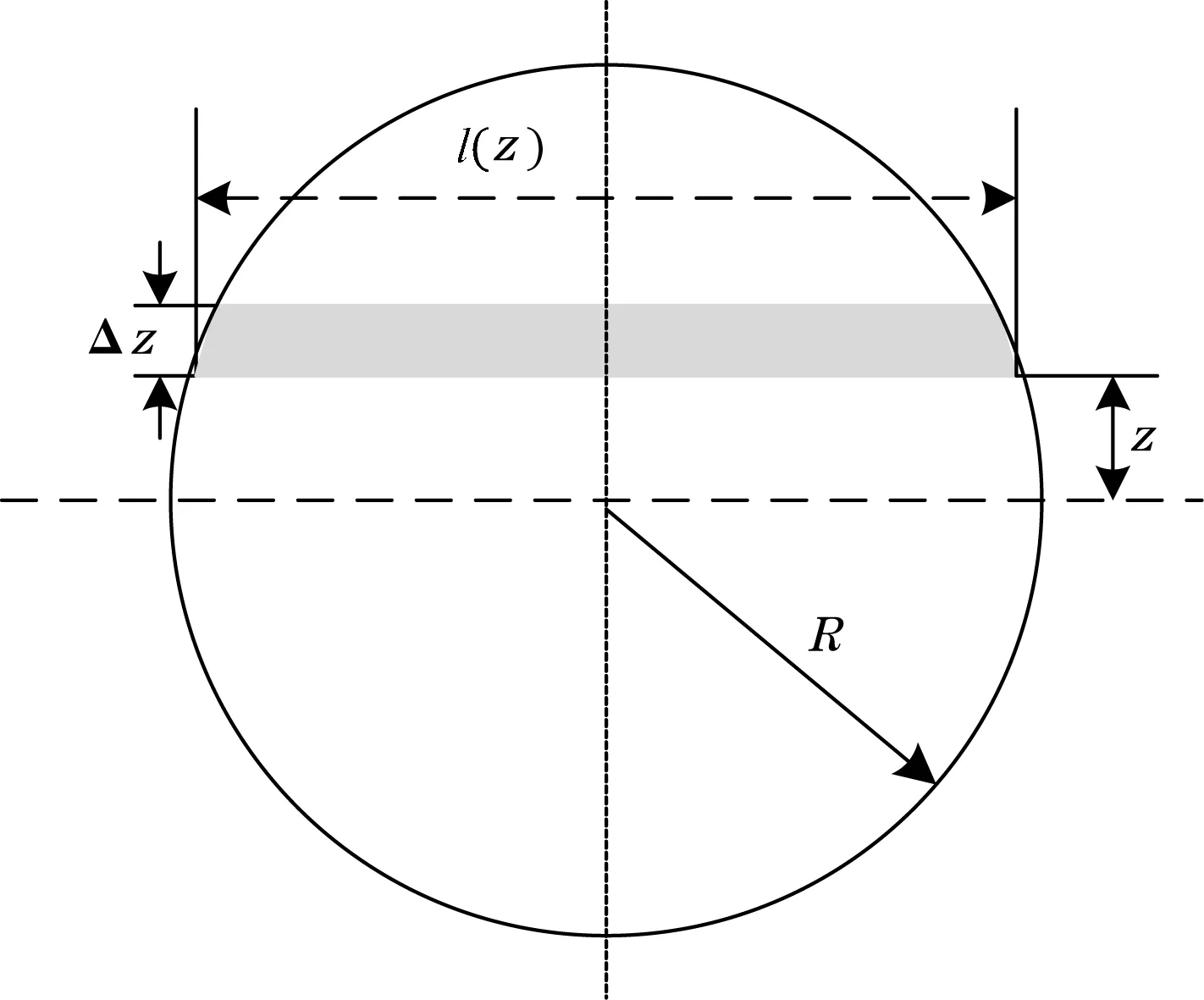
图2 圆形管道积分方法示意图
令α=z/R,则式(7)可改写为
(10)
式中vmi为相对高度αi处的流体流速。
(11)
综合式(10)和式(11),得:
(12)
式中ωi为声道i所对应的权重系数。
多声道超声波流量计布局及积分权重系数方案有很多种,目前国际上比较通用的有高斯-勒让德(Gauss-Legendre)、切比雪夫(Tchebychev),泰勒(Tailored)和圆管最优权重积分(OWICS)4种方案[13]。这4种方案都分别规定了声平面的位置zi/R和每个声道的权重系数ωi。经过综合对比,本文针对圆管流量测量的特点,选择OWICS方法进行声道布置,计算得到4声道超声波流量计的相对声路高度和权重系数如表1所示。

表1 OWICS积分法相对声路高度和权重系数
1.3 基于遗忘因子最小二乘法的权重系数计算
在流体的非理想流动状态下,根据上述4种积分方法进行声道布局和设置积分权重系数,会在测量中引入系统误差,降低测量精度。式(6)所示的多声道超声波流量计积分公式表明该积分过程是一种线性组合过程,测量方差可表示为[14-15]
(13)
权重系数ωi的选择依据是使式(13)所示的方差最小。为求取式(13)所示的线性函数的最优权重系数,本文引入带遗忘因子的递推最小二乘法进行在线计算和迭代更新,对不同测量位置的权重积分进行优化,实现在不改变声路高度的前提下,进行非理想流动状态下流体的流量测量。
在最小二乘法求解权重系数中,式(12)中的等式改写为
y(k)=φT(k)θ(k)
(14)
(15)
φ(k)=[ω1ω2…ωn]T
(16)
θ(k)=[vm1vm2…vmn]T
(17)
带遗忘因子的递推公式为
(18)
式中:λ为遗忘因子;K(k)为增益矩阵;P(k)为协方差矩阵。
在权重系数优化过程中,利用带遗忘因子的最小二乘法的迭代更新方式适用于在线计算和实时显示权重系数,可以实时绘制权重系数曲线,省去数据采集和离线优化的繁琐步骤。
2 管道模型及实验方法
2.1 几何模型的建立
以图3中的T型管和变径管两种管道模型为例,分析上游阻流件产生的涡流及扰流可能会对超声波流量计的检测精度造成影响。管道直径D=50 mm,变径管道最小处直径d=40 mm,上游缓冲管道长度为10D,出口管道长度20D。根据工业安装手册要求,下游缓冲管道长度需要大于10D,因此将超声波流量计设置在T型管或变径管不同位置处以分析缓冲管道长度对于流量计测量精度的影响[16]。
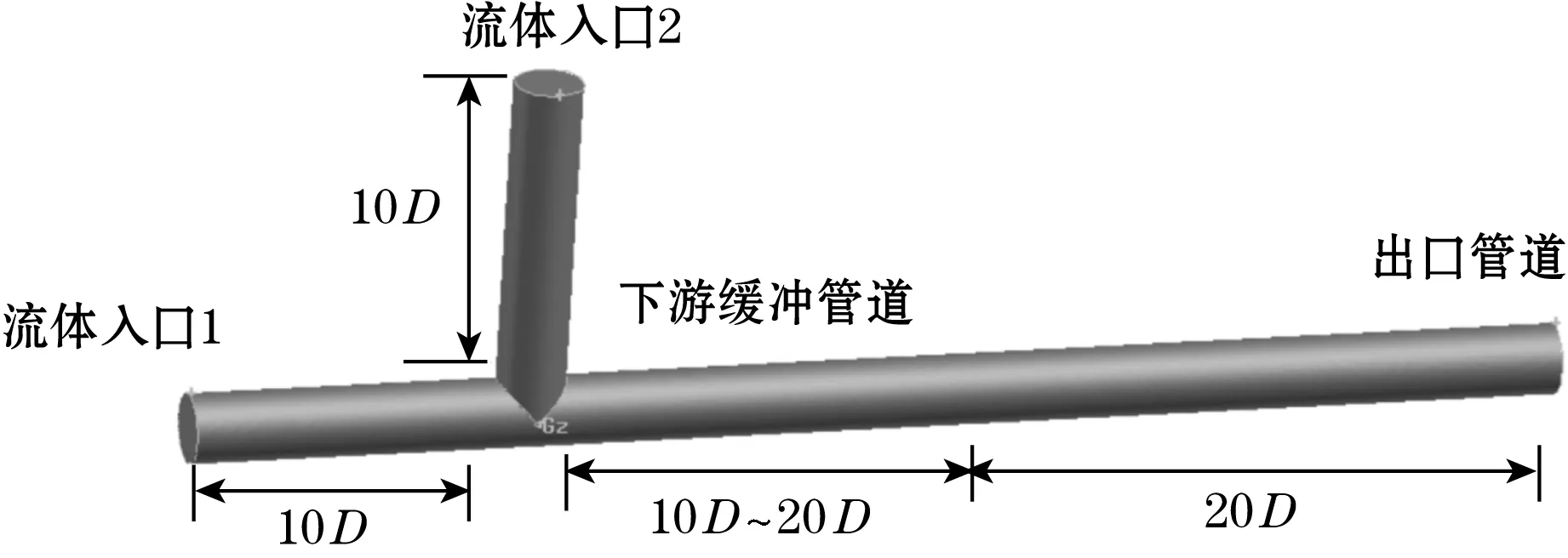
(a)T型管模型
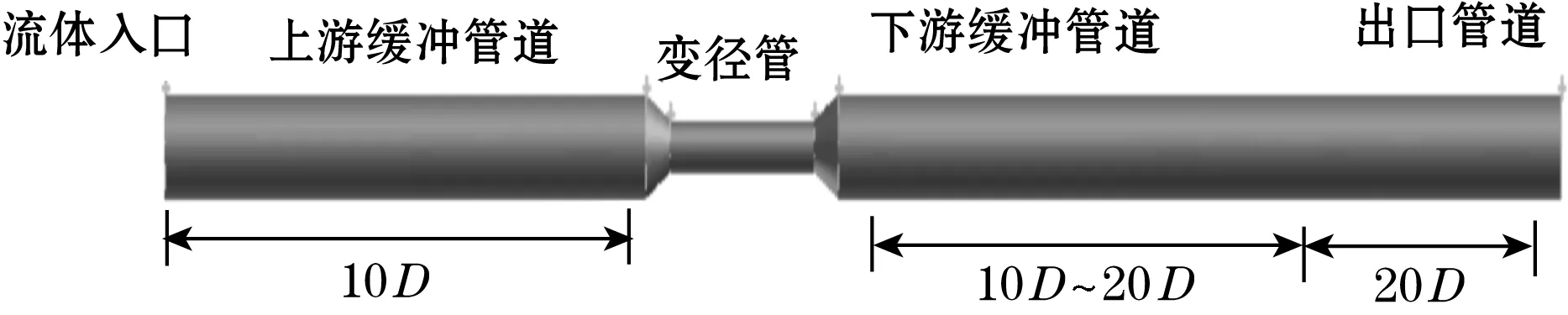
(b)变径管模型图3 管道模型示意图
2.2 FLUENT仿真设置
通过ICEM-CFD软件进行模型的网格划分,对T型管道交汇处、管道直径突变处进行局部网格加密,在流体进口处、管道壁面设置边界层网格,网格划分完成后总数量约为53万。管道内基础流动介质为戊烷(n-pentane-liquid),并根据需要调整流体的黏度;当雷诺数低于2 000时采用Lamina层流模型,当流体处于湍流状态时选择RNG k-ε湍流模型进行分析[17]。
网格划分完成后需进行网格无关性验证,以保证仿真实验的准确性。改变管道入口流速,分析网格总数约为30万、53万和75万模型下仿真结果的差异。发现网格数量在53万和75万时,计算结果随网格密度变化的敏感性很低,说明选择网格总数为53万的计算模型可以满足实验需求,由于本文篇幅的限制在此不再详细介绍分析过程。
2.3 实验装置及方法
实验中以24 ℃下黏度为2.3 mPa·s的煤油作为基础实验介质,为获取不同黏度的流体,用24 ℃下黏度为12.4 mPa·s的高黏度大庆油田原油与煤油按不同比例混合,得到黏度为4.1、6.4、8.3 mPa·s的3种黏度流体,并用密度计对4种介质密度进行测量[18]。
图4为超声波流量计检测实验系统,由水槽、计算机、标准管段、测试管段以及水循环泵等组成,配有温度、压力传感器,可以实现检测校准实验和运行环境监控。

图4 实验装置
在仿真结果的基础上,利用图4所示的实验系统对多声道超声波流量计的测量精度进行校准实验。多声道超声波流量计的声道数为4,共有4个声平面,声道安装位置按照表1数据进行设置,声平面与水平面平行。在实验中,流体流速每增加0.2 m/s为1档,从0~2 m/s依次递增进行测量。每次测量采集数据100组,用不同算法的权重系数计算流量,与标准表进行对比。
在T型管阻流件后10D处和变径管阻流件后10D处安装超声波流量计,其经遗忘因子最小二乘法优化后的权重系数如表2所示。
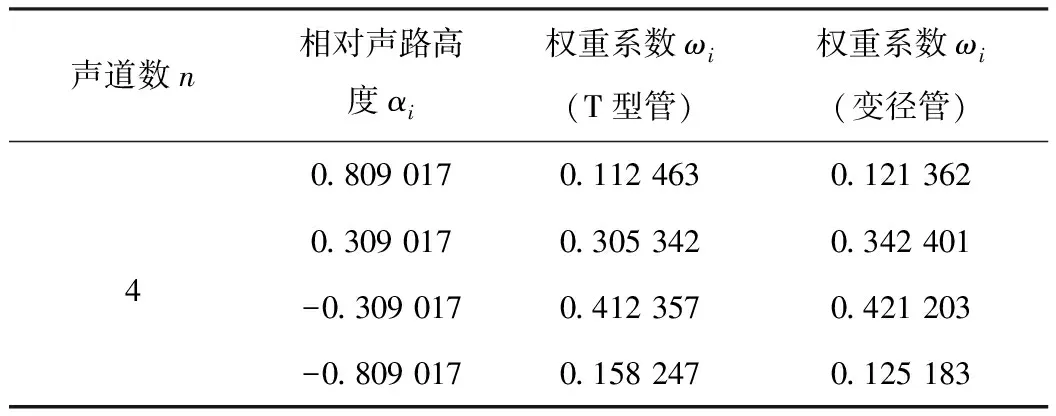
表2 遗忘因子最小二乘法优化的权重系数
3 结果讨论
3.1 流型分析
图5为T型管、变径管下游10D处管道内流体速度分布。固定入口流速为1 m/s,流体黏度设定为从6.4 mPa·s至2.3 mPa·s变化,对应雷诺数在6 718~18 695范围内。根据模拟结果可以看出,上游管道阻流件的存在使管道内流体流型出现非均匀分布情况;另外,随着流体黏度的变化导致速度梯度也会产生相应的改变。

(a)T型管,6.4 mPa·s

(b)T型管,2.3 mPa·s

(c)变径管,6.4 mPa·s

(d)变径管,2.3 mPa·s
对于T型管模型,两股进口流体的交汇处湍动程度较高,产生的涡流导致流速最高区域下移,而且随着流体黏度的降低其雷诺数相应增长,管道内扰动现象有所提高,速度梯度更加明显。
在变径管中,管道尺寸的突变造成了截面处流体形状的不规则分布,流场中存在部分区域流速低于入口速度,随着流体黏度降低,管道内流动惯性更加显著,但由于变径管结构下使流体流动方向被强行改变,进一步增强了流体的湍动程度,提高了管道截面处流速的最大值。
3.2 安装位置对流量计测量精度的影响
在管道运输中,超声波流量计的安装位置需要与上游阻流件间隔一定距离以保证流体充分发展,通常认为至少在30D以上才能避免流体湍动引起的测量误差。而在实际应用中,由于现场条件的限制,流量计大多安装在距上游管道10D外的位置,此时流体流动产生的误差已不可忽略,而采用带遗忘因子的最小二乘法的计算方法对积分权重系数进行优化,可以有效降低测量误差。
采用相对误差ε来定量描述不同安装位置、不同权重计算方法产生的影响,其计算公式如下:
(19)
式中:vl为采用最小二乘法计算得到的管道内流体平均流速,m/s;vm为流体流过管道截面的实际速度,m/s。
图6为上游管道为T型管时,采用传统积分方法以及最小二乘法在10D和20D安装位置处测量误差的变化。流体入口流速设定为0.2~1.4 m/s,对应雷诺数变化范围是3.7×103~2.6×104。从图6中可以明显看到,随着流体流速的提高流量计测量误差整体呈下降趋势,当流量计安装位置在10D时,传统积分方法的测量误差在±0.8%范围内,而采用最小二乘法优化的权重系数可以将测量误差控制在±0.3%以内;当流量计安装位置延伸至20D后,两种积分方法对应的测量误差最大值分别是0.51%和0.18%。
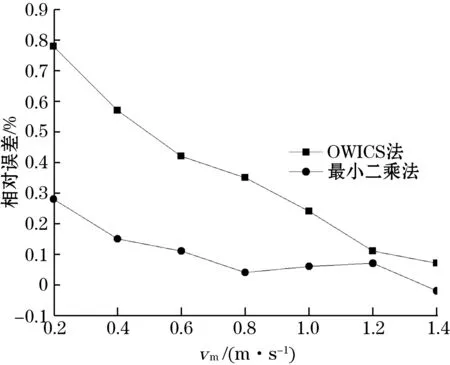
(a)10D

(b)20D图6 T型管下游不同位置处测量误差
图7为变径管下两种积分方法的测量误差,由于在相同位置处,流体在变径管下比T型管下湍动程度要高,当流量计安装位置在10D和20D时,传统方法的测量误差分别是±1.0%和±0.8%,高于T型管的误差范围。
此时采用带遗忘因子的最小二乘法的权重系数优化方法的优势更加明显,相同安装位置处对应误差范围均在±0.3%以内,说明即使超声波流量计无法安装在充分发展流管道内,采用此方法仍可以得到较精确的测量值。
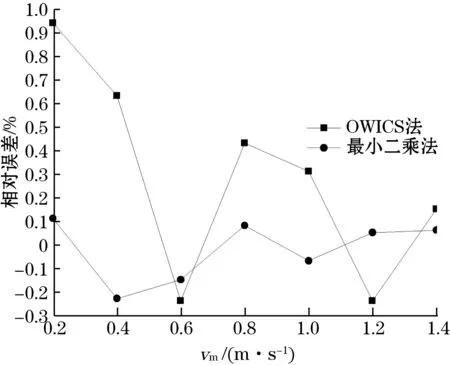
(a)10D
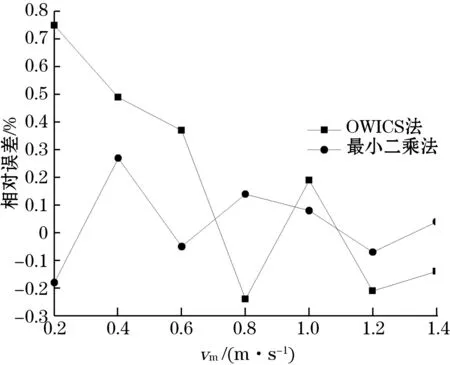
(b)20D图7 变径管下游不同位置处测量误差
3.3 黏度对流量计测量精度的影响
在阻流件下游15D处,相对误差绝对值与管道内流体流量、黏度的对应关系如图8所示。
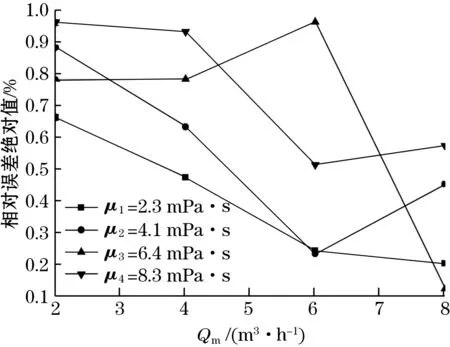
图8 T型管下不同黏度测量误差
从图8可以看出,提高流体流量能够有效降低流量计的测量误差,当入口流量达到8 m3/h后,相对误差最大值仅有0.54%;相同流速条件下,测量误差相对增长均保持在1.0%以下。
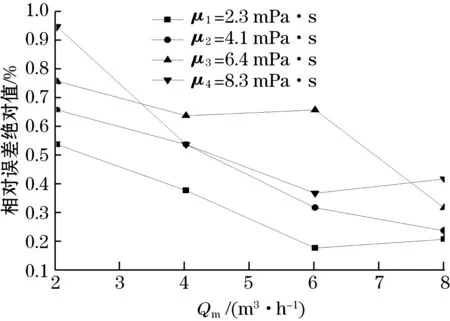
图9 变径管下不同黏度测量误差
图9为变径管下不同黏度测量误差。同样表明在变径管下所提方法能够有效降低流量计的测量误差,当入口流量达到8 m3/h后,相对误差最大值仅有0.42%,说明总体上采用遗忘因子最小二乘法的优化算法适用于不同种类的油品运输检测。
4 结论
针对当前利用多声道超声波流量计测量高黏度非理想流体的实际需求,提出了一种基于带遗忘因子的最小二乘法的权重系数优化方法。通过FLUENT仿真模拟方法,考察了上游阻流件为T型管、变径管下管道截面处流体速度场的变化情况;并根据实验测试分析了超声波流量计在阻流件下游10D、20D的安装位置以及不同黏度流体介质下测量值相对误差的变化情况。
结果表明,管道结构或流体物性的改变会对流体流型造成较大影响,随着介质黏度降低,管道截面处流体速度梯度会更加明显;当超声波流量计安装在阻流件下游10D位置处时,相比于OWICS积分法,采用遗忘因子最小二乘法优化权重系数测量得到的相对误差均能控制在±0.3%内,保证了即使工控条件对下游管道长度有约束,也能得到较精确的测量值;而且对于不同黏度的流体,此优化方法同样适用,入口流量在2~8 m3/h范围内测量的相对误差幅值最高只有0.95%,说明本文算法可以满足了炼油厂、加油站等企业对于不同物性油品运输检测精度的需求。

