直动从动件平面移动凸轮机构的动力学优化设计*
朱育权,李大印,尚涵涵
(西安工业大学 机电工程学院,西安 710021)
凸轮机构组成部分包括凸轮、从动件和机架,被广泛应用于机械领域。其中凸轮通过与从动件进行高副接触,使其获得各种形式的预期运动,凸轮机构的优化设计主要是对凸轮的轮廓曲线进行改造优化,传统的凸轮因自身的局限性往往不能实现预期的功能,因此引发了设计者们纷纷对其结构形式进行改造以达到预期效果。传统凸轮机构通过演化和变异形成一种具有新功能和运动形式的新型凸轮机构,其演变方式主要是在原始凸轮机构的基础上,对该机构的各个组成部分进行重新设计或改造。对于凸轮曲线设计方法,除了传统的设计方法外,还出现了一些新型设计方法。为了保证凸轮机构从动件位移曲线的连续性,要求凸轮轮廓曲线至少采用二次曲线[1]。文献[2]对构建正弦加速度修正梯形曲线的过程进行了分析。文献[3]采用几段高次多项式曲线拼接成的样条曲线作为凸轮轮廓曲线函数,以达到减小机构运动学参数峰值的目的。高次多项式样条曲线函数被作为凸轮机构从动件位移曲线函数,可以更有效地减小从动件加速度和从动件驱动阻力的峰值[4-5]。文献[6]提出了一种分数多项式模式。不同于传统方式中多项式指数为整数的现象,而是以分数代替整数作为多项式指数。这种方法可以有效的降低从动件加速度的峰值。文献[7]提出的运动函数具有正负加速度可调节的特征。这种方法设计出来的轮廓曲线适用从动轮和多腔凸轮,尤其适用于高速凸轮。其优点是允许设计者设置加速度的上限与下限,以达到设计目标。文献[8]提出了一种利用光滑样条曲线设计柔性凸轮轮廓曲线的方法。其优点在于设计者可以对凸轮进行局部修改,且凸轮轮廓线的平滑性和约束条件也得到了保证。
在凸轮设计过程中,设计者需要使凸轮机构的从动件达到目标行程,并将机构的运动或动力学参数控制在合理范围内,尤其在高速凸轮中,一些参数的设计指标要求更高。基于平面移动凸轮机构设计中存在的约束条件,本文以目标行程的约束和降低从动件驱动阻力峰值为优化目标,控制凸轮机构的最大压力角,保持凸轮机构凸轮结构总体尺寸不变,对凸轮轮廓曲线进行优化设计,通过仿真对优化方法的可行性进行了验证,为移动凸轮机构的设计提供了一种新的方法。
1 移动凸轮机构优化设计数学模型
直动从动件移动凸轮机构如图1所示。在图1中,vx为凸轮滑块速度,vy为从动杆件速度,l为滑块长度,f(x)为从动件的位移规律即从动件的位移函数,与滑块接触线的形状有关。x为凸轮滑块的位移。直动从动件与从动杆件固连,沿xOy坐标系的y轴方向做往复直线进给运动。
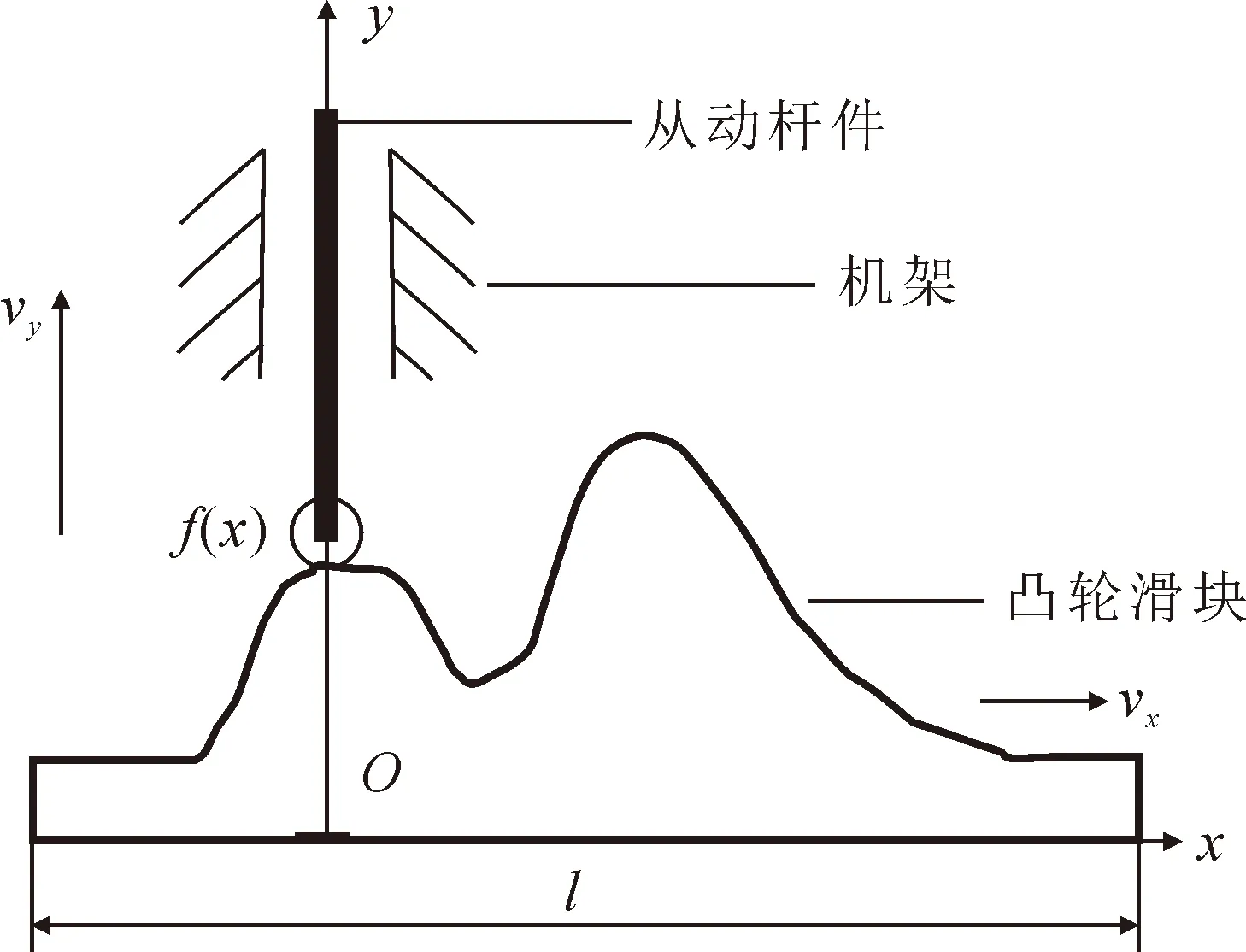
图1 直动从动件移动凸轮示意图
凸轮轮廓曲线是根据从动件位移规律设计出来的,可得
(1)
式中:h为从动件位移;Ci为多次项系数;n为项数。通常情况下,移动凸轮机构的滑块沿x轴做往复匀速直线运动,则滑块往返一次所用时间即从动件的运动周期为
(2)
结合式(1)、式(2)可得
(3)
式中:h(t)为从动件位移;t为时间。实际上在一些变异移动凸轮机构中,为了同时保证从动件应有的运动规律与相关零件的形状,图1中的滑块往往不是做匀速直线运动,而是在x轴和y轴均做各自相应的运动。则其各自关于时间t的函数表达式为
Z=z(t)
(4)
U=h(t)
(5)
式中:Z为滑块沿y轴的位移;U为滑块沿x轴匀速运动时的位移。最终从动件运动规律的位移表达式H(t)是滑块匀速运动下从动件的位移函数与滑块自身运动时在y轴方向上的位移函数z(t)迭加而成,即
H(t)=h(t)+z(t)
(6)
从动件的行程为
S=Hmax-Hmin
(7)
式中:Hmax为从动件位移的最大值;Hmin为从动件位移最小值。
从动件的速度为
(8)
从动件的加速度为
(9)
维持从动件运动所需的最小力称为驱动阻力,记为J,具体为
J=-ma
(10)
其中m为从动件的总质量。要改善移动凸轮的动力学性能,关键在于降低从动件驱动阻力的峰值Jmax。移动凸轮机构往往会存在从动件驱动阻力峰值过大的情况,甚至会在某些曲率变化点处发生力的突变。
曲线上任意一点N处压力角的几何示意图如图2所示。α为凸轮机构压力角。k为N点处切线斜率。n为样条曲线N点处的法线,e为从动件速度方向所在的直线。

图2 曲线上任意一点处压力角示意图
由图2可以看出,曲线上任意一点N处压力角α为该点处的法线n与直线e所夹的锐角。则压力角可表示为
(11)
在凸轮机构的优化设计中,须考虑其中一个重要参数即压力角。凸轮机构的压力角与轮廓曲线的斜率有关[9-13]。当机构取得最大压力角时,从动件与凸轮滑块的接触点N为轮廓曲线斜率最大点,将此点定义为控制点。将控制点处定义为轮廓曲线的原点时,可以减小参数设计时的计算量,此时从动件位移表达式中常数项C0=0、一次项系数C1=tanαmax,αmax为最大压力角。
滑块传递给从动件的接触力的方向在直线e上,传递给从动件运动方向的有效分力为
F1=Fcosα
(12)
其中F为滑块传递给从动件的接触力。在同等条件下,压力角α大小与有效分力F1大小成反比,同驱动阻力大小成正比。压力角α越大,则驱动阻力越大。但是过小的压力角又会造成从动件接触部分的过度磨损。凸轮轮廓上的压力角随位置的改变而改变。最大压力角αmax小于临界压力角αc是确保凸轮机构的正常运行的必要条件。现实的生产过程中,通常规定凸轮机构压力角的最大值αmax应小于压力角的某一许用值,其目的是提高机构的效率并改善机构的受力情况。一般情况下许用压力角要比临界压力角的值小的多。根据实际经验,在推动过程中,直动推杆的压力角许用值设定为30°,摆动推杆的压力角许用值设定为35°~45°。在返回行程中,促使推杆运动的力是封闭的。不会产生自锁现象,故压力角的值一般取70°~80°。因此设计者需要根据工程需求在合理范围内选择最大压力角。
通过上述几个主要运动动力参数的表达式可以看出,当从动件位于位移最大点hmax处时,从动件速度为0,驱动阻力达到峰值。此时,将从动件与轮廓曲线的接触点的横坐标定义为xm。
综上所述,将移动凸轮机构的动力学优化问题转化为单目标、多约束的优化问题,其目标函数为
(13)
其中αmin为最小压力角。
约束条件[14-19]为
(14)
式中:S0为凸轮机构的目标行程;l0为轮廓曲线的理论要求长度;α0为压力角的许用最大值;xe为轮廓曲线端点的横坐标;αxm为从动件与轮廓曲线的接触点处的压力角;αxe为轮廓曲线端点处的压力角。
2 仿真分析
以渔线轮装置中的凸轮机构为例,利用上述方法对该凸轮机构进行具体分析及动力学仿真实验。图3为该移动凸轮机构运动原理示意图。其整个机构运动方式如下:凸轮盘绕轮盘中心做圆周运动,相当于给凸轮盘添加一个转动驱动;直动从动件与凸轮曲线槽固连,轮盘上有一固定点,该点与凸轮曲线形成了凸轮副;直动从动件沿垂直方向做移动,相当于在从动件上施加了一个移动副。

图3 凸轮机构示意简图
在原通用模型内的滑块被滑槽与凸轮盘共同组成的驱动机构所取代,滑槽形状是基于凸轮廓线设计的。将圆柱销用质点P表示,凸轮盘中心用圆心O点表示。圆柱销到凸轮盘中心的距离即为质点P到圆心O的距离。将滑槽简化成样条曲线Spline,如图4所示,建立该机构的运动简图。图4中,R为质点P到圆心O的距离,M点为Spline的中点,θ为线段OP与从动件速度方向所在直线所构成的夹角。轮盘沿逆时针方向做圆周运动,角速度为ω。圆柱销(质点P)在沿轮盘做圆周运动的同时也沿着Spline的轨迹做往复运动,从动杆的运动是沿着竖直方向上下移动,如图4所示。从动杆件的运动速度用v来表示。质点P的位置与θ有关。设定质点P运动至Spline的中点即M点位置时,且圆心O位于M点下方,θ为0°;反之θ为180°。
在该装置中,从动件做直线往复运动,驱动为转动驱动。从动件的位移运动规律保证平稳完成推程和回程且只能有一个最大值,从动件在一个周期内位移规律的无因次图像形状如图5所示。
当运动至某一角度时,从动杆的位移与质点P的位置以及Spline中点M的位置有关。通过计算M点的位置坐标以及质点P的纵坐标对二者进行迭加即为从动杆的位移。以O点为原点建立x1Oy1坐标系。以M点为原点建立x2My2坐标系,如图6所示。
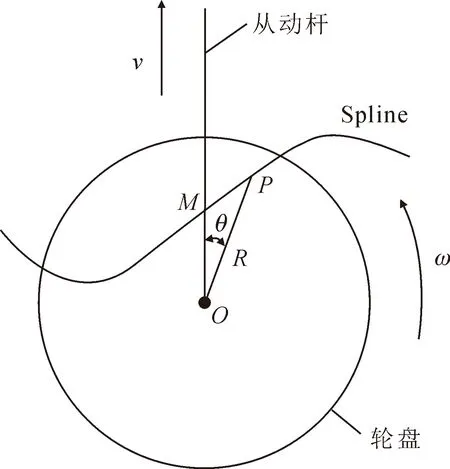
图4 滑槽凸轮机构运动简图

图5 无因次从动件位移运动规律图
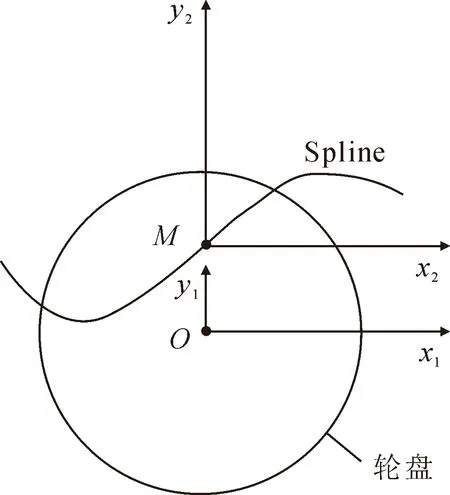
图6 坐标系定义图
基于x1Oy1坐标系,对任意转角θ下P点的位置进行求解。当转角θ的值为0°或180°时,与其对应的P点的纵坐标y1值为R或-R。凸轮盘绕轮盘中心沿逆时针方向做圆周运动,则P点的位移表达式为
y1=Rcosθ
(15)
设在x2My2坐标系中,Spline曲线方程为y2=f(x2)。其中在任意转角θ下,P点的横坐标为
x2=-Rsinθ
(16)
根据凸轮机构运动原理,从动杆是沿着线段OM的方向做直线运动。当质点P移动至M点位置时,此时θ=0或θ=180°且y2=0。从动杆的总位移为
s=y1-y2
(17)
由于滑块的形状与总体尺寸限制,其轮廓曲线设计成“S”形,结合从动件运动规律的约束,故采用三次多项式样条曲线[20-25]。可得从动杆总位移为
s=Rcosθ-c(Rsinθ)3-bRsinθ
(18)
其中c、b为系数。取样条曲线控制点数为n,压力角控制点Ni(i=1,2,…,n)定义如图7所示,E和A分别为样条曲线的两侧端点,样条曲线Ni点处,均存在独立的斜率及相应压力角。以M点为原点建立坐标系,保证控制点M的压力角是整个样条曲线最大压力角。

图7 压力角控制点定义图
样条曲线关于M点对称,驱动阻力的正负值为一对相反数,只需控制正值最大值为最小,则相应的目标函数为
minJθ1=min(mRcosθ+6mcR3sinθcos2θ-3mcR3sin3θ-mbRsinθ)
(19)
式中:θ1为位移最大处的转角;Jθ1为在θ1处取得的最大驱动阻力。约束条件为
(20)
式中:θ2为从动件处于最低位移时所对应的转角;R0为销到凸轮盘距离原始值。
根据遗传算法的计算原理,当目标函数始终为正值时,适应度函数即为目标函数本身,故该机构中的目标函数为适应度函数[26-27]。其优化变量有4个,即样条曲线三次项系数、一次项系数、最大位移处对应转角和圆柱销距轮盘中心距离。初始种群数量设置为50个,为了保证种群的多样性,遗传算法中包含了变异、交叉和选择三种操作。最优适应值关于遗传代数的图像如图8所示。

图8 遗传算法最优适应值与遗传代数的函数图像
轮廓曲线三次样条曲线表达式为
(21)
对应的R=5.9 mm,图9为优化后从动件一个周期内的位移规律图像,符合预期要求的从动件运动规律。
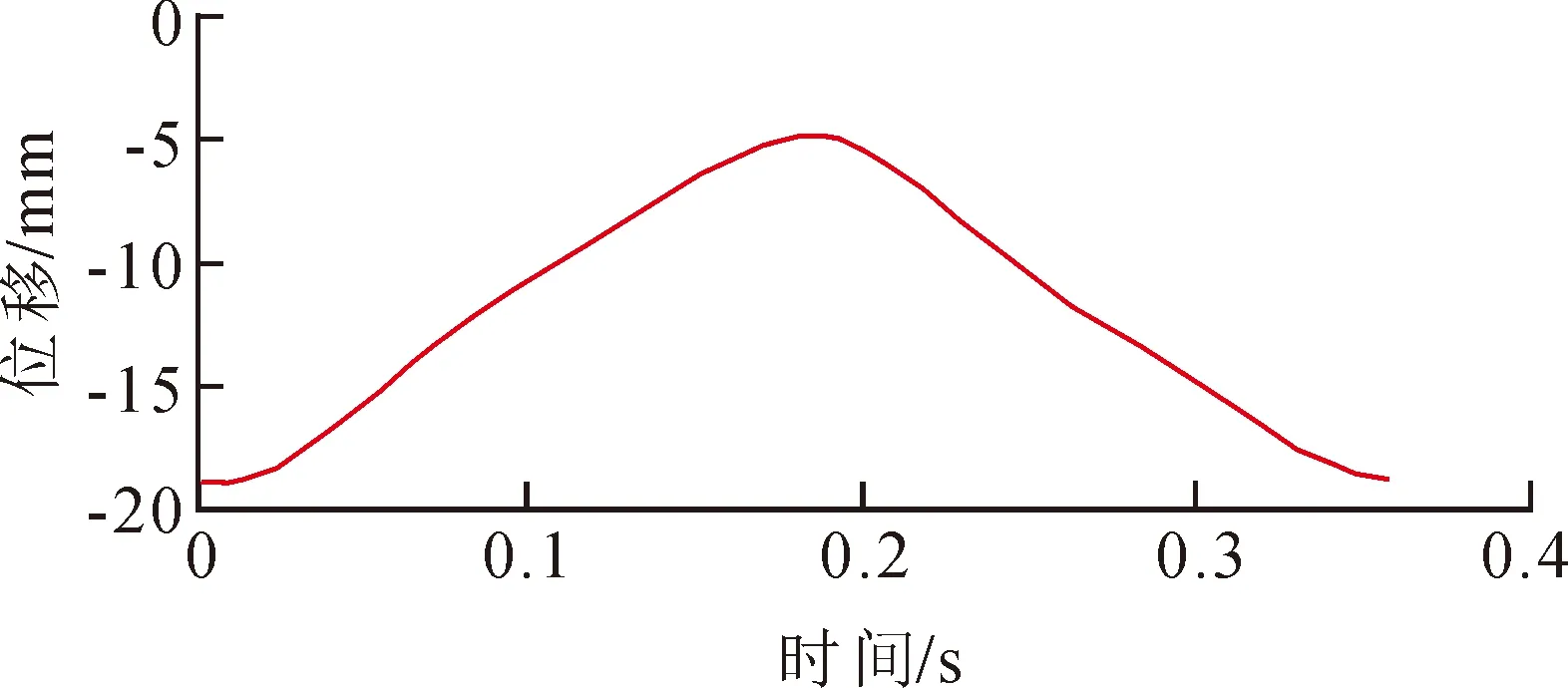
图9 优化后一周期内从动件运动规律图像
图10是优化前后驱动阻力的对比情况,从中可以看出优化后的轮廓曲线所对应的驱动阻力变化更为平缓。

图10 优化前后一周期内驱动阻力对比图像
表1以数据的形式反映了优化前后机构各参数的对比情况。

表1 优化前后参数对比
通过优化前后各个参数之间的对比可以看出:优化前后行程S变动量为0.077 mm,基本保持稳定。满足了1 mm最大行程变动量的工程需求。最大驱动阻力由优化前的0.567 N减小到优化后的0.348 N。且驱动阻力波动值也由优化前的1.133 N减小到优化后的0.696 N。其波动趋势更加平稳。
基于上述优化步骤,销和凸轮轮盘的中心距离以及样条曲线的表达式可根据压力角和目标行程确定。需要根据工程需求在合理范围内选择最大压力角。经过理论推导和仿真试验,证实了优化方案的可行性。
3 结 论
1) 建立了直动从动件平面移动凸轮机构的优化数学模型,对凸轮轮廓曲线形状进行了优化设计。销和凸轮轮盘的中心距离以及样条曲线解析式由压力角和目标行程确定。
2) 对优化后的移动凸轮机构动力学特性进行仿真分析,结果表明优化后机构的最大压力角减小了10.31°,最大驱动阻力下降了38.5%,验证了移动凸轮机构优化设计方法的可行性。

