为什么除法竖式不一样*
——兼谈竖式的记录功能及不同形式
章勤琼 唐 娟
笔算与竖式一直是小学数学的必学内容,有人认为,应该特别强调笔算方法及其规范性,因为笔算不仅是运算的书面记录,与运算的过程也是对应的,可以间接看成是运算法则的直观化。在数学学习过程中,笔算的重要地位取决于它的“精致性”和“严密性”。但也有人认为,“过去,对传统的笔算方法的精通程度一直是衡量学生对数学掌握程度的标准,这样的观点现在再也站不住脚了。事实上,对脱离具体情境的传统笔算方法进行过度训练反而会阻碍学校数学课程标准中整体目标的实现。”[1]
在加减乘除四则运算的竖式中,除法竖式在形式上与其他竖式运算不同,对很多小学生来说,掌握起来并不容易。不少学生最早接触除法竖式时,并不理解除法竖式每一步所代表的意义,甚至可能会出现如图1这样错误迁移的例子。
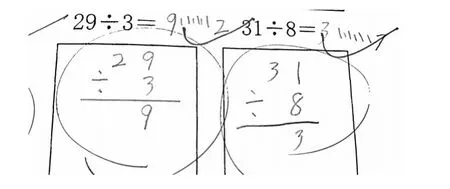
图1
那么,跟除法竖式相关的数学概念有哪些,该如何帮助学生理解并掌握除法竖式呢?我们应该对其相关数学概念进行梳理,进而对教学有进一步的思考。
一、除法竖式与计算过程的对应
笔算是常用的计算方法之一,指的是用笔书写演算过程的计算方法。笔算要求写出竖式,计算时有严格、固定的顺序,有明确的计算法则。[2]竖式是笔算的一种书写方式,可作为横式的说明或补充。[3]在小学数学教材中没有给出竖式的明确定义,但是在学习加法、减法、乘法、除法的笔算时,都出现了竖式,并且要求学生会用竖式进行计算。[4]
由此可以看出,竖式作为笔算的形式,其主要功能是记录计算的过程。以竖式记录的形式,要求有既定的格式,一般会将竖式计算的方法称作“标准算法”。但需要注意的是,“标准算法”并不是唯一的计算方式,在很多时候,学生自主使用的计算策略与标准算法并不一致。
首先,学生自主创造的计算策略通常是将要计算的数作为整体来处理的,而标准算法则是基于每一数位上的数字(0-9)进行计算。如在计算45+32时,对于十位上的计算,学生的自主计算策略会以“40+30”来代替“4+3”,而标准算法则是在十位上计算“4+3”。再如在计算618-254时,学生的自主计算策略可能是从600-200=400开始,另外一种可能的方法是将减254看成先减300,再加上46。无论哪种方法,都是把参与运算的数当作完整的数来看,而不是作为某一数位上的数字来考虑。
其次,学生自主创造的计算策略通常是从数的最高位开始的。比如在计算263+126的时候,一般都会从计算200+100=300开始。然而,标准的算法要从右边算起,先从计算“3+6=9”开始,需要遵循从最低位开始算的原理。只有除法的标准算法除外。
再次,标准算法一般会强调“一种正确的方法”,而学生自主创造的计算策略会具有更多的选择。因为自主创造的计算策略是依赖于具体数字的,因此学生可以根据不同的情况有更多的选择。譬如在计算465+230和526+98时,多数学生会使用不同的策略或方法。然而,标准算法则要求能用同样的工具和方法解决所有问题。[5]
从上面的论述可以看出,除法竖式作为唯一一种从最高位开始计算的标准笔算方法,与学生常用的自主计算策略顺序相同。然而,我们在教学除法竖式时,往往会从形式上有更多要求。比如当出示竖式4)583时,要求先从百位除起,用“5”除以4之后从“5”里减去1个4,剩下来的“1”再和掉下来的8一起组成18,继续除以4。这样的过程,对于很多学生来说并不容易理解,比如为什么可以直接忽略“83”而用“5”去除?
因此,在面对这个问题时,我们希望学生能将583理解成5个百、8个十和3个一。而不只是三个数位上的不同数字5、8和3。其中一种常用的方法是可以使用学生熟悉的情境,如10条能量棒可以捆成1盒,而10盒又可以装成1箱。可以给出这样一个问题:有5箱、8盒以及3条能量棒,现在需要平均分给4个学校,每个学校可以分到多少条能量棒?在这样一个情境中,学生容易理解,要先对能量棒以箱为单位进行平分直到不能再分,再将剩下的箱子拆开,与原有的盒子一起,以盒为单位进行平分,同样分到不能再分以后,再拆开和条合在一起,再以条为单位进行平分。[6]
除法的本质是不断地对不同单位的总数进行平分的过程,分了之后对剩余的进行转化,与下面的单位进行合并以后再重复这样的过程。这也解释了为什么除法竖式要和其他三种竖式的计算形式不一样,因为加法、减法和乘法都只涉及参与计算的两个数以及运算结果,但除法却还要涉及余数以及对余数的转化处理,因此必须要采取这种可以连续进行记录的方式。除法的计算过程其实就是要回答这么几个问题:分谁?分多少份?每份分多少?已分出去了多少?还余下多少?余下的怎么办?[7]为了回答这几个问题,在记录除法的计算过程中,需要包含4个关键的步骤:第一,平分并记录下每组获得的数量;第二,记录下已经分掉的数量的总和,这里的数量需要通过乘法来计算得出;第三,记录下还剩余部分的数量,这里需要通过减法来获得这个数量;第四,将剩余的部分继续转化为较小的单位,并与已有的较小单位进行合并,在下一栏记录下新的数量总和。[8]
这是除法意义的本质,也是在除法竖式中需要反映出来的过程。
二、除法竖式的不同形式
笔算除法的形式并不只有我们现在熟悉的这一种样子,历史上出现过许多现在看起来极其烦琐的计算方法。[9]中世纪欧洲流行的除法和现在就大不相同。其中,较通用的一种方法称为“帆船除法”或“勾画除法”。其算法是先将被除数与除数写下来,然后进行演算。在演算过程中随时将已处理完的数勾画掉。演算完毕,在沙盘或纸上留下一行又一行已划掉的数,好像一只帆船。以106704÷456为例,“帆船除法”的算法如图2所示,这种方法在欧洲盛行了300年以上。[10]
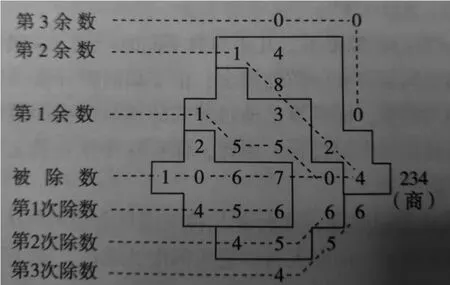
图2
“帆船除法”的记录过程过于复杂,早已被淘汰。现在我们经常使用的除法竖式记录方法称为“长除法”,但长除法也并不是只有一种形式。如图3所示的记录方法,并没有要求每一步都按照数位对齐一步除到位,而是分步骤来除。事实上,这与前面提到的记录除法过程的四个步骤是一致的。
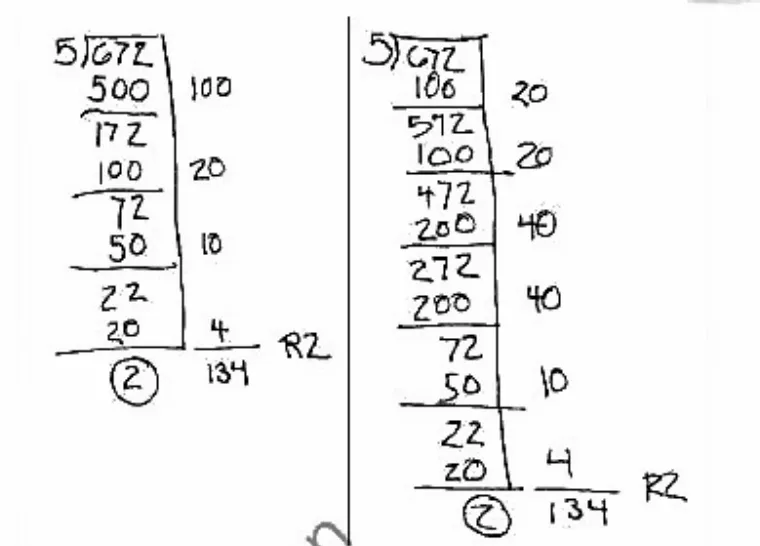
图3
事实上,标准的除法竖式也并非一定要采用一成不变的形式。考虑到除法竖式在形式上对不少学生来说存在困难,Van De Walle提出了另外一种称作“明确转化法(Explicit-Trade Method)”的除法竖式。如图4,跟标准算法的每一步“掉下来”的方法相比,“明确转化法”将每一步除不完的部分都先划去,经过“转化”以后再和下一个单位合在一起继续除,这个过程就和前面提到的那个能量棒的情境相通。相比而言,像这样的“明确转化法”对学生而言更容易理解。[11]
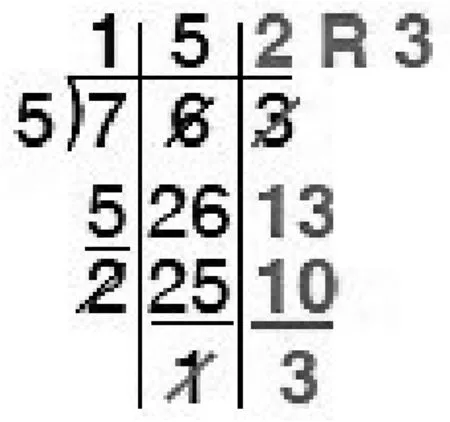
图4
如图5所示,与左边的标准竖式相比,通过“明确转化法”可以帮助学生更好地建立竖式与模型的联系,适当减轻他们的认知负荷,而在数位之间加上间隔的竖线,可以帮助他们更好地避免数位对不齐带来的错误,尤其是当商的中间数位上出现0的时候。
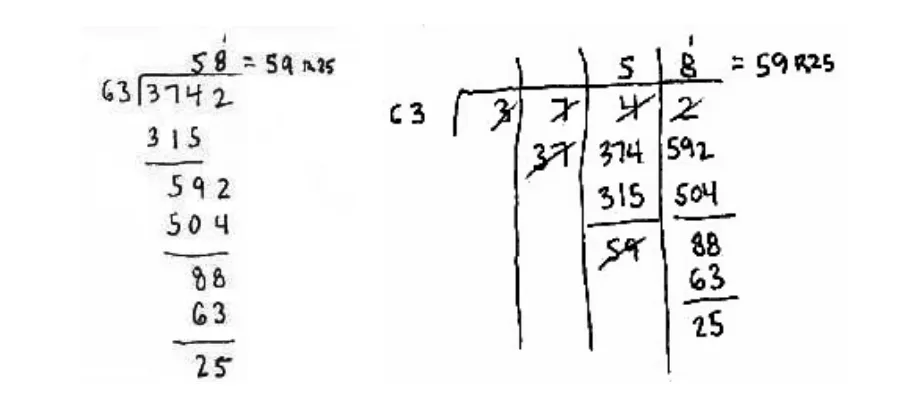
图5
还有一点需要特别指出的是,图5中,不论是标准竖式还是“明确转化法”,在试商的时候都采取将除数“63”往大估成70的方式,最后当发现个位的商太小的时候,并没有擦去原来的记录“8”,而是直接在上面写了“1”,最后在结果中加上1。像这样的记录方式,虽然看着不是十分规整干净,但却完整地记录了思维的过程,也减轻了学生试商的心算负担。
三、两点教学建议
第一,要加强对除法意义本质的理解,沟通心算策略与竖式的关联。我们期望所有学生最终都能使用有效的笔算方法进行计算。但是,只有循序渐进地建立这些方法,并不断地完善和扩展这些心算策略,笔算方法对学生来说才是有意义的。因此,只有让学生理解了除法的意义,并以除法的意义来促进他们对竖式中每一步过程的理解,才可能让学生真正掌握除法竖式的形式。[12]在有的数学教材中,在学习除法竖式的时候先学习有余数除法,再学习没有余数的除法竖式,[13]因为有余数的除法竖式的每一步能更好地与平分模型的计算过程对应起来。
第二,教学竖式时,应注重灵活性和规范性,以期达到学生自主创造的计算方法和标准算法的平衡。竖式的作用是记录计算的思考过程,减轻心算带来的认知负担。如果对竖式的要求在格式上过于严格,可能会造成学生在列竖式进行计算时仍然有比较沉重的心算负担。比如学生在学习笔算乘法时,在学了格子乘法的方法以后,[14]遇到比较复杂的三位数乘两位数(如379×78),不少学生喜欢画格子用格子乘法来做,而不喜欢用竖式。究其原因,在用竖式计算379×78时,要分别心算379×8和379×7,这对很多学生而言并不容易。而利用格子乘法,虽然记录的内容增加了,但每一步的计算都非常简单,只要能完成表内乘法和20以内加减并做好记录,就能解决。在除法竖式的教学中,也要思考如何更好地体现除法的计算过程,并通过记录来减轻学生的心算负担,而不是片面强调格式的统一性和规范性。
此外,不论使用的计算策略是心算、笔算还是使用计算器,其合理性取决于问题本身、所运用的数字以及计算的目的,教师需要培养学生灵活地选择合适的计算策略的技能。[15]


