解决问题策略的体验与感悟

黄海英

（江苏省启东市紫薇小学，江苏 南通 226200）

什么是策略？策略可以分为两类：一类是具有普遍意义的，常与一些数学思想方法紧密结合，如转化、画图、列表等，另一类是针对某一类典型问题总结出的带有规律性的策略，如一一列举、倒推、替换等。前者旨在形成解决问题的总体思路，而后者重在如何解决的具体对策。当然，这两个环节经常是彼此融合在一起的。那么“策略”到底可不可以教给学生？该怎么教？笔者试图根据认知策略的形成规律，结合五年级上册“解决问题的策略(一一列举)”一课，谈谈自己的教学实践与思考。

一、在操作中感知策略

瞧，王大叔家东面有一块空地，他想用18根1米长的栅栏围成一个长方形的花圃，有多少种不同的围法？（出示例1）

师：从中你得到了哪些有用的信息？

生：长方形的周长是18米。

师：你能用18根火柴棒代替栅栏试着围出一个长方形吗？看谁围得又对又快！注意要把18根火柴都用上。

学生尝试操作。

师：谁来说说，你围了一个怎样的长方形？（根据学生回答随机出示不同的围法）怎么想的呀？

生：周长是18米，那么长与宽的和就是9米。

师：你能把符合要求的长和宽都写出来吗？

教师巡视指导，收集代表性的作业。

生1：长方形的长（米）6 8 5 7

长方形的宽（米）3 1 4 2

生2：长方形的长（米）1 2 3 4

长方形的宽（米）8 7 6 5

生3：长方形的长（米）8 7 6 5

长方形的宽（米）1 2 3 4

师：看看这几位同学的作业单，你有什么想说的吗？比一比，你喜欢谁的方法，为什么？（板书：有条理）

师：像生3这样把符合要求的长和宽一个一个写出来，就叫做“一一列举”。有条理地一一列举是解决这个问题的基本策略。

王大叔想在这个花圃里种花，他会选择哪种长方形呢?我们来算算看，这几种长方形的面积分别是多少平方米？学生口算出每个长方形的面积。

长方形的长（米）8 7 6 5长方形的宽（米）1 2 3 4长方形的面积（平方米）8 14 18 20

师：仔细观察，比较它们的长、宽和面积，你还有什么发现？想一想，再和旁边的同学交流一下。

师：什么情况下面积最大？什么情况下面积最小？

生：周长不变时，长与宽越接近，面积就越大。

师：的确，“周长不变时，长与宽越接近，面积就越大”，这个规律可是一位著名的数学家在你们这么大的时候发现的，知道他是谁吗？（出示欧拉图片）

[思考]在教学解决问题的策略之前，学生已经解决过许多问题，初步积累了一些解决问题的知识和方法。过去的解题经历是形成策略的宝贵资源，形成策略需要学生的自主体验。围花圃，几乎每个学生都能说出一两种围法，但不容易说出一共有几种围法，更列不出算式。如果从能够说出的围法切入，依次把其他各种围法排列出来，问题自然就迎刃而解。把学生的无序列举作为教学资源很好地利用，与有序列举相比较，可以引起学生对两种不同列举形式优劣的思考，从而体会有序列举的价值。

二、在交流中建构策略

花圃围好了，王大叔要去购买花苗。有三种花苗可供选择：月季花、美人蕉、夜来香。“最少买1种花苗，最多买3种花苗”这句话是什么意思？

生：可以买1种，也可以买2种，也可以买3种。

师：一共有多少种不同的买法?你能试着用一一列举的策略解决这个问题吗？

教师巡视，收集不同的列举方法。

生4：3+3+1＝7（种）

生5：

月季花 月季花、美人蕉 月季花、美人蕉、夜来香美人蕉 美人蕉、夜来香夜来香 月季花、夜来香

展示交流，进一步追问：

你认为要得到全部答案，列举时要注意什么？（板书：不重复不遗漏）

师：大家的方法都不错，老师也来介绍一种。先画一张表格，把购买的方法分成三类：买一种、买两种、买三种。每一列就表示一种买法。

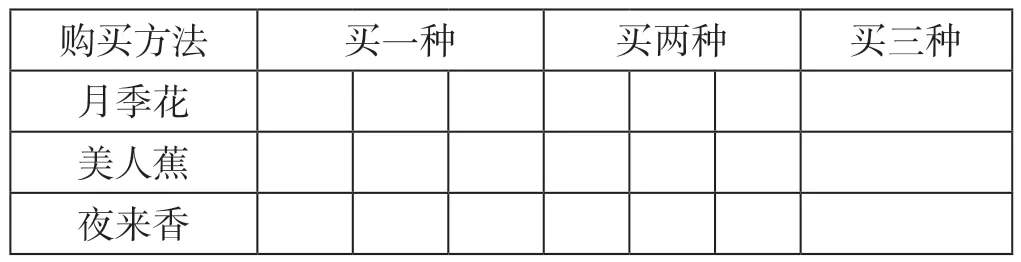
购买方法 买一种 买两种 买三种月季花美人蕉夜来香

你能用画√的方法表示出不同的买法吗？学生填表。

展示交流：

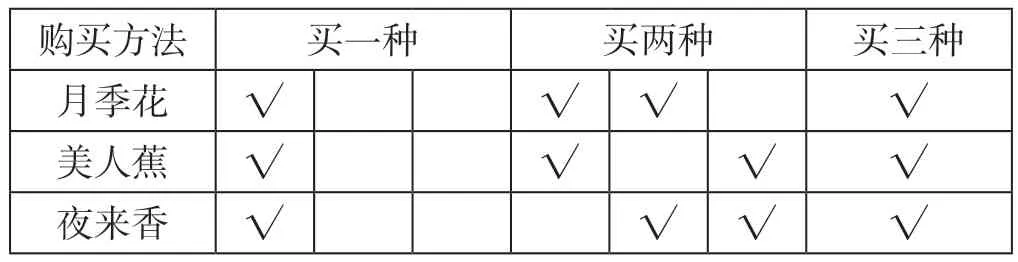
购买方法 买一种 买两种 买三种月季花 √ √ √ √美人蕉 √ √ √ √夜来香 √ √ √ √

师：这位同学的方法对吗？怎样打“√”才符合要求呢？

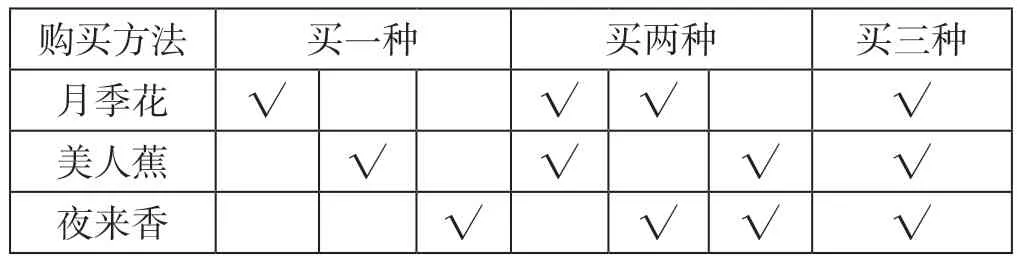
购买方法 买一种 买两种 买三种月季花 √ √ √ √美人蕉 √ √ √ √夜来香 √ √ √ √

师：这样有序思考表示得非常清楚，既没有重复也没有遗漏。

[思考]教材中的例2与例1大相径庭，在教学时我运用上面围花圃的素材导入到花圃围好后去购买花苗，这样情境创设更具有连贯性。本环节旨在让学生进一步体会解决问题策略的多样性，增强灵活选用策略的能力，促使学生多视角、多形式地解决问题。事实上，列表策略强调的是用表格呈现信息，一一列举策略强调的是列出所有可能的情况。用表格列出所有可能的情况只是一一列举策略的一种具体表现形式，这种形式能较清晰地列出所有的可能，但并不是唯一的形式。我们应该允许、鼓励学生选用适合自己的不同方式来表达对策略的理解。

三、在游戏中掌握策略

王大叔的问题解决了,他邀请我们来做个游戏。（出示游戏规则：一张靶纸共三圈，投中内圈得10环，投中中圈得8环，投中外圈的6环。如果投在两圈之间，就重来一次。）请一名男生和一名女生来试一试，其他同学来算他们一共得几环。

教师将靶面背对大家，让败方再投一次。师：他投中了两次，可能得到多少环？猜一猜，再把他可能得到的环数都写下来。

学生汇报算式，教师分同圈和不同圈两种情况板书。

师：投中两次，可能得到多少环？（12环、14环、16环、18环、20环）只看总环数，可能得到的环数有5种。

师：这个游戏我也玩过，不过我站得比较远，投了两次，你们猜猜我可能得到多少环？（板书：中1次 没中）

师：一字之差，却多出了四种可能，看来我们解决问题之前一定要认真审题！

[思考]游戏是学生最喜爱的学习方式，教师应该站在学生的立场上，以学生发展为本，既要吃透教材，又要敢于超越教材，设计出能点燃学生思维火花的教学环节，多给学生一些思考的时间和活动的空间，让每个学生都能在轻松愉快的氛围中解决问题，从而得到最大限度的发展。

四、在拓展中提升策略

师：一一列举能解决的问题数不胜数。我国古代有一部数学名著《孙子算经》，其中有这样一道有趣的题目《三女归家》：今有三女，长女五日一归，中女四日一归，少女三日一归。问三女何日相会？

师：你能读懂题目的意思吗？用一一列举的策略能解决这个问题吗？

从三人同一天走后算起，大女儿再回娘家要隔5天，二女儿再回娘家要隔4天，小女儿再回娘家要隔3天。

大女儿：5 10 15 20 25 30 35 40 45 50 55 60 65 70……二女儿：4 8 12 16 20 24 28 32 36 40 44 48 52 56 60……小女儿：3 6 9 12 15 18 21 24 27 30 33 36 39 42 45 48 51 54 57 60 65……

答：至少再隔60天三人再次相会。

师：今天我们用 “一一列举”的策略解决了这么多问题，你能说说在使用这种策略时要注意些什么呢？

小结：用一一列举的策略解决问题时，一般要先对各种方法进行分类，然后有条理地列举，做到不重复，不遗漏。

[思考]策略的丰富内涵是“镶嵌”在问题解决过程中的。只有在具体解决实际问题时，学生才能亲身实践如何把现实问题提炼、转化为数学问题，并在这一过程中全面理解数学策略的内涵。解决问题策略的教学，就是学生在解决问题过程中对策略的感悟和提升的过程，而策略的提升应与数学思想相贯通，并最终促进学生数学思维的发展。