圆柱型直通表冷器数字化设计模型

曾炜杰，谷 波，李强林

(上海交通大学 机械与动力工程学院，上海 200240)

组合式空调机组是中央空调系统的关键组成部分，集送风、冷却、加热、加湿、空气净化、消音等多种功能于一体.传统的组合式空调机组采用断面为矩形的结构形式，其换热设备基本上为平面翅片管换热器.

为了突破常规矩形断面空调机组冷凝水飞溅、过渡季节旁通困难等限制，现在已有企业开始生产断面为圆形的空气处理机组(圆筒式空调机组)，并投入到实际使用中.圆筒式空调机组具有节省空间、节电节能、运行噪声低等优势.为适应这种新型的特殊结构，圆筒式空调箱采用特制的圆柱型直通换热器.

对换热器而言，产品的开发、设计选型需要基于大量的性能试验，耗材费时，人力和时间成本较高.对换热器进行数学建模计算，实现换热器的数字化设计，不仅能缩短产品的开发、设计周期，同时能够对非常规工况、结构以及试验很难到达的工况进行设计计算，通用性强.关于翅片管换热器的计算模型研究已非常成熟：王强等[1]通过采用不同的传热、压降公式对不同风速分布下的翅片管换热器进行仿真分析，并与实验进行了比较验证；文献[2-5]中则建立了翅片管换热器的控制方程，对换热器进行数值模拟计算，藉此分析翅片管换热器的流动与换热特性.文献[6]中利用反传热分析方法建立了翅片管换热器的数学模型，并用于计算换热器的接触热阻.而针对圆柱型直通换热器的计算模型目前还没有相关研究，因此建立适合这种换热器的模型算法，无论对圆筒式空调箱企业的生产开发还是对这种新型换热器的推广使用都具有重要意义.本文以热力学、传热学理论为基础，基于与换热器结构特点契合的分排参数模型对圆柱型直通表冷器的结构设计进行建模计算.

1 模型建立

1.1 对象物理特征

圆柱型换热器，又称为圆柱型直通换热器，是具有空气直通功能、断面为圆形的圆柱状翅片管换热器，其三维结构如图1所示.换热器轴向方向是圆柱体的长度方向，断面是从内到外依次排布的同心圆弧换热管，翅片方向与圆弧管垂直.与传统平面翅片管换热器相比，圆柱型直通换热器的计算有以下不同点：

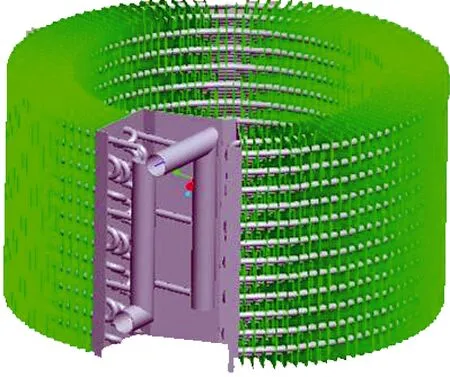
图1 圆柱型直通换热器Fig.1 Cylindrical straight-through heat exchanger

(1)作为换热对象的空气经过换热器的流向不相同；

(2)平面翅片管换热器各排换热管结构相同，而圆柱型直通换热器每一排管的结构参数不同；

圆柱型直通换热器的空气气流沿径向方向流过换热器，如图2所示.在空调季节，电动风阀关闭，气流通过垂直换热管的方向流经换热器进行换热；而在过渡季节，阀门打开，空气直接从圆柱体中间穿过，实现换热器的旁通.这种流路布置形式实现了换热器迎风面(圆柱体轴向)与空气进风面(圆柱体底面)分离.

确定圆柱型直通换热器的结构，需要如表1所示的基本结构参数.

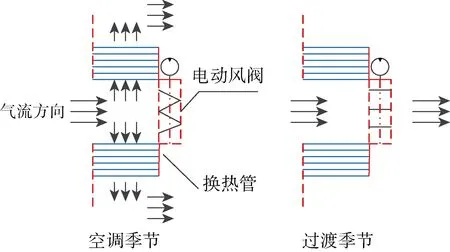
图2 圆柱型直通换热器气流组织示意图Fig.2 Air distribution of cylindrical straight-through heat exchanger

表1 基本结构参数Tab.1 Basic structure parameters

1.2 分排参数模型

作为空调机组的表冷器进行制冷时，换热管外为被处理的空气，管内走冷水.换热器运行时大多数处于稳态或亚稳态.为了简化研究，做出以下假设[7-8]：

(1)空气、管外翅片与管内水三部分的热力状态在每一排中简化为集总参数，而各排管之间参数采用分排参数模型传递；

(2)换热管壁面沿四周均匀吸热或放热；

(3)不考虑管壁和水的轴向导热；

(4)忽略换热器的辐射换热；

(5)因圆柱型直通换热器空气流向与换热管垂直，空气流路与传统平面翅片管换热器类似，所以将圆柱型直通换热器等效成相同换热有效长度的平直换热管弯折而成.

传统平面翅片管换热器的建模计算一般有3种迭代模型[9-11]：集总参数模型，分布参数模型以及分排参数模型.结合圆柱型直通换热器各排结构参数不同的特点，分排参数模型最为契合换热器的结构特点，计算采用基于分排参数模型的算法.分排参数模型的思路是按照空气流向(径向)的管排数以排为单位将换热器计算划分为若干计算单元，计算单元间的参数传递遵循规律：每排出口空气物性参数为下一排空气的进风物性参数，进口水的物性参数为下一排出口水的物性参数.分排参数模型示意图如图3所示.

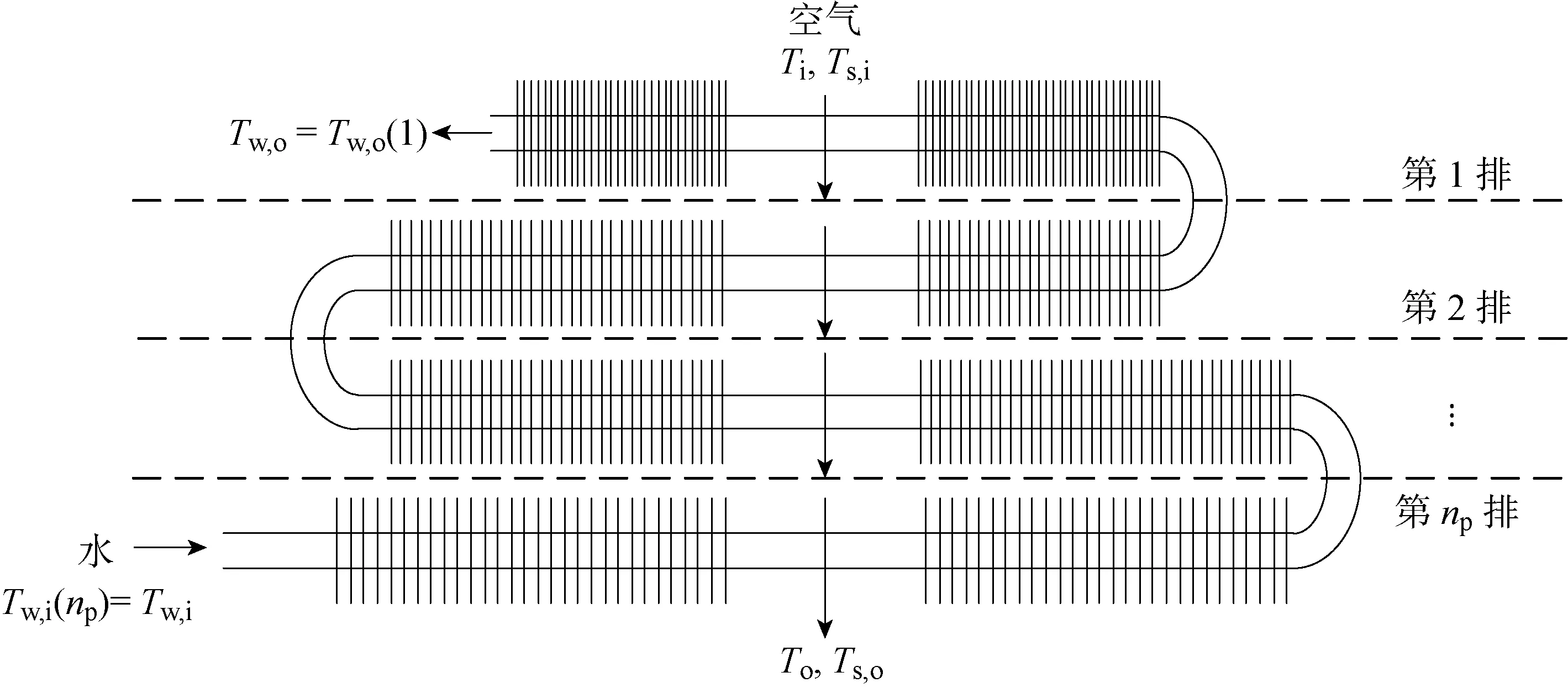
图3 分排参数模型Fig.3 Sub-row-parameter model

空气侧参数传递：

Ti(1)=Ti
Ti(2)=To(1)
Ti(3)=To(2)
…
Ti(np)=To(np-1)
Ts,i(1)=Ts,i
Ts,i(2)=Ts,o(1)
Ts,i(3)=Ts,o(2)
…
Ts,i(np)=Ts,o(np-1)

水侧参数传递：

Tw,o(np)=Tw,o
Tw,o(np-1)=Tw,i(np)
…
Tw,o(1)=Tw,i(2)
Tw,i=Tw,i(1)

其中：Ti(i)、To(i)分别为第i排换热管的进风、出风干球温度；Ts,i(i)、Ts,o(i)分别为第i排换热管的进风、出风湿球温度；Tw,i(i)、Tw,o(i)分别为第i排换热管的进水、出水温度.

在分排参数模型基础上，由于各排管的结构参数、温度不同，因此每排的换热性能参数独立计算.

析湿系数

(1)

式中：hi(i)、ho(i)分别为第i排换热管空气的进口、出口焓值；Cpm(i)为第i排管空气平均比热.

空气侧换热系数[12]

式中：λ为空气导热系数；deq为当量直径；L为径向方向的翅片长度；Re为雷诺数.

翅片表面效率

(3)

式中：ff(i)、ft(i)分别为单位管长翅片表面积、换热器外表面积；hf为当量翅高；λf为铝翅片导热系数.

圆柱型直通换热器因其换热管是一段圆弧，所以其结构参数需要根据圆和圆弧的几何特征进行计算.

(1)直径

结构设计一般已知第一排(靠近进风)换热管圆弧对应的直径，之后各排的圆弧对应直径根据径向管间距s2递推得到：

d(i)=d(1)+2(i-1)s2

(4)

式中：d(i)为第i排管圆弧对应直径；d(1)为最内圈换热管圆弧对应直径.

(2)换热有效长度

换热器的换热有效长度为换热管对应圆弧的弧长.由于需要预留空间安装冷水集流管，所以换热管并不是完整的圆周，而是圆周上的一段圆弧，圆弧尺寸由换热管对应的圆心角决定：

(5)

式中：Le(i)为第i排管的换热有效长度.

(3)翅片间距

翅片在过圆心且与换热管正交的平面上，故每排换热管的翅片间距不相等；第一排管的翅片间距最小，随着圆弧直径增大翅片间距也增大.翅片间距相当于不同直径的同心圆弧弧长，与直径成正比：

(6)

式中：sf(i)、sf(j)分别为第i,j排管的翅片间距，1≤i,j≤np.

在设计中，已知参数为中心片距(最小翅片间距)，即直径最小圆弧处的翅片间距，需要据此求出第一排管的翅片间距，再由上述关系式(6)递推求之后管排的翅片间距.中心片距sf对应圆弧直径可由翅片宽度求得，为d(1)-sf，故有

(7)

2 算法求解

制冷工况下的翅片管换热器的设计计算有3种模式[7]：已知循环风量和出水温度；已知出风干、湿球温度；已知出风相对湿度和出水温度.本文针对最常用、符合一般设计者习惯的“已知循环风量和出水温度”设计模式，建立圆柱型直通换热器的设计计算算法.换热器设计已知进风工况、水侧温度、目标制冷量Q以及基本结构参数，通过计算获取所需管排数、所需水流量以及出风状态参数.

圆柱型直通换热器的基本结构参数见表1，设计计算中基本结构参数除了径向管排数np，其它参数均为已知参数，换热器设计目的是计算确定所需的管排数.

设计计算模型为一重迭代、一层循环的算法：迭代采用绝对收敛且收敛速度较快的二分法，对各排换热管的进水温度Tw,i(i)进行求解，迭代收敛准则是管内水侧能量守恒方程(式8)计算的冷量与管外空气侧传热方程(式9)计算的能量相平衡.而计算循环是从第一排管开始，每一排迭代计算完成后开始下一排的迭代，循环终止判断为各排累加的制冷量大于等于设定制冷量.计算迭代流程图如图4所示.

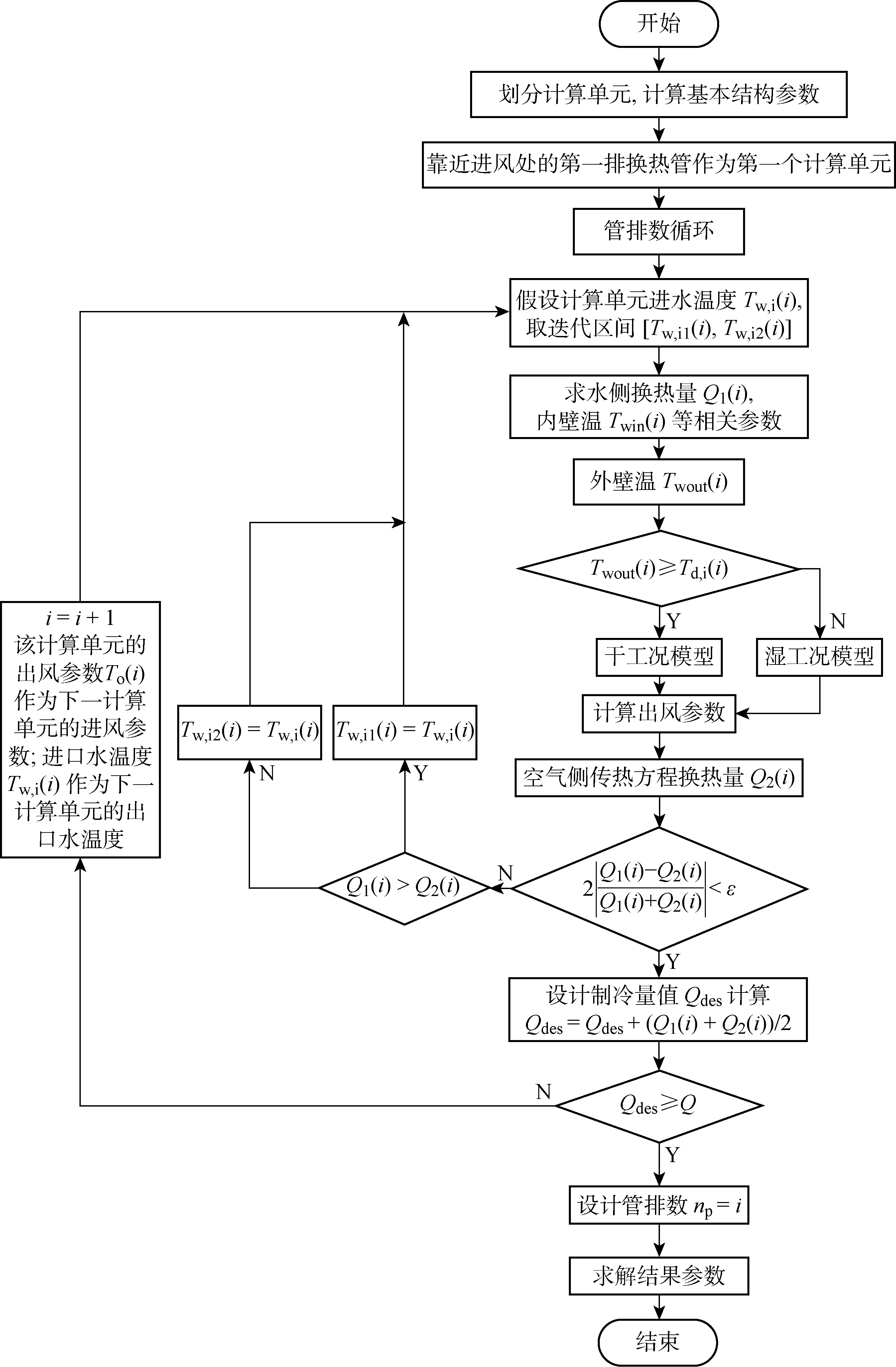
图4 设计计算流程图Fig.4 Flow chart of design calculation

Q(i)=WCpwm(i)[Tw,o(i)-Tw,i(i)]

(8)

Qa2(i)=ξ(i)ηs(i)αo(i)Fo(i)×

(9)

式中：W为水的质量流量；Cpwm(i)为第i排换热管水的平均比热容；Fo(i)为第i排的管外表面换热面积；Twout(i)为第i排管的外壁温度.

此设计模式下，设计计算完成后还需进行校核计算.校核计算本质上是根据上述设计计算确定的结构结果(即管排数)，对表冷器进行性能仿真计算，以确定表冷器的实际运行状况.校核计算模型采用两重迭代、一层循环的算法，第一重迭代(外层)的求解对象为水流量，收敛判断准则为计算的进水温度与设定进水温度相等；第二重迭代(内层)的求解对象为各排管的进水温度，收敛判断准则为管内水侧能量守恒方程(式5)计算冷量与管外空气侧传热方程(式6)计算冷量平衡.而计算循环为径向管排数的循环，从排管开始计算，一直到上述设计计算确定的排数.

校核计算的结果即为最后的计算结果，计算确定了圆柱型直通表冷器的结构(求出径向管排数)以及在相应制冷工况下的制冷运行参数.

3 计算结果分析

利用上述算法模型对圆柱型直通表冷器进行设计计算，计算结果与试验数据进行比较.试验数据为各型号的平面翅片管表冷器在不同制冷工况下通过焓差法得到，实验装置如图5所示，测试仪器及精度如表2所示.各型号平面翅片管表冷器的有效长度(Le)不同(见表3)，而其它结构参数保持相同：换热器为铜管铝翅片，管外径9.52 mm，管壁厚0.35 mm；翅片形式为双曲波纹片，翅片厚度0.12 mm，翅片间距1.814 mm；沿气流管排数2，垂直气流管排数8，沿气流管间距21.99 mm，垂直气流管间距25.4 mm；水路数4.测试的制冷运行工况如表4和5所示.

其中，工况1为标准工况，工况2为高温空气工况，进风干球温度相较工况1更高；工况3为低温水工况，在工况1的基础上降低进水温度.

采用表4和5中的工况参数作为设计计算的已知工况参数，表冷器基本结构参数设置参照表3，在此基础上对圆柱型直通表冷器进行设计计算.设计计算得到的Q与各排换热有效长度之和相等的平面翅片管表冷器全冷量数据进行比较.对于圆柱型直通表冷器，各排有效长度不相等，故通过改变换热管的圆弧直径来改变有效长度，以控制两种换热器各排的有效长度之和相等，并保持其它结构参数一致，比较结果如图6所示.

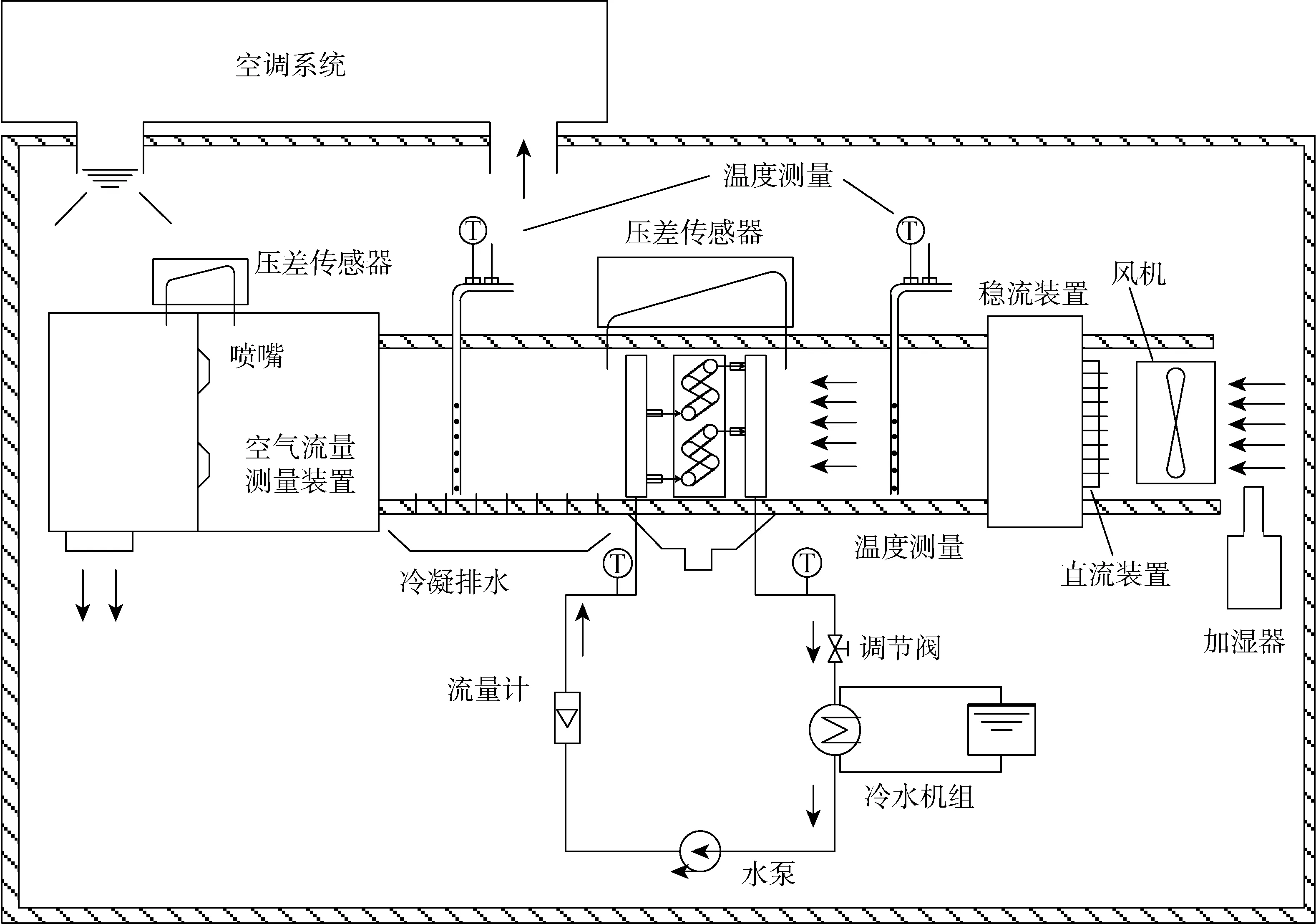
图5 实验台原理图Fig.5 Schematic of the experiment rig

表2 测试仪器及精度Tab.2 Test instrument and accuracy

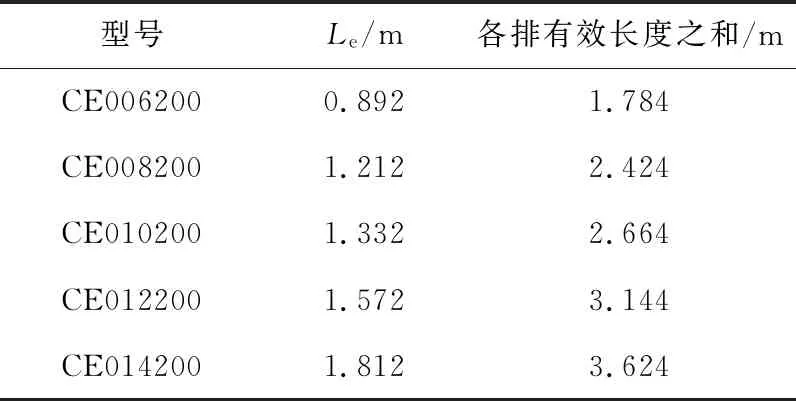
表3 各型号平面翅片管表冷器有效长度Tab.3 Structure of fin-tube heat exchanger

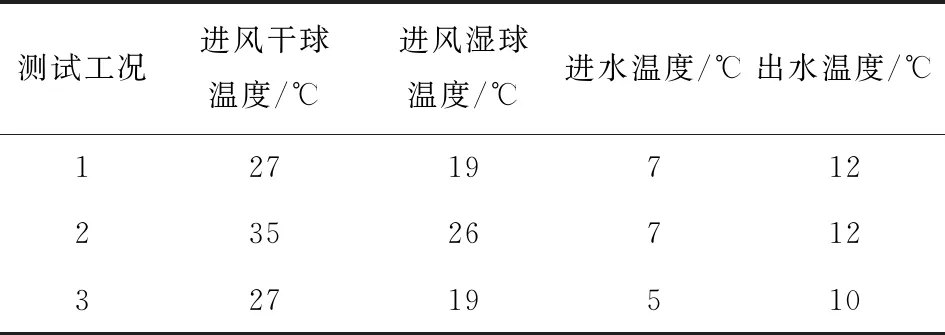
表4 制冷运行工况Tab.4 Operating conditions

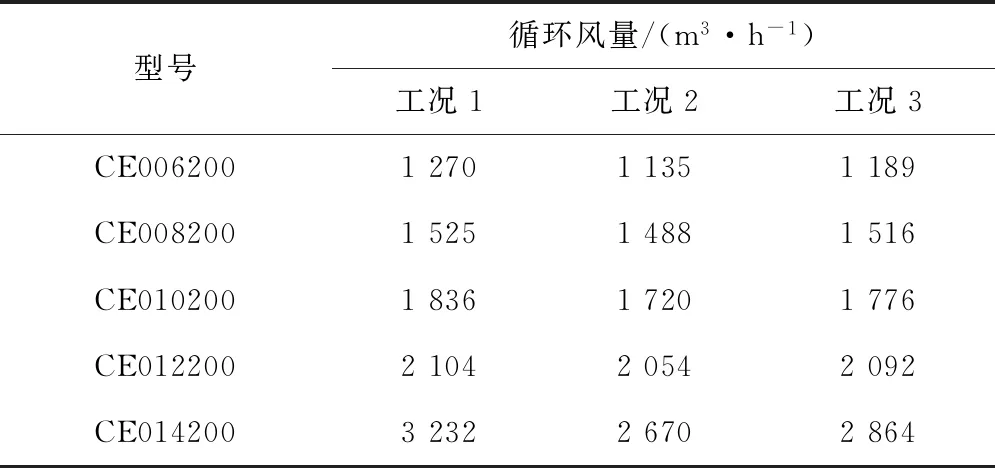
表5 制冷测试运行工况Tab.5 Operating conditions

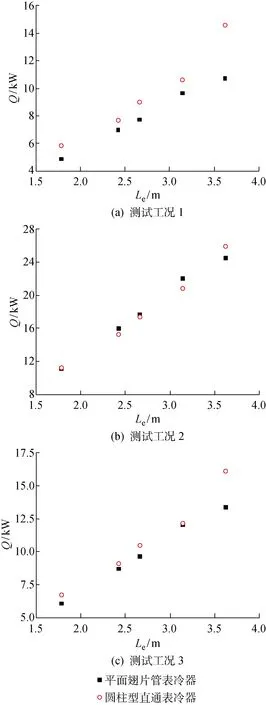
图6 模型计算结果与实验数据比较Fig.6 Comparison of model results with experimental data

从平面翅片管表冷器的实验数据与圆柱型直通表冷器的设计计算值对比结果看，随着换热有效长度的增大，两种表冷器的换热面积相应增大，冷量随有效长度的增大呈上升趋势.两种表冷器的各排换热有效长度之和保持相等，比较两者冷量可得：① 对于工况1和工况3，相同换热面积下，圆柱形直通表冷器提供的冷量比平面翅片管表冷器更大.在测试工况1下，圆柱型直通表冷器的冷量高了10%～36%，测试工况3下的增幅为1%～21%；两种工况下冷量变化趋势相似，说明降低进水温度对换热影响作用不明显；② 对于进风温度较高的工况2，平面翅片管表冷器与圆柱型直通表冷器的冷量接近，当各排有效长度之和从 1.784 m增至 3.144 m，平面翅片管表冷器的冷量较高；而取 3.624 m时结果则相反.这体现了两种表冷器的结构特点，在各排有效长度之和相等的情况下，平面翅片管换热器第一排的有效长度更大，即换热面积更大；而测试工况2的进风温度较高，因此第一排换热温差较大，其冷量也成为总冷量的主体，故平面翅片管换热器的冷量更大；③ 当有效长度取最大值 3.624 m时，圆柱型直通表冷器的冷量相比平面翅片管表冷器更大，各工况下增幅为6%～36%.

图7为两种表冷器在3种工况下的水流量W比较.比较图6和7，水流量的变化趋势与冷量的变化趋势一致：测试工况1和3下，平面翅片管表冷器的水流量小于圆柱型直通表冷器的水流量；在工况2下，只有在最大有效长度情况下，圆柱型直通表冷器的水流量才比平面翅片管表冷器高.运行工况的进出水温度已确定，根据水侧能量守恒公式(式8)，冷量与水流量呈正相关的关系，水流量的变化趋势证明了计算模型符合实际换热情况.

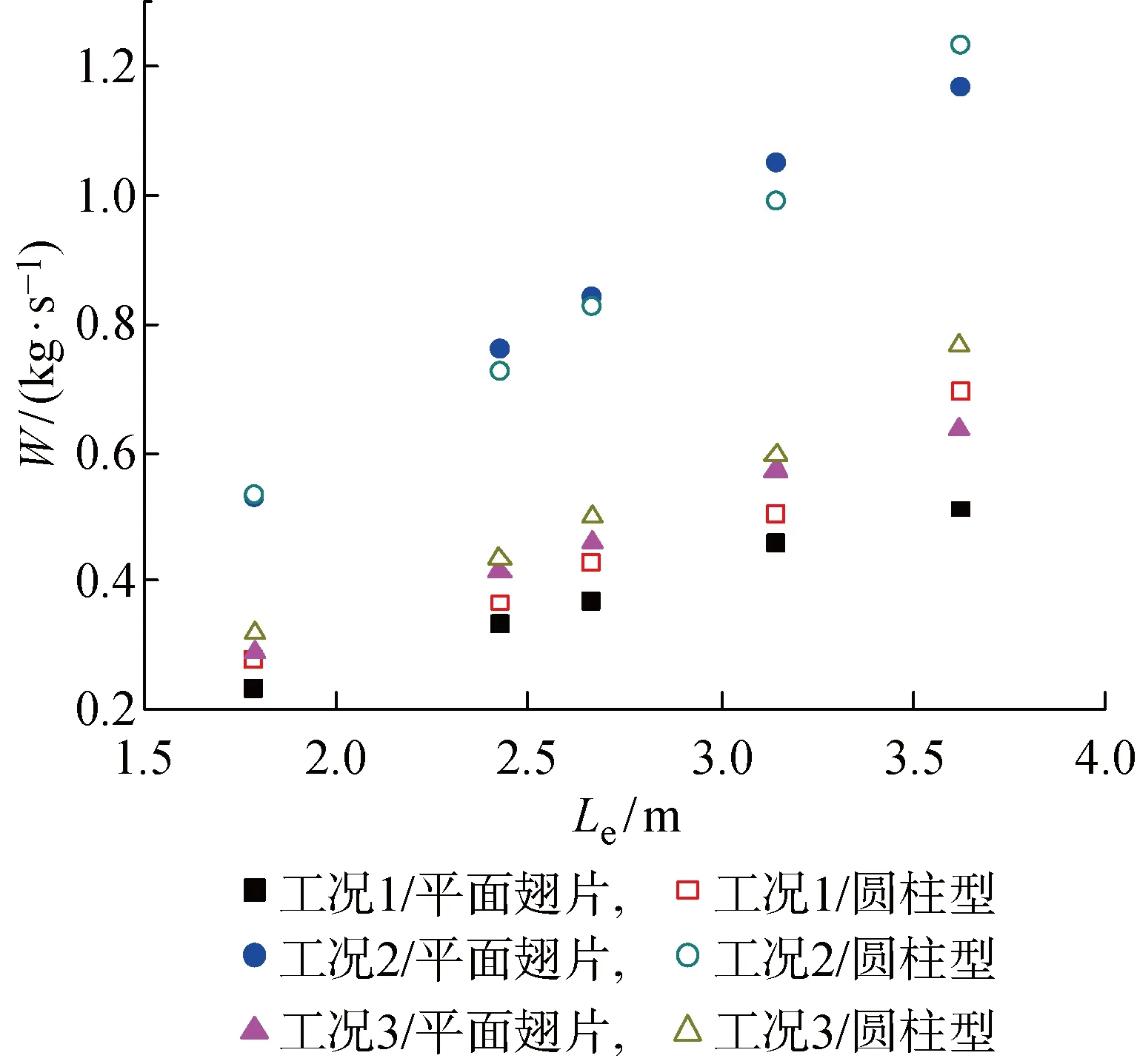
图7 水流量随有效长度的变化Fig.7 The variation of water flow rate with effective length

综上，在已知循环风量和出水温度的设计模式下，保持总换热有效长度相等，工况1与3均为圆柱型直通表冷器的冷量更大.同时因水侧的进出水温差一定，故需要更大的水流量以满足冷量的提升.降低进水温度对表冷器的换热影响作用不明显，而当进风温度升高时，两种表冷器的冷量相差不大，在小尺寸时平面翅片管换热器换热量更大，在大尺寸时结果相反.对于大尺寸表冷器(有效长度取最大值)，运行风量也会增大；当风量较大时，圆柱型直通换热器的计算冷量大于平面翅片换热管，圆柱型直通换热器的结构特点使其在大风量情况下有更好的换热性能.

由于算法基于分排参数模型，故计算可以得到各排换热管单独承担的冷量.图8为各测试工况下圆柱型直通表冷器每排换热管的全冷量.

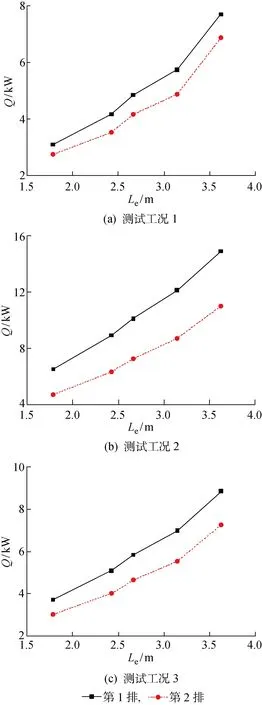
图8 表冷器各排管的全冷量Fig.8 Total cooling capacity of each row of tubes

从图8的曲线可以看出，圆柱型直通换热器各排管的冷量均随有效长度的增大呈上升趋势，这反映了换热面积随有效长度增大而增大的结构特点.由图可知，在3种测试工况下，表冷器第一排管承担的冷量均大于第二排管承担的冷量，即圆弧直径较小(内圈)的管排冷量较大.原因在于：根据表冷器的结构特点，尽管第二排换热管相较第一排尺寸更大，但其翅片间距较大，导致单位管长换热表面积更小；另一方面，第二排的迎风面积相较第一排更大，在风量不变的情况下迎面风速减小，造成空气侧换热系数的下降.因此，虽然第二排换热管的有效长度、总换热面积较大，但换热效率则降低了，最后表现为第一排换热管的冷量更大.对于工况1，第二排冷量相比第一排减小了11%～15%，而工况2则减小了26%～29%.工况2中表冷器两排管的冷量相差更大，这是因为当进风温度较高而水温不变的情况下，空气侧与水侧的温差增大，使得换热效果更好.

4 结论

出于圆柱型直通换热器数字化设计及计算分析的需要，本文对圆柱型直通表冷器的设计计算建模进行了研究，通过建立的算法模型对各工况下的表冷器进行设计计算，总结了表冷器结构设计、制冷运行等方面的规律：

(1)基于分排参数模型及数值迭代思路，建立了圆柱型直通表冷器的数字化设计算法模型.模型运算采用二分迭代法，能对制冷工况下的表冷器进行设计计算，确定所需表冷器的结构.

(2)比较在相同运行工况下的圆柱型直通表冷器设计计算冷量与平面翅片管表冷器试验冷量，在标准工况下圆柱型直通表冷器的冷量大于平面翅片管表冷器的冷量.在保证进出水温差一定的前提下，冷量的增大需要提高水流量以实现.减小进水温度对换热影响作用不明显，而若增大进风温度，平面翅片管表冷器的换热效果更好；故对于高温空气工况，采用平面翅片管表冷器更有优势.

(3)圆柱型直通表冷器在结构尺寸较大、运行循环风量较高时的计算冷量大于平面翅片管表冷器的冷量，圆柱型直通表冷器外圈翅片密度减小、迎风面积增大的结构特点并没有使其总冷量下降.

(4)模型计算结果反映了圆柱型直通表冷器各排换热管的冷量分布规律：靠近进风的前排换热管虽然相比后排换热管其有效长度、换热面积较小，但由于较小的翅片间距以及较高的迎面风速，其换热效率更高，冷量更大.