基于Ansys下跨度对工字形曲梁非线性稳定的影响
王晓雪,张芳芳
(山西大同大学建筑与测绘工程学院,山西大同037003)
在工业和民用建筑中,曲梁建筑以其弧线流畅,选型美观,越来越受到桥梁与建筑设计者的青睐和欢迎。钢曲梁通常用于拱一类的构件中,即曲梁腹板和外荷载的作用都在曲率平面内;而水平曲梁,其腹板与曲率平面垂直,所以在竖向荷载的作用下,初始变形既弯又扭,工作性能比较复杂,具有非均匀扭转的翘曲现象,如果根据线性平衡分析理论是不能符合其受力情况的,所以对其研究难度较大[1]。
近些年随着计算机技术的蓬勃发展,有关这方面的分析软件也起来越成熟。本文基于Ansys 软件,对水平曲梁在竖向均布荷载作用下,其结构稳定的极限荷载以及结构失稳状态下的应力、应变、失稳模态、上下翼缘和腹板的塑性发展等情况进行分析研究[2]。
1 几何模型
由于工程中工字形曲梁应用较多,制造方便,截面形状符合应力特点,所以本次实验采用双轴对称的工字形曲梁,截面尺寸为600×300×11×17 mm,圆心角为10°,跨度分别为4 m、6 m、8 m和10 m,两端均为固定支座,见图1。
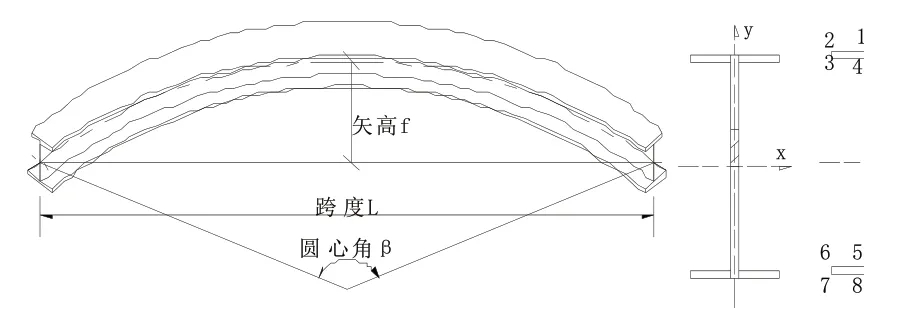
图1 钢曲梁几何模型
为了描述不同位置的变形及弹塑性状态,对截面各单元位置编号,见图2。在荷载作用下,每一单元的位移、应力、应变及塑性发展情况都不一样。

图2 曲梁断面节点和单元位置编号
2 选取单元类型
Ansys 软件常用的有限单元有Link 单元、Beam单元、Block 单元和Plane 单元等。为了更形象、真实、准确地描述钢曲梁各部分(如上翼缘、下翼缘、腹板)在荷载作用下的位移和应力情况,在此选择Block 块单元中的实体单元SLID45,采用间接法先建立实体模型。由于工字形曲梁截面尺寸恒定,形状规整,所以划分为矩形网格,见图3。

图3 钢曲梁单元模型
3 定义材料物理特性
在Ansys 有限元计算中,钢曲梁模型均采用钢材Q235,材料密度为7 850 kg/ m3,弹性模量E=206 GPa,泊松比μ=0.3,屈服强度σy=235 MPa,屈服后切线模量为6.18 GPa。
4 计算结果分析
划分网格之后,对该实体模型进行满跨施加竖向荷载,并作用在上翼缘,边界约束为固定支座。
图4~图6 分别给出了支座处、1/4 跨、半跨处在外力达到极限荷载时,各跨度曲梁横截面的扭曲变形模态图。从图可知,各曲梁在荷载作用下,支座处由于是固定约束,其位移受到限制,所以直接进入塑性变形状态。塑性首先从上翼缘靠近圆心一侧开始,继而发展到较远的一侧;而下翼缘塑性开展次序正好与上翼缘相反,塑性区也比上翼缘面积小;腹板是靠近上翼部位较大,靠近下翼缘次之,中间部分最小,这点与直线梁受力时截面正应力分布有所相似。

图4 曲梁支座处塑性发展断面图

图5 曲梁失稳时1/4跨处断面塑性区分布图

图6 曲梁失稳时1/2跨处断面塑性区分布图
图6还显示在极限荷载下,跨中截面塑性区域发展程度最小,主要集中在上翼缘,跨中腹板和下翼缘区域塑性则很小。跨中截面产生的应力也很大,所以实际应用上应力卸载对曲梁的承载能力影响不大。
比较各跨曲梁的变形模态图,跨度越小,塑性扭曲变形越小,截面的侧向位移也越小;跨度越大,上翼缘的翘屈也越厉害,腹板屈曲次之,下翼缘则最小。沿曲梁纵向各部位的弯扭侧移跨中远大于其他部位,所以曲梁的失稳破坏基本都是由于跨中扭屈变形太大而发生[3]。
图7和图8是1/4跨和1/2跨处上翼缘相同部位的荷载位移曲线图。由图可见,在荷载作用初始,两个部位处曲梁荷载位移曲线都呈正比的弹性变形阶段,跨度越小,弹性阶段的稳定荷载越大。对于同一跨度的曲梁,其1/4跨和1/2跨处的稳定临界荷载大致相同,但位移却相差较大。

图7 1/4跨处荷载位移曲线
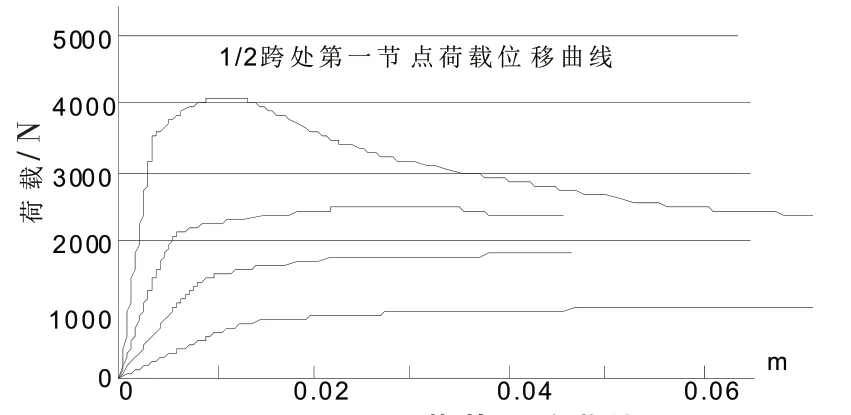
图8 1/2跨处荷载位移曲线
对于几种不同跨度的曲梁,在达到稳定临界荷载时,荷载大小相差极大。在相同的荷载作用下,跨度越大,曲梁相应的位移就越大。对于跨度小的曲梁,在荷载作用下的初期,位移曲线基本上成直线增长趋势,在临近极限荷载时,曲梁位移迅速增加,说明这时曲梁进入塑性状态(荷载应力曲线也充分说明这一点),且有明显的弹塑性阶段,而跨度大的曲梁较早就呈现出非线性增加的态势。而跨度较大的曲梁,在进入塑性状态时,荷载增加不大的情况下,位移却继续急剧增加,进而导致失稳而破坏[4]。
图9和图10是荷载应力曲线图。1/4跨和1/2跨处荷载应力曲线显示跨度较小的曲梁在稳定荷载作用下,基本呈现弹性阶段,变形很小,随着跨度增大(跨度大于8 m),曲梁的弹性阶段变短甚至没有明显的弹性状态,而且较早进程入塑性区,塑性区发展不深便由于侧扭屈曲而失稳,失去承载能力。

图9 1/4跨处荷载应力曲线

图10 1/2跨处荷载应力曲线
曲梁失稳时的塑性发展情况,见表1。由表1可看出,对于较小跨度(如4 m 跨)曲梁失稳时,梁端部全部进入塑性变形,曲梁的失稳是因为支座处梁端区域塑性变形开展太大,使其抗侧扭能力降低,从而导致构件扭屈失稳的。对于跨度较大的曲梁,在达到临界荷载时,跨中截面塑性区也主要集中在上翼缘;在圆心角比较小的时候,塑性区主要在上翼缘接近曲率中心近的一侧。随着圆心角增大,在上翼缘离曲率中心较远一侧也会出现塑性区,且是受拉屈服。而且实验有关数据也说明:较长的曲梁,随着跨度增加,承载力在初始下降很快,后来变化趋于平缓。
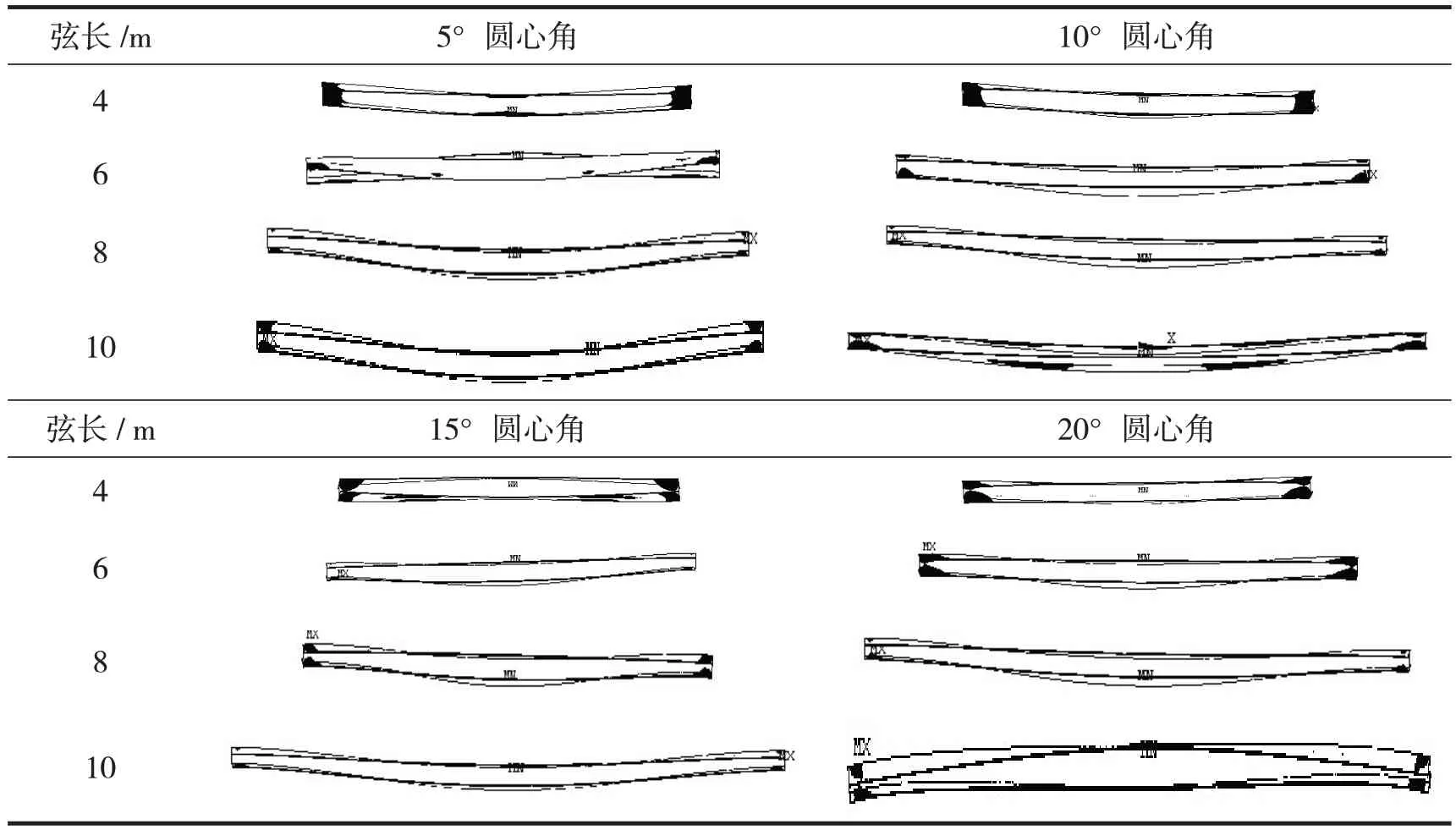
表1 曲梁失稳时的塑性发展情况
5 结论
(1)对于跨度较小的曲梁,跨中断面塑性是首先发生在上翼缘离曲率中心较近一侧,然后曲率中心较远一侧随着荷载的继续作用也进入塑性。随着外荷载的增加,下翼缘受拉部分也逐渐进入塑性,荷载再继续增加,塑性区在逐渐开展,直至腹板上端也开始进入塑性。此后,下翼缘塑性开展加快,当曲梁达到极限荷载时,下翼缘完全处于塑性阶段,而上翼缘仍有一小部分处于弹性阶段,腹板大部分也处于屈服状态。所以,曲梁基本上是先塑性开展,再侧向弯扭破坏。跨中截面塑性区主要集中在上翼缘,支座处上下翼缘的塑性都比较大。
对于跨度较大的曲梁,荷载较小时,塑性开展初始与小跨曲梁相似,但当达到极限荷载时,跨中截面塑性区也仍主要集中在上翼缘部分。
(2)曲梁的破坏形式大多是弹塑性侧扭破坏。对于跨度较小的曲梁,在未达到极限荷载以前位移基本成线性变化,随着加载增大便进入弹塑性阶段,然后呈现侧向弯扭,在临近最大荷载时侧向位移和扭转角急剧增加,整个情况类似于直梁的整体失稳[5]。
而对于跨度较大的曲梁,构件的抗扭刚度低,曲梁的侧扭破坏和弹塑性屈服同时进行,若跨度再大时(大于8 m),则刚进入弹塑性阶段,却已弯扭变形过大而不能继续承载。这也说即便对于相同曲率的曲梁,破坏模式也不相同。跨度较小的梁达到极限承载力时的屈服区域,要明显高于跨度较大的梁。
(3)工字形截面水平钢曲梁随着圆心角和跨度的增加,构件的抗扭刚度降低,曲梁的失稳是由于塑性区域的发展和弯扭变形共同作用引起的;同时随着圆心角和跨度逐渐增大,曲梁失稳时的弯扭变形也越来越大,且最大应力出现在梁端,最大位移出现在跨中;若跨度再继续增大时,还未达到极限荷载曲梁就已弯扭失稳破坏。
(4)工字形截面水平钢曲梁在竖向均布荷载作用下,其变形弯而扭。随着荷载作用增大,竖向弯曲加大,侧向位移和各部位截面扭转角位移也都在增加。外力产生的二阶效应也随之增加,这些都会使曲梁较早地进入弹塑性阶段。
(5)在竖直荷载作用下,工字形曲梁在弯曲的同时会出现扭屈。这样在曲梁截面上除了挠曲应力外,还有扭转带来的剪应力和翘曲正应力,当曲梁进入弹塑性阶段后,截面上弯曲应力和扭转应力之间就不能保持已有的比例关系[6]。
6 结语
根据Ansys模拟曲梁承载的最大能力以及失稳破坏情况,不仅可以根据截面选取最经济的各跨曲梁,还可以据曲梁各部位弯扭破坏的深度和形态,改变截面形式或钢板厚度,以满足荷载和结构稳定的要求,以达到物尽其材,发挥最大的经济作用。

