善建数学模型，解决实际问题

☉江苏省宜兴市楝树中学 缪小龙

数学建模就是通过对实际问题的抽象与提升，即只提取其中的数量关系、位置关系与图形形状，然后，用数学语言对实际问题进行近似的刻画，使我们对研究对象有更深刻的认识.要进行数学建模，不仅要掌握必要的知识类模型，如概念、运算法则、定理等，而且要掌握必要的应用类模型，如方程与方程组、不等式与不等式组、各类函数、特殊三角形、特殊四边形、统计中的“三数”与“三差”、概率等.本文以问题为例主要讲述应用类模型在实际问题中的建立与转化.

一、建立方程模型解决实际问题

方程模型是研究现实世界等量关系的数量模型，如现实生活中的行程问题、工程问题、销售问题、利率问题、面积和体积问题等，当我们只关注其中的等量关系时，就建立了方程模型，通过方程或方程组的解答，达到对实际问题的解决.

例1组织“大手拉小手，义卖献爱心”活动，购买了黑和白两种颜色的文化衫共140 件，进行手绘设计后出售，所获利润全部捐给山区困难孩子.每件文化衫的批发价和零售价如表1 所示：

表1

假设文化衫全部售出，共获利1860元，求黑、白两种文化衫各多少件.

分析：设黑色文化衫x件，白色文化衫y件，依据“黑文化衫的件数+白文化衫的件数=140”建立第一个方程，依据“售黑文化衫的利润+售白文化衫的利润=1860”建立第二个方程，然后解方程组求解.

解：设黑色文化衫x件，白色文化衫y件，依题意得

点评：建立方程或方程组的数学模型解决实际问题，当直接设未知数不易建立方程时，就间接设未知数，当设一个未知数建立方程不易理解时，可以再设一个辅助未知数.一般设几个未知数就列几个方程，从不同的角度建立不同的方程.

二、建立函数模型解决实际问题

现实世界是广泛联系与永恒运动的，在数量关系中有运动变化问题，在空间形式中也有运动变化问题，而函数就是研究两个变量之间变化规律的数学模型，实际生活中的最大利润、最低成本、最优方案等问题，都可以通过建立函数的数学模型，然后运用函数的性质对问题进行分析和解答.

例2苏果超市销售一种饮料，每箱进价是24元，按照超市相关规定，销售的价格不能低于进货价.现在售价统一规定为一箱36元，每月能销售60箱.通过市场调研发现：如果这种饮料的销售价格每降低1 元，那么，每个月的销售数量将增加10箱，如果每箱饮料降价x元（x是正整数），每个月的销售数量为y箱.

（1）请写出y和x间的函数关系式与自变量x的取值范围；

（2）超市应怎样定价，才能使每个月销售饮料的利润达到最大？最大利润是多少元？

分析：（1）根据价格每降低1元，平均每月多销售10箱，每箱降价x元，多卖10x箱，因为是在36元的基础上降价，在60箱的基础上多卖，所以降价后的价格为（36-x）元，卖出的箱数为60+10x；（2）根据“总利润=每箱利润×箱数”列出函数关系式，然后根据二次函数最值的性质求得最大利润.

解：（1）根据题意，得y=60+10x.由36-x≥24，得x≤12.由x为正整数，得x≥1，则1≤x≤12，且x为整数.

（2）设所获利润为W，则W=（36-x-24）（10x+60）=-10x2+60x+720=-10（x-3）2+810.

则当x=3时，W取得最大值，最大值为810.

点评：当实际问题中有两个变量，且它们之间有一定变化规律时，就建立函数关系式，根据实际问题求出自变量的取值范围.求最值问题一般要利用二次函数最值的性质，若建立一次函数关系求最值，则要利用自变量的取值范围与一次函数的增减性.

三、建立独特几何图形模型解决实际问题

实际生活中的测量、航海、建筑及图案设计等都离不开几何模型，而数学中的空间与图形研究的就是几何图形的大小、位置关系、性质及变换，在实际问题中，只要我们把实际问题进行抽象与概括，画出符合题意的几何模型，然后利用几何图形的性质、判定及相互变换关系就可以解决实际问题.

例3如图1所示，一铁路MN和一公路PQ相交于点O处，∠QON=30°，一幢居民楼位于点A处，AO=320m，假设一火车行驶时，在其周围相距200m内会受噪音的干扰，则火车于铁路MN上沿着ON这一方向行驶的时候，

（1）居民楼是否会受到噪音的影响？请说明理由；

（2）假设行驶速度为72km/h，则居民楼被噪音干扰的时间为多久？

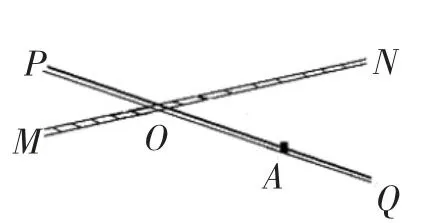
图1

图2

分析：（1）居民楼是否受噪音的影响，主要看火车距离居民楼最近时是否受影响，如果距离最近时受到影响，那么就受到影响，如果距离最近时不受影响，那么就不会受到影响.所以应作AC⊥ON于点C，然后比较AC的长与200m的大小关系，从而可判断是否受到影响.

（2）火车行驶时，周围200m以内会受到噪音的影响，也就是说当火车距离居民楼200米时，居民楼就会受到影响，因为最近距离160米＜200米，所以在点C之前和之后会各有一个点距离点A200米，当火车在线段BD上行驶时，居民楼都会受到影响.最后利用时间=路程÷速度求得受影响的时间.

解：（1）如图2，过点A作AC⊥ON于点C.

由∠QON=30°，OA=320米，得AC=160米.

由AC＜200，得居民楼会受到噪音的影响.

（2）如图2，在ON上取两点B、D，使BC=CD，设BA=DA=200m，即当火车到点B时直到驶离点D，对居民楼产生噪音影响.

因行星轮系具有运行噪音小的特点，能够给乘坐者提供舒适感与安全感，其较长的使用寿命也为电梯的长时间运行提供保证，此外，行星齿轮曳引机的效率远高于同样提升力的蜗轮副式曳引机，且体积仅是它的一半[2]，因此，在曳引机设计中，行星齿轮减速器较其它形式的齿轮传动系统更具优势。某型号电梯的曳引机减速器使用2级行星轮系 [3]，该项目选取串联的2个2K-H型行星轮系进行设计。

由AB=200米，AC=160米，根据勾股定理，得BC=120米.由垂径定理，得BD=2BC=240米.

72千米/小时=20米/秒，240÷20=12（秒）.

答：影响时间是12秒.

点评：本题根据题意建立了含30度角的直角三角形和等腰三角形两种几何图形模型，然后利用含30度角的直角三角形的性质：30度的角所对的直角边等于斜边的一半解决了居民楼是否受影响的问题；利用等腰三角形三线合一的性质求得了受影响时火车行驶的路程，最后利用时间=路程÷速度的模型求得受影响的时间.这是一个利用几何图形模型解决实际问题的典型实例，其关键是构造符合题意的几何图形.

四、间接建立数学模型解决疑难问题

有些问题直接建模如果有困难，可以间接建模求解，如有些代数问题需建立几何图形的模型解决，有些几何问题需建立代数的模型解决，这种方法称为建模转型.这种方式不常用，常出现在竞赛试题中，它往往能使疑难的问题变得简单、易懂.

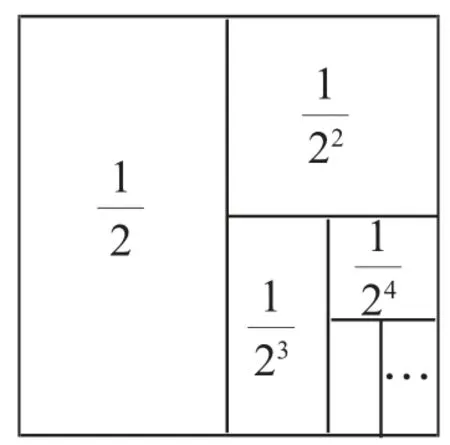
图3

解：因为每次截取原来的一半，所以n次截取后，木杆剩下的长度为这个问题相当于：面积为1的正方形第一次剪去，第二次剪去剩下的，第三次又剪去剩下的，当n次剪取后剩下的面积是多少？如图3所示，我们发现第一次剩下，第二次剩下，第三次剩下，第四次剩下，……，所以第n次截取后剩下米.

点评：本题首先将实际问题转化为有理数的计算，然后把有理数的计算转化为图形面积问题，再通过对图形的观察直观地得到结果，这种不断取的几何模型，也可用来计算的结果.

数学源于生活，但又高于生活，反过来又服务于生活，教学的改革越来越重视数学知识与现实生产、生活的联系，通过数学教学，培养学生的数学应用意识与能力，是数学教学的重要任务之一.通过以上事例的解析与说明，我们已经可以看出数学建模无处不在，应用它可解决生活中的诸多问题，这不仅需要掌握一些必要的知识性模型，而且要善于从数学的角度看待生活中的人和事，发现其中的数量关系、位置关系或变换关系.W