昆虫目标雷达散射截面积特征辅助跟踪算法
方琳琳 周 超* 王 锐 胡 程
①(北京理工大学信息与电子学院雷达技术研究所 北京 100081)
②(卫星导航电子信息技术教育部重点实验室(北京理工大学)北京 100081)
1 引言
昆虫雷达可以实现对迁飞性害虫的迁飞轨迹进行监测和预警,是预防虫害虫灾异地爆发的有效工具[1]。昆虫目标的体积小,飞行高度低,并且回波幅度微弱,当信噪比(Signal Noise Ratio,SNR)较低时,为保证高检测率,通常设置较低的检测门限,但由此会带来大量的虚警点,进而导致在目标跟踪的数据关联环节,受虚假量测的影响,数据关联的准确度下降。基于幅度特征辅助的跟踪算法是一种提高数据关联准确度的有效方法[2],其利用源自目标与噪声点迹的幅度差异来提高目标与噪声的识别度,改善跟踪性能,但是其需要目标的雷达截面积(Radar Cross Section,RCS)起伏模型作为先验信息来计算幅度似然比。因此,对于不同种类目标在不同杂波背景下的跟踪,该方法的关键在于如何得到目标和杂波点迹的幅度分布信息以及相应的幅度似然比。
Bar-Shalom等人[2]在1990年提出利用雷达回波中的幅度信息来辅助跟踪目标,研究了幅度信息在数据关联环节中的应用,推导了瑞利分布目标在高斯白噪声背景下的幅度似然比,来修正点迹与航迹的数据关联概率值,并进一步将其应用到交互多模型(Interacting Multiple Model,IMM)算法中[3],通过不同的仿真场景验证了该方法的有效性。为适应更多复杂场景,2010年,Brekke 等人[4]将该方法应用到非瑞利分布杂波背景下的弱目标跟踪,推导了K分布杂波背景下的幅度似然比,并分析了相应的跟踪性能。文献[5]中推导了Swerling 1型目标在Weibull,Log-normal等杂波背景下的幅度似然比。为适应更多目标模型,文献[6]中推导了Swerling 3型目标在高斯白噪声背景下的幅度似然比,并通过仿真实验评估了跟踪性能。
现有幅度辅助跟踪算法的应用场景均是针对Swerling型目标在高斯白噪声及不同杂波背景下的跟踪。对于昆虫目标,需首先建立相应的RCS起伏模型,为幅度似然比的推导提供先验信息,进而得出适用于昆虫目标的幅度辅助跟踪算法。但是昆虫目标的RCS较小,同时受极化方式、电磁频率、观测角度和自身的翅膀拍动等多种因素影响,通常表现出随机不规律的起伏,需基于统计理论分析其RCS特性,并建立相应的起伏模型[7]。
因此,本文首先基于Ku波段昆虫雷达夜间观测到的昆虫目标实验数据,根据雷达方程等理论分析得出目标RCS随时间起伏变化的采样值,然后采用最小二乘拟合及Kolmogorov-Smirnov(K-S)拟合优度检验方法,得出Gamma分布可以较好地拟合昆虫目标的RCS概率分布。在此基础上,推导出Gamma起伏型目标在高斯白噪声背景下的幅度似然比,并将其融合到概率数据互联滤波器中,通过在不同SNR、不同量测噪声下的仿真分析得出,RCS特征辅助的跟踪算法可以有效地提高目标跟踪精度。
2 昆虫目标RCS起伏模型建模
RCS特征辅助跟踪算法需已知昆虫目标RCS起伏模型作为先验信息,由于昆虫目标的RCS受多种因素影响,并且是时变的,起伏表现出随机不规律的特性,在工程实践中很难快速、实时地获得目标在任意实验环境下的RCS真值。为了更加准确地描述目标动态RCS的起伏特性,通常将其当作随机变量,利用统计理论对其进行建模分析[7]。图1所示为建模过程。
2.1 昆虫目标RCS数据获取
本文基于Ku波段高分辨昆虫雷达采集的夜间高空自由飞行昆虫的动态RCS数据,对昆虫目标RCS起伏的统计特性进行了建模分析。雷达的中心频率为16.2 GHz,带宽为800 MHz。实验场景如图2所示,雷达放置在高空诱虫灯旁边,垂直对天观测。选择飞行高度为200~400 m范围内采集到的昆虫回波数据。由于雷达垂直对空观测,观测场景干扰很少,完成目标检测之后,基于目标的运动特性和时频分析辨别出昆虫目标,并提取出回波信号。

图1 昆虫目标RCS起伏建模流程图Fig.1 The flow chart of insect RCS fluctuation modeling

图2 实验场景Fig.2 The experimental scene
由雷达方程可知,回波信号的瞬时功率与目标的RCS成正比[8],并且与目标在雷达波束中的位置有关,受主瓣内天线方向图调制[9]的影响。因此,在消除波束主瓣增益的影响后,得到随时间变化的RCS起伏值(∆σ),进而分析RCS起伏的统计分布特性。
2.2 分布特性拟合及拟合优度检验
本文首先采用最小二乘拟合方法将实测昆虫目标RCS起伏分布与χ2,Gamma,Log-normal,Weibull分布模型[10]进行拟合分析,拟合误差表达式为
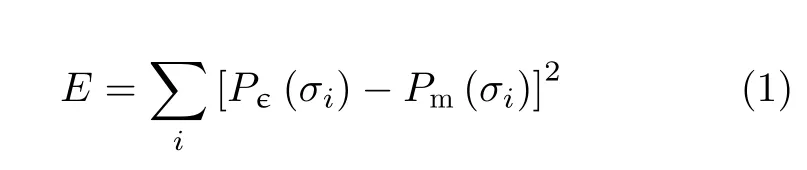
其中,Pϵ(σi)为RCS数据在不同区间的概率值,Pm(σi)为统计模型拟合得到的相同区间的概率值。图3所示为RCS起伏概率密度函数(Probability Density Function,PDF)拟合结果,实验中随机挑选的10只实测昆虫RCS起伏拟合误差如图4所示,每只昆虫目标的RCS采样点数在1300~1500之间。可以看出,χ2分布与实测数据差异较大,Log-normal分布和Gamma分布拟合结果最接近实际昆虫RCS起伏PDF,但Gamma分布拟合结果略优于Log-normal分布的拟合结果。
为进一步衡量曲线的拟合效果,本文采用KS拟合优度检验方法[10]对上述实验数据的拟合结果进行了验证,K-S检验公式为

其中F′(x)表示样本数据的累积概率函数,即目标RCS起伏值的统计累积概率分布,F(x)为分布模型的拟合累积概率函数,D值表示K-S检验参数。对应的累积分布函数(Cumulative Distribution Function,CDF)拟合结果及K-S拟合优度检验参数如图5和图6所示。可以看出,Gamma分布的D值最小,这说明昆虫RCS起伏分布最接近Gamma分布,与PDF的分析结果一致。
从曲线吻合程度、拟合误差和拟合优度检验结果可以看出,相比于其他3种模型,Gamma分布可以较好地拟合昆虫目标RCS起伏的统计特性,为昆虫目标RCS辅助跟踪算法幅度似然比的计算奠定了理论基础。
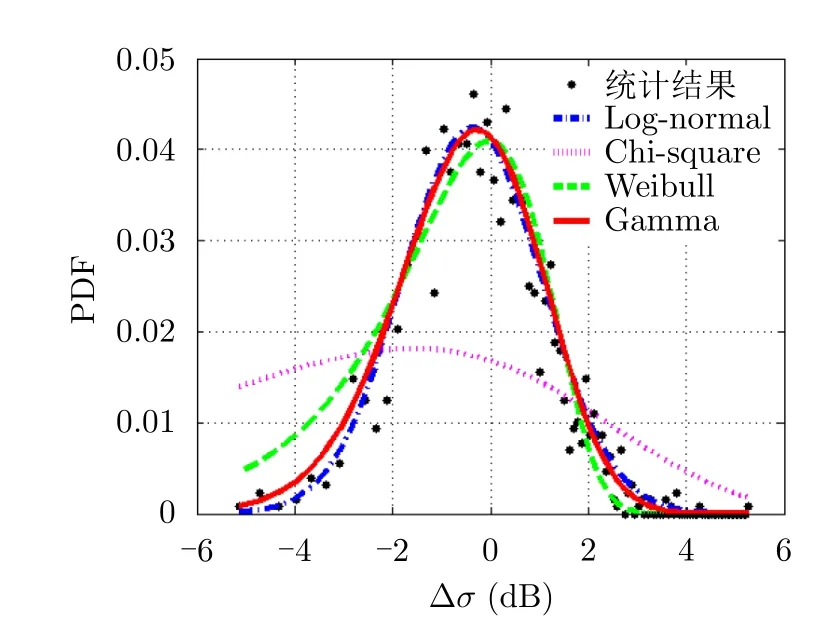
图3 PDF拟合结果Fig.3 PDF fitting results
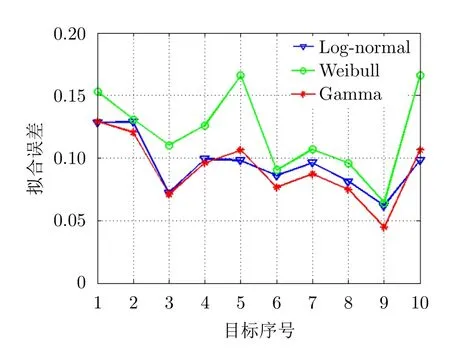
图4 拟合误差Fig.4 Fitting error

图5 CDF拟合结果Fig.5 CDF fitting results

图6 S检验参数Fig.6 K-S test parameters
3 昆虫目标RCS特征辅助跟踪算法
基于昆虫目标RCS起伏模型,本文推导了Gamma起伏目标在高斯白噪声背景下的幅度似然比,将其作为加权因子修正了概率数据互联算法中的点迹与航迹的关联概率值,有效地提高了数据关联环节目标与噪声的识别度,改善了航迹精度。算法实现流程如图7所示。
传统的概率数据互联滤波(Probabilistic Data Association Filter,PDAF)算法[11]通过计算相关波门内的确认量测来自目标的概率,对相关波门内的不同回波进行加权,利用各个候选回波的加权和来对目标的状态进行更新。
目标状态更新方程为

图7 目标RCS辅助跟踪算法实现框图Fig.7 RCS aided tracking algorithm implementation block diagram
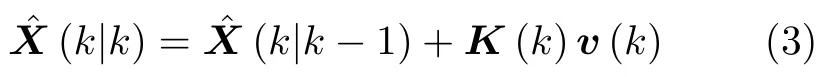
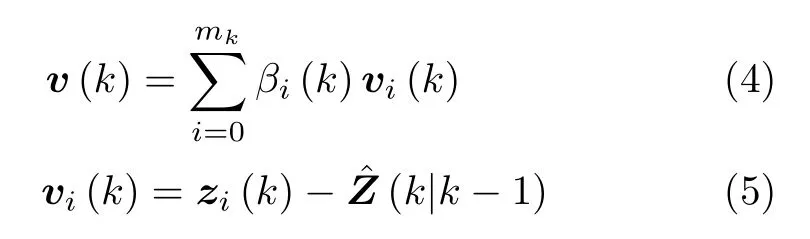
其中,mk表示k时刻相关波门内的量测总数,vi(k)为与该量测值相对应的新息,zi(k)为量测值,(k|k-1)为量测预测值,βi(i=1,2,···,mk)为第i个候选量测源于目标的条件概率,β0为候选量测中没有一个量测源于目标的概率。具有泊松杂波模型的概率[11]为

定义

则


其中,PD为目标检测概率,PG为门概率,Vk为相关波门的体积,λ为虚假测量的空间密度,λVk为相关波门内的虚假量测数,S(k)为k时刻的新息协方差,γ为波门大小,nz为量测维数。
3.1 幅度辅助概率数据互联算法
幅度辅助概率数据互联算法(Probabilistic Data Association Filter with Amplitude Information,PDAF-AI)利用幅度似然比ρ来修正数据关联环节中点迹数据与航迹的关联概率β,使得经过综合加权后的状态更新值更加准确,幅度似然比[2]表示为

其中,a表示幅度信息,τ为检测门限,PD为目标的检测概率,PFA为虚警概率,pT(a)和pF(a)分别表示在未经过门限检测时,目标和噪声的幅度概率密度函数。
加权后的关联概率[2]β表示为

3.2 昆虫目标幅度似然比计算
基于昆虫目标的RCS起伏模型,本小节推导了在高斯白噪声背景下Gamma起伏目标的幅度似然比计算公式。
目标检测可以表示为二元假设检验问题

其中,n是均值为零,方差为的高斯白噪声,s表示幅度为A,相位为θ的目标信号,表达式为s=Aexp(jθ),相位θ为在(0,2π]内均匀分布的随机变量。
在H0假设下,目标不存在,|z|的PDF为瑞利分布[12],表示为

在H1假设下,对于非起伏目标,目标信号幅度A为恒定值,|z|的PDF为莱斯分布[12],表示为
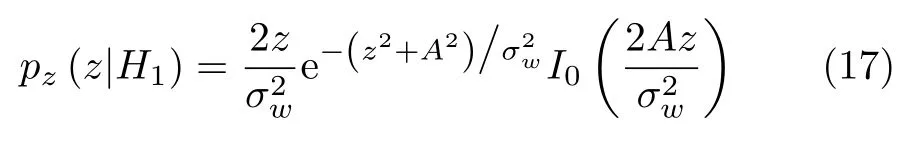
对于起伏目标,目标幅度A的 概率分布为pA(A),此时

设目标RCS值表示为X,那么目标幅度,对X的概率密度函数进行下面的变换可以得到幅度A的概率密度函数
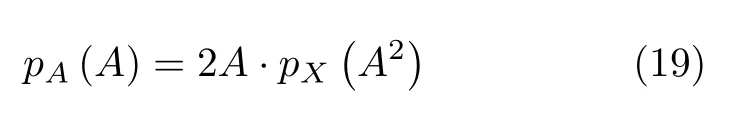
如果目标RCS值X服从尺度参数为Ω,形状参数为v的Gamma分布,其PDF表示为

则根据式(19)和式(20)得出,目标幅度A的概率密度函数为
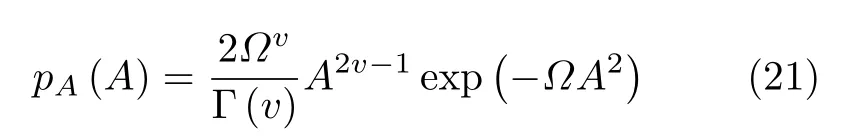
将pA(A)的表达式带入式(18)中,得

根据第1类修正贝塞尔函数Ia(x)与第1类贝塞尔函数Ja(x)的关系[13]

并利用积分关系式[13]
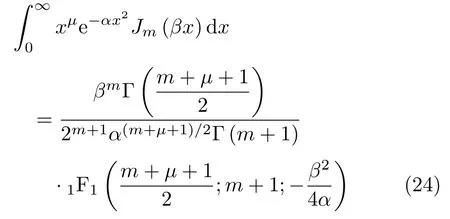
得出
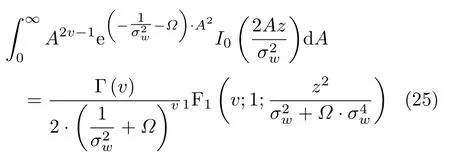
即

其中,1F1(•;•;•)为合流超几何函数。
因此,幅度似然比表达式为

当跟踪波门内有多个量测点时,需将每个量测点的幅度值|zi|带入到式(27)中,得出对应于每个量测点的幅度似然比ρi,将其带入到式(13),(14)中即可得出每个量测点的修正关联概率值。
4 仿真实验
4.1 性能评价指标
为了更好地评估算法性能,本文采用以下性能评价指标对跟踪结果进行性能分析。
(1)均方根误差(RMSE)

其中,N为蒙特卡洛仿真次数,(X,Y)为直角坐标系下目标的无噪声真实测量值,为滤波值,j表示帧号。
(2)有效航迹条数
如果在k时刻的位置误差超过了第1门限T1,且不能在m帧能够回到T1之下,则认为此条航迹在k时刻无效;如果能够在m帧之内回到T1之下,则认为该航迹有效;如果位置误差在k时刻超出了第2门限T2>T1,则直接认为该条航迹无效。
(3)有效航迹概率

在本次仿真中,总航迹条数为蒙特卡洛仿真次数。
4.2 仿真场景及参数
为设计符合昆虫目标运动特性的仿真场景,基于本团队于河北廊坊实验基地用相控阵雷达采集的昆虫目标回波数据,分析得出昆虫目标的运动轨迹大部分可近似为直线运动,并且对100条昆虫轨迹的平均速度进行了直方图统计,得出轨迹速度大小近似服从均值为4.9 m/s,标准差为2.1 m/s的正态分布。
因此,设计如图8所示的仿真场景,目标做匀速直线运动,初始位置为(10 m,10 m),速度为(5 m/s,5 m/s)。虚假量测是在以正确量测为中心的正方形内均匀产生的,正方形的面积为S=nc/λ,其中nc为虚假量测总数,λ为虚假测量的空间密度,落入两维量测确认区域内的虚假量测数近似服从泊松分布[11],仿真参数如表1所示。
本文首先分析了不同SNR及不同量测噪声下的跟踪精度,同时,为了更好地评估该算法对于起伏目标的跟踪性能,选取2组Gamma起伏模型参数,分析了起伏模型参数对跟踪性能的影响。
4.3 跟踪性能分析
4.3.1 不同SNR下仿真结果分析
采用表1所示的仿真参数,得出在不同SNR下两种算法有效航迹的均方根误差,如图9所示,可以看出,随着SNR的增加,PDAF和PDAF-AI的跟踪误差均逐渐减小,在相同SNR下,相比于PDAF,PDAF-AI的跟踪性能有所改善。
为进一步分析算法性能,本文对同一杂波密度,不同量测噪声下的算法性能进行了对比分析,分析指标为在剔除无效航迹后,相比于PDAF算法,PDAF-AI算法在30~100帧的均方根误差均值的改善值,如表2所示。可以看出,随着量测噪声标准差的增大,性能提升越明显。
4.3.2 不同起伏模型参数下仿真结果分析
由于在实际观测中,不同目标的RCS起伏模型参数是波动的,因此,本文对表1中的两组典型目标起伏模型参数,在SNR均值为9~15 dB情况下的有效航迹概率进行了对比,结果如图10所示。表3所示为PDAF-AI算法在两种参数下的有效航迹改善率,可以看出,当SNR越弱时,跟踪性能提升越显著,同时在不同起伏模型参数下,跟踪性能的提升幅度也略有不同。

图8 仿真场景示意图Fig.8 Simulation scene

表1 仿真参数Tab.1 Simulation parameters
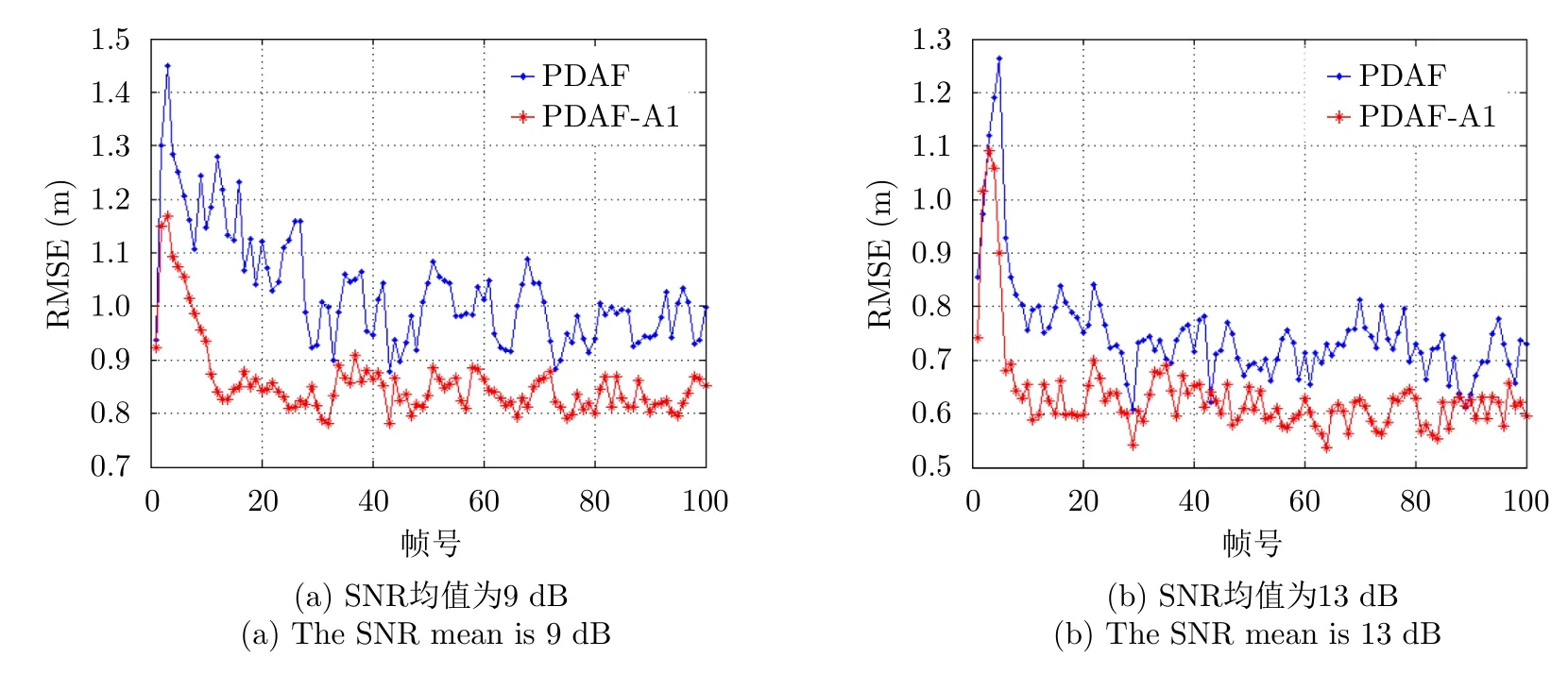
图9 不同SNR下跟踪误差比较Fig.9 Comparison of tracking errors under different SNRs

表2 不同量测噪声下均方根误差均值改善值Tab.2 The improvement of the root mean square error under different measurement noises
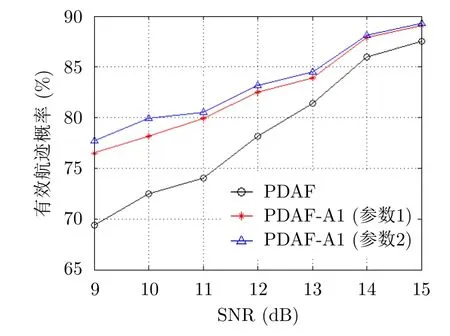
图10 有效航迹概率Fig.10 The probability of effective track

表3 不同起伏参数下有效航迹改善率Tab.3 The improvement probability of effective track under different fluctuation parameters
5 结束语
本文首先基于Ku波段昆虫雷达采集的昆虫目标实验数据,建立了昆虫目标的RCS起伏模型,将其作为先验信息,推导出在高斯白噪声背景下Gamma起伏目标的幅度似然比,然后将其加权到概率数据互联滤波器的关联概率中。基于均方根误差和有效航迹概率对杂波中单目标的跟踪仿真结果进行性能

