基于幅相分离的属性散射中心参数估计新方法
蒋 文 李王哲
(微波成像技术国家级重点实验室 北京 100190)
(中国科学院电子学研究所 北京 100190)
(中国科学院大学 北京 100049)
1 引言
根据目标先验信息数据库建立的方式,合成孔径雷达(Synthetic Aperture Radar,SAR)目标识别可分为基于模板的目标识别和基于模型的目标识别两类[1]。模板数量的有限性限制了第1种方法的应用[2–6],基于模型的目标识别可以避免这个问题[7],采用合适的模型并调整模型参数预测目标在各种姿态及环境下的图像和特征,并将待识别目标的已知图像或特征与其预测图像或特征作对比即可识别目标。属性散射中心(Attributed Scattering Center,ASC)模型参数可精确描述目标散射结构特征且灵活性高,故被广泛应用在基于模型的SAR目标识别中[6]。考虑到从待识别目标的已知SAR图像或回波中提取ASC参数是基于ASC模型的SAR目标识别中的基础步骤,本文主要研究ASC参数估计问题。
ASC参数估计实际上是一个参数优化问题[8],但模型参数多(包含描述ASC几何物理特征的7个参数),给参数估计的高速性和准确性都带来了极大的挑战,为了解决这个问题,已有大量文献进行了相关研究[9–20]。研究方法分为基于图像分割的参数估计方法和基于稀疏理论的参数估计方法。
基于图像分割的ASC参数估计方法通过先将SAR图像分割再分块处理的方式降低了干扰影响并提高了算法速度[9],但该方法中使用近似最大似然法,算法抗噪性能低且不能保证全局最优解[13]。对部分参数降耦合可降低算法复杂度,但在高斯白噪声存在时构造的代价函数维度是频率采样点数与方位角采样点数乘积的平方,当频率采样点数和方位采样点数较高时,算法复杂度高[13];为了实现部分参数的降耦合,位置参数的估计准确度完全取决于除散射幅度以外的其他参数的估计准确度,存在累积误差[13,14]。
基于稀疏理论的ASC参数估计方法通过引入压缩感知领域算法并构造高维联合字典进行参数估计[15],由于模型参数维数较高,构造的高维联合字典将消耗较多系统资源[16]。通过分别构建包含位置信息与方位属性参数信息的2个低维字典可降低系统资源[18],但这种字典降维方法只适合相对带宽较小(0.06)的情况,当相对带宽增大时,该方法失效;且此时在估计频率与方位依赖参数时构造的字典维度分别为,不满足完备字典维度条件,使用正交匹配追踪(Orthogonal Matching Pursuit,OMP)算法不合理[19]。通过引入增量式稀疏贝叶斯学习(Incremental Sparse Bayesian Learning,ISBL)算法也可降低系统资源,但不能保证得到全局最优解[20]。
综上所述,通过基于图像分割的参数估计方法可提高参数估计速度并降低干扰影响[10],但不能保证求解精度[19],改进的方法代价函数维度和累计误差大;基于稀疏理论的参数估计方法虽然可以在一定程度上避免图像分块带来的误差,但字典的高维度特性限制了该方法的使用,改进方案的适用范围有限且不能保证全局最优解[18,20]。
为提高ASC的参数估计速度并抑制杂散影响,首先提取多个ASC再分别估计各个ASC的参数,但单个ASC的参数估计问题仍然是一个高阶问题,复杂度高。考虑到单个ASC的幅度和相位相关项可分离,本文提出基于幅度相位分离的ASC参数估计思想,根据幅度数据估计幅度相关参数,根据相位数据估计相位相关参数,将算法时间复杂度降低了1个数量级。该思想还可降低累积误差并保证相对带宽较大情况下参数估计的可行性。为了保证参数估计的准确度,引入迭代半阈值(Iterative Half Thresholding,IHT)算法估计参数值[21,22]。通过依次估计各ASC的参数最终可识别目标上所有散射结构并判断其位置分布。使用所提方法对仿真数据和实测数据以及MSTAR数据集进行ASC参数估计,估计效率及精度较已有方法有明显提高,证实了本文所提方法的有效性。
2 属性散射中心模型
2.1 ASC模型概述
根据几何绕射理论(Geometrical Theory of Diffraction,GTD)和物理光学理论,考虑雷达回波对频率和方位角的依赖关系,ASC模型为[9,23–25]


2.2 幅度相位分离的属性散射中心模型
分析式(2)可知单个ASC的幅度与相位相关参数不相关,根据该思想对式(2)进行改造


表1 简单散射结构α取值表Tab.1 Discrimination of canonical scattering geometries from α

表2 不同L和α对应典型散射结构Tab.2 Discrimination of canonical scattering geometries from L and α
3 基于幅度相位分离的属性散射中心参数估计方法
3.1 迭代半阈值算法引入
如式(1)所示,在高频电磁区,雷达目标的回波信号是少数几个ASC的叠加[16],ASC参数估计实际上是一个多维参数优化问题[8],为保证参数估计的准确性,引入IHT算法[21,22]
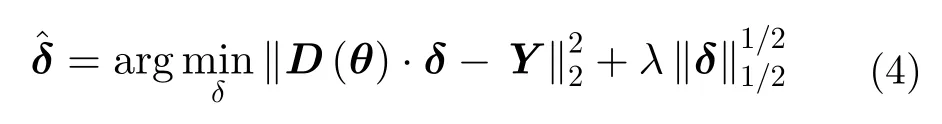
3.2 基于幅度相位分离属性散射中心模型的字典构造方法
由2.2节和3.1节可知,使用Ef(Ep)的值与IHT算法可估计。即

其中,Df是由幅度相关参数构造的幅度字典,Dp是由相位相关参数构造的相位字典,和分别是求解和时的稀疏系数向量,和是它们的估计值。
根据式(3)构造的Df和Dp分别为

其中,abs(·)表示取幅度操作,phase(·)表示取相位操作。从式(7)–式(11)可知Df和Dp的维度为则Df和Dp的维数为M(N1+N2+N3),N3<<N1,若不使用幅度相位分离思想,则D的维度为MN1N2[15],前者比后者低1个数量级,因此幅度相位分离思想可节约参数估计的系统资源和时间复杂度。
3.3 基于幅度相位分离思想的属性散射中心参数估计流程
对于回波中包含的多个ASC,本文提出的参数估计方法如图1所示,具体步骤如下:
步骤1 小转角时利用傅里叶变换(FT)算法成像,大转角时采用复数后向投影(Back Projection,BP)变换成像,从图像中获取参数x和y的大致范围;
步骤2 采用分水岭算法[9]从图像中分割出N个ASC;
步骤3 FFT得到各ASC的回波数据;

图1 本文所提ASC参数估计流程图Fig.1 Flow chart of the method for estimation of ASC parameters proposed in this paper
步骤4 使用3.2节介绍的方法构造字典Df和Dp;
步骤5 将各ASC对应的回波数据向量化构成向量Yi,i=1:N,令t=1;
在全面深化改革时期,随着法治进程的加速,执政党依法执政意识逐渐强化,人民的法治观念基本得以确立,宪法适应性有所增强,但在宪法适应性机制与实践方面仍存在不足之处。
步骤6 分别估计各ASC幅度相关参数和相位相关参数:
(1)利用IHT算法基于Df和Ef的值;
(3)利用IHT算法基于Dp和Ep估计{xt,yt,phase(At)}的值。
步骤7 判断t≤N是否成立,若成立则转到步骤6继续执行,否则进行下一步;
步骤8 根据各ASC估计参数识别其对应散射结构类型。
4 实验结果与分析
4.1 仿真实验
仿真实验分为3部分:比较D和Df与Dp的维度;在IHT算法的条件下分别基于2种字典求解单个ASC参数,并根据运算速率和准确性来证明幅度相位分离思想的优越性;最后分别使用传统方法[15]和本文所提方法估计多个ASC参数并比较2种方法的速率和有效性,各个ASC对应的典型散射结构的识别可根据L与实现。仿真参数为:中心频率9 GHz,带宽2 GHz,成像积累角3°,采样点数50×120。
4.1.1 高维联合字典与幅度相位分离字典维度对比
在上述仿真参数条件下取各参数范围如表3所示,由此可得D的维度为2.8754e+12,Df和Dp的维度为1.9223e+09,后者比前者低3个数量级,节省了系统资源,其对参数估计速率的影响见4.1.2节。

表3 仿真参数取值Tab.3 Values of the simulation parameters
首先根据表3中各参数取值分别构造D,Df与Dp,然后在表3所示参数范围中随机选取100组单个ASC参数构造100组雷达回波,基于IHT在两种字典条件下分别估计各ASC的参数,两种条件下的估计速率和准确性见表4。准确性由均方误差(Mean Square Error,MSE)评估,MSE的定义为

表4 两种字典构造方法性能对比Tab.4 Performance comparison of the two dictionary construction methods

基于两种字典的单个ASC参数估计对比如表4。
从表4中可以看出,在估计单个ASC参数时,使用幅度相位分离思想可以大大降低参数估计时间,且估计精度基本不变,证明了幅度相位分离思想的优越性。
4.1.3 基于幅度相位分离思想的属性散射中心参数估计方法性能验证
对目标上存在多种散射结构的情况,分别使用传统方法和图1中所提方法进行参数估计。仿真3个ASC的情况,估计结果如表5和表6所示,其中S1,S2,S3表示3个ASC,运算速率和准确性如表7所示,根据表2对S1,S2,S3对应散射结构的识别结果见表8。
从表7可以看出本文所提方法在运算速率和估计精度上都优于传统方法,为了更直观地展示算法准确度,将分别由原始参数重构的SAR图像(图2(b))和由2组估计参数重构的SAR图像(图2(a),图2(c))进行对比,可以看出由本文ASC参数估计方法得到的参数结果重构的SAR和原始设置参数重构的SAR图像更加接近(绿色方框),进一步说明了本文所提方法的高估计精度。对比观察表8和图2,圆柱及帽顶型散射结构清晰可见,证实了由ASC参数识别其对应散射结构的有效性。
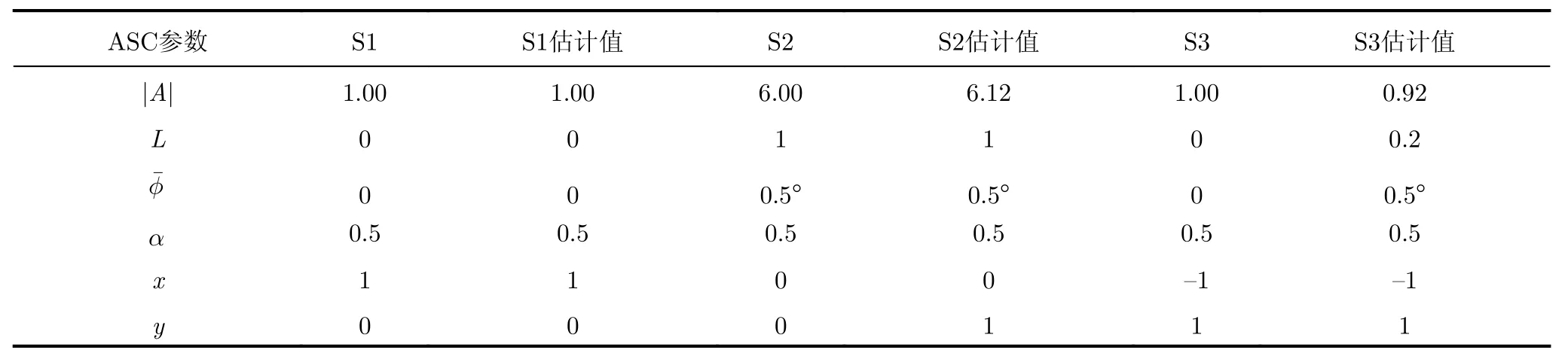
表5 基于传统方法的多个ASC参数估计结果Tab.5 Estimation results of ASCs parameters using traditional method

表6 基于本文方法的多个ASC参数估计结果Tab.6 Estimation results of ASCs parameters using the method this paper proposed
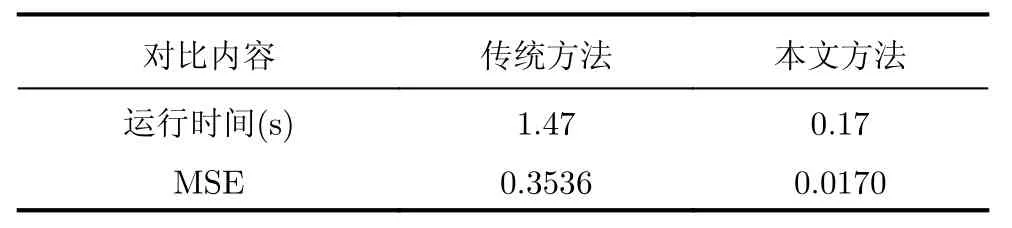
表7 2种ASC参数估计方法性能对比Tab.7 Performance comparison of the two ASC parameters estimation methods

表8 3个ASC对应散射结构识别结果Tab.8 Recognition results of the scattering geometries corresponding to the three ASCs
4.2 ISAR数据验证
使用微波光子雷达系统进行ISAR成像,雷达中心频率为15 GHz,带宽2 GHz,发射线性调频信号,脉冲宽度为50 μs,平台旋转速度为10°/s,平台和收发天线之间的距离为10 m(接收端连接150 m延迟线)。观测目标为1个三面角反射器和1个用铝箔包裹起来的羽毛球筒,羽毛球筒长度为37 cm,底边直径为6.7 cm,2个目标分别放置在转台对角线两端,距离向距离为48 cm,方位向距离为30 cm。成像场景如图3(a)所示,选取方位向持续时间为0.3 s的数据进行成像,成像结果如图3(b)所示,采用本文所提方法估计的ASC参数结果如表9所示,根据参数估计结果判定的散射结构如表10所示。将表10和图3进行对比并结合目标真实几何和物理特征,可以看出本文所提方法能准确估计ASC参数。将由估计得到的ASC参数重构ISAR图像展示如图3(c),其与图3(b)(原始ISAR图像)的高相似性直观地证明了本文所提算法的有效性。
4.3 MSTAR数据验证
下面通过MSTAR[26]T72坦克目标实测SAR图像数据进一步验证本文所提方法的有效性。MSTAR数据为美国DARPA/AFRL MSTAR项目提供的实测SAR地面目标数据,是迄今公开较为完备,评价SAR ATR算法性能较为标准的数据。数据由聚束SAR获取,分辨率为0.3 m,图像切片大小为128×128像素,本次试验采用的是编号为HB05649.016的T72 SAR图像。T72的数据录取俯仰角为17°,方位角变化范围为[78.57°,82.97°],车体长6.41 m,炮向前时炮筒伸出长度3.035 m[27]。

图2 原始算法与本文算法性能比较图Fig.2 Performance comparison of the traditional method and the method this paper proposed

图3 实验场景及成像结果Fig.3 Experimental filed and ISAR images
图4为坦克的光学图像,图5(a)为本次试验中用到的SAR图像,去零去窗后的SAR图像如图5(b)所示,使用分水岭法对图5(b)进行分割,分割结果如图5(c),其中每种相同颜色连接起来的区域代表1个ASC,共包含16个ASC,各个ASC在目标上的分布如图5中的数字所示。由所有ASC估计参数结果重构的SAR图像如图5(d)。

表9 ASC参数估计结果Tab.9 Estimated parameters of the 2 ASCs
16个ASC的参数L与估计值见表11,由表中可知坦克炮筒伸出车体的估计长度为2.67 m,文献[18]中的估计结果为2.653 m,和实际的3.035 m相比本文的估计结果更准确。根据表1和表2的散射结构判定准则对各个ASC进行判定,结果如表11的第4行和第8行所示。

图4 T72光学图像Fig.4 T72 optical image

表10 ASC对应散射结构判定结果Tab.10 Recognition results of the scattering geometries corresponding to the 2 ASCs

图5 多幅T72 SAR图像Fig.5 Various T72 SAR images
根据表11第4行和第8行将各ASC对应的散射结构类型标记如图6所示,其中左上角是图5(c)中的分割图像,左下角是图例,右侧是图5(c)中16个ASC对应的不同散射结构在目标上的位置分布示意图。

表11 ASC参数估计结果及对应散射结构判定结果Tab.11 Estimation results of the ASCs parameters and the recognitionresults of the scattering geometries corresponding to these ASCs
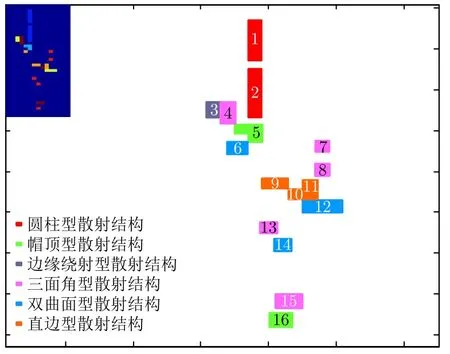
图6 各个ASC对应散射结构位置分布图Fig.6 Estimated position distribution map of scattering geometries corresponding to the ASCs
由图6可知,圆柱类型散射结构主要为坦克炮筒位置,顶帽类型散射结构主要在坦克车体中间车盖和车尾位置,边缘绕射类型散射结构主要分布在车盖附近位置,三面角类型散射结构主要分布在坦克车盖附近和车体内部位置,双曲面类型散射结构主要分布在坦克车体中间的两侧和车盖附近位置,直边类型散射结构主要位于坦克车体中间位置。
由根据仿真数据和实测数据以及MSTAR数据集的实验结果可以看出,基于幅度相位分离的字典构造方法能够大幅度节约系统内存,提高参数估计速率,通过IHT算法能够较准确地估计目标上主要ASC参数从而识别目标上的基本散射结构。
5 结论
针对ASC参数估计问题,为了提高参数估计速度,本文先分割图像提取多个ASC再逐个估计ASC参数,考虑到单个ASC幅度相位相关项可分离,提出幅度相位分离的ASC参数估计方法,将参数估计的时间复杂度降低了1个数量级,节约了系统资源并提高了参数估计速率,引入的IHT算法提高了参数估计的精度。根据各个ASC的参数估计结果可识别目标上散射结构并分析其分布位置。从仿真数据、实测数据以及MSTAR数据集得到的参数估计的高效性和高准确性方面,验证了本文所提方法的有效性。

