破碎区准备巷道围岩耦合控制研究

王 力

（山西霍尔辛赫煤业有限责任公司，山西 长治 046600）

煤层由于在成煤作用时期受到诸多高强度的地质作用，煤层内部裂隙发育、强度较低[1]。在受到巷道采掘扰动后，若支护强度不足，极易造成“支护体-围岩”共同承载结构稳定性下降，巷道围岩破碎。在原岩应力重新分布之下，造成巷道整体失稳，巷道表面收敛量剧烈、巷道围岩失稳，严重影响巷道的正常使用[2,3]。采（盘）区准备大巷，承担着整个采（盘）区内的材料、设备、人员、煤流以及风流的运输与传递，对于矿井的生产与安全有着直接的影响与控制作用。若大巷围岩破碎，结构体失稳，则严重影响采区作业，不利于矿井的高效安全生产。针对大巷以及采（盘）区准备巷道的破碎围岩支护问题，众多煤炭科技工作者进行了研究与探索，但各个煤矿煤层围岩地质条件千差万别，故应当结合矿井实际工程地质情况，设计有针对性的采（盘）区巷道支护参数与形式，提出经济上合理，安全上可靠的巷道围岩控制方案。

1 工程概况

霍尔辛赫煤矿东辅运大巷为南北走向，布置在3#煤层中，无其他采掘煤层影响。巷道开口位置南边为东辅运大巷已掘巷道，东侧60m处为未施工的东回风开拓大巷，西侧60m处是主运大巷已施工巷道，北侧为未采掘实体煤区域。东辅运大巷掘进范围内3#煤层厚度5.6～5.8m，平均5.65m，煤层倾角3°～18°，平均10°，煤层层理中等发育，煤层节理中等发育。该煤层赋存于二叠系山西组地层中下部，为陆相湖泊沉积，结合东辅运大巷掘进范围内矿井3181号钻孔及主运大巷揭露煤层结构情况，掘进范围内煤层厚度稳定，局部有1～2层块状夹矸，煤层普氏系数为0.3～0.5。东辅运大巷掘进范围内地面标高+913.7～ +941.7m，井下标高+460～ +500m，工作面最大埋深481.7m，最小埋深413.7m。巷道顶底板厚度与岩性见表1。东辅运大巷掘进范围内无大型地质构造，无断层与陷落柱揭露，东辅运大巷掘进范围内地质条件与水文地质情况简单。

东辅运大巷巷道设计断面为矩形，设计毛断面为（宽）5.5×（高）5.6m，净断面为（宽）5.2×（高）5.3m，掘进时大巷沿底掘进，采用全断面一次掘进方法。

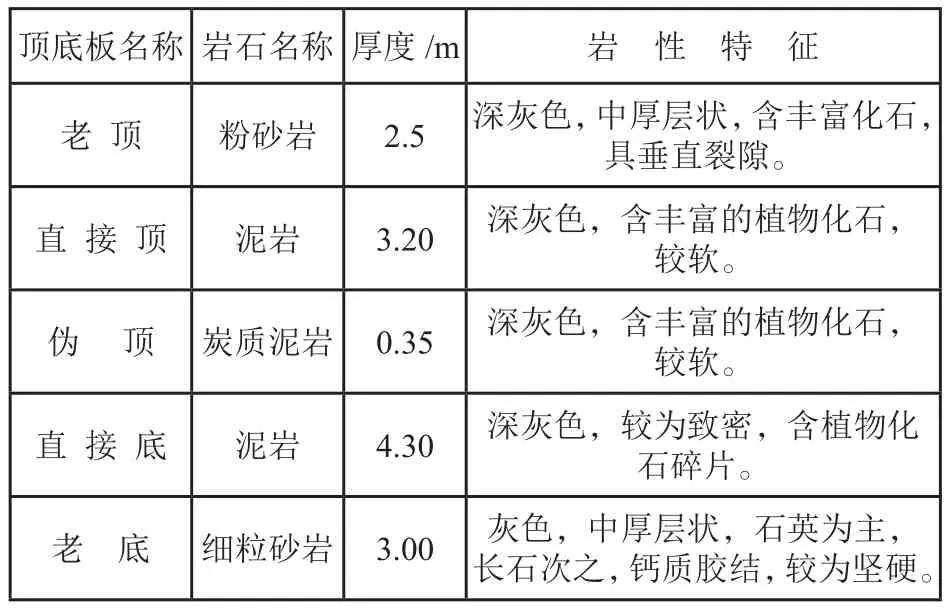
表1 煤层顶底板特性表

2 破碎围岩巷道破坏特征

由于巷道掘进高度小于煤层厚度，同时煤层上覆伪顶、直接顶为强度较弱的泥岩与炭质泥岩，在受到掘进扰动后，形成围岩破碎巷道。此时巷道顶板与两帮呈散体状态，极易形成平衡散体拱结构，可依据秦巴列维奇理论建立如下力学模型，见图1。

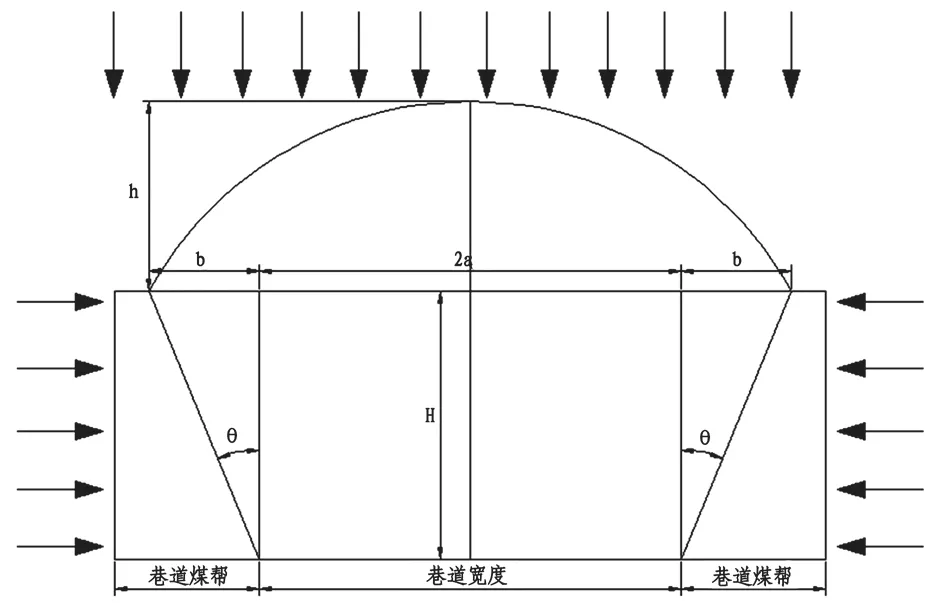
图1 秦巴列维奇理论力学模型图

由图1可知，巷道受到三向压力影响，由于顶板形成散体拱结构，产生“卸荷”效应，对巷道产生保护效应。巷道两侧受到水平应力的影响，破碎围岩若无有效支护则自行垮塌，形成煤壁片帮等现象。因此，必须对巷道顶板最大破坏深度h以及巷道两帮最大垮落深度进行预计，以防止巷道围岩失稳。计算公式见式（1）、（2）、（3）。

式中：

H-巷高，取5.6m；

θ-煤塌陷角，°；

φ-煤内摩擦角，取28°；

式中：

a-巷宽，取2.6m；

RC-煤单轴抗压强度，取5.2MPa。

带入公式可得，巷道两帮最大破坏深度b为3.4m，巷道顶板最大冒落高度h为11.5m。

3 巷道优化支护形式及效果

考虑上述理论计算中的两帮以及顶板破坏深度较大，单纯采用普通的“锚杆-锚索-喷浆”联合支护措施，已经不能满足巷道支护强度要求，故考虑长短锚索结合的全锚索支护形式，即一次支护为短锚索支护，二次加打长锚索支护，最终对巷道表面进行喷浆。设计支护参数见表2。巷道支护断面图见图2。

表2 巷道优化支护参数

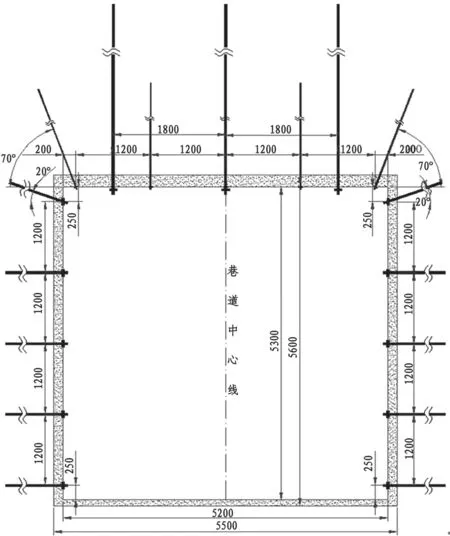
图2 巷道支护断面图

4 巷道失稳预警阈值计算

采用弹塑性力学中的卡斯特纳理论，对东翼盘区辅运大巷道各种支护情形下破碎围岩最大位移进行计算。由弹塑性力学可知，在宏观受力剖面上，可将巷道围岩破坏视为以圆形塑性区渐进发展，同时，巷道水平应力在350m之下可近似视为与垂直应力相等。破碎围岩力学原理见图3。

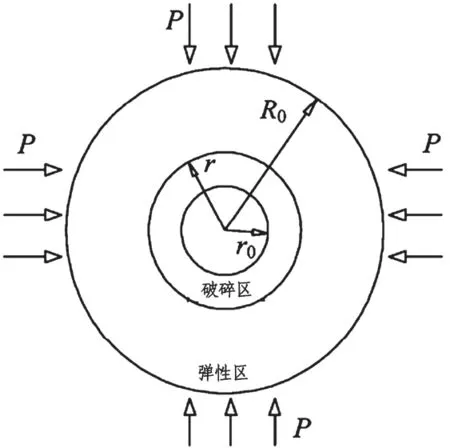
图3 破碎围岩受力模型图

4.1 巷道一次支护时机

巷道围岩掘进后无支护时，巷道围岩失稳破碎时的最大位移可按式（4）计算[4]。

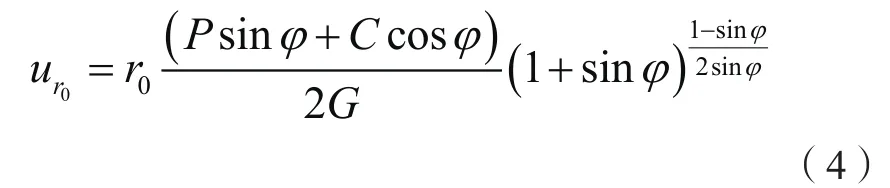
式中：

-巷道围岩失稳破碎时的最大位移，mm；

r0-矩形巷道对角线之半，取4.0m；

P-大巷原岩应力，P=γH，其中，γ为上覆岩层平均容重，取24.5kN/m3，H为覆岩最大埋深，取481.7m；

φ-围岩平均内摩擦角，实验测得为28°；

G-围岩体积模量，实验测得为2.45GPa；

C-围岩粘聚力，取1.46MPa。

带入计算可知，巷道围岩掘进后无支护时，巷道围岩失稳破碎时的最大位移为6.94mm，为考虑一定的安全系数，取6mm。

4.2 巷道二次支护时机

巷道一次支护后，由于支护强度不够，必然会导致进一步破坏，塑性区会进一步发展，但此时必须将一次支护强度P1纳入考虑范围，但由于在一次支护后P1必然受到诸多人为因素的影响，必须对此进行实测，故此处不做具体计算，只给出计算方法，见式（5）。

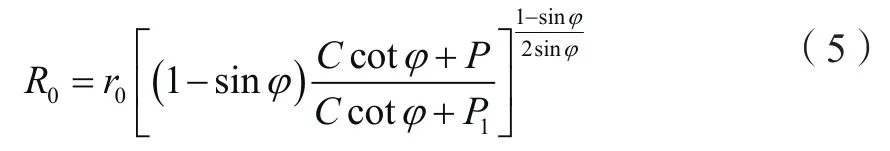
式中：

R0-一次支护后塑性区发展范围，m；

P1-一次支护强度，MPa。

二次支护时最大失稳位移可按式（6）进行计算。

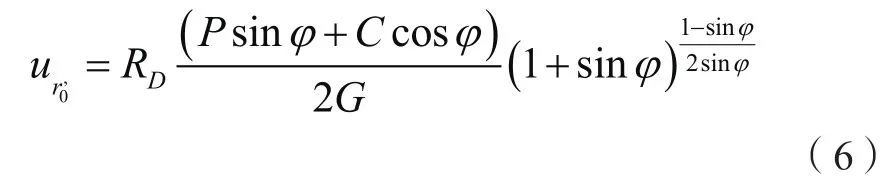
式中：

-一次支护后巷道围岩失稳破碎时的最大位移，mm；

RD-一次支护完全失稳距离，即短锚索长度与r0之和，9.0m。

带入计算可得，一次支护后巷道围岩失稳破碎时的最大位移为15.6mm，考虑一定安全系数，取15mm。

故可在巷道掘进完成后，监测巷道表面位移计，在巷道顶底板相对移近量或两帮移近量达到6mm之前，必须进行一次支护。在一次支护完成后，现场实测一次支护强度，带入式（5）计算得到一次支护失稳位移，在巷道顶底板相对移近量或两帮移近量达到该值之前，必须进行二次支护。巷道全部支护完成后，在巷道顶底板相对移近量或两帮移近量达到15mm之后，必须采取相应紧急措施，例如围岩注浆等措施，以维护巷道围岩的稳定性。

4.3 巷道支护效果监测

为监测巷道支护效果，在东辅运大巷掘进支护完成后，进行了钻孔窥视，对巷道围岩状况进行了观测，见图4，对巷道表面位移进行了监测见图5。

图4 巷道表面0～2m钻孔窥视结果

在图4中可以看出，巷道覆岩0～2m范围之内并未出现明显的纵向破坏裂隙，也未出现明显的横向层理发育，岩层整体保持稳定，可见新的“全锚索”支护参数可以有效保证巷道围岩稳定。

由图5巷道表面位移变化图可以看出，东辅运大巷顶底板最大移近量为4.9mm，两帮移近量最大为2.1mm。巷道变形量均在巷道安全预警阈值之内，再次证明新的“全锚索”支护参数可以有效控制巷道表面位移，保证巷道安全使用。

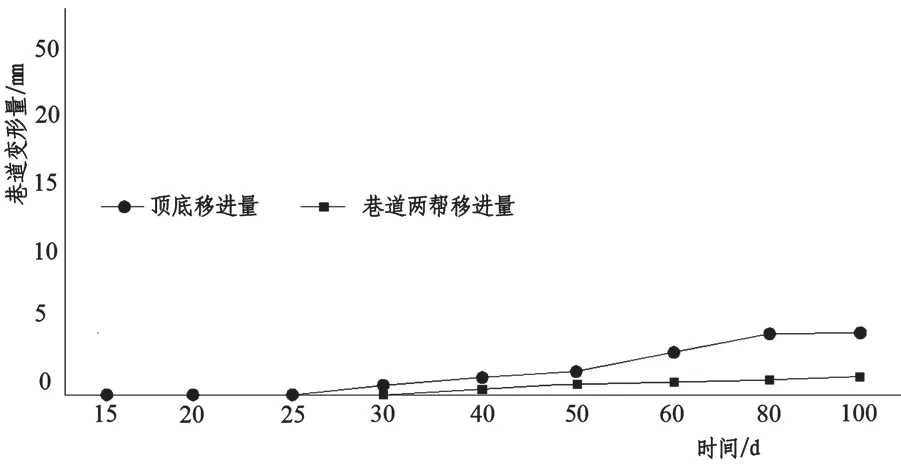
图5 巷道表面位移随时间变化图

5 结论

采用秦巴列维奇理论，确定两帮最大片帮深度为3.4m，巷道顶板最大冒落高度为11.5m。采用卡斯特纳理论，计算了东翼盘区辅运大巷道围岩最大失稳位移为6.94mm，二次支护时最大失稳位移为15.6mm。考虑一定安全富余量，得出巷道失稳预警阈值，当巷道完全支护完成后，围岩变形量为15mm，巷道完全破坏，必须采取紧急措施。设计了巷道支护参数，在现场应用后，巷道表面0～2m围岩稳定，东辅运大巷顶底板最大移近量为4.9mm，两帮移近量最大为2.1mm，满足预警阈值要求，巷道支护方案起到了作用。