交通流动态扰动下的区域交通信号协调控制

魏永涛 高原 孙文义 王秀蒙

随着机动车保有量的增加,城市交通拥堵现象日益严重,高峰期部分路段或区域常呈现过饱和状态.与此同时,由于不同区域交通分布不均匀,导致部分道路资源浪费.目前,大部分交通信号灯配时控制策略都针对非饱和交叉口,当道路处于过饱和状态时,路网交通效率显著降低.另外,区域路网的信号灯协调优化配时研究较少,尤其过饱和区域路网交通信号控制仍是公开的难题,急需寻求智能优化控制方法.

针对过饱和区域交通信号灯优化问题,文献[1]提出一种能平衡车辆数量增长率的优化配时算法,并基于队列增长给出了过饱和交通流条件下的交通信号最优等式,即队列增长等式以及最小化区域交通队列增长等式,有效避免了特定路段车辆数量过多造成的排队溢出现象.文献[2]提出基于边界需求控制和区域网络内部平衡的过饱和区域主动控制模型,给出了基于边界目标函数和内部信号控制的双层规划优化方法,提高了区域路网的通行能力.文献[3]提出了一种基于区域路网固有属性宏观基本图的过饱和区域控制优化模型,建立了边界控制信号和内部控制信号目标函数的双层规划优化,设计了基于BP 神经网络的自适应动态规划模型.但是基于单个过饱和路口模型对多个路口叠加建模,不能充分保证跨区域交通的协调性.

为提高城市交通区域网络协调控制性能,人们做了很多有益的探讨,其中模型预测控制[4]即是常用的区域信号灯协调控制方法.Aboudolas 等[5]提出了基于滚动优化的交通信号灯协调控制策略.Lin提出了一种非线性宏观交通模型,并以此为基础设计了一种全网交通信号模型预测控制方法[6],将优化问题归结为一个混合整数线性规划问题来求解[7].此后,Zhou 等[8]提出一种新的模型预测方法,将机会约束应用到城市交通信号灯控制之中.由于大型交通网络高度复杂,上述集中式模型预测控制方法并不适合大型区域信号灯协调控制,必须采用分布式控制方法.Tettamanti 等[9]提出了一种基于模型预测控制的分布式交通控制方法,把整个城市交通网络分解成若干小的子区域,每个子区域看作一个独立控制和运行的智能体,多个智能体之间通过网络互联、共享资源,从而实现全路网信号灯协调控制.文献[10]提出了一种区域路网信号灯协调控制的多智能体模型预测控制框架,利用拉格朗日对偶原理处理智能体间的耦合约束.De Oliverira 等[11]也针对线性动态城市区域交通流给出了多智能体分布式控制模型,将集中式模型预测控制问题分解成几个子问题,由分布式智能体来求解.在此基础上,Camponogara 等[12]考虑输入–输出约束,提出线性动态交通网络模型预测控制的分布式优化算法.文献[12]结合周边控制和路径诱导执行器,提出了非线性模型预测控制方法,提高了城市路网的机动性.Sirmatel 等[13]对上述非线性模型加以改进,提出一种用于协调信号拆分控制的分布式协调模型预测控制方法.但该方法计算较为复杂,为此文献[14]将大型区域路网划分成多个子区域,将交通流在多个子区域之间进行存储转发[15],采用文献[16]的存储–转发方法描述路网交通流变化,规避了模型需引入二进制变量来描述信号灯处于红绿状态的问题,并提出一种计算简便的分层模型预测控制算法,便于实现区域信号灯的最优协调控制.

值得指出的是,文献[15]未考虑交通流变化扰动对区域交通协调控制的影响,其方法不够实用.为此,本文在文献[15]的基础上,考虑交通流的动态变化,通过改进存储–转发机制,建立了更贴近实际排队长度的区域交通模型,进而提出一种区域交通信号协调控制的分层优化求解的模型预测控制方法.

本文结构安排如下:第1 节,考虑交通流的动态特性,引入存储–转发的思想,建立区域交通模型;第2 节,提出模型预测优化模型;第3 节,将优化模型进行分层,求解出控制变量最优解,并给出区域交通的控制算法;第4 节,给出本文算法的仿真分析;第5 节,对本文内容进行总结.

1 区域交通建模

为了简化表示,城市区域交通可以被定义为一个有向图.其中,节点代表交叉路口i,弧线代表交通流r.不失一般性,假设区域中交通流r1转弯率为τr1,r2和饱和流率Sr1是可测的常数.另外,交叉路口i中相位p的有效绿灯时间gi,p,损失时间Li和周期时长Ci满足其中Fi是允许车辆离开交叉路口i的相位集合.为了协调整个区域,对于任意一个交叉路口i,都有Ci=C成立.

考虑从交叉路口i流向交叉路口的单交通流j(见图1(a)),对于下一个时刻k+1 末,交通流r上的车辆排队长度等于在k末,路口剩余的排队长度加上到来的车辆流量Ii,r,减去在有效绿灯时间内流出的流量Oi,r.图1(b)表示区域中交通流linkr只有外界输入流量.

图1 交通流r 的交通动态图((a)交通流无外界输入;(b)交通流有外界输入(虚线))Fig.1 Traffic dynamics ((a)Traffic without input;(b)Traffic with inputdotted lines)

可以通过下面的离散时间模型建立r的交通流动态模型.

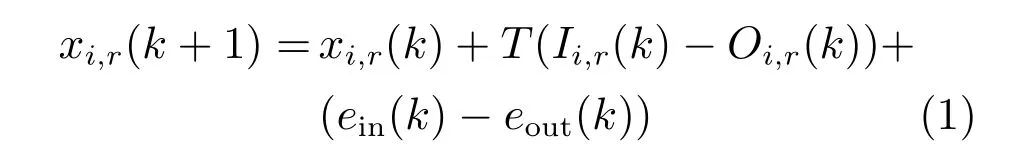
其中,xi,r(k)表示在第k个信号周期开始时,位于i交叉路口的交通流r上的车辆数量.xi,r(k+1)表示在第k个信号周期结束时(第k+1 个信号周期开始时),位于i交叉路口的交通流r上的车辆数量.Ii,r(k)和Oi,r(k)表示交通流r的流入流量和流出流量.较之文献[15]中采用经验值的做法,用ein(k)表示在第k个信号周期内由路口进入交通流r的车辆数量.eout(k)表示在第k个信号周期内由路口离开交通流r的车辆数量.令ei,r(k)=ein(k)−eout(k)称为交通流的扰动,比如路边停车位的车辆.由此分析可知ei,r(k)是一个随机变量.T表示控制间隔.本文假设控制间隔T为一个信号周期C.

假设交叉路口i和相邻交叉路口j之间的偏移量等于零.针对交通流r,流入的车辆来自于路口j中的交通流w1,w2,w3,然而并不是交通流w1中所有的车辆都会流入r,只有左转车流最终会驶入交通流r,假设左转车辆占整个交通流w1的比例为τj,w1;i,r,称之为转弯率,即τj,w1;i,r表示从交叉口j的w1交通流转入到交叉口i的r交通流的转弯率.同理交通流w2中只有直行车辆流入交通流r,交通流w3中只有右转车辆流入交通流r.故r的流入流量Ii,r(k)=τj,w1;i,rOj,w1(k)+τj,w2;i,rOj,w2(k)+τj,w3;i,rOj,w3(k).即交通流r的流入流量Ii,r(k)可以写成:

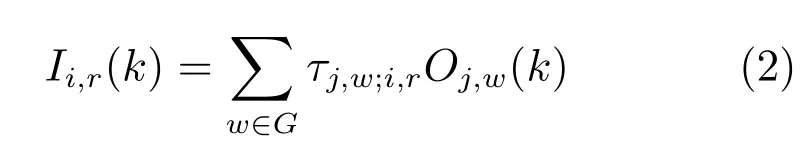
其中,G表示交叉口j中流入交通流r的交通流集合(对于交通流r来说,G=w1,w2,w3).τj,w;i,r表示从交叉口j的w交通流转入到交叉口i的r交通流的转弯率.

对于流出流量,文献[15]将其表示为饱和流率(常量)乘以绿灯时间,但在实际的交通中,并不是每一时刻的车流量都是以饱和流率流出的.所以结合实际交通情况,本文把实时检测到的交通流量和绿灯时长作为控制变量.这样建立的模型更符合实际交通.即对于流出流量Oi,r(k),它是由相位的绿灯时间gi,p(k)和单位周期内的释放的车流量q决定的.即交通流r的流出流量Ii,r(k)可以写成:

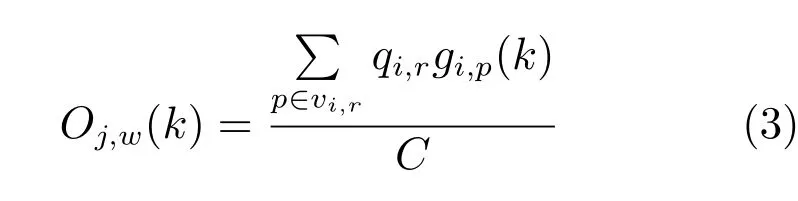
其中,vi,r代表允许交通流r通行的相位集合.qi,r称为交通流r的交通流量.

以一天的交通流量为例进行分析,早上7 点到9 点属于上班高峰期,下午5 点到7 点属于下班高峰期.很大程度上高峰期车流量可以以饱和流率驶离路口,但是在一天中的非高峰期,车辆通常不能按照饱和流率通行.对一周内交通流分析,周一到周五工作日的交通流量和周末的交通流量特性肯定不同,所以仅依靠饱和流率计算车辆的流出量不够准确.智能交通系统中,可以实时检测车流量,这为车流量的取值提供方便.如果将交通流考虑成时变量,处理排队长度优化问题会很复杂,所以本文将仿真一个仿真周期内的交通流量平均值作为整个仿真周期的交通流量,即在每一个仿真周期内交通流量为常数.但是每个仿真周期开始时,会更新交通流量的值,交通流量的大小随着仿真周期的变化而变化,这也能体现交通流的动态特性.

据上述分析,本文把ui,p(k)=qi,rgi,p(k)作为整体控制变量.将式(2)和式(3)及ui,p(k)=qi,rgi,p(k)代入式(1)得:

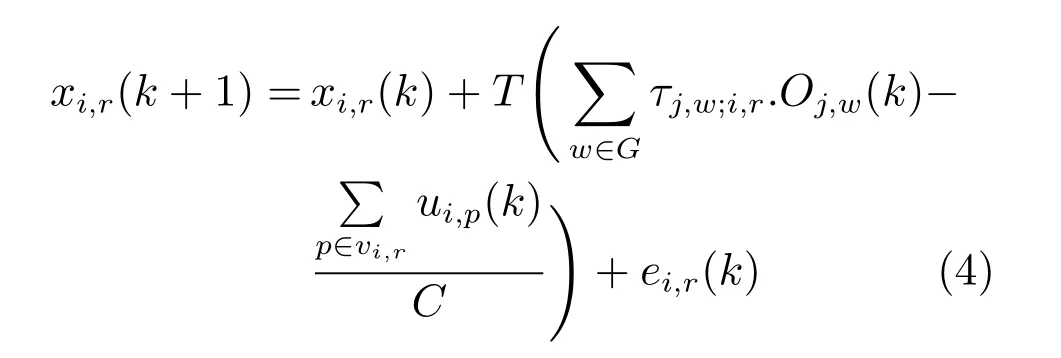
根据式(3)中Oj,w(k)的定义,式(4)中的Oj,w(k)可以写成以及T=C.所以式(4)可以写成:

然后,整个区域都应用式(5),可得到整个区域的离散时间状态空间表达式:

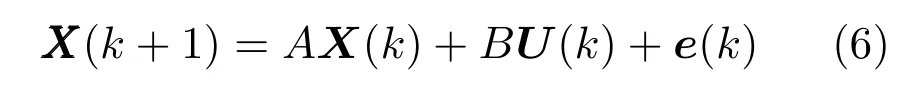
另外,若区域中交通流只有外界输入流量(见图1(b)),则式(2)和式(4)必须写成如下的形式:

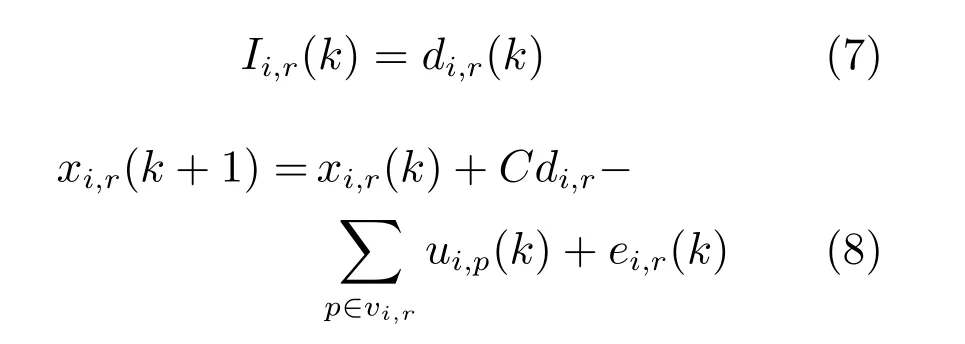
其中,di,r代表i交叉口进入流r的交通需求.为了简化,假设di,r已知.然后,式(6)可以写成:

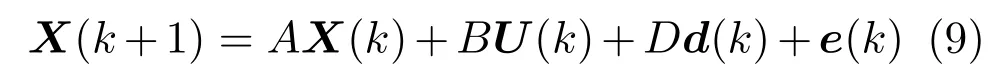
其中,X(k),U(k),d(k),e(k)分别表示状态向量、控制向量、需求向量和扰动向量,且d(k)是常数向量,e(k)是一组随机数组成的常数向量.状态矩阵A为单位矩阵,B是控制输入矩阵,D是需求矩阵.值得注意的是一些网络特性(如拓扑结构、饱和流率、转弯率)都包含在输入矩阵B中.

2 区域交通分解和优化目标

2.1 动态子区域的划分

随着城市建设的发展,城市空间结构和城市功能有了新的变化与发展,而不同的布局结构和功能对交通需求是不一样的,由此造成的交通流分布形态也是不一样的,不同的交通流分布形态对交通诱导与控制的要求是不一样的.因此要实现有效的交通控制,应该根据城市空间和功能的发展变化来对整个交通络系统进行分区.但是值得注意的是,许多资料中显示,系统结构或模型的分解在大规模复杂系统的协调和控制方面都存在先决条件.因此,为了控制和优化的目的,在接下来的部分引入网络分解策略.

为保证控制小区内各路口间协调合作,疏导拥挤交通流,将拥挤区域与临近稀疏路口划为同一个小区,以便于路口间信号协同配时.基于上述思想,本文主要以排队比值的原则划分子区,具体原则如下:

当相邻交叉路口之间的路段距离较短或者交通需求较高,即排队比值较小时,通过关联后实行协调控制,可降低排队溢出而造成交通拥堵的风险.最大可能存在的车辆数与路段堵塞车辆数比值称之为排队比值:

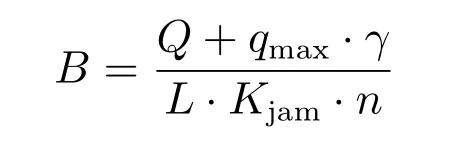
式中,Q表示相邻两个交叉口之间的路段存在的最大交通流量;γ表示相邻交叉口路段交通流量的波动系数;L为车队长度,Kjam表示阻塞密度,n表示车道数.

本文定义相邻交叉口的排队比值关联度为:

所以,从排队比值的角度,可以通过确定IB,来合并交叉路口.

对于城市交通网络,每个交叉口和流入的交通流都可以看成一个子区域.分解区域的依据是能保证优化问题相对应的每个子区域考虑和相邻子区域的所有独立性.因此,每一个子区域Si ∈S包括一个中心交叉口i ∈I和流入的交通流,其中S为子区域集合,I为中心交叉口集合.图2 就是区域分解的例子,可以看出交叉口1 和交通流x1,x2,x3组成子区域S1.图2(b)是对应图2(a)中基准网络的分解示意图.

2.2 优化目标

作为工业过程中最通用和最有效控制技术,MPC 被广泛用于解决大型多变量约束控制问题.MPC 的基本原理是选择一个未来控制行动的序列,解决有限层约束最优控制问题.在每一步,只实现第一个元素的优化计算控制序列.然后,通过样品改变时域大小,这样由测量的新信息重复整个过程.

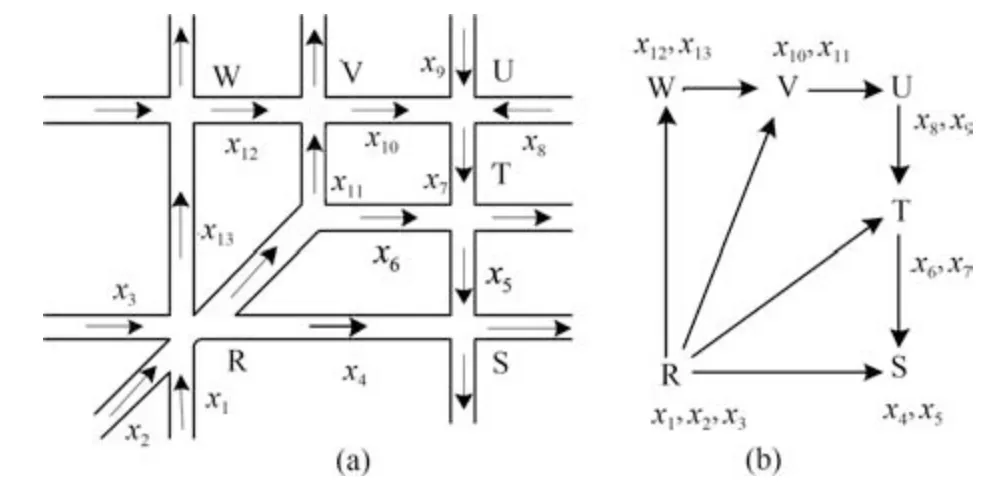
图2 区域分解的例子((a)实验区域;(b)实验区域的分解情况)Fig.2 Example of network decomposition((a)A test network;(b)The decomposition of (a))

由于MPC 具有解决实际交通的不确定性和避免近视控制方案的能力,采用MPC 协调城市区域网络的信号控制也特别有利于本文的研究.因此,优化的存储–转发的方法得出的交通动态模型可以作为预测模型.开发了MPC 信号分割优化框架.就像前文提到的那样,把一个大型区域分割成无数个子区域的目的是减少计算的复杂性.因此,大型区域的优化问题可以转化为各个子区域的相互协作和优化问题.

根据前面提到的子区域划分方法,假定大型区域可以划分成|S|个子区域.定义这些子区域的集合为S,那么子区域Si ∈S的离散时间动态模型为:

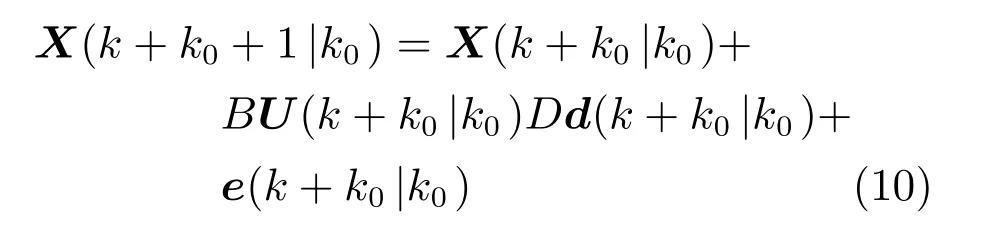
假设当前的时间索引为k0,预测时域为Np.那么子区域Si ∈S的优化问题可以定义为:

其中,X(k+k0|k0)代表在t=k0T时刻对t=(k+k0)T时刻进行预测的状态向量.B和D分别代表控制输入矩阵和需求矩阵.g(·)=C −Li −和h(·)分别代表绿灯时间约束和交通需求约束.Q ≥0 和R ≥0 是两个对角权矩阵.Q是状态(区域中车辆的数)权重.R阵为控制量的权重.

如前文描述,为了减少区域计算的复杂性,本文把区域分解成无数个小的子区域.因此,大型区域的优化问题可以转化成分解子区域的协同和优化.假设利用上述分解原理,可以把大型区域分解成|S|个子区域.定义区域的集合是S,子区域的优化问题可以定义为:

为了简化zj,i(k+k0|k0)可缩写成代表从相邻子区域Sj流入到子区域Si的流入流量.表示从相邻子区域Sj的r交通流流入到子区域Si的交通流量.zj,r;i,l是从相邻子区域Si的r交通流流入到子区域Si的l交通流的预测流量.子区域Si和Sj的相互影响如图3 所示.Ri和Rj分别代表子区域Si和Sj的总交通流数.yi,j(k+k0|k0)表示从子区域Si流出的交通流量.

zj,i(k+k0|k0)和yi,j(k+k0|k0)区-别在于前者表示Sj的预测流入的交通流量,这个交通流来自于Si. 后者表示从Si流出的实际交通流量,这个交通流流入Sj.相对应于zi,j(k+k0|k0),可以定义Mi,j和Mj,i是相互影响的矩阵,它们反映了子区域中交通流的输入流和输出流的关系.可以导出:

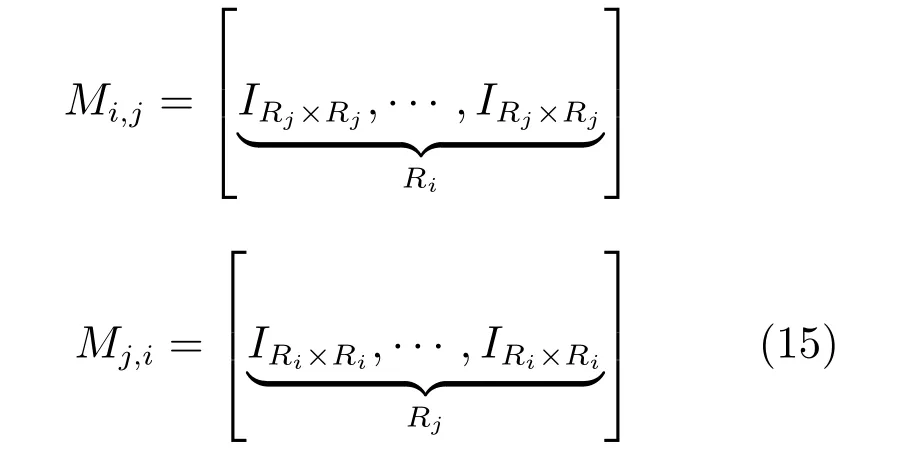
其中,IRj×Rj和IRi×Ri分别是维数Rj和Ri的单位矩阵.

图3 相邻区域之间的影响Fig.3 Influence between adjacent subnetworks

另外,为了更准确地对实际交通情况建立模型,从子区域Si的r1 交通流驶出转入子区域Sj的r2交通流的车辆数量可以通过下式计算:

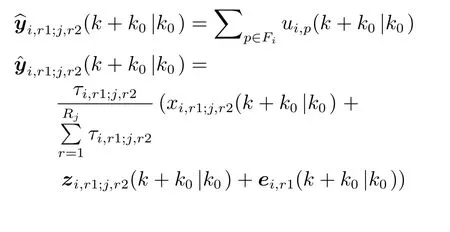
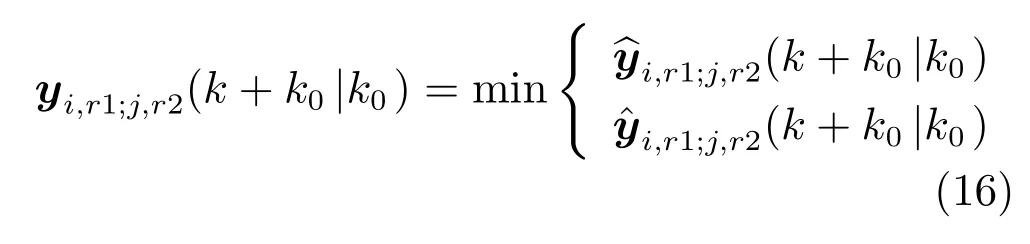
基于上述讨论,可以推导出每个子区域的优化问题.另外需要注意的是,基于预测输入即zj,i的子区域Si的优化问题可以解决.因此,为了反映子区域和它相邻的子区域之间的关系,必须添加下面的相互平衡的约束条件,

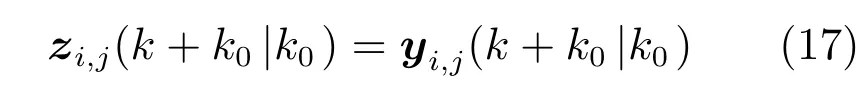
一般来说,为了协调分割后的子区域,整个区域的优化问题(10)可以定义为:

约束条件为式(13)∼(17).

3 分层MPC 控制系统设计

由于大规模系统通过集中控制结构很难得到理想的鲁棒性和可靠性,而且在大规模系统的最优控制计算复杂性大.鉴于这些原因,在大规模系统中可使用分层控制结构,结合分解、协调和并行处理进行改进.分级控制背后的基本原理是通过一些互相联系的变量将给定的大规模系统分解为几个子系统,然后定义每个子系统的优化问题,协调子系统导出一个最优的解决方案.目标协调法和关联预估法可用于协调改进,但目标协调法通常需要额外的术语引入到代价函数,以避免解决方案有奇点,有奇点可能增加计算负担.相比之下,关联预估方法有潜力加快计算过程.因此,在本文研究中将注意力放在关联预估方法上.

如果子区域Si和相邻子区域之间的交互可以通过通信估计,然后为了减少较大的计算量,大规模的城市区域网络可以分解成几个小的子区域,与之相对应的优化问题可以分为几个子区域的优化.因此,为了确保满足子区域Si和相邻子区域之间的互动平衡约束,子区域Si需要和相邻的子区域之间沟通和协调.为了协调所有划分的子区域、需要设计层次(或分布)控制结构下协调算法.

需要注意的是,为了方便起见在接下来的讨论中,时间步长k+k0|k0简写成k,例如z(k+k0|k0)和yi,r1;j,r2(k+k0|k0)分别简写成z(k)和yi,r1;j,r2(k).

3.1 基于MPC 优化目标分析

一般来说,对偶优化方法可以用来解决分解子网之间的协调问题.所有相互约束条件可以考虑采用拉格朗日乘子向量λ.整个交通网络优化问题(13)的增广拉格朗日函数可以被定义为:

其中,λi,j是对应每个子系统的拉格朗日乘子,它与子网Si和Sj之间的约束有关[17].

拉格朗日对偶原理:定义函数θP(X,U)=maxλL(X,U,λ),下标P表示原始问题.假设给定某个U,如果违反原始问题的约束问题,即存在某个使得zj,i(k)=yj,i(k),那么就有

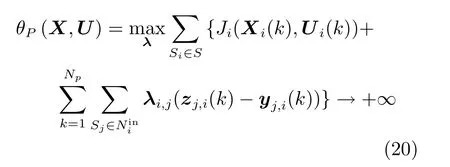
相反的,如果满足约束条件,则由式(17)和式(18)可知:θP(X,U)=J(X,U)

因此:

称为原始问题的值.

定义θD(λ)=minU L(X,U,λ),再考虑极大化D(λ),即P∗=minU θP(X,U)

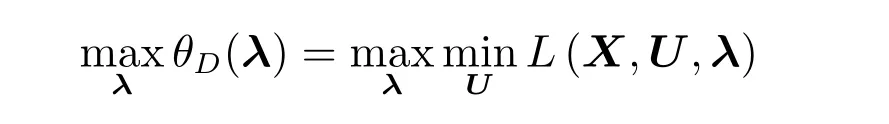
问题maxλminU L(X,U,λ)称为广义拉格朗日函数的极大极小问题.可以将广义拉格朗日函数的极大极小问题表示为约束最优化问题:

称为原始问题的对偶问题.定义对偶问题的最优值

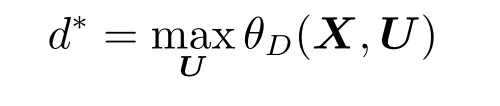
称为对偶问题的值.

定理1.若原始问题与对偶问题都有最优值,则

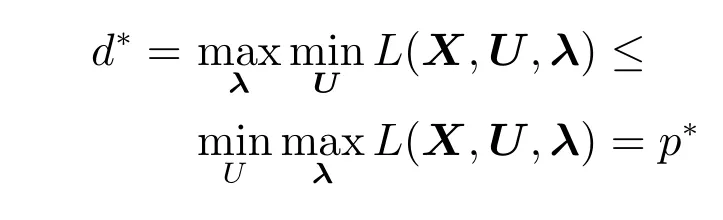
证明.对于任意的λ和(X,U),有

由于原始问题和对偶问题都有最优值,所以

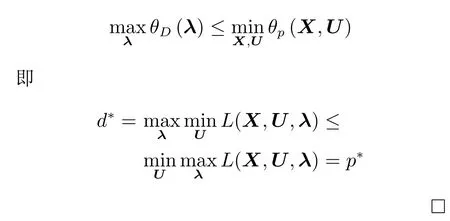
基于拉格朗日对偶原理,拉格朗日对偶函数可以定义为:

约束条件是式(13)∼(17),优化变量U称之为原始变量,拉格朗日算子λ也被称为对偶变量.然后,与问题(19)相关的增广对偶优化问题可以定义为:

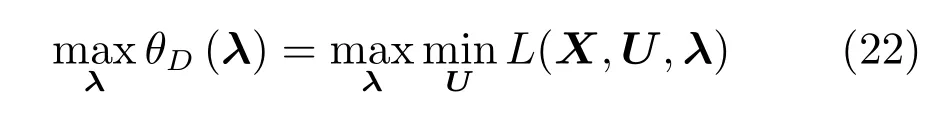
约束条件是(13)∼(17),并且

为了减少计算的复杂性,也为了保证每个子网络都能独立被优化.给出下面这个引理.

引理1.如果拉格朗日乘子λ和作用矢量zj,i(k)固定不变,拉格朗日函数可以被扩展成:

然后将(24)代入到对偶优化问题(22)中,可以得到:

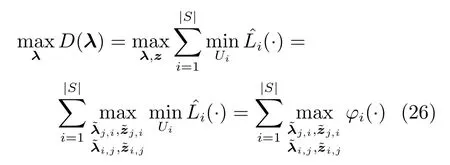
约束条件为式(11)∼(16)和式(24).

3.2 分层MPC 控制器设计

基于以上讨论:可以采用两层模型预测控制解决对偶优化问题.在上层控制中优化协调量λ,z,在下层控制中通过求解每一个子区域的优化问题φi(·),求得下层控制的优化目标U.

下层控制:在下层控制中,每一个子区域的优化问题是:

约束于式(13)∼(17).值得注意的是,在解决子优化问题(26)过程中,拉格朗日乘子以及作用矢量在解决子区域的优化过程中被认为是常量.

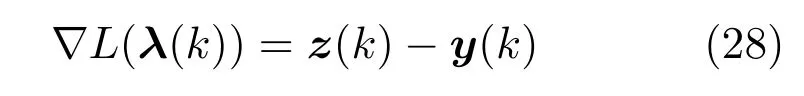
为了方便说明,定义:

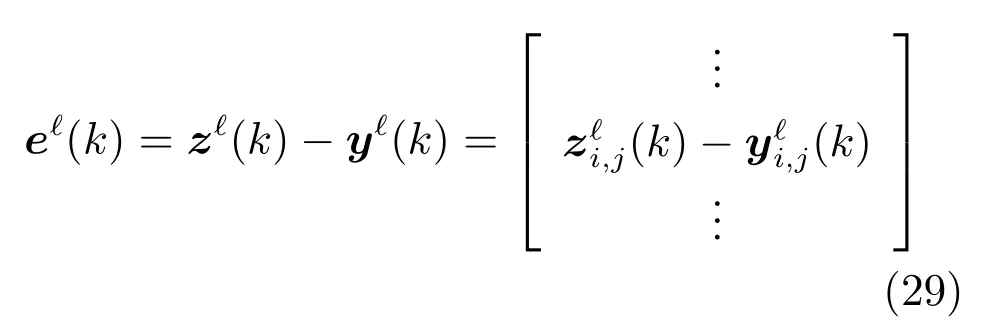
然后,对于任意的子区域Si和它的相邻子区域Sj,拉格朗日算子λi,r1;j,r2和λj,r3;i,r4可以更新如下:

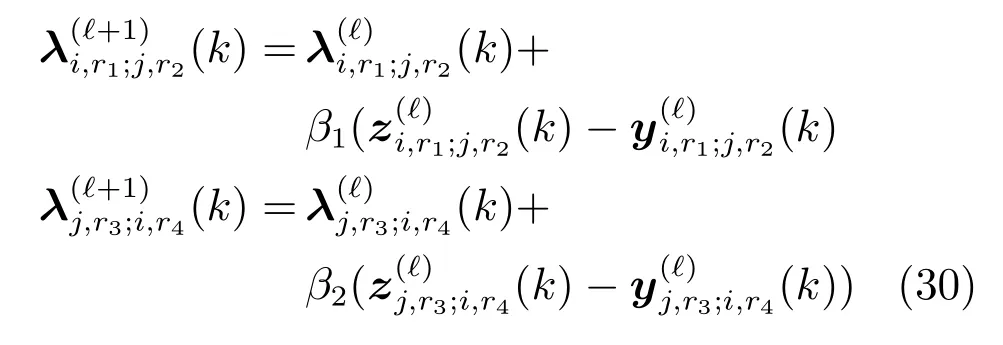
其中,β1和β2是正定的常量,表示给定的步长,可以是所有迭代的固定值,或者可以针对每次迭代变化和优化.上标表示迭代步骤.

基于交互预测方法的理论基础,任意两个子网络Si和Sj之间的作用矢量zi,j和zj,i通过上层协调量估算.作用矢量在下层控制的各个子区域的MPC 优化量中收集信息.因此,在(+1)步迭代中,作用矢量的估计量可以更新如下:

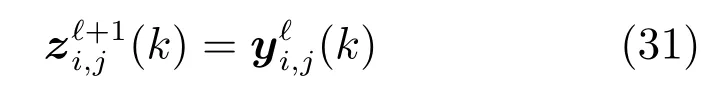
将式(29)代入式(27),可得:

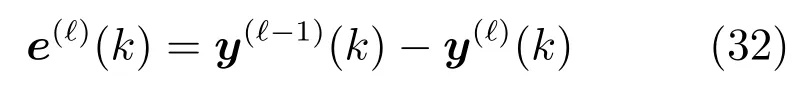
然后结束协同的条件可以定义为:

其中,0<ε是给定误差容限阈值.

另外,在式(28)和式(29)中值得注意的是,迭代过程是从开始的.因此,任意的子区域Si和它的相邻子区域Sj,拉格朗日算子和以及作用矢zi,j和zj,i都必须在第一步迭代中初始化.

图4 说明了所提出的方法的方案图.

3.3 区域交通信号控制算法

算法1(区域交通信号控制算法).

步骤1 (初始化).假设在当前采样步长k0的所有初始状态Xi(k0)(i=1,2,···,|S|)均是可测的,对于k=k0+1,···,k0+Np,关联向量都能被初始化.令c=1.

步骤2 (预测).对于k=k0+c −1,···,k0+c −2+Np,假设可以预测子区域Si的交通流r的交通需求di(k)和扰动ei(k).令-=1.如果c=1,则跳转到步骤4.

图4 所提出方法的方案图Fig.4 Scheme of the proposed method

步骤3 (启动).对于任意的i=1,2,···,|S|和k=k0+c −1,···,k0+c −2+Np,

步骤4 (下层优化).对于任意的i=1,2,···,|S|和k=k0+c −1,···,k0+c −2+Np,由于关联向量量可以由上层控制得到,每个子区域Si的MPC 优化量记忆可以通过解决式(27)中的最优化问题得到决策向量同时,可以通过(16)计算得到输出交通流量,然后将这组数据传送到上层优化控制.

步骤 5 (上层优化).对于任意的i=1,2,···,|S|和k=k0+c −1,···,k0+c −2+Np,基于迭代预测的方法,应用下层优化得到的根据式(30)和式(31)更新

步骤6 (检验和更新).检测是否满足最终的迭代条件,如果在迭代次数时满足停止条件,然后结束迭代过程,跳转至步骤7;否则,返回到步骤4.

步骤7 (完成).对于任意的交叉路口i=1,2,···,|S|,最优控制变量序列应用到子区域Si.

步骤8 (滚动时域).将时域移动到下一个控制间隔,令c=c+1,跳转至步骤2.

4 仿真结果及分析

为了验证本文改进模型后分层协调模型预测控制算法的有效性,本节主要通过与文献[15]中所提出的存储–转发模型进行对比,从计算成本和算法性能两个方面对比分析,评估本文算法的优越性.对于计算成本的度量,本文采用了在不同的预测范围Np内,用于解决在线优化问题的模拟的平均CPU运行时间.对于算法性能的度量,采用在测试网络中1 小时(即30 个模拟步骤)的测试中车辆的总时间消耗(TTS).

研究对象主要是图2 所示的交通网络,测试网络中包括18 条交通流,其中有5 条是流出的交通流,其余13 条是流入的交通流.因此x1,x2,x3和x8,x9是所研究网络的流入交通流.x3和x4的长度是一样的,都是1 200 m,x6和x11是1 440 m,其他长度都是600 m.此外,为了保证同步,假定任意两个交叉口之间的偏移量都是零.表1 给出了基本参数的定义,表2 给出了测试路网中各个交通流的转弯率,不存在直接转弯关系的交通流转弯率为零.

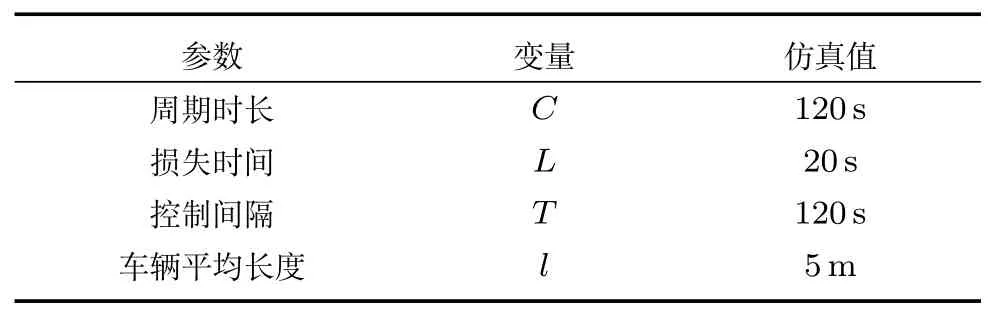
表1 基本参数的定义Table 1 Definitions of basic parameters

图5 给出了5 条输入交通流在仿真时间段的随机变化情况,变化周期是10 min (相当于5 个仿真步数).图5 测试网中的每条流入的交通流的变化周期是10 min (相当于5 个仿真步数),初始状态和扰动是随机产生的,为了简化,初始状态和扰动的定义如表3 所示.

图6 说明了在预测时间窗不同的情况下,每个仿真周期中基于两种不同模型的CPU 运行时间.

表2(a) 测试网中的转弯率Table 2(a) Turning rates of the test network

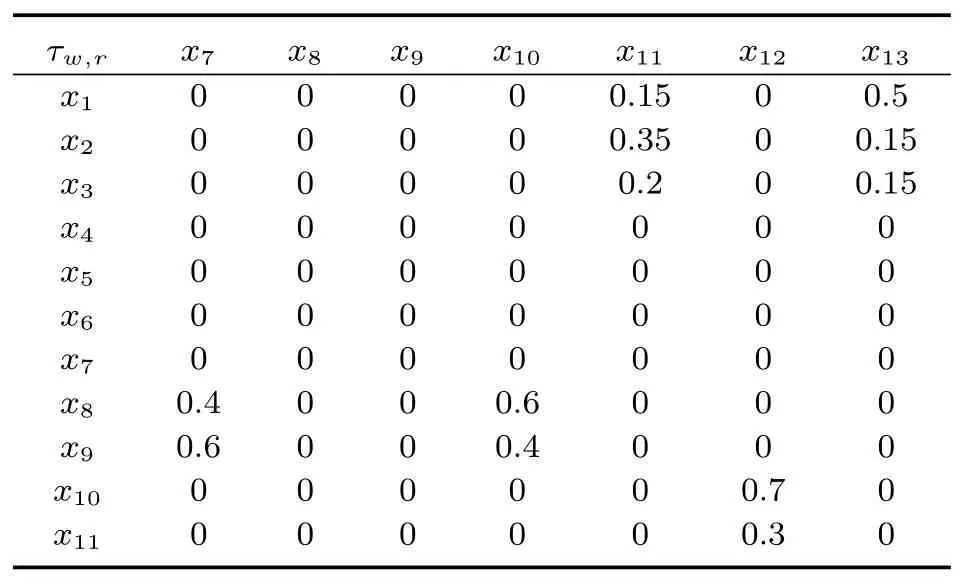
表2(b) 测试网中的转弯率Table 2(b) Turning rates of the test network

表3 初始状态和扰动Table 3 initial states and disturbances

从表中可以看出,随着Np的增长,基于两种模型的CPU 运行时间都在迅速的增加.同时,与文献[15]中的存储–转发模型相比,因为改进模型对流量的高效疏散,本文改进的存储–转发模型的每个仿真的CPU 运行时间会减少0.25%∼70.25%.另外,从表中可以看出,随着Np的增长,本文改进模型控制策略的性能优势更为明显.

图7∼10 表明了不同预测窗下,对应测试的6 种不同状态(低初态低扰动LSLD、低初态高扰动LSHD、中初态低扰动MSLD、中初态高扰动MSHD、高初态低扰动HSLD、高初态高扰动HSHD)下,测试区域中车辆总的消耗时间(TTS)的情况.

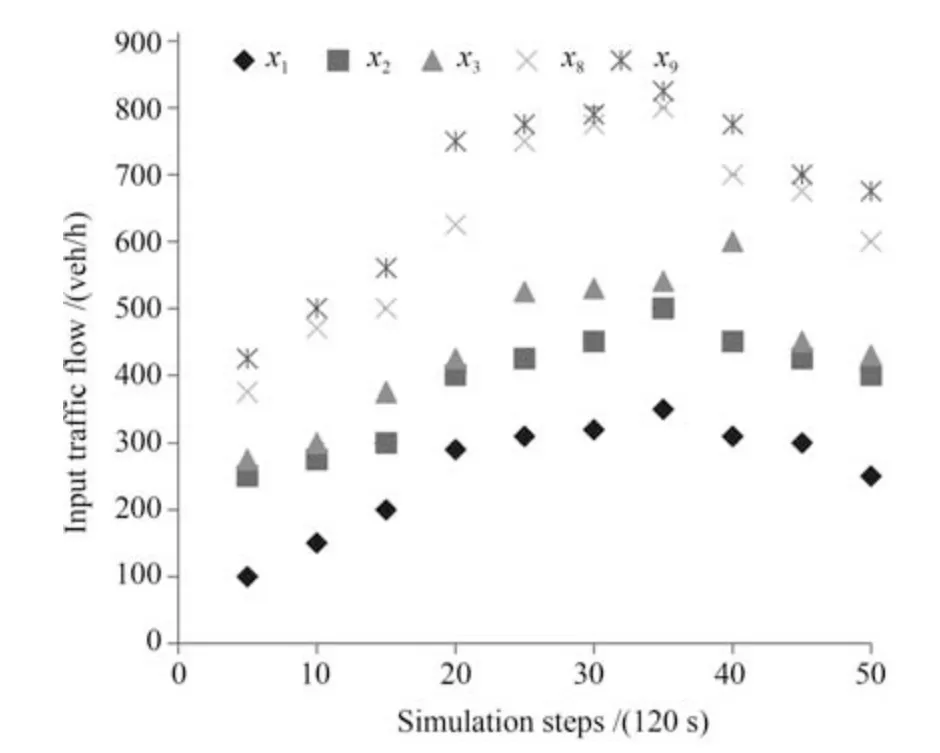
图5 外界输入交通流Fig.5 Input traffic flow from outside

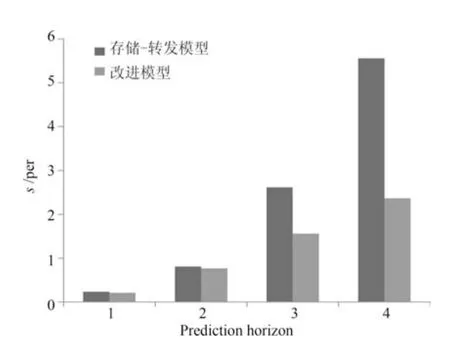
图6 不同预测窗的运行时间Fig.6 Running time under different prediction window

图7 Np=1 时不同状态下两种模型的TTSFig.7 TTS of each model under Np=1

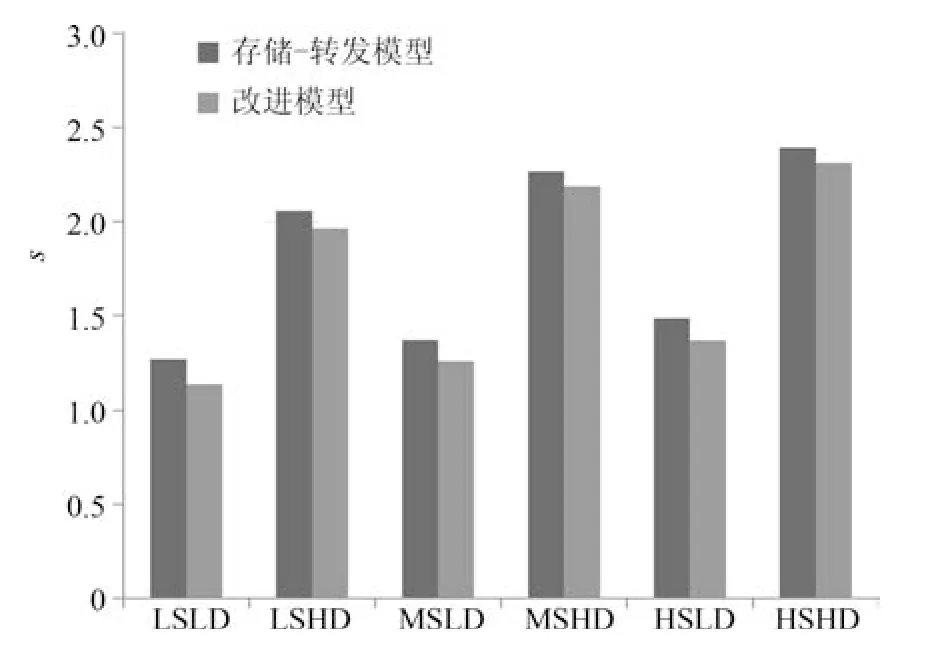
图8 Np=2 时不同状态下两种方法的TTSFig.8 TTS of each model under Np=2

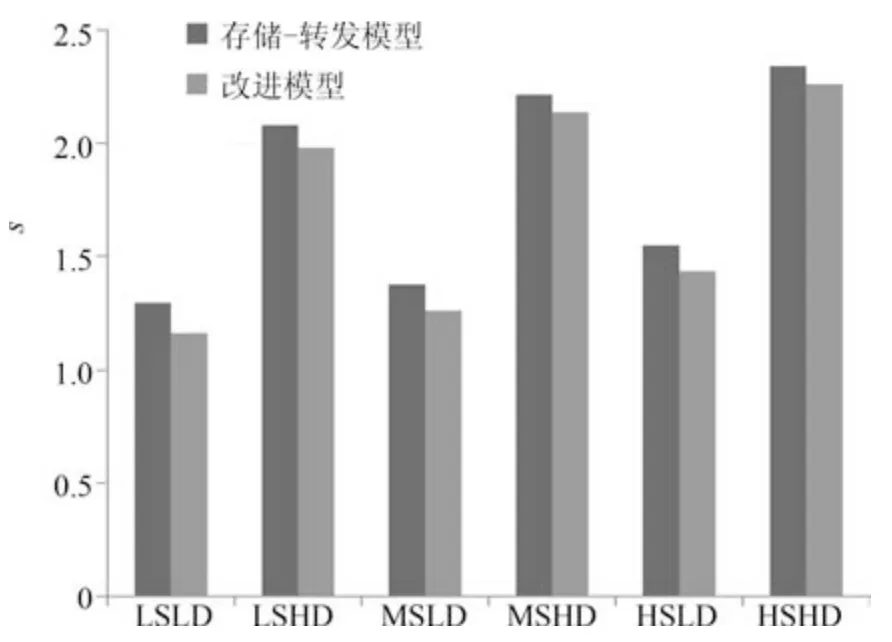
图9 Np=3 时不同状态下两种方法的TTSFig.9 TTS of each model under Np=3

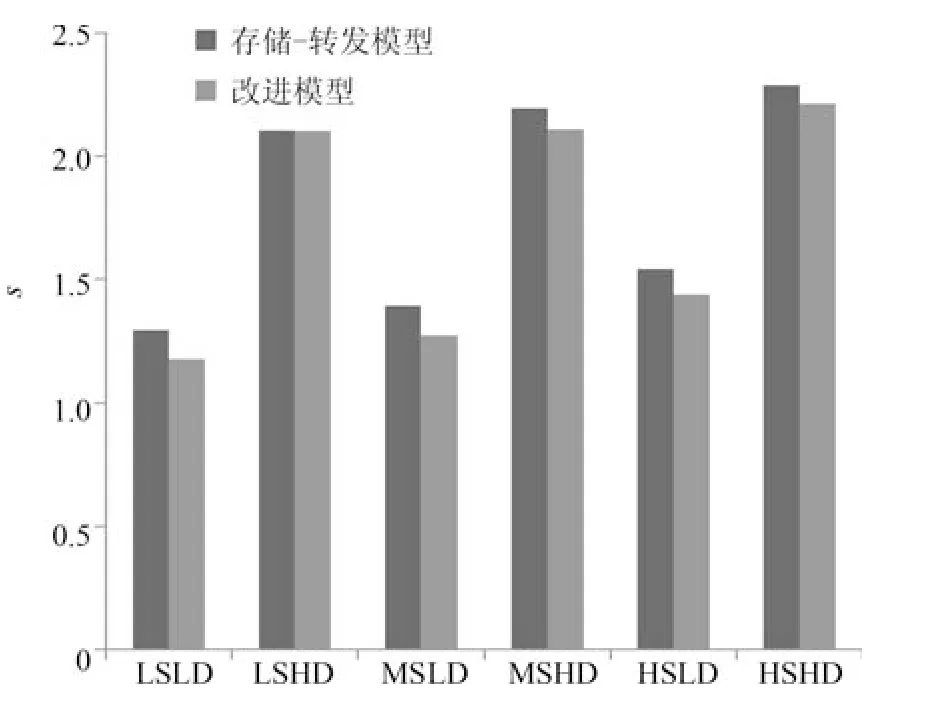
图10 Np=4 时不同状态下两种方法的TTSFig.10 TTS of each model under Np=4

从上述4 图中,可以看出在不同状态下,分布式模型预测控制的TTS 都短于集中式模型预测,并且随着预测窗的增大,TTS 呈增长的趋势.

下面从不同类型交通流的车辆消耗情况来探究本文所述方法的有效性.选取两个具有代表性的交通流进行研究,分别是有外界输入的交通流x3,无外界输入的x7.图11∼14 给出所研究的两个交通流在不同状态下,由两种控制策略分别控制的车辆数量的对比.

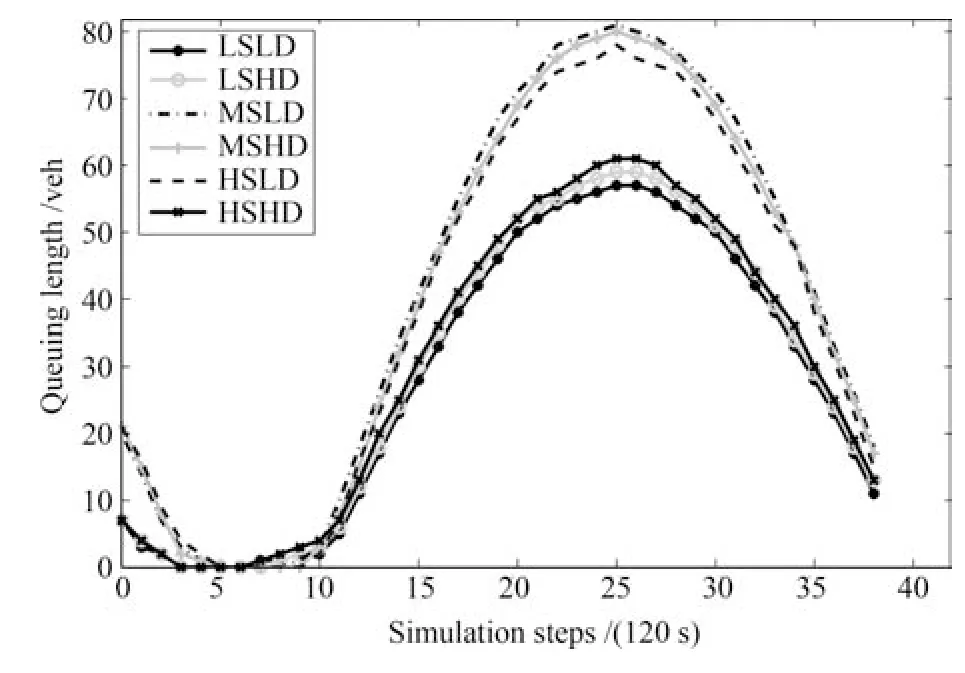
图11 本文改进模型控制的交通流x3的变化Fig.11 The changing of traffic x3under proposed model

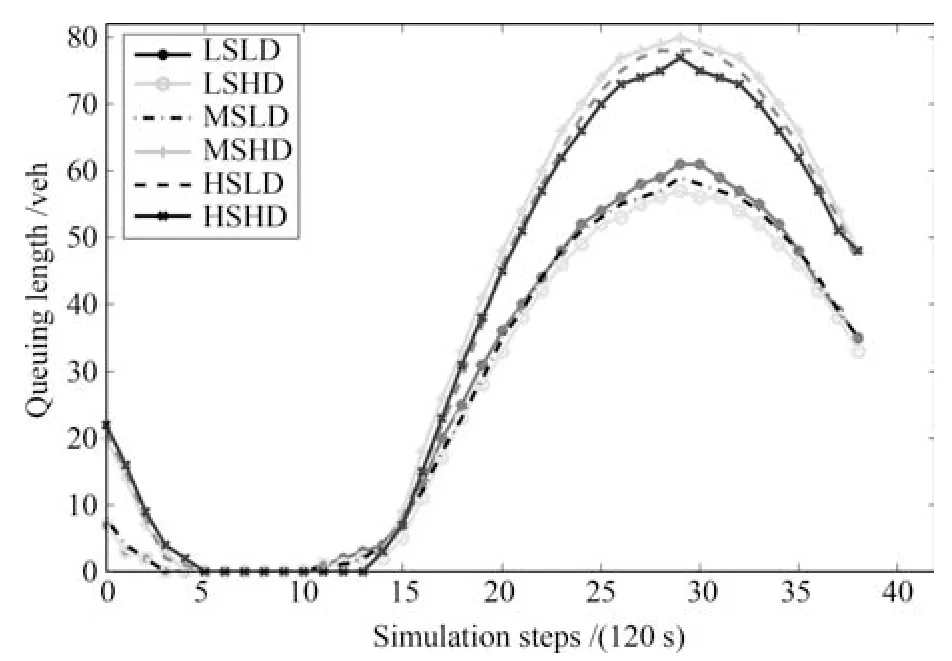
图12 存储转发模型控制的交通流x3的变化Fig.12 The changing of traffic x3under store and forward model

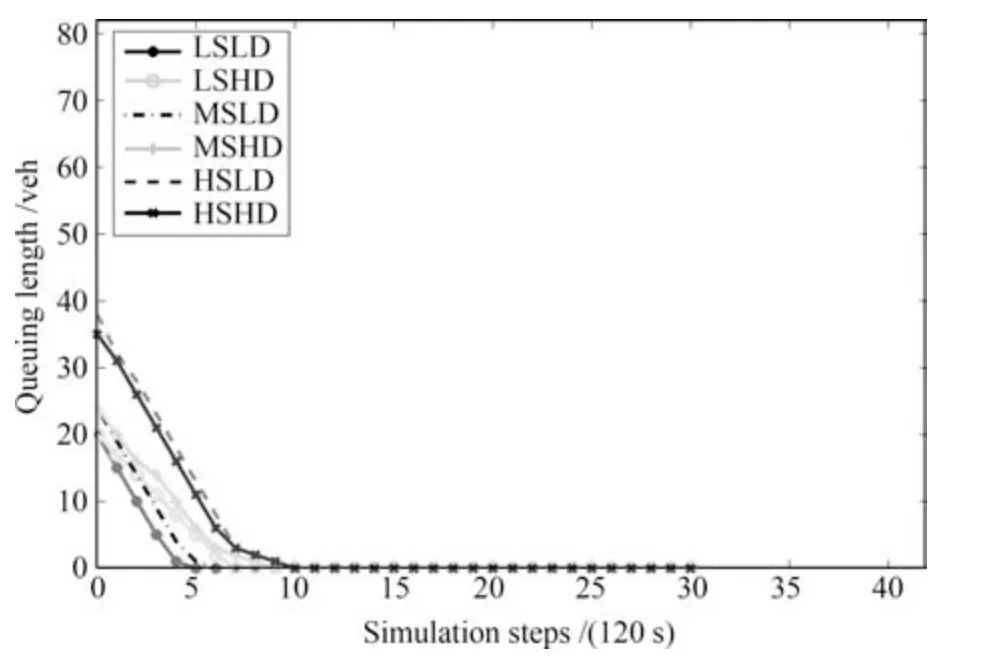
图13 本文改进模型控制的交通流x7的变化Fig.13 The changing of traffic x7under proposed model

观察上述4 图,首先在相同状态下,由两种不同模型控制的交通流,车辆排队数量的变化趋势几乎是一样的.由图11 和图12 对比可以发现,不管初始排队车辆处于什么状态,低扰动下交通流x3的车辆排队数量远远低于高扰动状态下的车辆排队数量.由图13 和图14 对比可以发现,相同状态不同控制策略下对交通流x7的控制性能几乎相同.

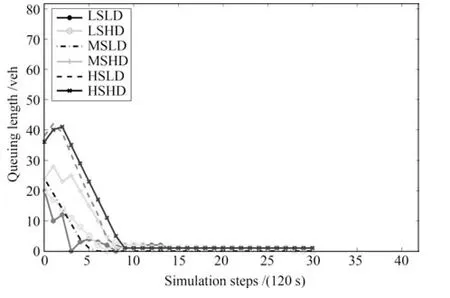
图14 存储转发模型控制的交通流x7的变化Fig.14 The changing of traffic x7under store and forward model

对比图11 和图12 可见,图11 中,约10 个仿真步数(即20 min)后,排队数量出现了递增的趋势,并且出现了最大值.这是因为x3是有外界输入的交通流,所以排队长度的车辆数量远远大于没有外界流入的交通流排队数量.图11 的队列长度峰值比图12 提前出现,但到仿真结束时,平均队列长度下降到了图12 的1/3 左右.

综上所述,本文提出改进的存储–转发模型在计算损耗和总的损失时间(TTS)上,性能优于文献[15]的存储–转发模型,尤其是随着预测时间窗长度的增加,优势越来越明显.同时,相同条件下,两种控制模型对排队车辆的消耗情况是一样甚至更优的.也就是说,在能达到相同的控制性能情况下,本文提出的改进的存储–转发模型在整个运行的计算速度上更优,这也是大型控制系统追求的目标.

5 结论

本文主要是针对区域交通进行研究,根据交通流的动态特性,提出了改进的存储–转发模型,建立相应的区域交通状态方程.为了减小计算复杂度,本文根据相应的子区域划分原则,把大型区域划分成小的子区域.根据模型预测控制理论,提出区域交通的优化问题,给出相应的约束条件.为了协调各子区域,引进了分布式模型预测控制算法.仿真结果表明,在能达到相同的控制性能情况下,本文提出的基于改进的存储–转发模型的算法在解决问题的计算速度上优于文献[15]中基于存储–转发模型的分层模型预测.