变参考轨迹下的鲁棒迭代学习模型预测控制

马乐乐 刘向杰

现代过程工业中存在着一类间歇过程[1],如半导体加工、制药、注塑、发酵等.间歇过程通常具有重复特性,且对跟踪精度要求较高,是典型的非连续操作.其控制任务是在每个生产批次内跟踪给定的参考轨迹[2].迭代学习控制(Iterative learning control,ILC)能够利用过去批次的信息进行优化学习,不断调整控制输入轨迹,逐步提高跟踪性能,实现对参考轨迹的高精度跟踪,因此被广泛应用于间歇过程控制中[3].但是由于ILC 是典型的开环控制,因此不能保证控制系统的时域稳定性,难以处理实时干扰.模型预测控制(Model predictive control,MPC)作为先进过程控制技术[4],不仅广泛应用于工业过程的优化控制[5−6],同时也成功应用于轨迹跟踪控制[7].它通过预测未来的系统状态及输出,进行滚动时域优化,能及时处理实时干扰,保证时域跟踪性能及闭环系统稳定性,弥补ILC 的不足.迭代学习模型预测控制(Model predictive iterative learning control,MPILC)结合了MPC 与ILC 的优点,因此成为控制间歇过程的有效方法.

早期的MPILC 算法大多基于输入输出模型,如受控自回归积分滑动平均(CARIMA)模型[8−9],脉冲响应模型[10].而近年来基于状态空间模型的MPILC 算法研究受到了更多关注,研究对象包括线性定常状态空间模型[11]、带干扰项的状态空间模型[12]以及含不确定性的状态空间模型[13].其控制器设计通常需要进行状态增广以构造二维误差模型.为加强控制器鲁棒性,很多学者在此基础上提出控制器结构改进算法,如构造分段优化[14],改善学习机制[15].

典型的间歇过程通常具有强非线性,而现有的MPILC 算法大都是针对线性系统构造的.文献[14−15]将原非线性系统在工作点简单线性化,文献[10]沿参考轨迹进行线性化.由线性化带来的模型失配问题会在一定程度上影响时域跟踪性能以及迭代学习速度,这在实际生产上将造成原料浪费以及经济效率下降.近年来许多学者在MPILC 研究中通过各种建模手段来近似非线性系统,包括T-S 模糊建模[16]、神经网络建模[17]、数据驱动建模[18]等.但是这些方法需要大量过程数据的支持,以及极其复杂的调参、学习过程才能建立较为精确的模型.

线性参变(Linear parameter varying,LPV)蕴含技术是处理复杂非线性的有效手段,已被广泛应用于非线性模型预测中[19].原非线性系统在工作区间的动态特性可以包含在由LPV 系统构成的多胞里.因此,只要保证基于LPV 模型的控制系统的稳定,就能够保证非线性控制系统的稳定[20].由于LPV 模型中存在的参数不确定性,其控制求解一般通过线性矩阵不等式(Linear matrix inequality,LMI)约束下的目标函数优化来实现.

间歇过程的参考轨迹会由于不同的产品规格、生产效率以及外在干扰而发生改变.比如半导体制造中的蚀刻系统必须跟踪不同的操作轨迹来生产不同规格的晶片[21].而一旦参考轨迹发生变化,经典迭代预测控制需要重新进行初始化,并经历多个批次的学习来跟踪新轨迹[10],适应能力较差.近年来许多学者提出改进的自适应ILC 算法来解决变参考轨迹跟踪控制问题.文献[21]针对随机系统变轨迹跟踪问题,提出两种自适应ILC 策略,一是在控制器设计中选择当前批次的输出轨迹与下一批次的参考轨迹的差值作为新的状态变量,另一种是在每一个批次的末尾利用卡尔曼滤波器重新进行系统辨识;文献[22]针对离散非线性系统,设计模糊自适应ILC 控制器,通过不断更新模糊参数来近似变参考轨迹下的系统动态;文献[23]设计基于数据驱动的自适应ILC 控制器,引入未来批次的参考轨迹作为反馈,并将过去批次的参考轨迹作为前馈以实现对变参考轨迹的跟踪.这些基于ILC 的控制策略通常要求已知所有采样时刻上的参考轨迹变化量,并且由于算法内缺少预测环节导致了跟踪性能和学习效率的下降.针对该问题,可将参考轨迹变化量视为迭代域中存在的有界扰动,构造限制参考轨迹变化量对系统控制性能影响的H∞约束.这样只要在每个采样时刻的优化中满足此H∞约束,就可有效抑制变参考轨迹带来的跟踪误差波动,且只需已知下一采样时刻的参考轨迹变化量.H∞控制[24]可与MPILC 算法有效结合,利用预测控制的滚动时域优化提高时域跟踪性能,从而加快学习速度.

本文提出一种基于LPV 模型的鲁棒迭代学习模型预测控制(Robust model predictive iterative learning control,RMPILC)算法,实现间歇过程对变参考轨迹的跟踪.采用LPV 模型描述非线性系统动态特性,并通过状态增广建立二维误差模型.为保证变参考轨迹下的跟踪性能,引入H∞约束条件.将变轨迹跟踪问题转化为LMI 约束下的凸优化问题.通过针对数值例子以及CSTR 系统的仿真验证了所提出算法的有效性.

1 模型推导

1.1 非线性系统的LPV 蕴含

假设非线性间歇系统由下式表示:

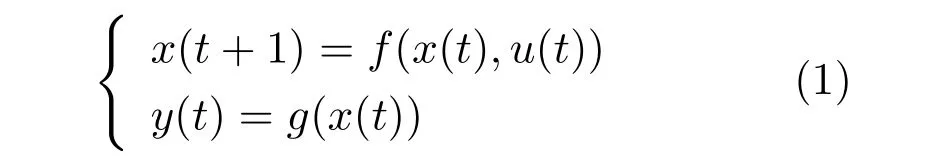
其中,x ∈Rnx是状态变量,u ∈Rnu是控制输入,y ∈Rny为输出变量.t ∈(0,N],N为批次长度.

假设对任意x(t)、u(t)(t ∈(0,N])存在矩阵

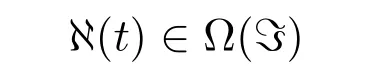
满足

那么,非线性系统(1)的动态特性可由LPV 系统描述:

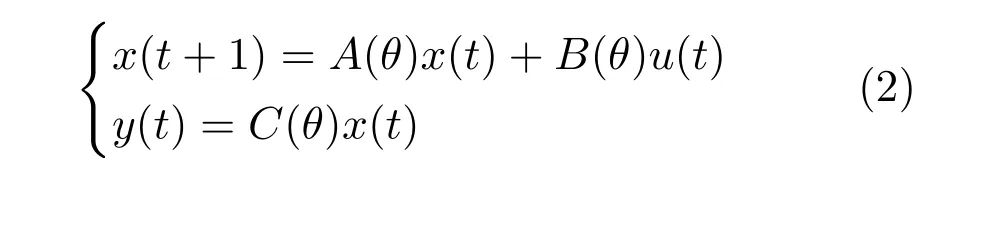
即任何关于LPV 系统(2)的性质适用于非线性系统(1).

间歇过程的LPV 建模问题已经得到了广泛关注[25].其中,选择合适的参数至关重要.对于简单非线性系统,可以通过直接计算非线性项的上下界确定.若被控系统的非线性比较复杂,可以基于系统平衡点,采用数学变换的方法获得合适的表达式[26].

1.2 增广迭代误差模型

建立相邻迭代次序之间的动态关系,得到

定义输出参考轨迹为,那么跟踪误差可以定义为

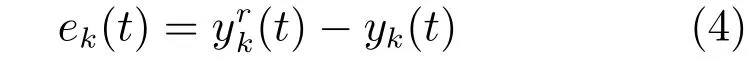
将式(4)代入式(3),得到沿迭代轴的增广迭代误差状态空间模型:

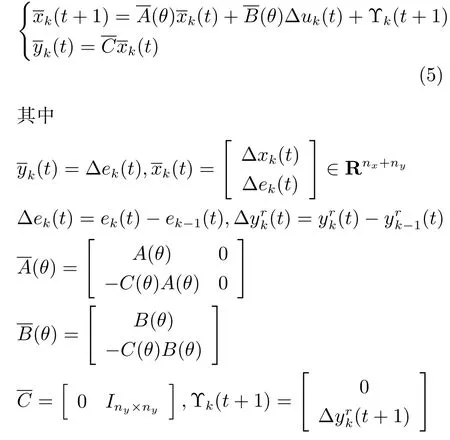
1.3 二维增广误差模型

迭代次序跟踪误差的变化量∆ek(t).则在第k次迭代中,为了将跟踪误差ek(t)控制到0,的参考轨迹应为

由第1.2 节可知,系统(5)的输出为相邻

定义:

联立式(5)和式(6),得到同时包含迭代域和时域动态特性的二维增广误差模型

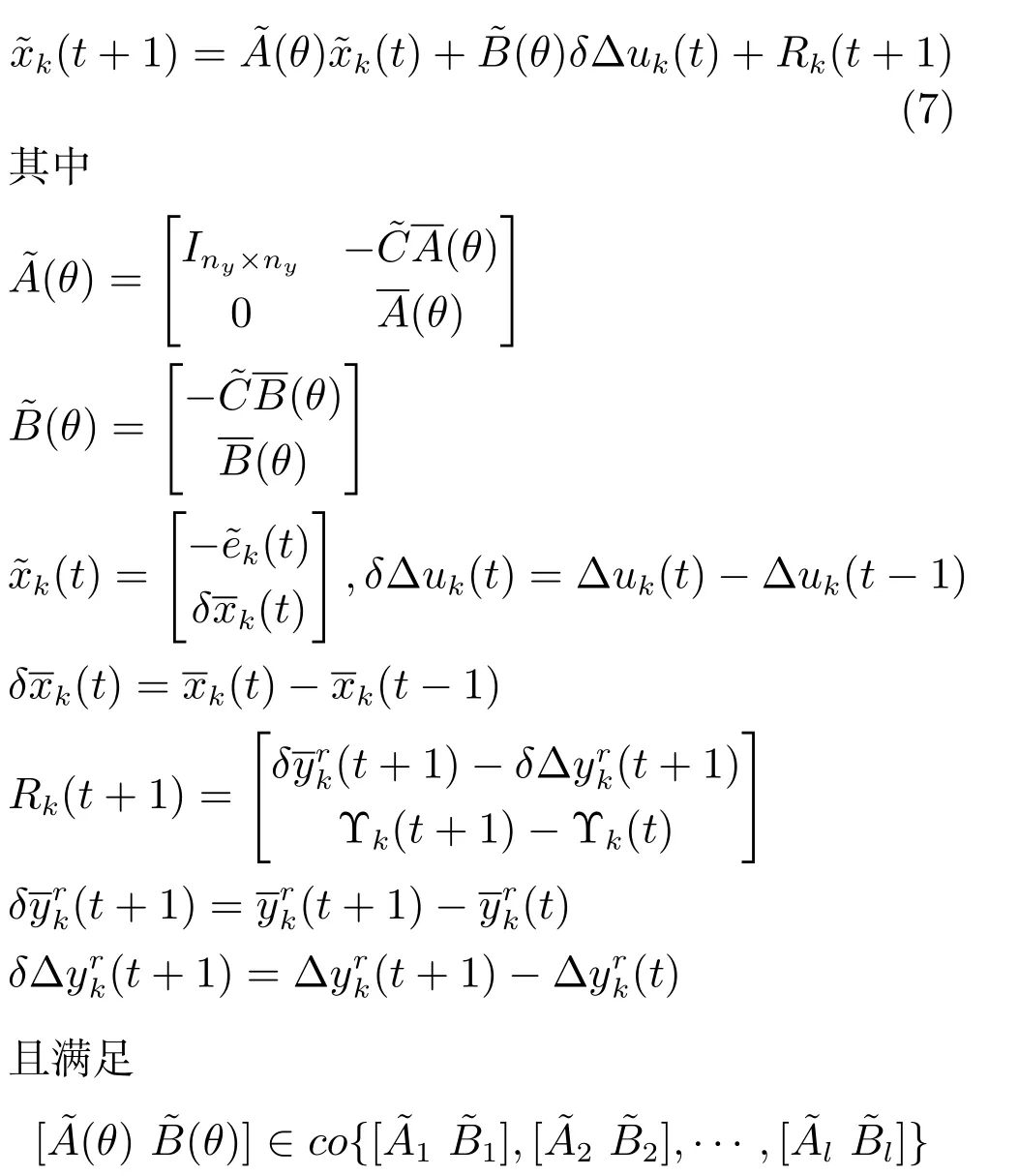
注1.Rk(t+1)包含了参考轨迹变化量,为已知有界时变量,与状态变量、控制输入变量均无关,可以看作迭代域上的有界外部干扰.

注2.模型(7)与典型的二维Rosser 模型[27]不同,它将在同一个状态方程中建立时域与迭代域上动态关系,其中都是同时包含时域及迭代域信息的二维变量.

因此,系统(1)的轨迹跟踪问题可以转化为系统(7)的零点跟踪问题.其控制任务包括:

2)限制参考轨迹变化量Rk(t+1)对控制性能的影响;

3)防止控制输入波动过大.

2 RMPILC 算法

2.1 问题描述

根据控制任务1)和3),结合鲁棒H∞控制,定义控制性能指标zk(t)∈Rnx+2ny+nu

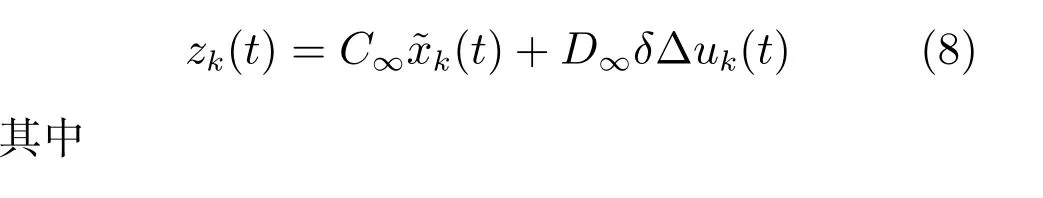
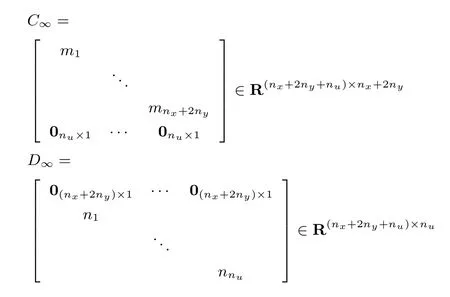
mi(i=1,2,···,nx+2ny),nj(j=1,2,···,nu)为可调权重系数.显然,目标函数可表述为zk(t)的二次型:

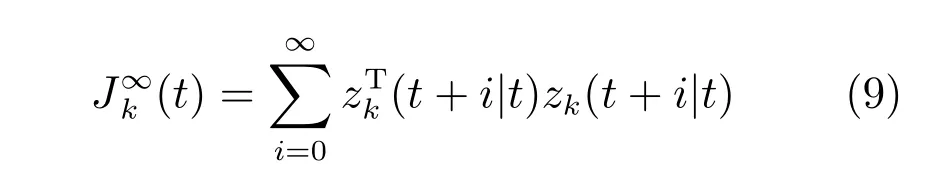
为实现控制任务2),引入H∞范数

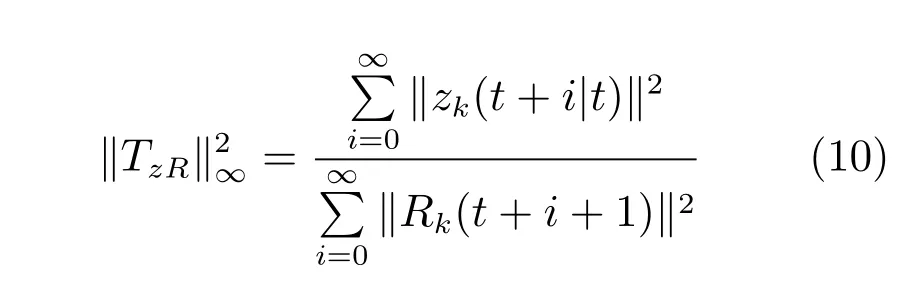
设置H∞性能指标

其中,ε>0 为给定的H∞性能上界.不等式(11)表示参考轨迹变化量Rk(t+1)对跟踪性能指标zk(t)的影响被限制在由ε定义的范围内.

因此,满足以上三项控制任务的优化问题可以描述为:

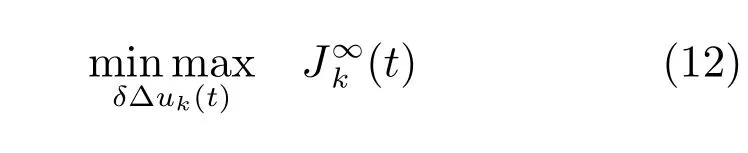
满足式(8)和式(12).

2.2 鲁棒稳定状态反馈控制律

定义状态反馈控制律

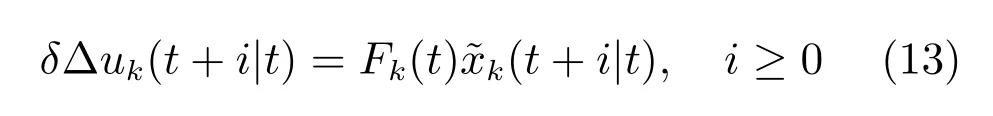
为表达简洁,推导过程的书写省略θ.考虑二次型函数可得

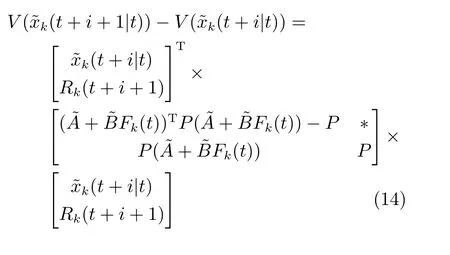
将式(14)从i=0 累加至i=∞,可得

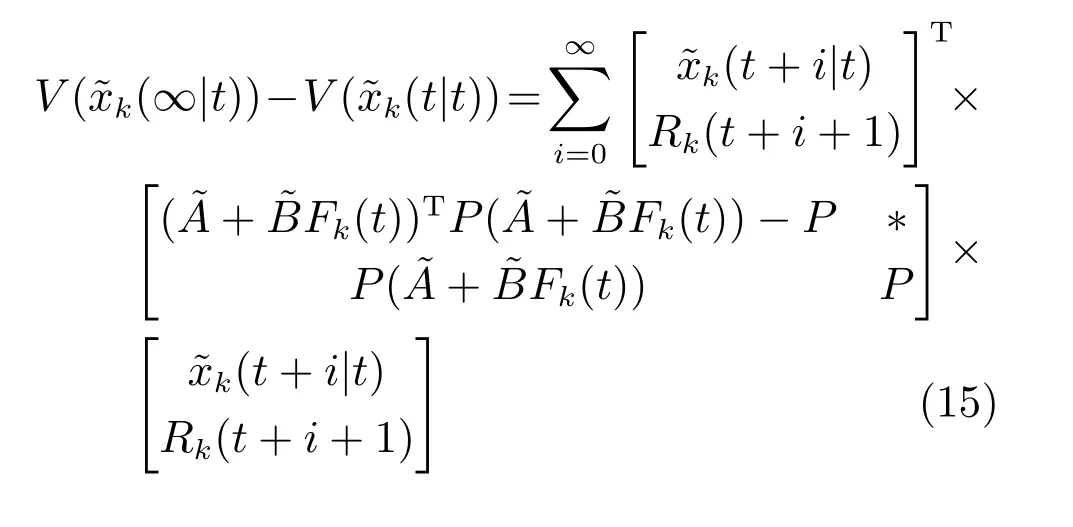
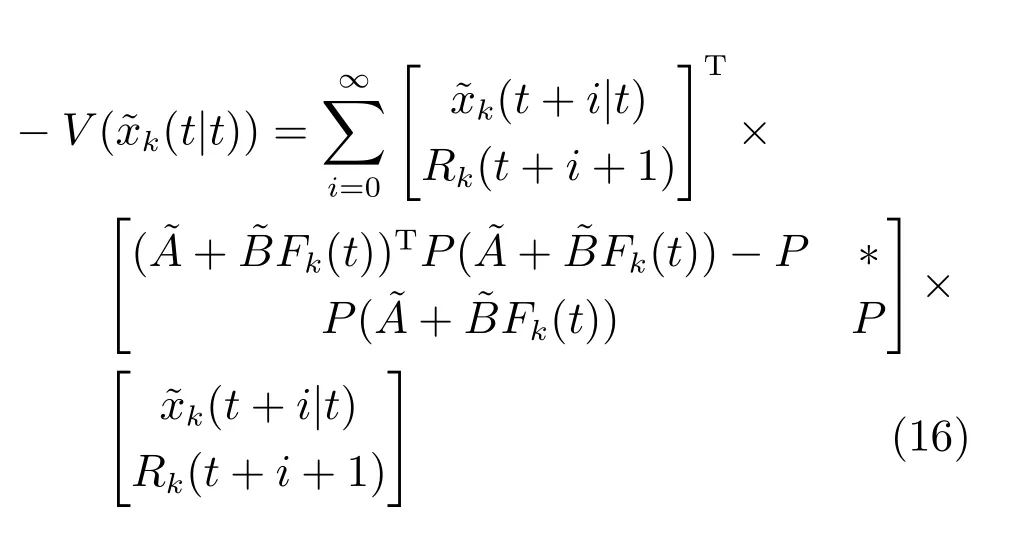
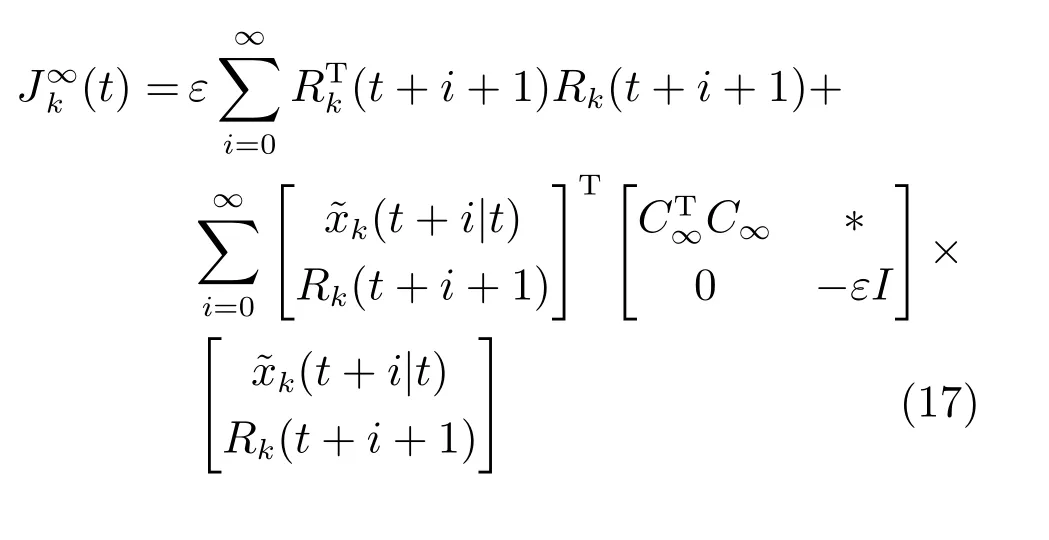
联立式(16)和(17),目标函数(9)有以下形式

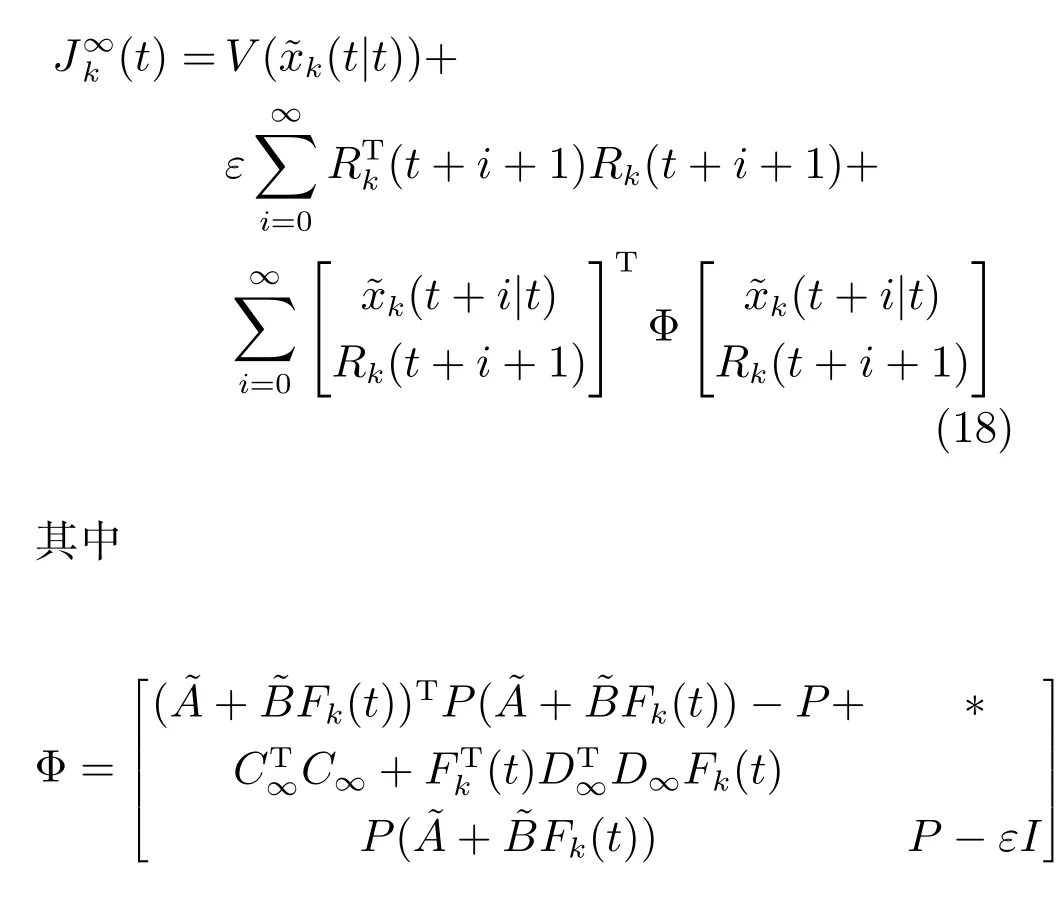
引理1.当且仅当Φ<0,能够满足H∞性能指标(11).

证明.在式(14)两端同时加上可得

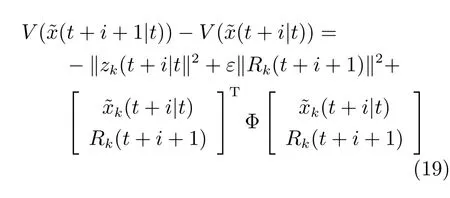
若Φ<0,则有

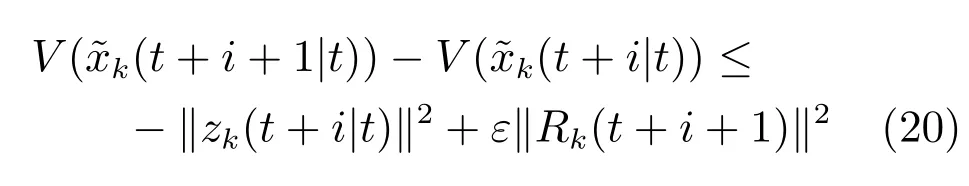
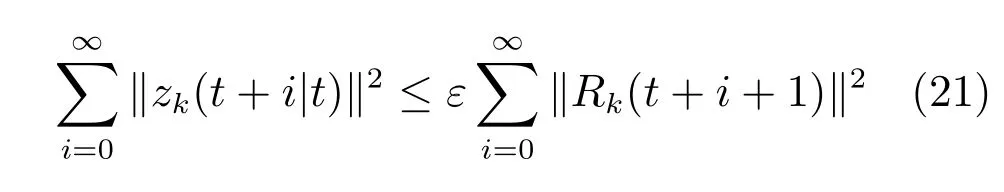
式(22)与H∞约束(12)等价.

在Φ<0 的条件下,可以得到目标函数的上界

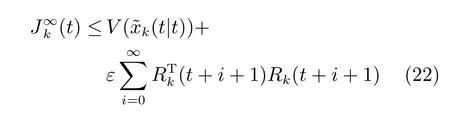
根据式 (7)中Rk(t+1)的定义可知,为有界值.设

联立式(22)和(23),得

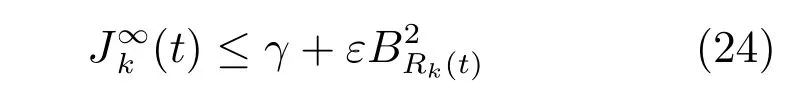
满足

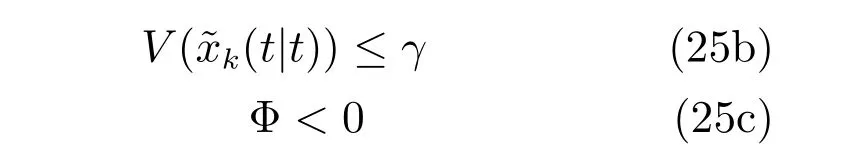
引理2.若优化问题(25)在当前时刻可行,当满足不等式

时,由RMPILC 算法控制的闭环系统是鲁棒稳定的.

证明.联立式(14)及条件(26),可得

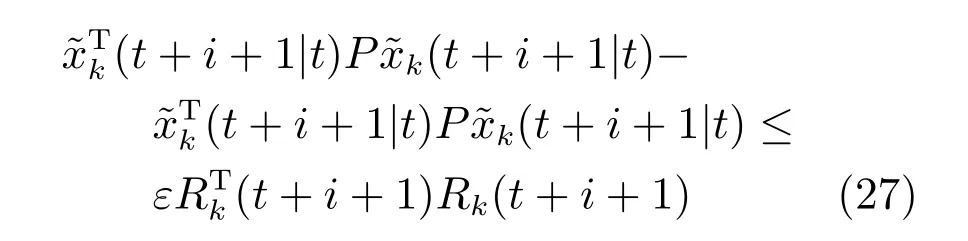
将式(28)从i=0 到i=p −1(p ∈[1,∞))进行累加,可得

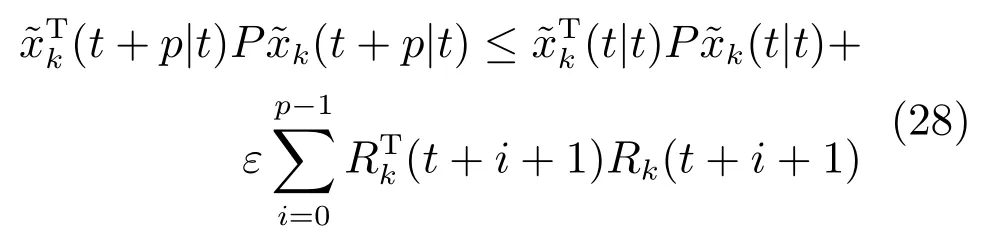
联立式(23)、(26)和(28),可以推出

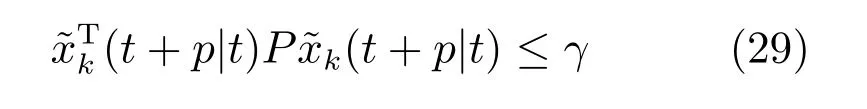
因此,对于任意未来时刻t+p,其状态属于不变集Ω˜xk:

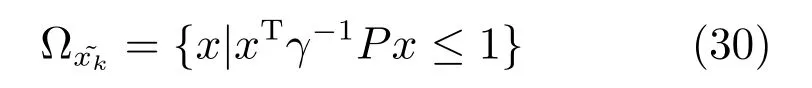
注3.若参考输出保持不变,即Rk(t+1)=0,那么RMPILC 控制下的闭环系统是Lyapunov 意义下稳定的.

证明.根据式(27),若Rk(t+1)=0,能推出

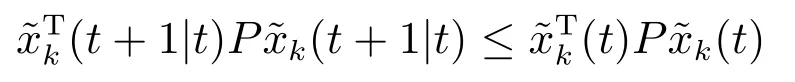
2.3 LMI 求解

为获得满足在鲁棒稳定条件(26)下优化问题(25)的最优解,将其转化为线性矩阵不等式的形式.

引理3.满足约束(25b)、(25c)及鲁棒稳定条件(26)的状态反馈矩阵Fk(t)可通过Fk(t)=Y Q−1计算得到,其中Q=γP−1,Y为下述LMI约束下优化问题的解:

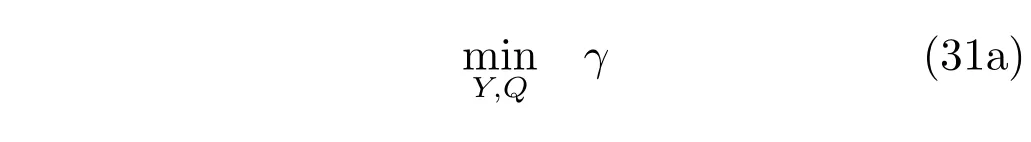
对所有q=1,2,···,l,满足

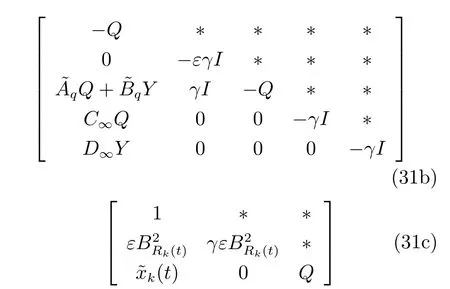
证明.采用Schur 补定理[28],式(25c)等价于

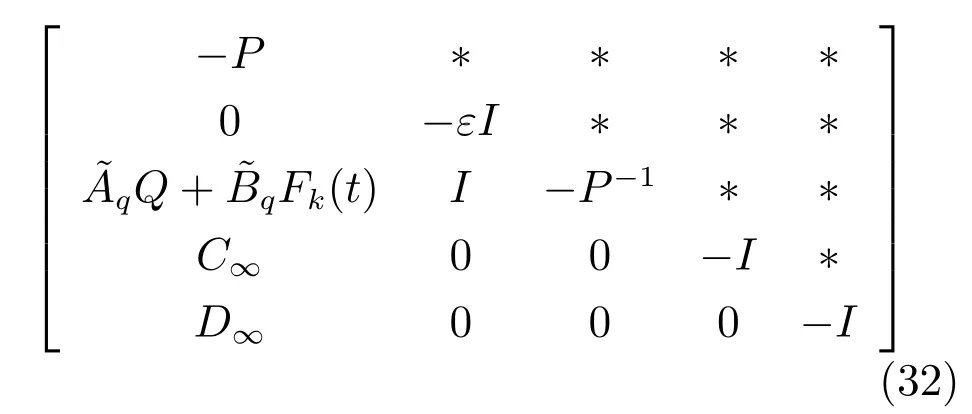
分别左乘右乘diag{P−1,I,I,I,I},得

将P=γQ−1,Fk(t)=Y Q−1代入式(33),式(31b)可以被推出.

注意式(26)为式(25b)的充分条件,也就是说只需要要满足式(26),式(25b)也能被满足.将P=γQ−1代入式(27),利用Schur 补定理,即可得到矩阵不等式(31c).

根据优化得到的Fk(t),通过下式计算控制输入uk(t):

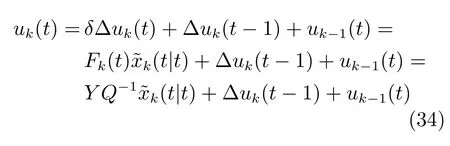
其中,∆uk(t −1)、uk−1(t)为当前批次当前时刻的已知量.等于当前状态

2.4 控制输入约束

间歇过程中需要考虑的控制输入约束包括uk(t)、∆uk(t)和δuk(t),通常表述为

推导uk(t),∆uk(t),δuk(t)与δ∆uk(t)的关系

从式(36)可以看出,uk(t),∆uk(t),δuk(t)都可以表示成δ∆uk(t)与其他已知量的和的形式.将其表述为以下通式

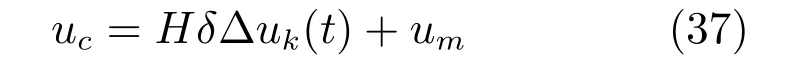
其中,uc是被约束量,um是已知量,H是用于选择δ∆uk(t)中某一控制输入的向量.

式(35)中的约束条件可以统一表述为

其中,µ代表约束上界.

结合式(37),对不等式(38)进行放缩

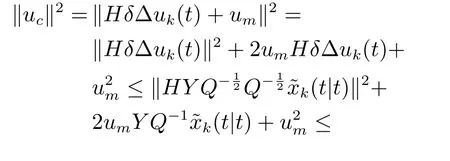
因此控制输入约束下的鲁棒迭代预测控制优化问题可以描述为:

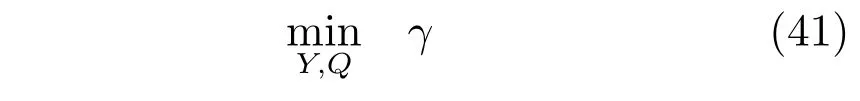
满足式(31b),式(31c),式(40).

3 收敛性分析

MPILC 控制系统的收敛性指的是当迭代次数趋近于无穷时,跟踪误差收敛到零,即对于任意t ∈[0,N],当k →∞时,ek(t)→0.文献[29]在xk−1(N)=xk(0)的前提下,证明了经典MPILC算法的收敛性.而近年研究中,设计附加条件使成为保证收敛性更为常用的方法[9,11].在本文提出的RMPILC 算法中,基于包含参考轨迹变化量的LPV 模型(7),可以转化为有关增广状态T的约束,将其加入到实时优化中,就可以保证原非线性系统在RMPILC控制下沿迭代轴的收敛性.

首先,提出以下符合实际过程情况的假设:

1)优化问题(31)在初始时刻可行;

2)对于t ∈[0,N −1],存在满足约束式(31b),式(31c),式(40)的控制序列uk(t)令跟踪误差ek(t+1)等于0;

3)在t时刻,已知t+1 时刻的参考轨迹变化量.

定理1.若在每个采样时刻的优化中,对于q=1,2,···,l,j=1,2,···,ny满足LMI 约束

证明.在当前时刻t,为保证下一时刻的跟踪误差沿迭代轴收敛,即-,应满足以下不等式条件:

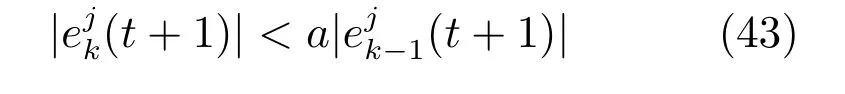
其中,j=1,2,···,ny.

根据式(5)有

联立式(5)和(6)得

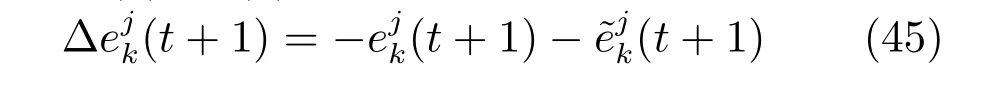
联立式(43)、(44)和(45)可以得到

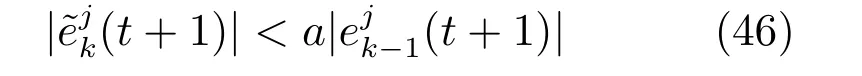
为不等式(43)的充分条件.(46)可以转化为系统(7)的状态约束:

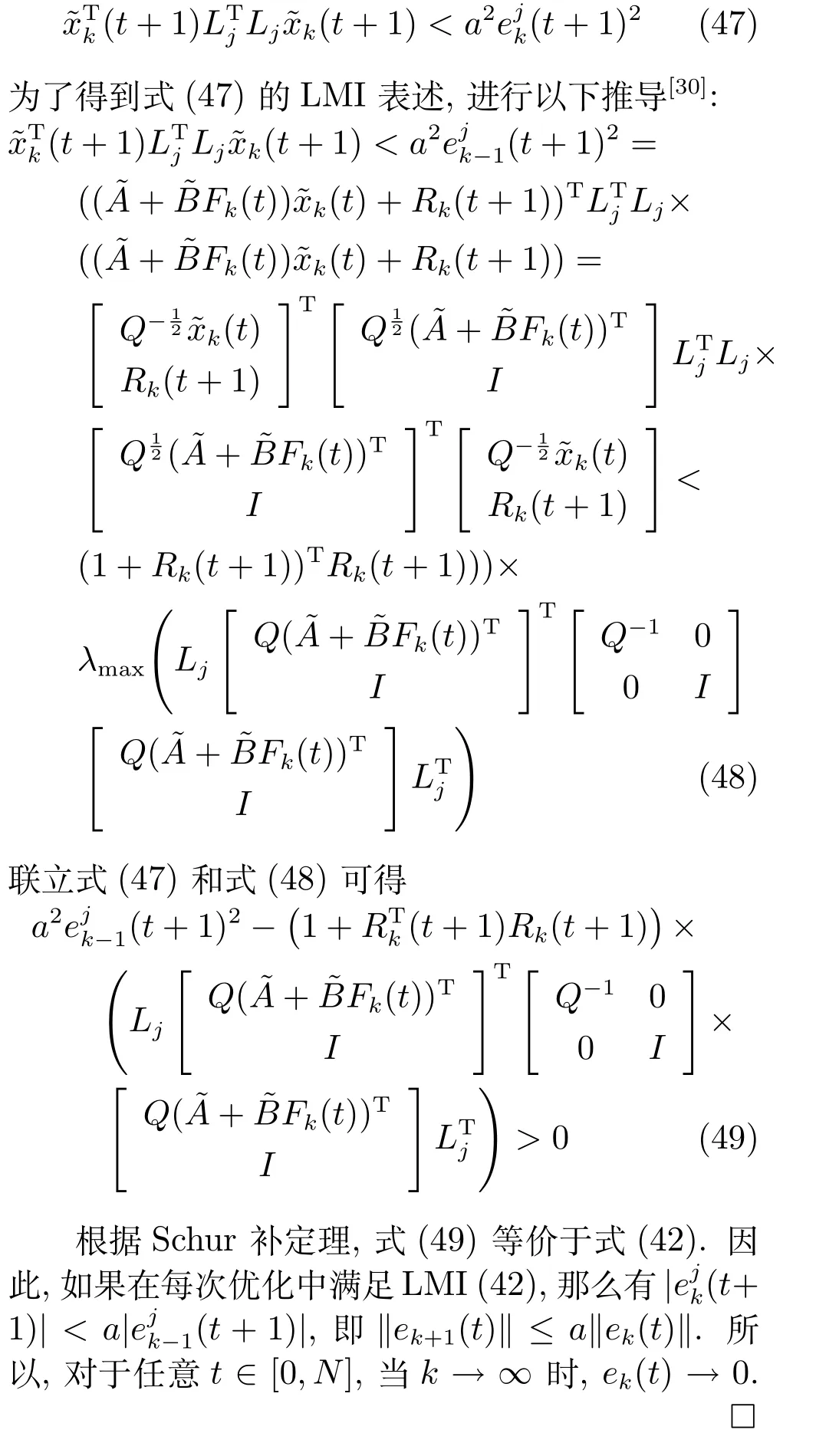
4 仿真研究

本节设计两组仿真实验以验证所提出的RMPILC 在处理变轨迹跟踪问题方面的有效性.仿真1 针对非线性数值系统,侧重于对算法的理论分析和验证;仿真2 针对典型的间歇CSTR 系统,侧重于对RMPILC 的实际应用效果检验.为进行对比,同时设计经典MPILC 算法的仿真实验,其预测模型为:

gi,j ∈Rny(i)×nu(j)为j时刻施加的单位脉冲信号输入在i时刻的脉冲响应矩阵.通常矩阵G可以通过沿参考轨迹进行线性化得到.经典MPILC 算法的目标函数为:

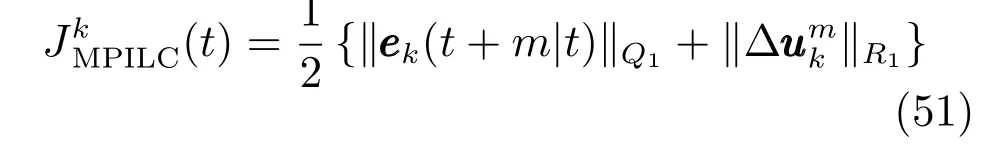
其中,Q1和R1为权重系数矩阵.

4.1 仿真1

考虑如下非线性数值系统

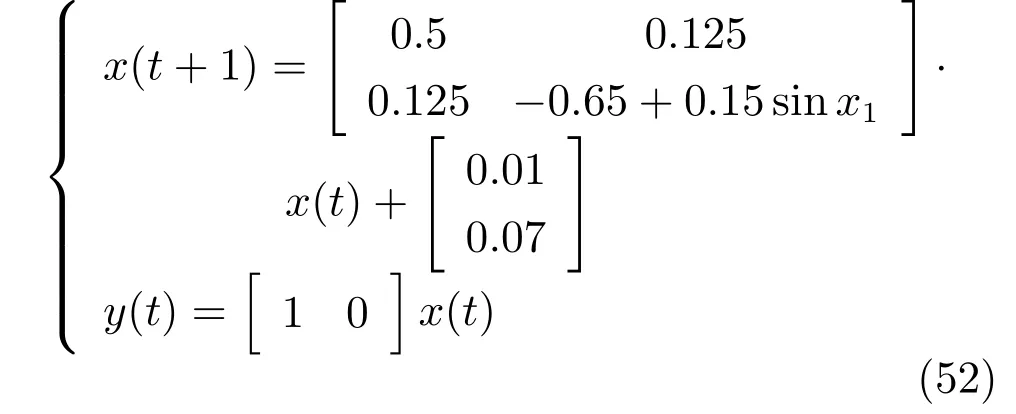
控制输入约束为

根据式(7),可以得到

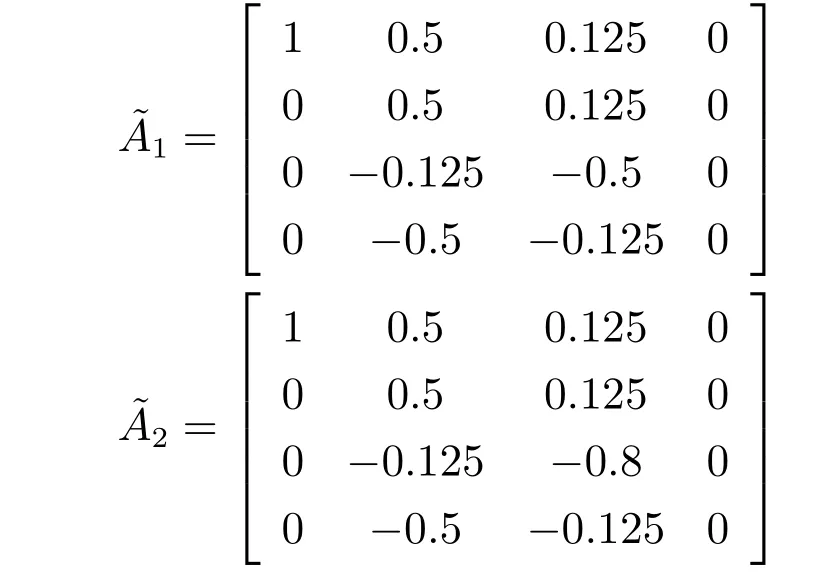
仿真设置两种参考轨迹如图1 所示.第1 批次到第4 批次的目标参考轨迹为yr1;从第5 批次开始,目标参考轨迹变为yr2.仿真时间为10 分钟,采样时间为0.025 分钟.批次长度为400.第1 批次的控制输入为零向量.H∞性能上界ε设为10.初始状态为x(0)=[0,0]T.收敛条件(42)作为每次优化的约束,保证跟踪误差的收敛性,其中a=0.9.权重矩阵取为

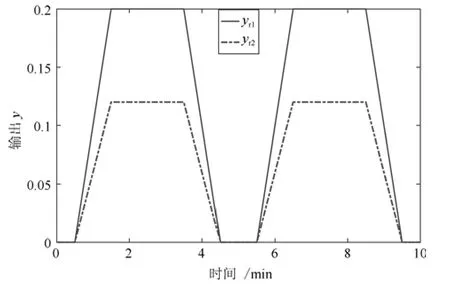
图1 参考轨迹yr1, yr2Fig.1 The reference trajectories yr1, yr2

在每个采样时刻,通过求解约束(42)下的LMI优化问题(41)得到变量Y,Q,继而通过式Fk(t)=Y Q−1计算当前时刻的状态反馈矩阵Fk(t).仿真分析中选择参考轨迹转折点第61 个采样时刻来比较变轨迹前后的状态反馈矩阵变化,其结果如表1 所示.图2 和3 为RMPILC 的跟踪曲线及对应的控制输入曲线.

在经典MPILC 仿真中,设置Q1=I400×400,R1=0.00015I20×20,m=20.其跟踪曲线如图4 所示.

表1 Fk(t)优化值Table 1 Optimized feedback control law

图2 RMPILC 控制下参考轨迹跟踪曲线Fig.2 The tracking trajectories under RMPILC

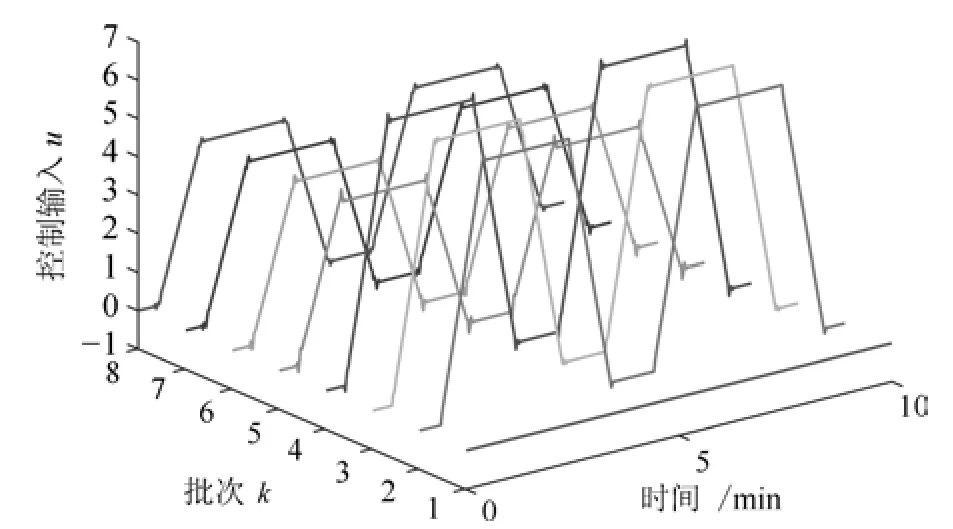
图3 RMPILC 控制下控制输入轨迹Fig.3 The control input trajectory under RMPILC

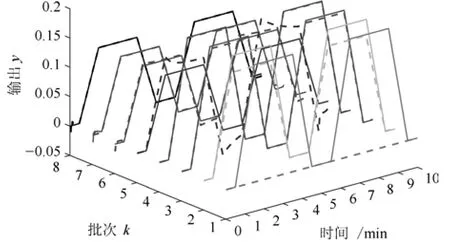
图4 MPILC 控制下参考轨迹跟踪曲线Fig.4 The tracking trajectories under MPILC

比较图2 和图4,在参考轨迹保持不变的第1∼第4 批次,RMPILC 从第2 批次就能够精确跟踪yr1,而MPILC 直到第4 批次才能较好地跟踪yr1.这是因为RMPILC 采用了LPV 模型来描述原系统的非线性特性,避免出现模型失配问题,从而获得了更快的收敛速度;在参考轨迹变为yr2的第5∼第8 批次,RMPILC 能快速跟踪yr2,而MPILC难以及时适应变参考轨迹,需要经过几次迭代才能达到较好的跟踪效果.因而,RMPILC 采用H∞控制有效抑制了变参考轨迹的影响.

图5 为RMPILC 和经典MPILC 控制下各批次跟踪误差均方差(Main square error,MSE)的变化情况.RMPILC 控制下MSE 沿迭代轴收敛到零,且在参考轨迹变化的第5 批次,没有明显波动,保持收敛趋势,而MPILC 控制下MSE 出现较大波动.这证明了RMPILC 在变参考轨迹下能够保证跟踪误差沿迭代轴收敛.

图5 MPILC 和RMPILC 控制下MSE 随批次变化情况Fig.5 The MSE along batches under MPILC and RMPILC

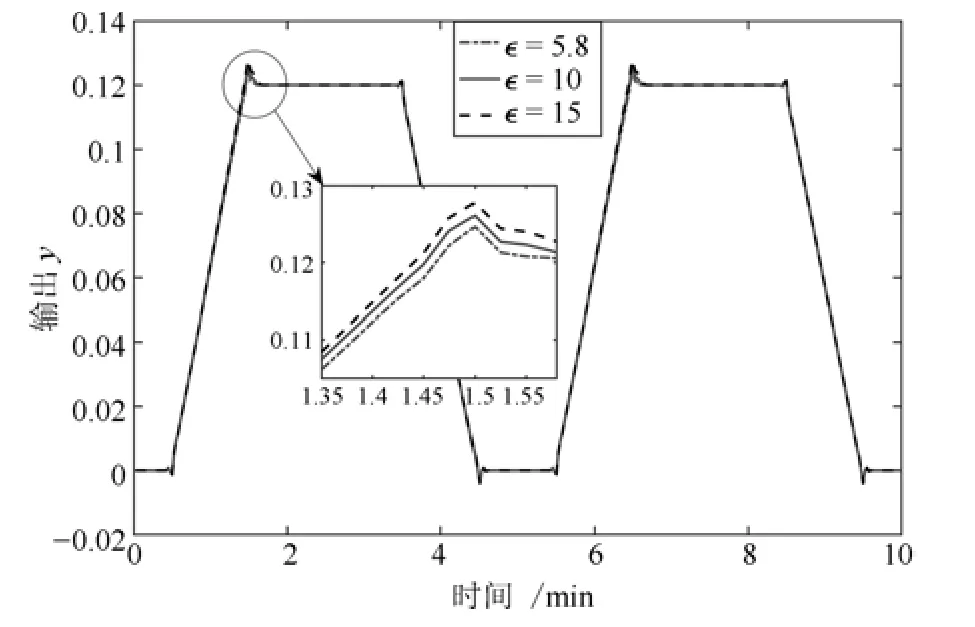
图6 RMPILC 控制下第5 批次当ε=5.8、ε=10 和ε=15 时的跟踪曲线Fig.6 The tracking trajectories in the fifth batch when ε=5.8,10,15

RMPILC 的控制性能与参考轨迹变化程度以及H∞性能上界ε的大小有较大关系.由式(11)可知,ε越小越有利于增强抗干扰能力.而式(26)表明ε减小将导致可行域的缩小.当可行域缩小到不能包含当前状态时,优化问题将无解.因此,在选择ε时,要根据实际需要权衡变轨迹适应能力和可行性问题.对于系统(52)能够保证可行性的最小ε值为5.8.图6 为参考轨迹发生变化的第5 批次中,RMPILC 在ε=5.8、ε=10 和ε=15 时的跟踪情况,表明随着ε增大,RMPILC 跟踪性能下降.图7 为x(0)=[0.01,0.05]T,ε分别取值5.8、10 和15时不变集Ω˜xk={x|xTQ−1x ≤1}在原状态空间的象集.由于不变集的大小能够反映可行域的大小,因此图7 表明初始可行域随ε减小而缩小.

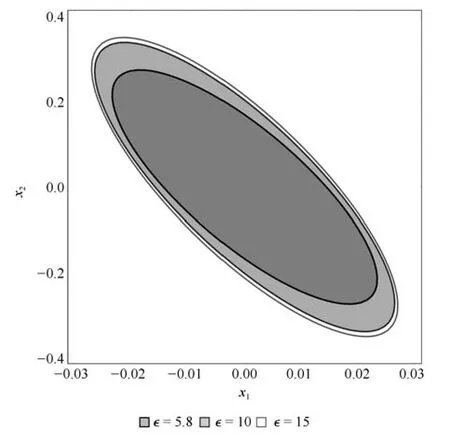
图7 RMPILC 控制下ε=5.8、ε=10 和ε=15 时的不变集 在原状态空间的象集Fig.7 The image set of when ε=5.8,10,15

4.2 仿真2:CSTR 系统

连续搅拌反应釜系统中进行恒定体积、放热、不可逆化学反应A →B.其控制任务为重复跟踪给定的反应温度轨迹,且生成物B的产品质量很大程度依赖于跟踪精度.因此,采用MPILC 方法控制CSTR 系统能适应其生产过程的重复性,并且提高产品质量.

CSTR 系统具有以下非线性微分方程描述[31]:

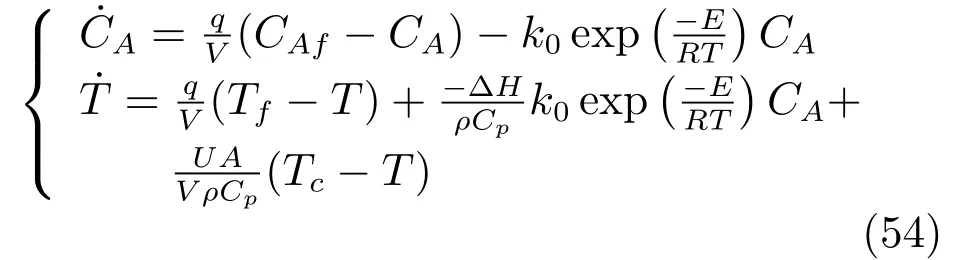
其中,反应温度T(K)为被控量,冷却剂温度Tc(K)为控制输入.其他参数的物理意义和取值见文献[31].

在间歇反应器控制中,反应温度T的参考轨迹可能会由于调整进料浓度CA、启动速度、批次时间长度等发生变化.为了验证RMPILC 在适应频繁变化的参考轨迹的能力,在仿真中设置三种不同的参考轨迹,如图8 所示,包括常规轨迹yr1、慢启动轨迹yr2以及快启动轨迹yr3.yr3中T上升较快,有利于提高产量;yr2中T上升较慢,后续反应更加平稳,易于控制.在实际生产中可以根据不同的生产需求选择不同的参考轨迹.

根据文献[32]介绍的替换法,非线性系统(54)可以表述为如式(2)的LPV 模型,过程如下:

首先,计算系统(54)的平衡点:

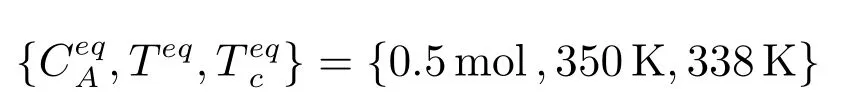
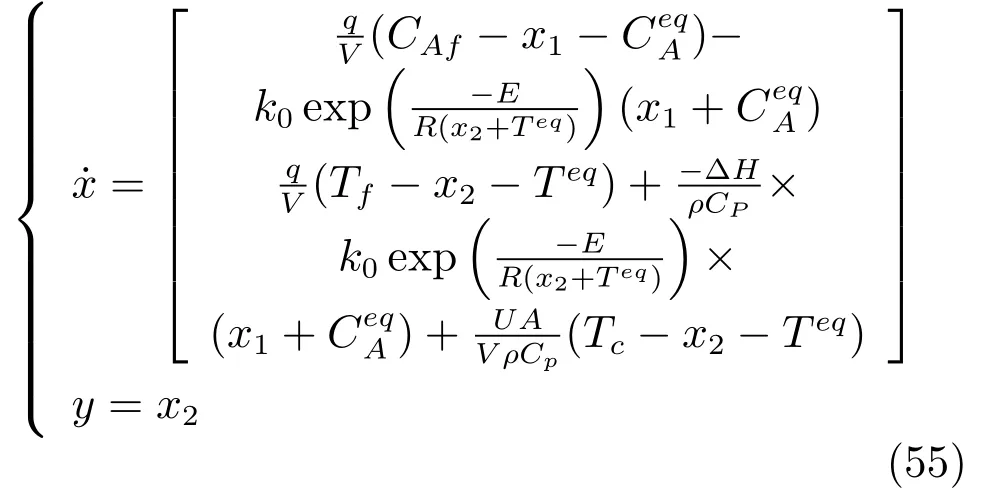
图8 CSTR 反应温度T 参考轨迹Fig.8 The reference trajectories of CSTR reaction temperature T

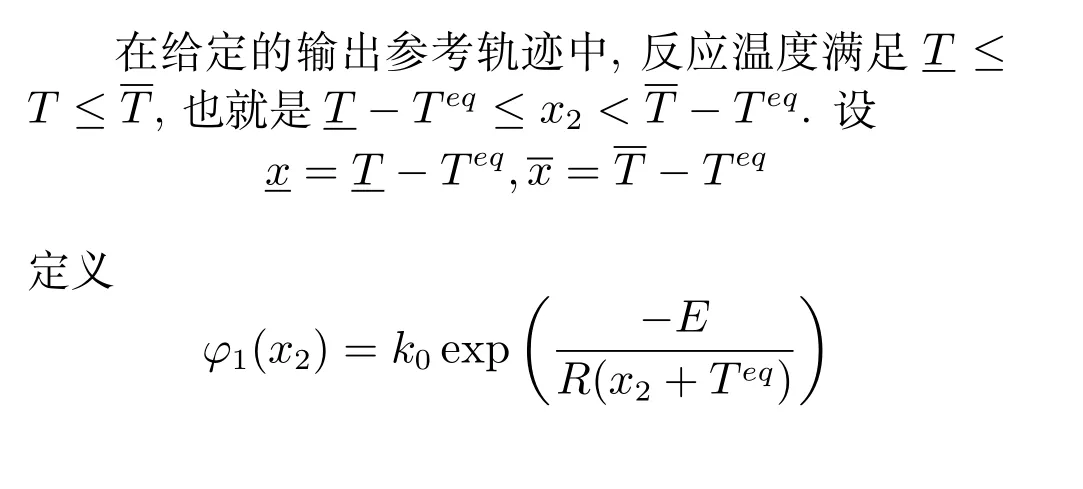
选择LPV 模型(2)中的参数θ为

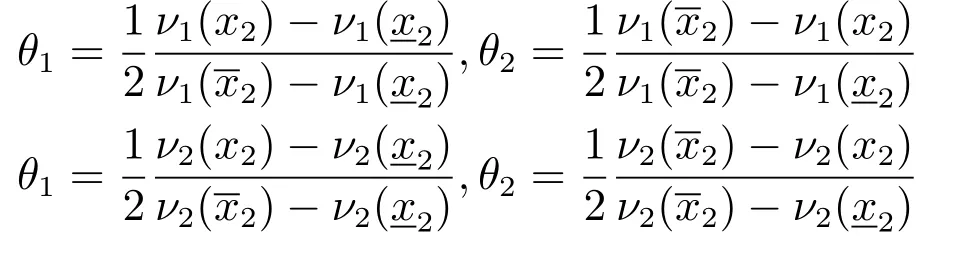
那么系统(55)可以由如式(2)的LPV 模型描述,其多胞形的各顶点为

仿真基于LPV 模型设计控制律,并将优化得到的控制输入施加都原非线性系统(54)中.

控制输入Tc的约束如下:

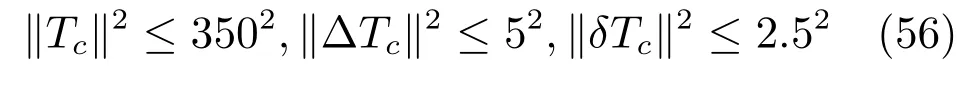
仿真时间为12 分钟(min),采样时间为0.03分钟(min),批次长度为400.设置初始参考轨迹为yr1,在第6 批次、第7 批次分别变为yr2、yr3,在第8 批次变回yr1.批次1 的初始控制输入为幅度为330 K 的阶跃信号.初始状态为[CA,T]T=[0.7 mol/L,340 K]T.H∞性能上界选为ε=20.权重系数矩阵选取同仿真1.同样地,收敛条件(42)在每次优化中作为约束(a=0.9),状态反馈矩阵Fk(t)由Fk(t)=Y Q−1计算得到,各批次Fk(200)的优化值如表2 所示.

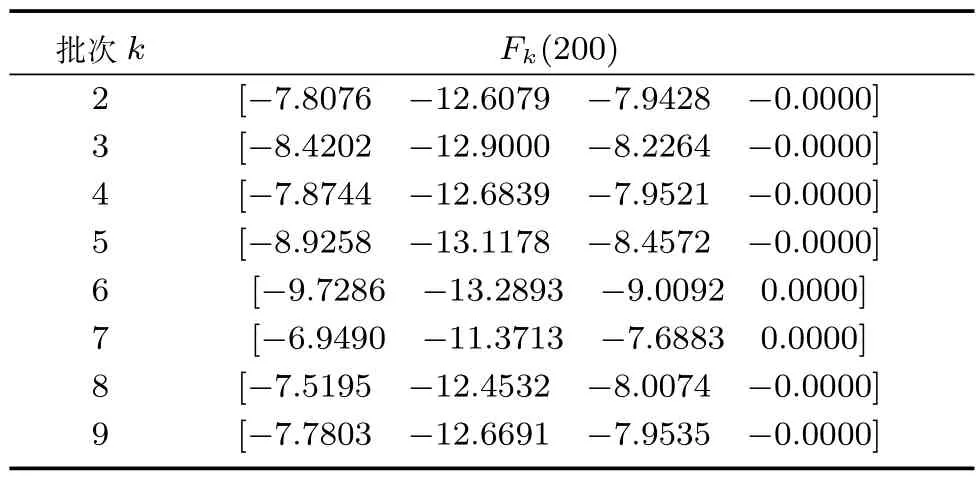
表2 Fk(t)优化值Table 2 Optimized feedback control law

在经典MPILC 仿真中,设置m=10,Q1=I400×400,R1=I10×10.图9 和-图11为RMPILC 和MPILC 控制下的跟踪曲线.相应的RMPILC 控制输入如图10 所示.可以看出RMPILC 从第2 批次开始就可以准确跟踪yr1,且在批次6∼8 能够及时跟踪变化轨迹.而MPILC 直至批次5 才能跟踪上yr1,且在批次6∼8 不能适应参考轨迹变化.因此与经典MPILC 相比,基于LPV 模型的RMPILC 快速跟踪变参考轨迹,有利于提高CSTR 的生产效率.

图9 RMPILC 控制下反应温度T 参考轨迹跟踪曲线Fig.9 The tracking trajectories for T under RMPILC control

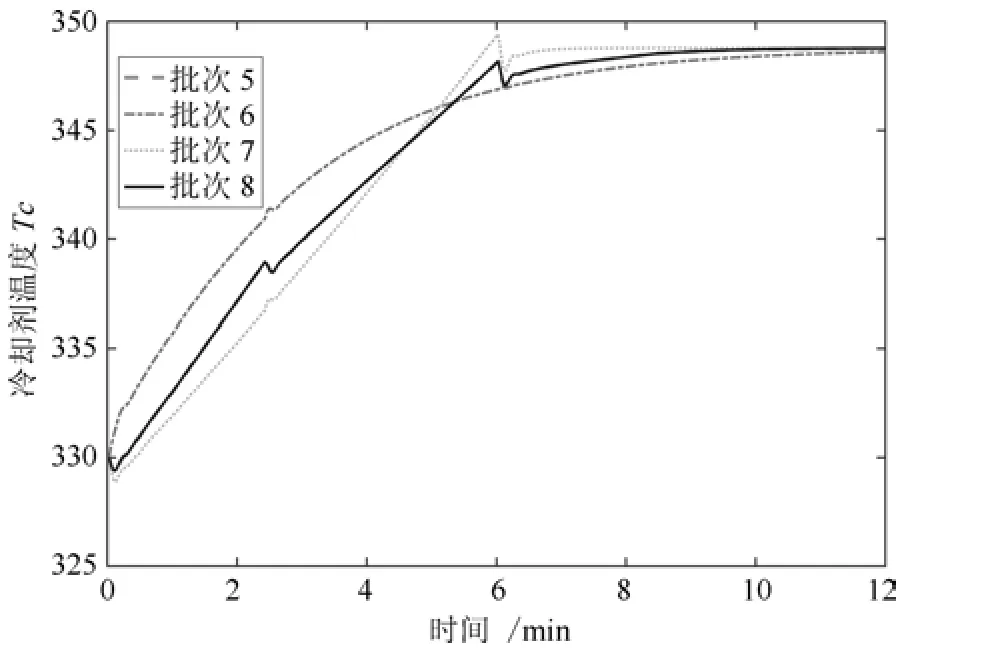
图10 RMPILC 控制下控制输入Tc 轨迹Fig.10 The trajectories of control input Tc under RMPILC

图12 为变轨迹下RMPILC 和MPILC 仿真中MSE 随迭代次数的变化情况.显然,变参考轨迹下RMPILC 的跟踪误差沿迭代轴收敛,而MPILC 的跟踪误差发生较大波动,会导致产品质量下降.

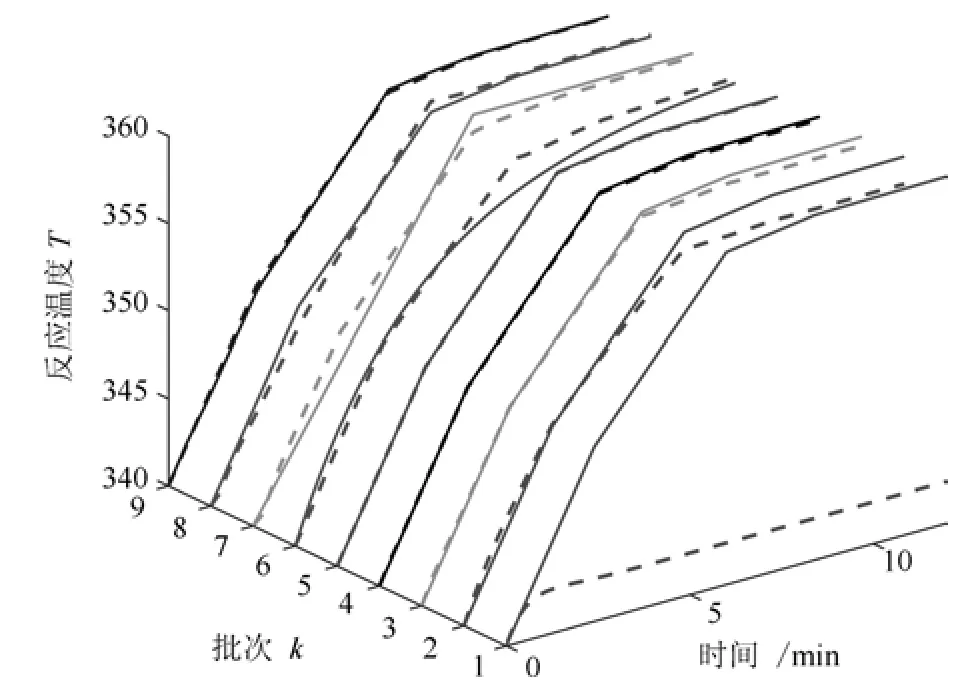
图11 MPILC 控制下反应温度跟踪曲线Fig.11 The tracking trajectories for T under MPILC

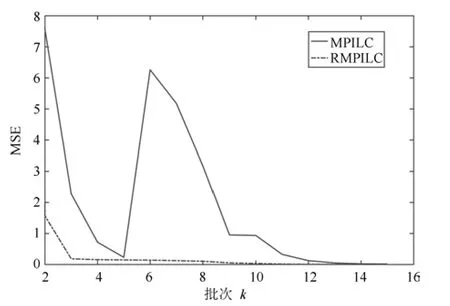
图12 RMPILC、MPILC 控制下MSE 随批次变化情况Fig.12 The MSE along batches under RMPILC and MPILC

5 结束语

本文针对具有重复特性的非线性间歇过程,提出一种能跟踪变参考轨迹的鲁棒迭代学习模型预测控制.控制器设计基于包含被控系统非线性动态特性的LPV 模型,将LPV 模型进行状态增广建立二维迭代误差模型.在鲁棒H∞预测控制框架下,设置H∞性能上界,并据此构建LMI 约束下的目标函数优化问题.分析RMPILC 系统的鲁棒稳定性和迭代收敛性,将其充分条件作为约束加入每个采样时刻的优化中.仿真结果验证了RMPILC 在快速跟踪变参考轨迹方面的优势,表明采用基于LPV 模型的RMPILC 算法能显著减少迭代学习次数,提高生产效率.

在实际生产中,间歇过程的参考轨迹可能会发生剧烈变化.若要保证鲁棒稳定条件和迭代收敛条件,可能会导致优化问题不可行,或是可行域太小以至达不到期望的跟踪精度.因此,未来的研究方向趋向于构建软约束RMPILC 算法.在优化中引入松弛变量来放松约束,允许控制输入在短时间内超出约束以达到扩大可行域的目的[33].基于软约束的RMPILC 算法将能够适应剧烈变化的参考轨迹,提高间歇过程控制的鲁棒性.