用于灰度不均图像分割的自适应灰度拟合模型

张栩源 王艳

摘 要：针对灰度不均图像的分割问题，提出了一个结合全局信息的局部区域自适应灰度拟合模型。首先，分别利用图像的局部和全局信息构造了局部拟合项和全局拟合项;其次，利用像素点邻域内灰度的极差反映该点邻域内灰度的偏差程度，并以此定义了一个自适应权值函数;最后，利用定义的权值函数为局部项和全局项自适应赋权值，得到所提模型的能量泛函，并使用变分法推导出模型的水平集函数迭代方程。数值实现采用有限差分法。实验结果表明，与区域可变灰度拟合（Region-Scalable Fitting， RSF）模型和局部和全局灰度拟合（Local and Global Intensity Fitting， LGIF）模型相比，所提模型不仅能够稳定、准确地分割多种灰度不均图像，而且对演化曲线初始轮廓的位置、大小和形状具有更强的鲁棒性。

关键词：图像分割;自适应权值;局部区域信息;灰度不均图像;水平集方法

中图分类号：TP391.41

文献标志码：A

Adaptive intensity fitting model for the segmentation of images with intensity inhomogeneity

Adaptive intensity fitting model for segmentation of images with intensity inhomogeneity

ZHANG Xuyuan， WANG Yan*

School of Mathematical Sciences， Chongqing Normal University， Chongqing 401331， China

Abstract：

For the segmentation of images with intensity inhomogeneity， a region-adaptive intensity fitting model combining global information was proposed. Firstly， the local and global terms were constructed based on local and global image information respectively. Secondly， an adaptive weight function was defined to indicate the deviation degree of the gray scale of a pixel neighborhood by utilizing the extreme difference level in the pixel neighborhood. Finally， the defined weighting function was used to assign weights to local and global terms adaptively to obtain the energy functional of the proposed model and the iterative equation of the models level set function was deduced by the variational method. The experimental results show that the proposed model can segment various inhomogeneous images stably and accurately in comparison with Region-Scalable Fitting （RSF） model and Local and Global Intensity Fitting （LGIF） model， which is more robust in the position， size and shape of initial contour of evolution curve.

Key words：

image segmentation; adaptive weight; local region information; intensity inhomogeneous image; level set method

0 引言

圖像分割是计算机视觉领域的基本问题之一，目的是将图像的目标从背景区域中提取出来。图像的种类繁多，其中，灰度不均图像广泛存在于生产生活中，如医学图像（X线图像、磁共振（Magnetic Resonance， MR）图像）、遥感图像（热红外图像）等，这些图像都包含了丰富的信息。然而，由于目标和背景区域的灰度都是不均匀的，增加了分割灰度不均图像的难度。灰度不均图像的分割问题已成为如今研究的热点问题，受到国内外学者的广泛关注[1-5]。

几何活动轮廓模型是分割灰度不均图像较为常用的方法之一。它将二维空间上的活动轮廓隐含地表示为一个高维空间曲面的零水平集，水平集函数在一个偏微分方程的控制下演化，直到零水平集演化到图像的目标边界。这类模型不仅能够处理拓扑结构的变换，而且计算精确度高、稳定性好。

几何活动轮廓模型一般可分为两类：基于边缘的模型和基于区域的模型。前者利用图像的边界信息（如图像的梯度）引导曲线演化，后者利用区域信息控制曲线的移动。本文主要关注后者。Chan等[6]提出的分片常值（Piecewise Constant， PC）模型是一个著名的区域模型（常被称为CV模型），该模型在分割弱边界图像时取得了很好的效果，而且对初始轮廓的位置不敏感。然而，由于该模型主要依靠图像的全局信息，因此对灰度不均图像的分割效果并不理想。为了弥补CV模型的缺陷，Li等[7-8]利用高斯核函数将图像的局部信息融入到模型的设计中提出了区域可变灰度拟合（Region-Scalable Fitting， RSF）模型 ，该模型能有效地对灰度不均图像进行分割。然而，该模型对活动轮廓的初始化较为敏感。

针对这个问题，很多学者从不同角度提出了有效的解决办法。如文献[9]将图像点的局部熵作为权系数融入到RSF模型的拟合能量中，所提模型有效地降低了对初始轮廓的敏感性;Wang等[10]提出了局部和全局灰度拟合（Local and Global Intensity Fitting， LGIF）模型，该模型同时考虑全局信息和局部信息，不仅增强了模型分割灰度不均图像的能力，而且提高了对初始轮廓的鲁棒性。Zhang等[11]提出了局部统计活动轮廓模型（Locally Statistical Active Contour Model， LSACM），利用高斯分布和极大似然函数作为能量拟合项，对灰度不均图像取得了很好的分割效果。

为了灵活地利用图像的全局和局部信息，学者们提出了不同的权值系数对它们进行融合。文献[12]将演化曲线内外区间的灰度均值差提出一个新的权重函数，以此连接全局和局部信息;文献[13]将最大类间方差引入局部图像拟合（Local Image Fitting， LIF）模型[14]中，并利用图像的局部熵对全局和局部信息的权重赋值;文献[15]基于局部对比度提出了一个权函数，来调整全局项在模型中的权重。

受文献[15]的启发，本文在LGIF模型的基础上提出一个新的自适应灰度拟合活动轮廓模型用于灰度不均图像的分割。本文模型利用局部区域内灰度的极差量化其离散度，并以此定义了一个自适应变化的权值函数，根据灰度不均程度对能量泛函中的全局和局部信息进行自适应赋权值。实验表明，该模型能够根据图像特征自适应调整权函数的取值，不仅能够分割灰度不均图像，而且在权重参数固定的情况下，对初始轮廓的位置、大小和形状具有更强的鲁棒性。

1 相关模型

1.1 CV模型

CV模型假定图像I（x）由两个平均灰度相差较大的同质区域（目标和背景）组成，因此通过一个二值分段函数来近似原始图像，其水平集形式的能量泛函为：

ECV（，c1，c2）=λ1∫Ω|I（x）-c1|2Hε（（x））dx+

λ2∫Ω|I（x）-c2|2（1-Hε（（x）））dx+

ν∫Ωδε（）||dx=εCV（，c1，c2）+νL（）（1）

其中：是水平集函数，x=（x，y）是图像区域Ω中的某一点。对于每个，常值c1和c2分别为演化过程中图像在曲线内部（{≥0}）和外部（{<0}）的平均灰度值，这是与图像的全局信息有关，没有包含图像的局部信息。λ1、λ2和ν为权重系数。Hε（x）和δε（x）分别是正则化的Heaviside函数和Dirac函数，通常定义为：

Hε（x）=121+2π arctanxε（2）

δε（x） = H′ε（x） = 1π·εε2 +x2（3）

其中参数ε=1。

固定，关于c1和c2极小化能量泛函（1），得到：

c1（）=∫Ω I（x）H（（x））dx

∫ΩH（（x））dx（4）

c2（）=∫Ω I（x）（1-H（（x）））dx

∫Ω（1-H（（x）））dx（5）

在式（1）中，前两项作为能量拟合项驱使演化曲线向目标边界移动，当演化曲线到达目标边界时，能量泛函取得最小值。然而，当CV模型处理灰度不均图像时，演化曲线内外的图像灰度并不均匀，所以，由式（4）和式（5）计算得到的c1和c2会偏离原始图像灰度值，导致模型的全局拟合项误差较大。因此，CV模型对灰度不均图像的分割效果并不理想。

1.2 RSF模型

不同于CV模型，RSF模型是一个基于区域可变灰度拟合能量的局部区域模型。对于图像域中的某一点x=（x，y），其水平集形式的能量泛函为：

εFit=（， f1（x）， f2（x））=

∑2i=1λi ∫（∫Kσ（x-y）|I（y）-

fi（x）|2 Mi（（y））dy）dx（6）

其中：M1（）=Hε（），M2（）=1-Hε（）。y是圖像点x的邻域内的一点， fi（x）（i=1，2）为图像以点x处为中心的邻域内的局部灰度拟合值。Kσ为高斯核函数，σ>0为控制局部区域大小的尺度参数。为了保证水平集函数在演化过程中的稳定性，模型增加了长度项L（）和水平集正则化项P（）[16]。于是，由水平集表示的RSF能量泛函为：

ERSF（， f1， f2）=εFit（， f1， f2）+ν∫δ（）||dx+

（μ/2）∫（||-1）2dx=

εFit（， f1， f2）+νL（）+

μP（）（7）

其中ν≥0、 μ>0为权重系数。

固定，关于f1（x）和f2（x）极小化能量泛函（7），得到：

f1（x）=Kσ（x）*[M1（（x））I（x）]

Kσ（x）*M1（（x））（8）

f2（x）=Kσ（x）*[M2（（x））I（x）]

Kσ（x）*M2（（x））（9）

在RSF模型中， f1和f2分别为图像在演化曲线内外高斯窗口内图像灰度的加权平均值。这两个拟合函数利用了像素点邻域内的图像信息，因此，该模型能够有效地分割灰度不均图像。然而，该模型对于初始轮廓的位置和大小都较为敏感，不同的初始轮廓可能产生不同的甚至是错误的分割结果，这在一定程度上影响了该模型的应用。

1.3 LGIF模型

为了解决RSF模型对初始轮廓敏感的问题，文献[10]结合图像的全局和局部灰度信息，提出了一个新的活动轮廓模型，即LGIF模型。该模型的能量泛函是通过一个常值权重系数将全局灰度拟合项和局部灰度拟合项进行线性组合，其水平集形式表示为：

EIGIF（， f1， f2，c1，c2）=μP（）+νL（）+

ωεCV（，c1，c2）+

（1-ω）εFit（， f1， f2）（10）

其中，ω是一个取值在[0，1]上的常值权重系数，调整全局项和局部项的比重。模型在处理灰度不均图像时，取较小的ω值可以突出局部信息的作用。然而，不同的图像灰度不均程度各不相同，模型需要根据情况选择合适的ω值。手动调整耗时费力，而且参数区间的跨度可能很大，对于同一幅图像的不同初始轮廓有时很难找到公共参数值。这在一定程度上影响了该模型对灰度不均图像的分割效率。

2 本文模型

2.1 自适应权值

为了量化图像灰度变化的程度，文献[15]首先定义了图

像的局部对比度：

CN（x）=（Mmax-Mmin）/Mg（11）

其中：N表示以点x=（x，y）为中心的局部计算窗口的大小，Mmax和Mmin分别表示局部窗口内图像灰度的最大值和最小值，Mg表示整幅图像的灰度级。对于灰度图像，通常取Mg=255。CN（x）∈[0，1]，在同质区域的取值较小，在目标的边缘处取值较大。

基于式（11），文献[15]最终定义了如下的权函数：

ω（x）=γ·average（CN）·（1-CN）（12）

其中：average（CN）为整幅图像的CN的平均值，1-CN用于调整全局项在图像区域内的权重。γ=0.1是一个固定参数。ω（x）在CN越大的区域函数值越小，在CN越小的区域函数值越大。

受文献[15]的启发，本文同时考虑全局和局部灰度信息的极差，提出了一个新的局部对比度：

RN（x）=（Mmax-Mmin）/（Imax-Imin）（13）

其中，Imax和Imin分别表示整幅图像的灰度的最大值和最小值。显然，RN（x）∈[0，1]。它反映了局部区域灰度的离散程度。在图像灰度较均匀的区域，邻域内灰度的极差较小，而在灰度不均匀的区域，其灰度的极差较大。同时考虑整幅图像灰度的极差，以此突出灰度变化的程度。式（11）是式（13）在图像的最大灰度值为255，最小值为0的情形。与式（11）相比，式（13）更细致地量化图像的灰度不均，对灰度不均区域更加敏感。

于是，新的权值系数定义如下：

ρ（x）=θ·average（RN）·（1-RN）（14）

其中θ是一个固定参数。通过大量的实验验证，本文模型中参数θ=0.375。 ρ（x）能够量化图像灰度的变化幅度，根据图像灰度变化的强弱自适应调整函数值，在灰度变化较大的区域，ρ（x）的取值接近0。相比固定的常值系数ω，最终的权值函数（14）能够自适应图像的灰度特征，增加分割的准确性。

下面给出本文模型自适应权值的计算步骤：

步骤1 对初始图像I计算最大和最小灰度值，得到Imax和Imin;

步骤2 以图像点x=（x，y）为中心，取大小为N×N的局部计算窗口，计算窗口内的最大和最小灰度值，得到Mmax和Mmin，根据式（13）计算该点的局部对比度RN（x）;

步骤3 计算整幅图像每个点的RN，取算术平均值得到average（RN），根据式（14）计算每个图像点的权值ρ（x）。

2.2 模型描述

本文利用自适应权值（14）连接图像的全局拟合项和局部拟合项，提出一个新的自适应灰度拟合活动轮廓模型。其能量泛函的水平集表示为：

E（， f1， f2，c1，c2）=（1-ρ（x））εFit（， f1， f2）+

ρ（x）εCV（，c1，c2）+μP（）+νL（）（15）

在靠近目标边界以及其他灰度不均匀的區域，图像的灰度变化较大，因此，Mmax与Mmin的差值较大，RN（x）的值也会较大，所以ρ（x）会较小。此时，本模型弱化全局项的作用，突出局部项的作用，保证分割的准确性。相反，当图像的灰度变化较小时，如在同质区域，Mmax与Mmin的差值较小，RN（x）的值也会较小，所以ρ（x）会较大。此时，本模型弱化局部项的作用，同时加速曲线的演化。

固定c1和c2、 f1和f2，利用变分法和梯度下降流，对水平集函数极小化能量泛函（15），可以得到关于的欧拉拉格朗日方程：

t=δ（）（F1+F2）+νδ（）div（/||）+

μ[Δ-div（/||）]（16）

其中：

F1=ρ（x）[-λ1|I（x）-c1|+λ2|I（x）-c2|2]

F2=（1-ρ（x））[-λ1∫Kσ（y-x）|I（x）-f1（y）|2dy+

λ2∫Kσ（y-x）|I（x）-f2（y）|2dy]

（17）

2.3 数值实现

本文采用有限差分的方法求解微分方程（16），对所有空间域上的偏导数用中心差分的方法近似，时域上的偏导数用向前差分的方法近似。离散网格的空间步长为h，时间步长为Δt。水平集函数在n时刻网格点x=（x，y）处可表示为（nΔt，ih， jh）（记为ni， j），式（16）的离散化形式为：

n+1i， j=ni， j+Δt·{δ（ni， j）（F1（ni， j）+F2（ni， j））+

νδ（ni， j）div（ni， j/ni， j）+

μ[Δni， j-

div（ni， j/ni， j）]}（18）

其中，div（/）为曲率curv=div（/）的离散形式，一般用二阶中心差分的方法近似，具体表达式为：

curv=div（ni， j/ni， j）=xx2y-2xyxy+yy2x（2x+2y）3/2（19）

其中：x、y为一阶中心差分，xx、yy、xy为二阶中心差分，各自的表达式为：

x=12h（i+1， j-i-1， j）

y=12h（i， j+1-i， j-1）

xx=（1/h2）（i+1， j+i-1， j-2i， j）

yy=（1/h2）（i， j+1+i， j-1-2i， j）

xy=（1/h2）（i+1， j+1-i-1， j+1-i+1， j-1+i-1， j-1）

（20）

本文算法使用两次零水平集的面积差作为停止迭代条件，如式（21）：

area（n+ki， j）-area（ni， j）<ξ（21）

其中：area（mi， j）表示第m次迭代计算得到的零水平集曲线所围的面积，ξ是一个极小的正数。收敛状态即停止条件满足时，不再执行迭代并输出n+ki， j，这个收敛状态下的结果就是最终的实验结果。本文模型取k=10，ξ=0.01。

则本文所提模型的算法实现步骤可总结为：

步骤1 初始化水平集函数0（x）=（n=0，x）为一个二值函数。水平集函数在初始轮廓范围内取负值（-c0），其余为正值（c0），即：

0（x）=-c0， x∈Ω0

c0，x∈Ω-Ω0

其中，c0>0为常值，Ω0为图像区域Ω的子区域。

步骤2 由2.1节的计算步骤计算出每个像素点的权值ρ（x）。

步骤3 根据式（4）和式（5）分别计算c1（ni， j）和c2（ni， j），根据式（8）和式（9）分别计算f1（ni， j）和f2（ni， j），根据式（18）迭代计算n+1i， j。

步骤4 迭代计算n+ki， j。

步骤5 检验area（n+ki， j）-area（ni， j）<ξ是否成立：若是，则水平集函数n+ki， j达到收敛并停止迭代;否则，继续迭代直至完全收敛。

步骤6 输出最终结果（x）=n+k（x）。

本文算法的流程图如图1所示。

3 实验结果与分析

本章通过对人造图像、真实图像的分割实验验证本文模型：1）能够分割灰度不均图像;2）全局项和局部项的权重系数允许根据图像特征自适应调整;3）对初始轮廓的位置、大小和形状具有更强的鲁棒性。

实验环境是Matlab R2014a，Windows 7，Intel Core i7-2600，CPU 3.40GHz。实验统一采用空间步长h=1，时间步长Δt=0.1，c0=2，迭代次数上限为1000次。若无特殊说明，本模型使用以下的参数：λ1=λ2=1，σ=3， μ=1，ν=0.001×2552，计算权值函数的窗口大小取为5×5。RSF模型、LGIF模型（除ω外）和LSACM模型的参数各自取其默认值，具体可参考文献[8，10-11]。LGIF模型中ω的取值在实验中具体给出。

3.1 分割灰度不均图像

图2所示是RSF模型、LSACM模型和本文模型对5幅灰度不均图像的分割结果。从图2可以看出，RSF模型和LSACM模型对部分图像的分割效果欠佳，而本文模型都取得了较好的分割结果。

对人造图像2，RSF模型和本文模型的ν取0.005×2552。对医学CT图像，三个模型的σ=7。

表1对比了三个模型分割上述5幅图像的迭代次数。可以看出，LSACM模型对一些图像的分割过程并不稳定。相比于其他模型，本文模型在稳定性上有了较大的提升，迭代次数明显减少。

表2举例说明了本文模型自适应权值的方法。在人造图像1中选取任意不相邻的4个点，计算各自的权值。可以看出，本文提出的权值函数能夠根据像素点位置的不同赋予不同的权值，有效地量化图像灰度不均的程度。

图3以前文的人造图像2和一幅大小为164×164的深度图像为例演示本文模型迭代计算水平集函数的过程以及实验结果。当水平集函数n+k满足式（21）时停止迭代计算，输出n+k并以此作为式（16）的稳定解。从图中可以看到，本文模型以及数值算法能够稳定迭代水平集函数并进行曲线演化。

3.2 初始轮廓位置的鲁棒性

图4是RSF模型、LGIF模型、LSACM模型和本文模型对一幅像素大小为94×122的CT血管造影图像（CTA）的分割结果。图左为初始轮廓的具体位置，大小均为ω的正方形。本实验中，LGIF模型的参数ω的取值区间从上至下依次为[0.018，0.032]、[0.019，0.062]、[0.016，0.024]和[0.035，0.072]，这4个区间并无公共ω值，前3幅图像ω=0.02，第四幅图像ω=0.04，LGIF模型通过调整参数均取得较好的分割结果。LSACM模型对内部轮廓的分割不够细致。本文模型利用自适应权值在这4个位置都能准确稳定分割出目标，受初始轮廓位置的影响较小。

表3是各个模型对应的迭代次数。可以看出，本文模型有着更好的分割稳定性。

3.3 初始轮廓大小的鲁棒性

图5显示了4个模型对一幅像素大小为128×128的大米图像的分割结果，初始轮廓的大小标注在初始轮廓上方。本实验中，LGIF模型的系数ω=0.2。实验结果表明，与RSF模型和LGIF模型相比，对于不同大小的初始轮廓，本文模型都能得到准确的分割结果，对初始轮廓的大小具有更强的鲁棒性。

图6所示在不同大小的圆形轮廓下三种模型的分割结果，初始轮廓的半径标注在初始轮廓上方。LGIF模型在ω=0.05时取得良好的分割结果;LSACM模型在ω=0.05时部分分割结果不够理想;而本文模型均取得满意的实验结果，同时分割得到内部和外部轮廓。

3.4 初始轮廓形状的鲁棒性

RSF模型、LGIF模型、LSACM模型和本文模型对一幅像素大小为ω=0.05的X线血管图像的分割结果如图7所示。本实验选取了矩形和圆形两种不同的初始轮廓，圆形轮廓的迭代上限为8000次，LGIF模型的ω=0.05。可以看出，RSF模型在某些轮廓下出现分割不足的现象。LGIF模型对这五种初始轮廓都能得到满意的分割结果。LSACM模型在圆形轮廓下取得了理想的分割结果，而在方形轮廓的结果均不理想。本文模型无需调整参数，同时分割效果不受轮廓形状的影响，能够较好地分割出目标。表4是各个模型对应的迭代次数，本文模型在方形轮廓下的迭代次数要少于其他模型。

3.5 定量化分析

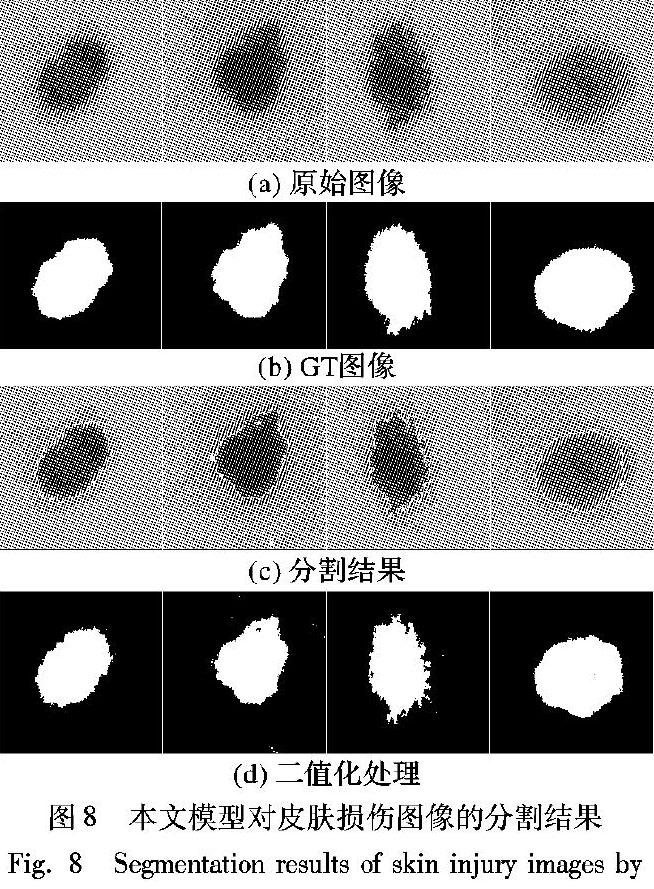
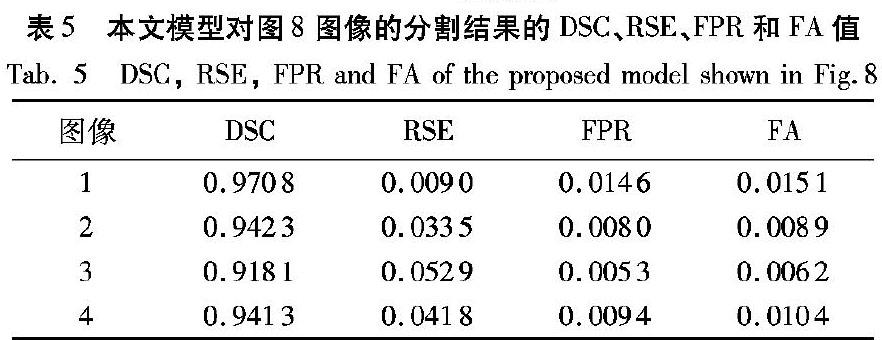
图8选取了4幅皮肤损伤图像对本文模型进行定量化评价。实验图像均来自于https：//isic-archive.com/api/v1，包含原始图像和对应的Ground Truth（GT图像）。

评价指标分别为Dice相似系数（Dice Similarity Coefficient， DSC）[17]，错误率（Ratio of Segmentation Error， RSE）[18]，假阳性率（False Positive Ratio， FPR）[19]和虚警率（False Alarm， FA）[20]。图8和表5的结果验证了本文模型的分割结果在客观上是较为准确的。本实验的初始轮廓均选取位于图像中心，边长400像素的正方形，迭代次数为500次。

3.6 应用举例

图9所示是本文模型分别对两幅红外图像（206×199、158×158），三幅医学图像（115×231、195×183、91×92）的分割结果。从图中可以看到，本文模型都取得了令人满意的结果。表6是对应的迭代次数和CPU时间。

4 结语

本文利用图像的全局信息和局部信息的极差定义了一个新的图像局部对比度，并以此定义了全局能量和局部能量的自适应权值，进而提出了一个自适应灰度拟合活动轮廓模型。所提模型不仅能够有效地分割灰度不均图像，而且与RSF模型、LGIF模型和LSACM模型相比，对初始轮廓的位置、大小和形状具有更强的鲁棒性。

参考文献

[1]CHEN B， HUANG S， LIANG Z R， et al. A fractional order derivative based active contour model for inhomogeneous image segmentation [J]. Applied Mathematical Modelling， 2019， 65： 120-136.

[2]陈星，王艳，吴漩.结合全局信息的局部图像灰度拟合模型[J].计算机应用，2018，38（12）：3574-3579.（CHEN X， WANG Y， WU X. Local image intensity fitting model combining global image information [J]. Journal of Computer Applications， 2018， 38（12）： 3574-3579.）

[3]李鋼，李海芳，尚方信，等.结合局部灰度差异的噪声图像分割模型[J].计算机应用，2018，38（3）：842-847.（LI G， LI H F， SHANG F X， et al. Noise image segmentation model with local intensity difference [J]. Journal of Computer Applications， 2018， 38（3）： 842-847.）

[4]CAI Q， LIU H Y， ZHOU S， et al. An adaptive-scale active contour model for inhomogeneous image segmentation and bias field estimation [J]. Pattern Recognition， 2018， 82： 79-93.

[5]韩斌，吴一全，宋昱.利用区域信息融合混合活动轮廓模型的河流遥感图像分割[J].中国图象图形学报，2017，22（2）：212-224. （HAN B， WU Y Q， SONG Y. Segmentation of remote sensing images of rivers utilizing a hybrid active contour model with regional information fusion [J]. Journal of Image and Graphics， 2017， 22（2）： 212-224.）

[6]CHAN T F， VESE L A. Active contours without edges [J]. IEEE Transactions on Image Processing， 2001， 10（2）： 266-277.

[7]LI C， KAO C-Y， GORE J C， et al. Implicit active contours driven by local binary fitting energy [C]// Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition. Piscataway， NJ： IEEE， 2007： 1-7.

[8]LI C， KAO C-Y， GORE J C， et al. Minimization of region-scalable fitting energy for image segmentation [J]. IEEE Transactions on Image Processing， 2008， 17（10）： 1940-1949.

[9]HE C J， WANG Y， CHEN Q. Active contours driven by weighted region-scalable fitting energy based on local entropy [J]. Signal Processing， 2012， 92（2）： 587-600.

[10]WANG L， LI C M， SUN Q S， et al. Active contours driven by local and global intensity fitting energy with application to brain MR image segmentation [J]. Computerized Medical Imaging and Graphics， 2009， 33（7）： 520-531.

[11]ZHANG K H， ZHANG L， LAM K M， et al. A level set approach to image segmentation with intensity inhomogeneity [J]. IEEE Transactions on Cybernetics， 2016， 46（2）： 546-557.

[12]蔡青，劉慧英，周三平，等.基于局部和全局信息的自适应水平集图像分割[J].强激光与粒子束，2017，29（2）：28-35.（CAI Q， LIU H Y， ZHOU S P， et al. Adaptive level set model based on local and global intensity information for image segmentation [J]. High Power Laser and Particle Beams， 2017， 29（2）： 28-35.）

[13]赵怡，邓红霞，张玲，等.基于最大类间方差的权重自适应活动轮廓模型[J].计算机工程与设计，2018，39（2）：486-491.（ZHAO Y， DENG H X， ZHANG L， et al. Weight-self adjustment active contour model based on method of maximum classes square error [J]. Computer Engineering and Design， 2018， 39（2）： 486-491.）

[14]ZHANG K H， SONG H H， ZHANG L. Active contours driven by local image fitting energy [J]. Pattern Recognition， 2010， 43（4）： 1199-1206.

[15]YU Y， ZHANG C M， WEI Y， et al. Active contour method combining local fitting energy and global fitting energy dynamically [C]// Proceedings of the 2010 International Conference of Medical Biometrics， LNCS 6165. Berlin： Springer， 2010： 163-172.

[16]LI C M， XU C Y， GUI C F， et al. Level set evolution without re-initialization： a new variational formulation [C]// Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Washington， DC： IEEE Computer Society， 2005， 1： 430-436.

[17]SHATTUCK D W， SANDOR-LEAHY S R， SCHAPER K A， et al. Magnetic resonance image tissue classification using a partial volume model [J]. NeuroImage， 2001， 13（5）： 856-876.

[18]LIU B， CHENG H D， HUANG J H， et al. Probability density difference-based active contour for ultrasound image segmentation [J]. Pattern Recognition， 2010， 43（6）： 2028-2042.

[19]ANTONIO L， SALAZAR-LICEA， CARLOS J， et al. Location of mammograms ROIs and reduction of false-positive [J]. Computer Methods and Programs in Biomedicine， 2017， 143： 97-111.

[20]LIU T Y， LO K T， ZHANG X D， et al. A new cut detection algorithm with constant false-alarm ratio for video segmentation [J]. Journal of Visual Communication and Image Representation， 2004， 15（2）： 132-144.

This work is partially supported by the Science and Technology Research Program of Chongqing Municipal Education Commission （KJQN201800537）， the National Fund Pre-research Project of Chongqing Normal University （16XYY21， 16XYY23）， the Doctor Start-up Foundation of Chongqing Normal University （17XLB001）.

ZHANG Xuyuan， born in 1993， M. S. candidate. His research interests include image processing based on partial differential equation.

WANG Yan， born in 1984， Ph. D.， associate professor. Her research interests include image processing based on partial differential equation.