耦合先验拉普拉斯坐标的半监督图像分割算法
曹昀炀 王涛


摘 要:针对传统半监督图像分割方法难以精确分割分散或细小区域的缺陷,提出了一种耦合标签先验和拉普拉斯坐标模型的半监督图像分割算法。首先,扩展拉普拉斯坐标(LC)模型,通过引入标签先验项进一步精确表征未标记像素点与已标记像素点之间的关系。然后,基于矩阵方程的求导优化,有效估计像素属于标签的后验概率,以实现图像目标分割的任务。得益于标签先验的引入,所提算法对分散或细小区域的分割更加鲁棒。最后,在多个公开的半监督分割数据集上实验结果表明,相比拉普拉斯坐标算法,所提算法的分割准确率获得了显著提升,验证了所提算法的有效性。
关键词:图像分割;彩色图像;半监督图像分割;拉普拉斯坐标;先验概率
中图分类号:TP391.413
文献标志码:A
Semi-supervised image segmentation based on prior Laplacian coordinates
CAO Yunyang1, WANG Tao2*
1.School of Statistics, East China Normal University, Shanghai 200241, China;
2.College of Computer Science and Engineering, Nanjing University of Science and Technology, Nanjing Jiangsu 210094, China
Abstract:
Focusing on the issue that classic semi-supervised image segmentation methods have difficulty in accurately segmenting scattered or small regions, a semi-supervised segmentation algorithm based on label prior and Laplacian Coordinates (LC) was proposed. Firstly, the Laplacian coordinates model was extended, and further the relationship between unlabeled pixels and labeled pixels accurately characterized by introducing the label prior. Secondly, based on the derivation of matrix equation, the posterior probability that the pixel belongs to the label was able to be effectively estimated, thus achieving the segmentation of the image. Thanks to the introduction of the label prior, the algorithm was more robust to the segmentation of scattered and small regions. Lastly, the experimental results on several public semi-supervised segmentation datasets show that the segmentation accuracy of the proposed algorithm is significantly improved compared with that of the Laplacian coordinates algorithm, which verifies the effectiveness of the proposed algorithm.
Key words:
image segmentation; color image; semi-supervised image segmentation; Laplacian Coordinates (LC); prior probability
0 引言
圖像分割是指在特定的相似性准则下将用户感兴趣的图像目标从复杂的背景环境中分离出来[1]。图像分割是从图像处理到图像分析的关键步骤,分割出的图像目标具有高维语义性,是后续图像应用的基础[2]。按照标签先验的获取方式,现有的图像分割方法一般可以分为三类:无监督方法[3-4]、半监督方法[5]和全监督方法[6]。无监督图像分割方法基于预先设定的相似性准则对图像特征进行聚类分析,可以实现自动的图像分割。然而,此类方法由于缺乏足够的用户先验指导,往往缺乏通用性与准确性。全监督图像分割方法基于全标记的图像样本序列进行模型参数训练,可以实现图像的语义层分割。典型的此类方法包括当下流行的卷积神经网络方法等[7]。此类方法的分割性能一般依赖于足够多的训练样本数据。此外,当出现训练样本中未包含的新类别时,往往无法获得正确的目标分割,导致此类方法缺乏一定的灵活性。半监督图像分割方法允许用户提供初始种子点或目标轮廓来表征标签先验信息,可以获得满足用户需求的分割结果。用户可以通过简单的人机交互方式,实现对分割过程的控制和对错误分割的有效修正,因此,半监督分割模式具有更强的通用性和灵活性。本文主要集中于半监督的分割模式展开研究工作。
近年来,大量的半监督分割方法[8-14]被提出。典型的方法包括图割(Graph Cut, GC)[8]和随机游走(Random Walk,RW)[9]。在上述方法中,用户需要首先标记一些像素点作为种子点,然后算法可以基于种子点自动地估计未标记像素点的标签。Boykov等[8]首次提出了半监督图割算法,并应用于医学图像分割中,利用像素之间的相似程度定义能量,将能量函数定义为区域能量和边界能量之和。该算法添加了两个虚拟的终端点,用区域能量衡量像素点和终端点之间的相似程
度,边界能量衡量相邻像素点之间的相似程度,将图像分割问题转化为求取图的最小割集问题,通过最大流算法获取全局的最优解。但是传统的图割算法是在统计直方图的基础上,由于直方图的局限性,图割算法较难准确地分割包含复杂背景的图像。Grady[9]提出随机游走算法,通过构建从未标记像素点出发到种子点终止的随机游走模型,求解带有边界约束的Dirichlet问题,估计出每一个未标记像素点到种子点的到达概率。将未标记的像素点与其到达概率最大的种子点合并为目标区域。传统的随机游走算法完全依赖种子点的质量和位置,因此当种子点较少时,该算法的分割结果错误率较高。此外,随机游走算法忽视了标签的各向异性传播,对区域边界不敏感,容易出现边界拟合较差的问题。针对这些问题,Casaca等[10]提出结合拉普拉斯坐标(Laplacian_Coordinates,LC)的半监督图像分割算法改进随机游走模型。该算法对每个像素点赋值,求出最小化能量函数的最优解,之后将最优解转化为像素点属于前景或背景的概率,将像素点与其概率最大的标签合并为目标区域。相比于传统的随机游走算法最小化相邻像素点之间的距离的做法,拉普拉斯坐标算法通过最小化所有相邻像素点距离的均值来更好地控制标签的各向异性传播,同时也提高了边界拟合的准确性。此外,拉普拉斯坐标算法的能量函数包含二次型矩阵,能够降低计算成本,并确保分割结果的准确性和平滑性。但是由于忽视未标记像素点与种子点之间的特征,只依赖相邻像素点的特征,拉普拉斯坐标算法仍难以分割出分散或细小的区域。此外,近些年来为了提升随机游走模型的分割准确度,Bampis等[11]提出归一化随机游走(Normalized Random Walk, NRW)算法;Dong等[12]提出亚马尔可夫随机游走(Sub-Markov Random Walk, SMRW)算法。但是归一化随机游走算法仍难以分割出分散或细小的区域,亚马尔可夫随机游走算法会存在过度分割的问题。
受现有标签先验建模方法[8,15-18]的启发,本文基于拉普拉斯坐标模型[10]提出了一种半监督图像分割算法,针对拉普拉斯坐标算法难以分割分散或细小区域等缺陷,通过引入标签先验来精确表征未标记像素点与种子点之间的关系。在传统拉普拉斯坐标模型能量项中引入标签先验概率项,并有效优化各能量项之间的参数,充分利用用户交互知识,弥补传统模型的缺陷。本文提出的耦合先验拉普拉斯坐标的半监督图像分割算法从以下两个方面提升了图像分割性能:1)在分割过程中引入先验概率,对分散或细小的区域更鲁棒;2)通过合理优化参数,平衡各项约束的影响,在分割小目标区域的同时保持分割区域的边界更平滑。
1 相关研究
图像可以用图G=(P,W)来表示,其中P={pi}Ni=1为所有像素点的集合,W=[Wij]N×N为像素之间的相似性矩阵,Wij∈[0,1]表示像素pi和pj之间的相似性,N为像素点的个数。图像分割问题实质是标签划分问题,即给定一个标签集合L,一个图像像素集合P,图像分割的目标是给每一个像素点pi∈P赋予对应的标签值li∈L。因此图像的分割结果即为从图像像素集合P到标签集合L的一组映射,表示为l={li|li∈L}。前景和背景的半监督图像分割问题可以看作是二值标签问题,即L={lF,lB},其中lF代表前景的标签值,lB代表背景的标签值,一般赋值为lF=1,lB=0。
1.1 图割算法
基于图割的图像分割算法将标签划分问题转化为能量函数最小化的问题。能量函数一般可以表示为:
E(l)= Er(l)+ λEb(l)(1)
其中:能量函数E (l)由区域能量项Er和边界能量项Eb组成。λ>0为平衡区域项和边界项的参数。该能量函數可以采用最大流/最小割算法来优化,有效地寻找图中的最小割集,从而获得全局最优解。其中,区域能量项表示像素点和标签之间的相似程度,是关于种子点属于前景或背景的概率的函数。文献[19]提出了使用高斯混合模型(Gaussian Mixture Model, GMM)估计像素点属于前景和背景的概率的方法,基于GMM的区域能量项定义如下:
Er(l)=∑Ni=1(-ln(PGMM(Ci,li)))(2)
其中:PGMM(Ci,li)表示像素点pi属于标签li的概率。Ci表示像素点pi的特征强度向量,对于彩色图像分割,用RGB特征定义像素点pi的特征强度向量Ci=(Ri,Gi,Bi);对于灰度图像分割,用灰度值代表像素点pi的特征强度向量Ci。
图割算法在分割背景环境较为简单的图像时一般能获得较好的结果,当图像的背景环境较为复杂时,容易出现分割速度缓慢,错误分割小区域目标等缺陷,导致分割结果不够精确和鲁棒。
1.2 随机游走算法
基于随机游走的图像分割算法是另一种实用的半监督图像分割算法。该算法基于随机游走者从每个未标记像素点到种子点的转移概率,定义未标记像素点属于种子点对应标签的概率。在基于随机游走的图像分割算法中,通常用高斯函数定义像素pi和pj之间的相似性Wij,表达式如下:
Wij=exp(-β‖Ci-Cj‖2), pj∈Ai
0,其他(3)
其中:Ci表示像素pi的特征强度向量,Ai表示像素pi的邻域像素集合, β为控制参数。进而可以根据像素属于标签l∈{lF,lB}的概率构造能量函数,表达式如下:
E(πl)=12∑Ni, j=1Wij(πil-πjl)2=12πTlLπl(4)
其中,πl=[πil]N×1为像素属于标签l的概率向量,πil为像素pi属于标签l的概率。L=D-W为拉普拉斯矩阵,其中D=diag(d1,d2,…,dN),di=∑Nj=1Wij,W=[Wij]N×N。为了降低计算复杂度,可以将拉普拉斯矩阵转变为分块矩阵,仅计算未标记的像素属于标签l的概率。将像素集合P划分为标记的像素集合PM和未标记的像素集合PU满足PM∩PU=,PM∪PU=P。因此未标记像素属于标签l的概率向量表达式如下:
li=1, πi≥0.5
0,πi<0.5(13)
对于多目标分割问题,需要分别计算所有像素属于各个标签的后验概率向量,其后验概率计算公式为前景和背景分割计算公式的高维推广,表达式如下:
πq=(K+L2)-1KYq(14)
其中:πq=[πiq]N×1表示所有像素属于标签lq的后验概率向量,Yq=[yiq]N×1表示所有像素属于标签lq先验概率向量,当pi为未标记像素时,yiq=iq=PGMM(Ci,lq),当pi为属于标签lq的种子点时,yiq=1,当pi为不属于标签lq的种子点时,yiq=0。q=1,2,…,n,n为标签总数。矩阵K和L的含义保持不变。最后,将像素分配给后验概率最大的标签。
与现有的半监督图像分割算法相比,本文算法增加了标签先验项,利用了种子点与未标记像素的特征关系,在保证标签各向异性传播的同时,使得分割结果对分散或细小的区域更加敏感。
3 实验与结果分析
本文实验选用的图像来自于MSRC数据集[19]、Graz数据集[20]和LHI数据集[21]。MSRC、Graz、LHI数据集提供了用户交互信息和正确分割结果,是评价半监督图像分割方法最常用的数据集。本文选用错误率、重叠度(Intersection over Union, IoU)和运行时间作为评价分割结果的定量指标。错误率的定义如下:
错误率=错分类像素点数未标记像素点数(15)
其中,错分类像素点和未标记像素点均不包括种子点。IoU是分割问题中常用的标准性能度量指标,表示估计结果与真实结果的重叠度,IoU值越大表示分割效果越好。本文实验基于英特尔酷睿I5 CPU以2.0GHz的频率在Matlab进行,在同等情况下测算运行时间。本文算法将与一系列随机游走算法进行比较实验,包括随机游走(RW)算法、拉普拉斯坐标(LC)算法、归一化随机游走(NRW)算法、亚马尔可夫随机游走(SMRW)算法。根据文献[10],LC算法的控制参数k1、k2、k3均设为1;本文算法的常数m设为105,控制参数k设为10-7。
3.1 定性比较
本文根据分割结果的可视化对4种经典算法和本文算法进行定性评估。图1所示为5种算法的分割结果。
图1(b)表示种子点信息,白色的像素被标记为前景种子点,黑色的像素被标记为背景种子点,其余为未标记像素。本文基于未标记像素点的分割错误率比较分割结果。从图中可以看出,由于忽视了标签传播的各向异性,RW算法和NRW算法对细小和分散的区域不敏感。由于依赖相邻像素点之间特征强度的关系,在相邻像素点之间特征强度相差较大时,LC算法容易停止分割,从而导致错误分割边界。SMRW算法对细小区域过于敏感,分割出的边界很不平滑。本文算法改善了已有随机游走算法的缺陷,对分散或细小的目标更加敏感,获得了较好的分割结果。以第一幅图“cross”为例,十字架与立柱连接处的像素颜色特征与其邻域内像素的颜色特征相差较大,因此传统算法仅以连接处为目标的边界。SMRW算法虽然正确分割出十字架,但是房屋边界的分割结果非常不平滑。然而,本文算法引入了标签先验信息,因为十字架的颜色特征与前景种子点的颜色特征非常接近,所以十字架被分割成前景目标。因此本文算法对分散的目标更加敏感。以第二幅图“sheep”为例,由于绵羊腿部颜色与身体颜色相差较大,并且羊腿与身体距离较远,因此RW算法和NRW算法无法分割出羊腿。LC算法虽然考虑了标签的各项异性传播,能够分割出部分羊腿,但是由于羊腿区域细长并且颜色特征与邻域内像素的颜色特征相差较大,因此LC算法仍无法分割出全部的羊腿。由于羊腿的颜色特征与前景标签中绵羊面部的颜色特征近似,所以本文算法分割羊腿的效果更好,因此本文算法对细小的目标更加敏感。
3.2 定量比较
本文在MSRC、Graz、LHI数据集上对5种算法作定量评估,以分割的平均错误率、平均IoU和平均运行时间为评估指标。对于MSRC数据集上的50幅测试图像,RW算法的平均错误率为7.46%,LC算法的平均错误率为5.06%,NRW算法的平均错误率为5.92%,SMRW算法的平均错误率为4.62%,本文算法的平均错误率为4.02%。可以看出本文算法的错误率相对于RW算法和LC算法具有显著下降,并明显优于近年来提出的NRW算法和SMRW算法。表1为在三种数据集上五种算法的平均IoU和平均运行时间,可以看出本文算法的平均IoU约为0.85,在各个数据集上明显高于其余四种算法,分割结果更准确。同时,本文算法每幅图的平均运行时间约3.1s,明显快于近年来提出的NRW算法和SMRW算法。因此,本文算法引入标签先验项,能够进一步提升拉普拉斯坐标的算法分割的准确度,提升运算速度,具有可行性。
图2为5种算法在MSRC数据集50幅测试图像的分割错误率的比较,其中图像ID根据本文算法的错误率由低到高排序,可以看出本文算法在大部分测试图像中获得了最优的结果。表2为本文算法在MSRC数据集50幅测试图像上的分割错误率。
3.3 多目标分割
对于多目标分割问题,本文选取2幅测试图像的分割结果,定性分析本文算法的准确度。图3为多目标分割结果,测试图像的种子点需要用戶手动地标记。如图3(a)所示,红色、绿色和蓝色的像素分别表示三种不同标签的种子点。如图3(b)所示,在多目标分割中,本文算法分割结果仍比较准确,并且对细小的目标敏感。以第一幅图“201080”为例,尽管种子点没有直接标记建筑物顶端的装饰,但是本文算法仍将细小的装饰正确分割,从而验证了在多目标分割问题中本文算法的有效性和可行性。
4 参数设置
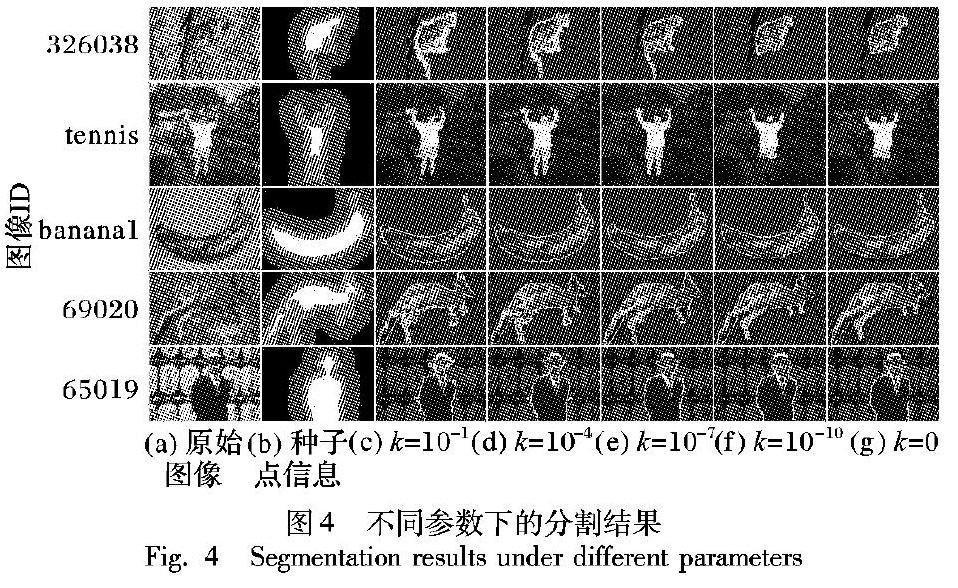
本文通过设定合适的参数k来控制标签先验项的约束强度。图4为不同参数k下的分割结果。由图可以看出,当参数较大时,如图4(c)和(d)所示k=10-1,k=10-4时,过度考虑了未标记像素点与种子点之间的特征强度关系,导致分割结果中出现杂质点、目标区域不连通等缺陷。当参数较小时,如图4(f)和(g)所示k=10-10,k=0时,标签先验项作用不明显,分割结果更接近于拉普拉斯坐标算法的结果,容易错误分割细长的区域。当k=10-7时,本文算法在50幅测试图像上得到了较好的分割结果。为了更精确地比较不同参数下的分割精度,本文选用平均错误率定量评估。表3为不同参数下分割结果的平均错误率。可以看出在k=10-7时,平均错误率最小,分割精度最高。因此本文选择控制参数k=10-7。
5 結语
本文在传统的拉普拉斯坐标算法中引入标签先验项,考虑了未标记像素点和种子点之间的特征强度关系,构造了含有二次型矩阵的能量函数,通过求解能量函数的最小值获得像素属于标签的后验概率,然后根据后验概率分割区域。本文解决了经典算法中分割结果不平滑、错误分割细小和分散的目标区域的问题。为了提高分割的精度,本文通过设置合适的控制参数平衡各项约束的影响,在分割出小目标区域的同时使分割区域的边界更平滑。最后通过对比实验以及在数据集上的定性和定量评估证实了本文算法的实用性和通用性。本文算法仍存在一些缺陷,如种子点较少时分割精度较低、控制参数需要凭经验手动设定等。如何根据不同的图像环境设定参数值,将是今后的研究工作。
参考文献
[1]SONKA M, HLAVAC V, BOYLE R. Image Processing, Analysis and Machine Vision [M]. Berlin: Springer, 2003: 175-176.
[2]XIA G, SUN H, FENG L, et al. Human motion segmentation via robust kernel sparse subspace clustering [J]. IEEE Transactions on Image Processing, 2018, 27(1): 135-150.
[3]JI Z, XIA Y, CHEN Q, et al. Fuzzy c-means clustering with weighted image patch for image segmentation [J]. Applied Soft Computing, 2012, 12(6): 1659-1667.
[4]JI Z, XIA Y, SUN Q, et al. Fuzzy local Gaussian mixture model for brain MR image segmentation [J]. IEEE Transactions on Information Technology in Biomedicine, 2012, 16(3): 339-347.
[5]WANG T, JI Z, SUN Q, et al. Label propagation and higher-order constraint-based segmentation of fluid-associated regions in retinal SD-OCT images [J]. Information Sciences, 2016, 358(C): 92-111.
[6]KUNTIMAD G, RANGANATH H S. Perfect image segmentation using pulse coupled neural networks [J]. IEEE Transactions on Neural Networks, 1999, 10(3): 591-598.
[7]SHELHAMER E, LONG J, DARRELL T. Fully convolutional networks for semantic segmentation [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017, 39(4): 640-651.
[8]BOYKOV Y Y, JOLLY M. Interactive graph cuts for optimal boundary and region segmentation of objects in N-D images [C]// Proceedings of the 8th IEEE International Conference on Computer Vision. Piscataway, NJ: IEEE, 2001: 105-112.
[9]GRADY L. Random walks for image segmentation [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2006, 28(11): 1768-1783.
[10]CASACA W, NONATO L G, TAUBIN G. Laplacian coordinates for seeded image segmentation [C]// Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 2014: 384-391.
[11]BAMPIS C G, MARAGOS P, BOVIK A C. Graph-driven diffusion and random walk schemes for image segmentation [J]. IEEE Transactions on Image Processing, 2017: 26(1): 35-50.
[12]DONG X, SHEN J, SHAO L, et al. Sub-Markov random walk for image segmentation [J]. IEEE Transactions on Image Processing, 2016, 25(2): 516-527.
[13]HEIMOWITZ A, KELLER Y. Image segmentation via probabilistic graph matching [J]. IEEE Transactions on Image Processing, 2016, 25(10): 4743-4752.
[14]JIAN M, JUNG C. Interactive image segmentation using adaptive constraint propagation [J]. IEEE Transactions on Image Processing, 2016, 25(3): 1301-1311.
[15]ZEMENE E, PELILLO M. Interactive image segmentation using constrained dominant sets [C]// Proceedings of the 2016 European Conference on Computer Vision, LNCS 9912. Berlin: Springer, 2016: 278-294.
[16]WANG T, SUN Q, JI Z, et al. Multi-layer graph constraints for interactive image segmentation via game theory [J]. Pattern Recognition, 2016, 55(C): 28-44.
[17]BAI S, BAI X, TIAN Q, et al. Regularized diffusion process for visual retrieval [C]// Proceedings of the 31st AAAI Conference on Artificial Intelligence. Palo Alto: AAAI Press, 2017: 3967-3973.
[18]WANG T, YANG J, JI Z, et al. Probabilistic diffusion for interactive image segmentation [J]. IEEE Transactions on Image Processing, 2019, 28(1): 330-342.
[19]ROTHER C, KOLMOGOROV V, BLAKE A. Grabcut: interactive foreground extraction using iterated graph cuts [C]// Proceedings of the 2004 ACM SIGGRAPH Conference. New York: ACM, 2004: 309-314.
[20]SANTNER J, POCK T, BISCHOF H. Interactive multi-label segmentation [C]// Proceedings of the 2010 Asian Conference on Computer Vision, LNCS 6492. Berlin: Springer, 2010: 397-410.
[21]YAO B, YANG X, ZHU S. Introduction to a large-scale general purpose ground truth database: methodology, annotation tool and benchmarks [C]// Proceedings of the 2007 International Workshop on Energy Minimization Methods in Computer Vision and Pattern Recognition, LNCS 4679. Berlin: Springer, 2007: 169-183.
[22]王濤.特征度量与信息传递的交互式图论分割方法研究[D].南京:南京理工大学,2017:17-29. (WANG T. Research on graph theory based interactive segmentation via feature measurement and information propagation [D]. Nanjing: Nanjing University of Science and Technology, 2017: 17-29.)
This work is partially supported by the National Natural Science Foundation of China (61802188), the Natural Science Foundation of Jiangsu Province (BK20180458), the Jiangsu Planned Project for Postdoctoral Research Fund.
CAO Yunyang, born in 1998. His research interests include applied statistics, image segmentation.
WANG Tao, born in 1990, Ph. D., associate professor. His research interests include computer vision, image segmentation.

