指向核心素养的数学教学

李文会

摘 要 随着2016年9月13日《中国学生发展核心素养》的发布，2017版《普通高中数学课程标准》明确将“数学学科核心素养”定义为：“具有数学基本特征的思维品质、关键能力以及情感、态度和价值观的综合体现，是在数学学习和应用过程中逐步形成和发展的。”同时提出了数学抽象、逻辑推理、数学建模、数学运算、直观想象和数据分析这六大数学学科核心素养。

关键词 小学数学 核心素养 比例

中图分类号：G633文献标识码：A

1基于《比例的意义》一课浅谈数学建模一般性结果的人文温度

在人教版小学数学教材中，《比例的意义》一课本安排在六年级下册第四单元的第一课时，属于典型的概念或意义建构类的内容，其是同一单元后续如《比例的基本性质》、《正比例和反比例》和《图形的放大和缩小》等相关内容教学的重要基础：（ 见教材：六年级下册《比例的意义》）

从具体情境来看，为强化“两个比相等”对于組成比例的决定性作用。教材的书面性引导语更为聚焦对大小不同但形状相同的国旗的长和宽的比值上，通过借助相应数据计算比值的方式实现对“两个比相等”的内在感悟，进而顺理成章用“=”表达相应的相等关系。

在本节课的教学实践中，当学生根据给出的数据验证任意两面国旗长和宽的比值相等，并形成对比例的意义的初步感悟后，教师给了学生自主质疑的时间和空间。而正中下怀的“反馈”如期而至：“是不是比值相等，比就相等？”而所有学生在第一时间用一个“是”字对这样的质疑做出了回应。这样的局面不应简单归咎于学生的不假思索，要知道对于万事万物，“意义”永远无法脱离生活而独立存在，即使是在上述第一次抽象已经完成的情况下。很显然教材文本对比值过强的指向性让学生对比例意义的数学思考没有了温度，在学生心中，“比例”已经彻底沦为了满足某种游戏规则的“四个数的产物”。

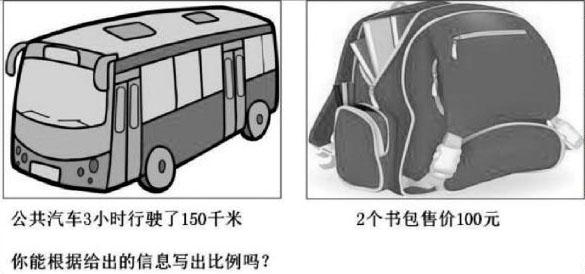
面对学生这种具有高度趋同性的预设范围内的生成，本人迅速做出反应，出示了如下的问题情境：

面对情境，学生运用自身多年训练形成的运算能力直奔比值而去。并在短短几秒钟基于相等的比值迅速给出了“150：3=100：2”的结果。很显然，情境对于理解“意义”的不可或缺在学生心里已经不再重要，这再一次佐证了学生在新知的理解与把握方面温度的缺失。在等待了良久之后，终于有学生开始将50千米/时的平均速度和50元/个的单价还原到生活中去，并引领全体学生对比例中两个比的等价关系进行质疑。因理解能力和认知水平存在个体差异，学生对“比例的意义”的重新诠释和观念的转变并不同步，但最终大多数学生对“比值相等是比相等的必要而不充分条件”的结论达成了共识，即比值相等比不一定相等，而比相等比值一定相等。虽然温度的回升让习得的结果重新具有了人文的属性，但即使是这样，依然有部分学生不愿进行自我否定而固守自己的“阵地”。那么如此程度根深蒂固的影响来自何方呢？让我们顺藤摸瓜、溯本求源，结合教材内容去寻找真因。

2比例、比、分数和除法在意义建构上的一脉相承

人教版六年级上册《比的意义》（见教材）的内容，图中的内容“两个数的比表示两个数相除”。 “比”能够执行除法的运算是不争的事实，但“意义”往往体现在结果上，仅仅将“比”视为一种运算同样是失去温度的表现。当过分从“数”的角度关注比值大小而不去从“数量”的角度去理解第三种数量的意义时，出现上述《比例的意义》一课的局面也就不足为奇了。

把一根2m长的木条锯成同样长的4段，每段是这根木条的，每段长（  ）？  ）=（  ）m=m。

接下来，让我们继续来看与“比”息息相关的更早出现的“分数”：

题为人教版五年级下册考查《分数的意义》一个内容的常见命题，学生常常将结果填反，即第一问算“2？”的结果，第二问算“1？”的结果。究其根本原因，是对与上述“比”的两种不同意义相对应的“分数”的两种不同意义的理解缺乏清晰的认识。第一问与其说是1段和4段的关系，不如说是“0.5m”和“2m”的关系，其本质是上述同类量的比，因此得到的结果是不含名称表示关系的分数，第二问实际上是“2m”和“4段”之间的关系，其本质是上述不同类量的比，因此得到的结果是第三种数量，如果这一问的最终结果配以“米/段”的名称，是完全可行的。

从上面的论述中我们体会到，对“比”的意义两种不同的理解并不是无中生有的空穴来风，实则在教学《分数的意义》时已然发生，《比的意义》的教学实际上是对两种不同理解的拓展和延伸。这再一次说明站在全套教材至高点处对教学内容的纵向整体把握、以认知发展的角度紧扣前后之间联系的必不可少。

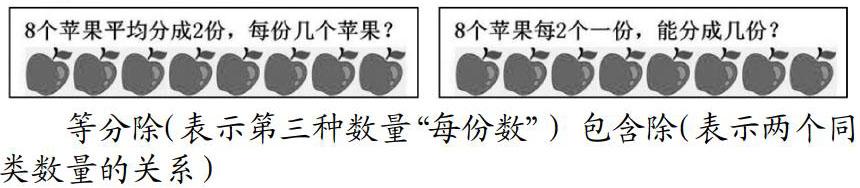
如果从分数产生于“平均分”过程的角度去理解，我们不难想到“除法”为分数的前身，但这样的理解仅仅涉及了分数的意义中的一则，即与“平均分”相对应的表示第三种数量的带名称的分数的意义。实际上除法有“包含”和“等分”两种基本的类型，这其实就是与分数的意义以及比的意义相对应的除法的两种不同的意义：

等分除（表示第三种数量“每份数”）   包含除（表示两个同类数量的关系）

通过以上比例、比、分数和除法在意义建构上的对比分析，我们不难感受到一脉相承的意味深长。如果重新来过，这些相互关联的同一支路上的内容将会是训练和培养学生自主迁移和类比探究能力的良好素材，将促使学生实现对共同本质更好地理性把握。但这一切都要以将生活作为“意义”的载体为前提，否则，学生只是在“数”的世界中进行没有温度的纵向深入，也是与发展数学学科核心素养的初衷背道而驰的。

参考文献

[1] 史宁中.数学基本思想18讲[M].北京：北京师范大学出版社，2016：22-27.