一种城轨列车的混合动力能量优化控制

石 岩,高锋阳,2,张国恒,强国栋,高云波

(1.兰州交通大学自动化与电气工程学院,兰州 730070； 2.甘肃省轨道交通电气自动化工程实验室(兰州交通大学),兰州 730070)

引言

传统的城轨车辆供电方式大多采用接触网供电和地面接触轨供电。相对于现有无接触网式有轨电车而言,燃料电池混合动力有轨电车自身配备发电系统,不依赖于外部牵引供电系统,可以实现全程无网运行,并且环保无污染,在轨道交通领域有着巨大的应用前景。近年来,基于质子交换膜燃料电池(proton exchange membrane fuel cell, PEMFC)的混合动力机车由于清洁、环保、能量利用率高,引起了国内外对混合动力机车的研发热潮[1-3]。采用混合动力供电的城轨列车,其主要动力源是燃料电池,超级电容和锂电池作为能源辅助系统和存储系统。锂电池在机车启动和加速时辅助燃料电池,并吸收再生制动时产生的能量,而超级电容则表现出最快的动态响应,主要是对功率实现“削峰填谷”。在燃料电池和锂电池的输出侧串联DC/DC变换器,从而根据负载功率需求调整各动力源输出功率[4-6]。

燃料电池、锂电池和超级电容之间的能量分配取决于能量管理策略。目前,能量管理控制策略有滤波器控制、粒子群算法控制、模糊逻辑控制、动态规划算法控制和功率跟随控制法等[7]。滤波器控制通常采用低通滤波器,滤波效果特别好,但它会给控制系统带来不稳定,不能较好地适应多变的实际工况[8]。粒子群算法控制是从随机解出发,通过迭代寻找最优解,易陷于局部最优解,并且导致收敛精度低[9]。模糊逻辑控制是基于规则的控制策略,主要简化系统设计的复杂性,适用于非线性、时变、模型不完全的系统[10]。模糊控制的缺点是控制精度有限,灵活度不足,不能及时地进行在线调整燃料电池、锂电池和超级电容之间的功率分配。以上规则控制策略主要用于燃料电池混合动力系统的初级能量管理,在实际应用中易于实现,但是规则很难改变,并且没有充分考虑能量系统是否工作在最优能耗状态[11]。文献[12]应用动态规划来解决混合动力电动卡车的最小燃料优化控制问题,开发了针对驾驶循环的能量管理问题的动态最优解决方案,但是其计算量特别繁重,而且动态编程算法产生的反馈定律是不能实现的。在基于能量优化管理控制策略方面,有学者采用功率跟随控制法对燃料电池机车进行控制,在满足机车功率需求的同时,可以让锂电池等辅助供电设备工作在最优状态,但无法对系统进行有效的保护[5]。

基于以上的分析,提出基于等效氢耗的能量管理策略。主要求解等效氢耗优化问题,计算出最佳的燃料电池功率,最大限度地减少混合动力车的氢气消耗。与基于经典PI控制策略进行对比,等效氢耗最小的控制策略在控制周期内,使得能量系统工作在最优能耗状态[13]。

1 混合动力系统设计

由于燃料电池动态响应速度慢,并且无法满足瞬时高功率需求,故采用混合动力系统供电。为了使混合动力系统的能量稳定输出,且保持母线电压稳定,设计了一种多个供电模块并联输出的供电模型。并联式混合供电系统结构如图1所示。

图1 混合动力系统结构框图

混合供电系统将超级电容、锂电池的荷电状态水平及燃料电池的实时输出功率反馈至能量管理控制器,能量管理控制器通过控制DC/DC变换器,稳定母线电压并对各供电模块进行功率分配[14]。

1.1 燃料电池系统模型

燃料电池系统模型采用氢氧燃料电池电堆模型[15],燃料电池的模型如图2所示,模型的数学表达式如下

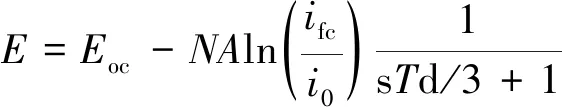
(1)

Vfc=E-Rohm·ifc

(2)

式中,E为燃料电池的等效输出电压；Vfc为燃料电池电堆电压；ifc为燃料电池电堆输出电流；Eoc为燃料电池开路电压；N为电堆单节电池数目；A为塔菲尔斜率；Td、Rohm、i0分别为燃料电池响应时间、电堆内阻以及电池交换电流。

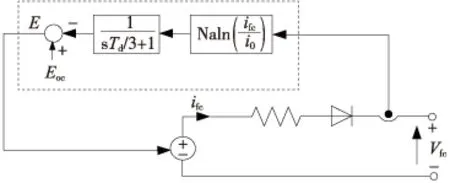
图2 燃料电池系统模型

1.2 锂电池模型

锂电池具有快充快放的特点,并且容易受到温度的影响,再加上在实际中锂电池荷电状态(State of Charge, SOC)不能直接测得其状况,使得建立可准确模拟电池工作特性的模型较为困难。为了更方便获得较为准确的SOC值,建立RC等效模型,如图3所示。

图3 锂电池系统模型

图3中,Ut为端电压；R0为欧姆内阻；Cc为电池的总容量；Ce为极化电容；Rc为电化学电阻；Re为极化电阻；Uoc和Ue分别为开路电压和极化电压。等效电路的输入、输出分别为电流I和端电压Ut,并规定充电时I为正,放电时I为负。

根据基尔霍夫定律,可以得到端电压的表达形式

Ut=Ue+IeRe+IR0

(3)

式中,Ic、Ie分别为RC支路上的电流。电路中电流的表达式为

I=Ic+Ie

(4)

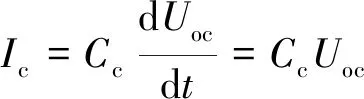
(5)

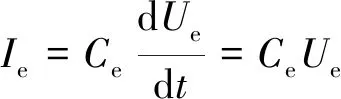
(6)

1.3 DC/DC变换器拓扑结构

燃料电池通过单向DC/DC变换器连接到直流母线上,使得PEMFC即使在负载功率频繁变化的情况下也可以稳定的输出能量,同时避免了高功率对PEMFC的冲击,从而起到了保护燃料电池的作用[11],拓扑结构如图4所示。

图4 单向DC/DC变换器拓扑结构

蓄电池通过双向DC/DC变换器与直流母线相连,在蓄电池放电时,进行升压操作；在蓄电池充电时,则进行降压操作。拓扑结构如图5所示。

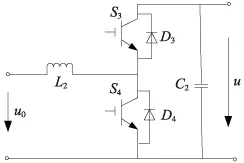
图5 双向DC/DC变换器拓扑结构

2 等效氢耗策略

等效氢耗策略(Equivalent consumption strategy, ECMS)是一种基于等效燃料消耗的瞬时优化策略。在燃料电池混合动力系统中,有氢能和电能两种能量。其中电能来自于锂电池,氢能来自于燃料电池。为了使不同混合动力系统的能量消耗具有可比性,引入等效氢耗量的概念,即将储能装置的电能消耗等效为相应的氢能消耗[13]。系统总的氢气消耗量C是由燃料电池氢气消耗量Cfc、锂电池与超级电容的等效氢耗Cbat和CSC组成的。该控制着重于计算最佳的燃料电池功率,最大限度地减少混合动力车的氢气消耗。系统的最小燃料消耗如下式所示

Pfc=min(Cfc+k1·Cbat+k2·CSC)

(7)

式中,Pfc为燃料电池输出功率；k1和k2为惩罚系数。

考虑到超级电容主要是对功率实现“削峰填谷”,与Cfc或Cbat相比其贡献将是最小的,因此,Csc可以忽略不计。因此式(7)可以改写如下

Pfc=min(Cfc+k1·Cbat)

(8)

由文献[16]中的静态工作曲线可知,Cfc和Pfc的关系可以由以下表达式近似表示

Cfc=c·Pfc2+b·Pfc+a

(9)

式中,a,b,c为拟合系数,仅取决于所选择的燃料电池。电池等效氢气消耗Cbat可以根据锂电池功率Pbat和电池的SOC获得。其中由于燃料电池的工作点不确定,故使用燃料电池的平均值进行计算,如下式所示

(10)

其中

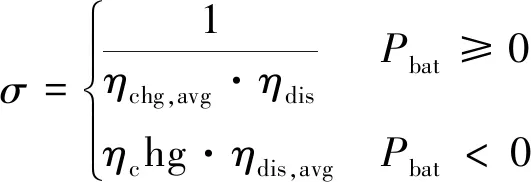
(11)

式中,CFC,avg为燃料电池的平均氢气消耗量；PFC,avg为燃料电池的平均功率；ηchg和ηdis分别为电池充电和放电的效率；ηchg,avg和ηdis,avg分别为锂电池的平均充放电效率。锂电池的效率可用下式表示

(12)

式中,Ebat为电池开路电压,Rchg和Rdis为电池充电和放电的阻力,假设电池充电和放电阻力等于电池内部电阻Ri。如文献[17]所述,惩罚系数k1可以表示为

(13)

常数μ可以准确地反映锂电池的充放电过程[18]。μ在列车运行期间可以平衡锂电池的SOC(在此选择μ=0.65)使得锂电池的SOC处在合理的范围内。其中,SOCL为SOC的下限,SOCH为SOC的上限。因为Csc与Cfc或Cbat相比被忽略了,方程式中使用的燃料电池功率可以计算如下

Pfc=Pm/ηm+Paux-Pbat

(14)

其中,Pm为电动机的输出功率；ηm为电动机的效率；Paux为燃料电池附件所消耗的功率。机车所需的总功率Pload计算如下

Pload=Pm/ηm+Paux

(15)

由以上推导可知最小化问题可以表述为

Pbat,opt=min(c(Pload-Pbat)2+b(Pload-Pbat)+a+

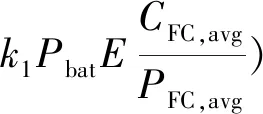
(16)

考虑到Pload和a可以被认为是最小化问题中的常数,故上式可表示如下

Pbat,opt=min(c(Pbat)2+

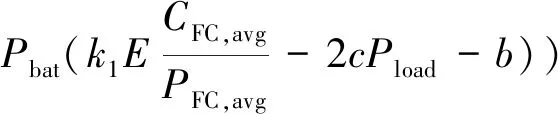
(17)

定义一个新的常数

(18)

方程式中所表达的问题的最优解

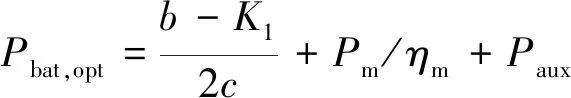
(19)

燃料电池的优化功率Pfc,opt可以通过计算得出

Pfc,opt=max(min(±Pm+Paux-Pbat,opt,Pfc,max),Pfc,min)

(20)

式中,Pfc,max为燃料电池的最大功率；Pfc,min为燃料电池的最小功率；±Pm为电动机的正负功率,文中使用可编程负载代替了负载电动机。

3 仿真分析

为了验证所提能量优化方法的有效性和准确性,在MATLAB/Simulink中搭建了燃料电池、锂电池和超级电容3种混合动力系统的仿真模型,锂电池SOC初始值为65%,仿真时间设置为350 s,系统参数如表1所示。

表1 系统仿真参数

3.1 功率分配对比

图6为在相同的条件下,采用经典PI控制策略和ECMS控制策略下的功率分配。在0～40 s时,列车未启动,燃料电池对辅助供电单元进行预充电,为列车启动做准备。40 s时列车启动,负载功率迅速增大,之后进入平稳运行阶段,在60 s时负载功率再次迅速增加,从60 s到140 s,列车进入高负载功率运行阶段,辅助供电单元同时提供能量以满足列车所需要的功率。在140 s到180 s之间,负载需求功率整体呈现减小的趋势,在 180 s时功率需求最小,为-3 kW,这一时期列车为制动阶段,列车回收能量,为辅助供电单元充电,之后列车进入高功率运行阶段,在240 s时再次进入制动状态,最后列车以低负载功率运行,330 s后负载需求功率开始减小直到为0,列车运行结束。图6(a)中锂电池作为辅助供电单元,当负载急剧上升时,锂电池可以提供较高的功率来辅助燃料电池进行供电,保证供电的可靠性,并且锂电池的输出功率更为平缓。图6(b)中当负载急剧变化时,在列车启动阶段锂电池没有起到辅助燃料电池供电的作用,并且锂电池输出波动较大。所以,采用ECMS控制策略可以充分利用辅助单元锂电池进行供电,并使得锂电池的输出更加平稳。

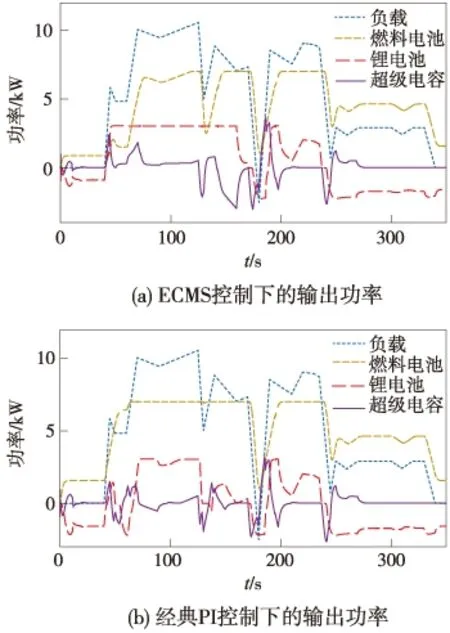
图6 两种控制策略下的功率分配对比

3.2 燃料消耗、锂电池SOC对比

通过图7(a)可以明显看到在PI控制下的锂电池的SOC从65%上升到65.8%,最低跌落到61.8%,ECMS控制下的电池的SOC从65%上升到65.8%,最低跌落到58%,在一个运行周期结束后,前者电池的SOC最终约为63%,后者电池的SOC最终约为59%。

这是因为在列车启动前期,PI控制策略下的锂电池没有起到辅助供电的作用,有一段时间在进行充电,所以剩余电量较多,但两种方法都能使得锂电池的SOC保持在合理的水平,说明了ECMS控制策略是可行的。

如图7(b)所示,两种控制策略下,采用ECMS控制策略在运行350 s时消耗了氢气36 g,而采用经典PI控制策略消耗了氢气38 g。明显使用ECMS控制策略减少了氢气的消耗,提高了燃料经济性。

图7 两种控制策略下的燃料消耗、锂电池SOC对比

3.3 动力源运行压力分析

动力源运行压力是指各个动力源在混合动力系统中,当负载需求功率改变时,各个动力源为满足需求而更改输出电能的频率,频率越小,越有利于延长动力源的使用寿命[19]。

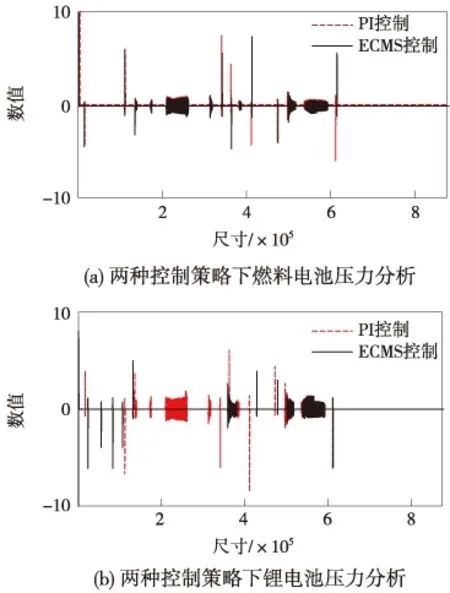
图8 两种控制策略下动力源压力分析

为了分析两种能量管理策略对动力源运行压力的影响,使用小波变换将各个电源的功率分解为高频部分和低频部分[20],两种控制策略下燃料电池和锂电池运行压力仿真结果如图8所示。可以看出,ECMS控制策略对动力源运行压力的分配更为合理,锂电池的运行压力明显减小,更有利于延长系统使用寿命。

3.4 直流侧电压

两种控制策略下,PI控制下的直流母线电压波动在±0.6%以内,ECMS控制下的直流母线电压波动更小一些,两种控制策略下的电压都满足供电要求(图9)。直流侧电压之所以变化是因为超级电容直接并联于直流侧,当高频率的负载需求由辅助储能单元提供时,超级电容提供的能量较多,导致电压变化。

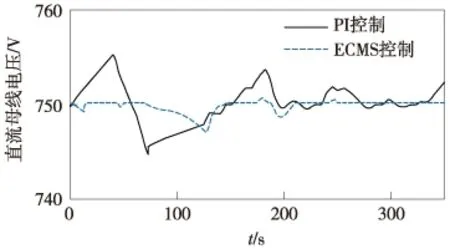
图9 直流侧电压

4 结论

(1)仿真结果表明,等效氢耗最小的控制策略比经典的PI控制策略节约系统燃料,有效改善了系统的燃料经济性。

(2)ECMS控制策略对各动力源间的功率输出和运行压力实现合理的分配,有效减轻锂电池的运行压力,起到延长锂电池使用寿命的作用。

(3)燃料经济性和日常运营成本在一定程度上受驾驶循环的影响。后续研究应重点关注驾驶循环对车辆性能的影响。