地铁列车作用下软黏土的动力响应试验研究

匡月青,陈页开,董浩喆

(华南理工大学土木与交通学院,广州 510640)

1 概述

在软黏土广泛分布的珠江三角洲地区,随着城市化进程的推进和公共交通规划需求量的日益提高,许多地铁工程不可避免地建设在软弱地基之上。在这样的地区修建地铁,若软基处理不当,在地铁运营期在列车荷载的作用下易出现路基变形的现象,严重时导致土体强度降低,甚至造成路基的失稳破坏,直接影响线路运行寿命并增加成本。为能有效控制或缓解该地区软黏土路基在地铁列车荷载作用下的变形,则需要对该地区土体的动力特性进行研究,比如动强度、动应力-动应变关系和动模量特性等。

目前,中外学者主要通过动三轴试验模拟地铁列车作用下动力特性。例如,Hyodo和Yasuhara[1]对日本Ariake 饱和软黏土进行低频循环荷载试验,引入相对循环应力比,提出了预测周期循环荷载作用下残余应变的计算模型。Chai和Miura[2]对日本Saga机场道路的软基进行动三轴试验,提出了交通荷载作用下软土的附加沉降计算公式。宫全美等[3]、 唐益群等[4]和骆俊晖[5]对南京地铁的软基进行动三轴试验,分别研究了土体的临界动应力比和临界动应力、动应力-动应变关系以及软土动力参数一振次关系变化规律，并建立动剪切模量随振次关系函数。唐益群等[6]、闫春岭等[7]、徐毅清等[8]、姜洲等[9]分别对上海地铁软基进行动三轴试验,分析了加载排水状态对土体变形特性的影响，对地铁隧道周边软土变形影响最大的是动 应力幅值，不同因素对动弹性模量的影响，建立了K0固结条件下软黏土累积塑性应变计算公式。刘添俊等[10-13]研究了珠海地区循环荷载作用下软黏土的应变速率特性、蠕变特性以及加载方式的影响。

以上研究存在以下不足：其一,由于不同地区的软黏土存在差异,对广州地铁列车荷载作用下软黏土动力特性研究甚少；其二,已有的关于珠三角地区软黏土动力特性的成果考虑的频率大多集中在0.5～1 Hz,未考虑高频荷载的影响。

针对以上不足,选取广州地铁某在建沿线路段的软黏土地基进行室内动三轴试验,模拟地铁列车荷载作用下软黏土动力特性,研究不同地铁动应力幅值和高频作用下饱和软黏土动强度、动应力-动应变关系和动模量特性,并通过Hardin-Drnevich模型验证本文通过实验数据得到的新的归一化的试验参数是合理可靠的,期望为该地区同类工程的建设治理提供合理的参考依据。

2 试验内容和方法

2.1 试验土样

试验土样取自广州某在建地铁工程沿线路段软土地基,为典型的珠江三角洲软黏土。取得土样后,按照TB10102—2010《铁路工程土工试验规程》中的规定制备重塑淤泥质软黏土,具体制备和加载过程是：风干、碾碎、过筛、烘干、加水、分层击实、饱和、固结、加载。饱和阶段先抽真空80 min,继续保持抽气状态缓慢进水20 min,经负压静置12 h后,使土样饱和度达到98%以上。试样直径为39.1 mm,高80 mm,其主要物理技术指标和静三轴强度指标见表1。试样制备过程中,固结完成的标志为1 h内的体积变形小于0.1 mL。

表1 重塑饱和软黏土物理技术指标

2.2 试验方案

室内试验使用的仪器为DDS-70动三轴仪,如图1所示。采用正弦波形对地铁列车荷载模拟,围压取100 kPa。

图1 DDS-70动三轴仪

文献[14]的研究成果表明,地铁列车对土体的振动作用主要取决于它所施加的动荷载和振动频率。考虑列车及轨道体系施加给路基的附加应力为30 kPa±10 kPa,本次试验的动应力幅值取10,20,30,45 kPa。

根据地铁现场实测数据[15],地铁列车经过时所引起的土体响应频率有高频和低频两种,即高频2.4～2.6 Hz,低频0.4～0.6 Hz,由于试验条件限制,本文重点研究高频,振动频率设为1,2.5,4 Hz。动三轴试验方案汇总见表2。

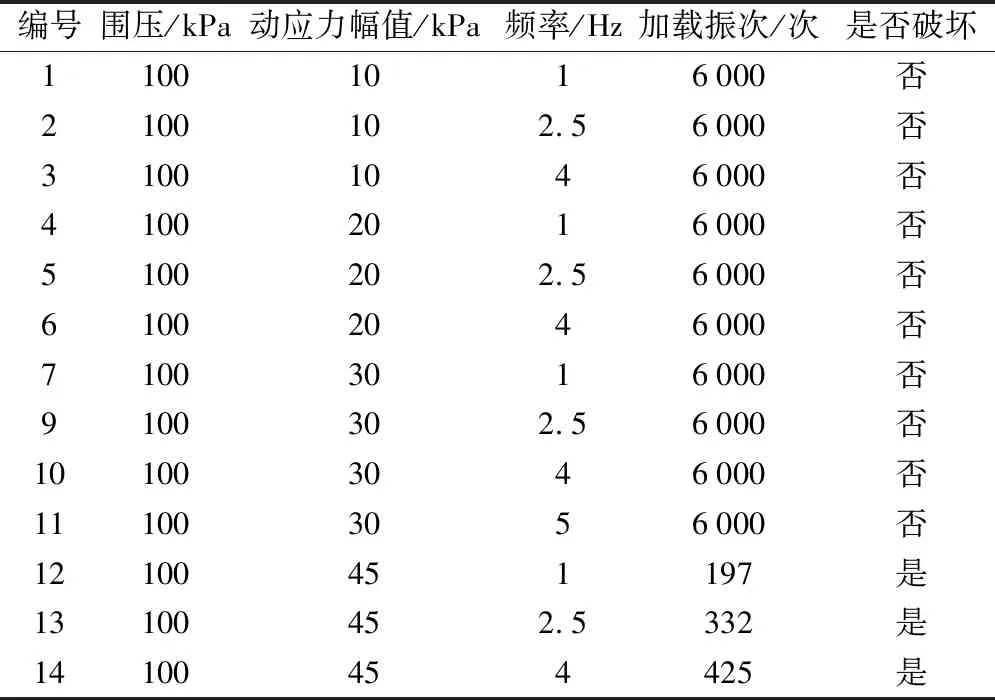
表2 饱和软黏土动三轴循环试验方案

为提高试验数据的可靠性,对每一编号所对应的方案都分别进行3组平行试验。试验结束的判断标准为当振次达到6 000次或轴向应变εd达到5%。

3 试验结果及分析

3.1 动强度及轴向应变分析

图2为轴向动应变幅值随振次变化的关系。从图2可以看出,该软黏土动强度<45 kPa,且稳定型和破坏型εd-N曲线的变化规律不一致。当动应力幅值σd<45 kPa 时,轴向动应变随振次的增加而先快速增长,之后其动应变增长速度随着的振次的增加逐渐减小,在振动结束即N=6 000次时,轴向应变εd远远小于5%,呈稳定趋势。而当动应力幅值σd达到45 kPa时,动应变随振次的增加不断增长,处于不断发展的状态,在振动初期便达到破坏应变即εd=5%,使土体产生破坏。动应力幅值相同时,轴向动应变随频率的增大而减小,主要归因于频率越大使列车作用于土体的时间越短,因此产生的变形减少。而频率相同时,轴向动应变随幅值的增大而增大,说明应该严格控制列车载重,以防超载对路基土体产生不利影响。而在地铁实际工程中,路基土体所承受的动荷载循环次数很大,动应力幅值应小于土体的破坏动应力[16],因此本文重点研究动应力幅值σd<45 kPa的试验结果。

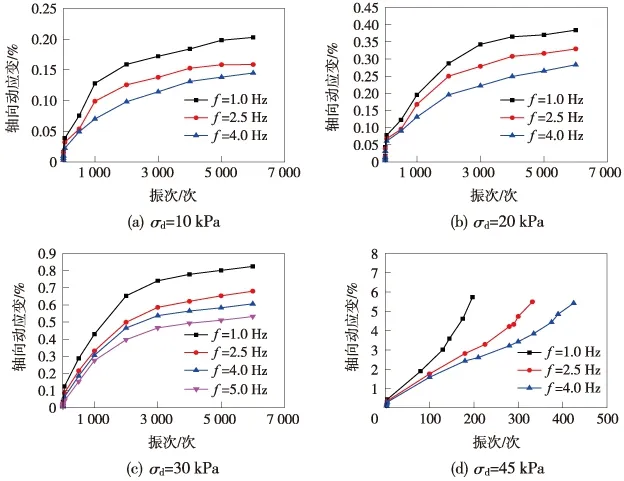
图2 不同条件下的轴向动应变-振次关系曲线

3.2 动骨干曲线分析

动骨干曲线是指不同振动周期作用下滞回圈顶点的连线,表示每个滞回圈动应力幅值-动应变幅值的关系,是研究土体动本构关系的重要依据[17]。

图3为不同动应力作用下不同频率的动骨干曲线。由图3可知,土体的动应力随动应变的增大呈非线性增大。当频率相同时,动应变增长速率随着动应力的增大而增大,但由于塑性变形的出现,所有动骨干曲线的应力增加速率越来越慢,并最终趋于稳定,说明在动应力幅值低于动偏破坏应力的情况下,土体呈现出应变硬化的性质。当动应力幅值相同时,存在一个极限动应变值,即作用的频率最大所对应的动应变εr,当εd<εr时,骨干曲线变化规律基本一致,说明此时频率对土样的动应力-动应变关系影响较小；当εd>εr时,骨干曲线往应变增大的方向延伸长度随频率的减小而增大,这归因于频率越低,加载速度越慢从而延长作用时间,则土体产生的轴向变形越大。

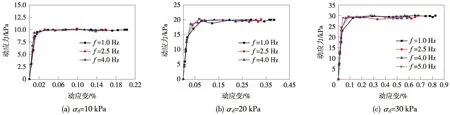
图3 不同动应力幅值下的动骨干曲线

3.3 动模量特性分析

在循环荷载作用下,土体的动骨干曲线可用Hardin-Drnevich[18]的双曲线模型表示

(1)

动模量是土体动力学的主要参数之一,是研究土体动力变形的重要依据。根据Hardin-Drnevich的双曲线模型,动弹性模量定义为

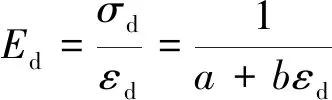
(2)

或

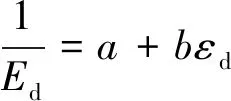
(3)

式中，Ed为动弹性模量；σd为动应力；εd为动应变；a、b为拟合参数。

图4和图5为不同试验条件下土体的Ed-εd关系曲线。可看出,动弹性模量随轴向的动应变的增大而减小,说明随着地铁运营时间的延长,在地铁列车荷载的循环作用下土体刚度不断减小,逐渐出现软化的现象。从图4可看出,当动应力幅值相同时,在振动初期,动弹性模量随频率的增大而增大；在振动中期,频率对动弹性模量的影响较小,曲线的规律出现较好的归一性；在振动后期,由于频率的不同而引起时间效应的影响,动弹性模量的衰减程度随频率的增大而增大。由图5可知,作用的频率相同时,土体动弹性模量随动应力幅值的增大而增大,说明当作用的地铁荷载不足以让土体产生破坏时,土体的压实度随列车荷载的增大而增大,更利于保护路基。

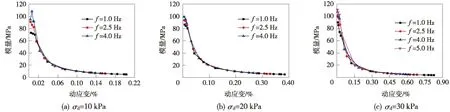
图4 不同动应力幅值作用下Ed-εd关系曲线

图6为不同条件下1/Ed-εd的关系,不同试验条件下的1/Ed随εd的增大线性增加,且在同一频率作用下的1/Ed增长速度随动应力的增大而减小。

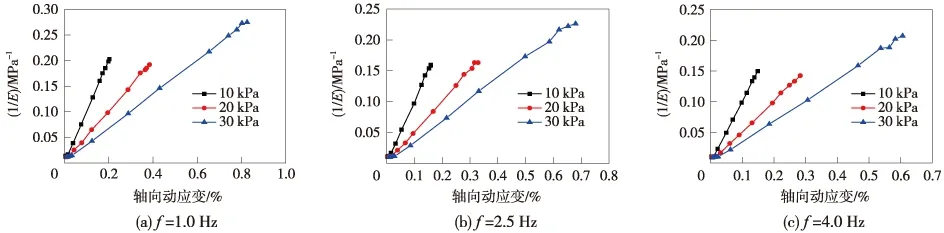
图6 不同频率作用下1/Ed-εd关系曲线

采用公式(3)对图6中的1/Ed-εd试验数据关系曲线进行回归分析,得到的拟合参数汇总于表3。结果显示,所有的曲线拟合度R2均大于0.996,说明采用Hardin-Drnevich的双曲线模型拟合广州地铁软黏土的动骨干曲线是合理的。

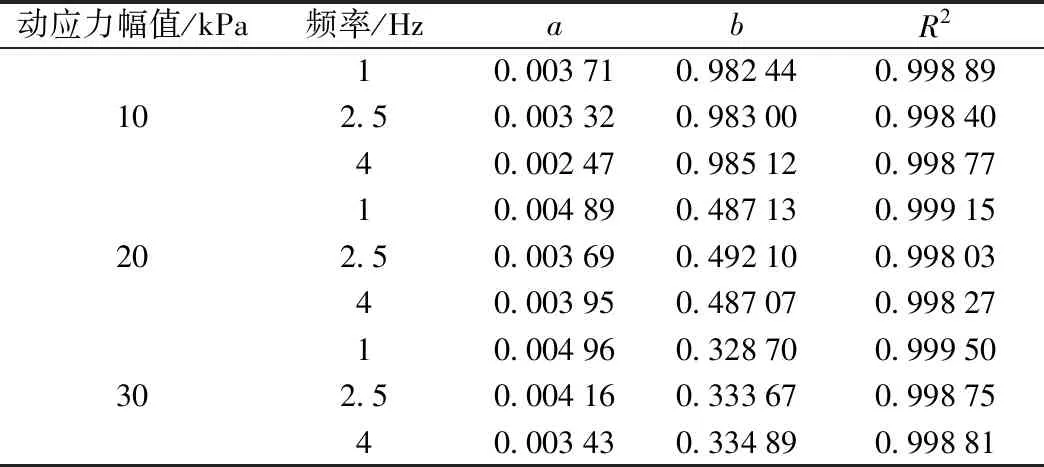
表3 不同条件下的模型参数拟合结果

从表3可知，当作用的动应力幅值相同时,不同频率下参数a、b受频率影响较小,大小基本相同,通过归一化处理,可取其平均值。不同试验条件下新的归一化拟合参数取值见表4。

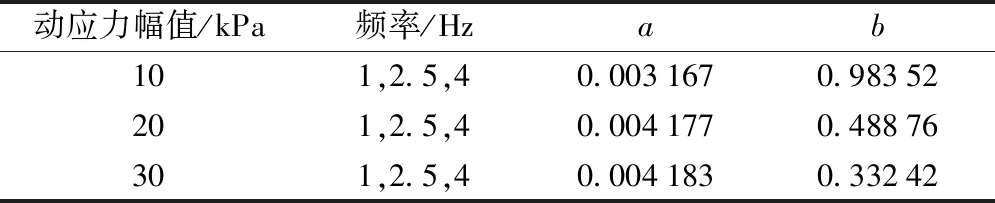
表4 新的归一化拟合参数值

3.4 模型拟合验证

结合公式(3)和表4对图6中不同试验条件下的试验数据1/Ed-εd曲线验证如图7所示。从图7可看出,不同试验条件下的试验数据与采用新的归一化拟合参数的Hardin-Drnevich 双曲线模型具有很好的一致性,而且各拟合相关系数R2均大于0.98。说明基于地铁列车荷载作用下饱和软黏土动模量特性的研究是合理可行的,研究结果可以为广州地区同类地铁工程软土的治理提供参考。

图7 1/Ed-εd试验数据曲线与H-D模型对比

4 结论

通过对广州地铁饱和软黏土进行室内动三轴试验,研究地铁列车荷载作用下土体的动力特性。基于试验结果,分析了动应力幅值和加载频率对土体动模量的影响,得到以下结论。

(1)在循环荷载作用下,该软黏土动强度低于45 kPa,稳定型和破坏型εd-N曲线的变化规律不一致。

(2)不同试验条件下的动骨干曲线规律较为一致,均呈明显的非线性应变硬化特征。当动应变低于动应变极限值,频率对动骨干曲线的影响较小。

(3)当其他条件相同时,在振动初期,动弹性模量随频率的增大而增大；在振动中期,频率对动弹性模量的影响较小,呈现较好的归一性；在振动后期,由于频率的不同而引起时间效应的影响,动弹性模量的衰减程度随频率的增大而增大。

(4)当其他条件相同时,土体动弹性模量随动应力幅值的增大而增大,说明当作用的地铁列车荷载不足以让土体产生破坏时,土体的压实度随列车荷载的增大而增大,更有利于保护路基。

(5)通过H-D模型验证本文通过实验数据得到的新的归一化的试验参数是合理可靠的,而且得到新的模型参数可为该地区同类地铁工程软黏土动力特性的研究提供参考。