非结构混合网格鲁棒自适应技术

唐静，崔鹏程，贾洪印,*，李彬，李欢

1. 中国空气动力研究与发展中心 计算空气动力研究所， 绵阳 621000

2. 西北工业大学 航空学院，西安 710072

近20年来，CFD已成为研究空气动力学的主要手段之一，并获得了工业部门的广泛认可。然而，CFD在飞行器跨声速气动特性计算、大迎角失速特性预测等方面仍面临着较大的挑战。CFD计算结果受数值格式、湍流模型和计算网格的影响很大。工程上常用的数值格式和湍流模型相对比较固定，且通过大量的研究和广泛的应用获得了较为详细的参数影响规律。然而，由于针对复杂外形的网格生成数学理论的欠缺，造成网格生成算法不完善，网格生成仍需要较多的人工干预。计算网格已成为影响CFD模拟精准度的关键因素[1]，显著影响着飞行器气动、控制和动力等性能的预测精度。

网格生成的单元疏密分布依赖于对流动特征的先验估计。工程问题中流动状态通常很多，针对每个流动状态生成对应网格的工作量太大。因此，与流场耦合、在计算过程中自动优化网格疏密分布的网格自适应技术得到了国内外研究人员的广泛研究。美国NASA的报告《2030年CFD展望研究》明确将网格自适应技术列为亟待发展的一项关键技术[2]。

网格自适应技术的研究大约起步于20世纪80年代[3]，经过近40年的发展，在网格单元误差估计[4-5]、网格分布优化[6]、物面网格几何投影等方面都取得了较大的进展[7]。然而，由于鲁棒性不足(尤其是附面层内半结构化网格)和几何保形实现难度大等问题，网格自适应技术还未能广泛应用于工程问题中[7-8]。

网格分布优化通常包括r型自适应和h型自适应两种类型。r型自适应仅移动网格点，网格的拓扑结构和单元连接关系在自适应过程中保持不变。由于不增加网格单元的总量，r型自适应改变网格分布的能力有限。h型自适应则是通过局部区域网格单元的剖分加密或合并稀疏的方式优化网格分布，以提高关键区域流动模拟的精度。

四面体网格生成算法相对成熟[9-10]，因而四面体网格h自适应方法的成熟度较高[11]，还可以给定网格尺寸场开展各向异性的自适应[12]。四面体网格主要应用于无黏流动，当扩展到黏性流动时，物面附近需要采用层结构的各向异性四面体网格单元[13]。黏性流动的模拟更多地采用非结构混合网格，其h型自适应技术的难点集中在附面层内层结构网格的处理。

Alrutz[14]采用固定层结构网格的策略，只针对四面体网格开展自适应，不能改变附面层网格的分辨率。Joubarne[15]和Lepage[16]等对四面体采用h自适应，对附面层网格则采用y+自适应，只能在法向高度方向改变网格的分辨率。Park[17]将棱柱和金字塔单元都转化成四面体进行处理，李立等[18]在纯四面体网格上开展h自适应后再重新生成层结构网格，这两种方法可改变层结构网格的流向尺寸分布，但前者失去了六面体或三棱柱网格模拟黏性流动的精度优势，后者层结构网格的生成原本就是网格生成的难点。

为了同时改变层结构网格物面法向和切向的尺寸分布，更有效的方法是采用网格剖分方法。按自适应后网格单元类型，自适应可以分为标准单元类型、悬空节点类型和多面体单元类型。标准单元类型方法需要剖分临近单元以消除悬空节点，层结构内的网格通常只能沿着物面法向方向剖分并“贯穿”整个层结构以改变物面切向方向的网格尺寸[19-20]，改变法向尺寸多采用y+方法[21]。该类方法自适应后网格保持了完整的层结构，但要求初始网格的层结构清晰，且在处理金字塔单元时可能出现剖分方式不能自洽的问题。

悬空节点类方法对网格单元剖分方向不作任何限制，但要求流场解算器能处理悬空节点。该类方法可分为基于网格面和基于网格单元两类。基于网格面的方法[22-23]可在一定程度上实现网格各向异性分布，但通常网格单元的几何质量随着自适应迭代下降很快。基于网格单元的方法既可用于各向异性的网格自适应[24]，也可用于各向同性的网格自适应[25]，后者网格单元剖分类型很少，对数据结构的依赖较轻，软件实现更容易。

多面体单元类型的自适应[26-27]将带有悬空节点的标准单元转换成多面体单元，不需要对相邻单元进行额外的处理，消除了网格单元之间的相互影响，鲁棒性更高。多面体类型也可类似地分成基于网格面[26]和基于网格单元两种子类型[28]。

表面网格加密后，新增网格点通常不在几何曲面上，需要将其投影到物面上。物面几何信息可通过几何系统(CAD)直接获得[28]，也可通过初始表面网格拟合成的近似曲面得到[29-30]。前者能将新增网格点精确投影到真实几何上，但对于复杂外形容易出现投影多解或网格交叉等问题。拟合曲面与真实几何有一定的偏差，但消除了自适应方法对CAD系统的依赖。依据采用网格单元的模板大小，拟合方法可分为局部曲面拟合[29]和非局部曲面拟合[30]两种类型。非局部曲面拟合需要使用较大区域内的表面网格信息和采用分片高次拟合。局部曲面拟合只使用当前表面网格单元的顶点信息，如局部Coons曲面[29]。

一般情况下，物面附近的层结构网格单元法向尺寸远小于切向尺寸，表面网格点发生微小的法向移动都可能造成物面附近的网格单元出现重叠交错等严重问题。因此，表面网格投影后需要对体网格单元进行重构或移动变形，确保计算网格有效。复杂外形的棱柱网格重构难度很大，且鲁棒性通常不高。通过移动体网格顶点的网格变形技术更加高效，但要求采用的网格变形技术能有效处理棱柱层网格[31]。

本文以工程实用为目标，发展了网格自适应系统涉及的网格分布优化、网格几何投影和空间网格匹配3项关键技术，建立了鲁棒的非结构混合网格自适应方法。首先，在多面体网格自适应方法的基础上，发展了标准网格面的网格分布优化方法，提高了方法的通用性，解决了物面网格投影造成的“缝隙”问题。其次，通过Hermite插值方法构造了局部Coons曲面，采用参数化投影方法实现了表面网格的快速投影。最后，采用改进的距离函数动网格方法实现了空间网格与投影后表面网格的协调匹配。

1 网格单元加密或稀疏的自适应判据

流场是构造网格单元自适应判据的基础，本文流场求解采用自主研发的MFlow软件[32]。该软件采用二阶格式的有限体积方法求解积分型的雷诺平均Navier-Stokes方程。文中对流通量采用Roe格式[33]，黏性项离散采用中心差分，时间项离散采用LU-SGS方法[34]，湍流模拟采用一方程SA模型[35]或RC修正形式的SA模型[36]。

1.1 拟梯度自适应判据

拟梯度自适应判据的理论依据假定流场梯度大的区域计算误差更大。本文采用密度ρ、压力p、速率|v|和温度T4个流场变量加权的形式。为了避免流场变量数值量级差别大造成权值取值困难的问题，本文采用远场流场值(下标∞表示)进行无量纲化，则加权流动变量可表示为

(1)

式中：|v|为流动速度矢量；w1～w4分别为4个变量的权值。进一步考虑网格尺寸因素，本文拟梯度计算采用的形式为

(2)

式中:下标1、2分别指网格面两侧的单元;d12为体心间的距离; 上标s为距离的影响因子，s值越大距离影响越大，一般取值范围为-1.0～1.3。特别地，当s取-1时，类似于采用近似一阶数值方法计算梯度。则相邻网格单元中最大梯度值gm为

(3)

式中:NF为面相邻网格单元的总数。

遍历所有网格单元得到gm的最大值gmax，给定自适应加密和粗化的阈值参数tr和tc，则加密和粗化的临界梯度值为

gr=gmaxtr,gc=gmaxtc

(4)

当某网格单元的gm大于gr时标记为加密，当网格单元的gm小于gc时,标记为粗化，其他的网格单元保持不变。

1.2 剪切应变率自适应判据

剪切应变率自适应判据[37]主要用来识别流场中的分离旋涡，由Q判据进行无量纲化得到,即

(5)

式中：ω和S分别为速度梯度的旋转分量和剪切分量，定义为

(6)

由于自由来流的S值相对很小，剪切应变率 计算可能会产生数值噪声，造成旋涡区域的误判。本文采用应变过滤方法消除数值噪声，则判定网格单元处于旋涡区域还需要满足如下条件：

(7)

式中：ε为过滤阈值；N为网格单元总数；h取值0.1～0.5。

2 网格单元分布优化方法

本文采用剖分或合并网格单元的方法实现网格分布的优化。为提高网格加密或粗化操作的运行效率，应建立合适的数据结构。

2.1 网格细化方法

本文综合考虑加密方法的鲁棒性和效率，选择各向同性加密网格单元，则每类单元对应着唯一的加密模式。并且，除金字塔单元外，其他类型网格单元加密后的子网格单元具有自相似性，即子单元类型与父级单元相同。各类型的网格单元加密方法如下：

1) 三角形剖分为4个三角形，见图1(a)。

2) 四边形剖分为4个四边形，见图1(b)。

3) 四面体剖分为8个四面体，见图1(c)。

4) 三棱柱剖分为8个三棱柱，见图1(d)。

5) 六面体剖分为8个六面体，见图1(e)。

6) 金字塔剖分为6个金字塔和4个四面体，见图1(f)。

图1 非结构混合网格单元加密模式

定义1自适应层级某网格单元的自适应层级是指由初始网格单元得到该网格单元需要加密的次数。

相邻两个单元层级不同时，在两个单元的交界面或交界线上将出现图2所示的悬空节点。由于常规流场模拟软件不支持悬空节点，为了提高网格自适应方法对流场模拟软件的通用性，采用多面体转换方法间接消除悬空节点。以图2左侧单元为例，转化为多面体后共包括9个面：F1:{1,2,6,5},F2:{4,a,c,b},F3:{a,3,d,c},F4:{b,c,e,8},F5:{c,d,7,e},F6:{1,2,3,a,4},F7:{2,3,d,7,6},F8:{6,7,e,8,5},F9:{1,4,b,8,5}。其中，前5个面为标准的四边形，后4个面为包含5个顶点的多边形。一般情况下，基于非结构网格的流场模拟软件只支持三角形和四边形两种标准网格面单元。因此，为了进一步提高自适应系统的通用性，本文将多边形面转换成多个三角形和四边形。对于三角形面，标准化转换共有3种拓扑类型，如图3所示；对于四边形面，共有5种拓扑类型，如图4所示。

图2中定义多面体的后4个多边形网格面都包括5个网格顶点，每个多边形标准化后剖分成3个三角形单元，因此该多面体单元标准化后最终包括17个面，如图5所示。

图2 悬空节点示意图

图3 非标准三角形网格面拓扑类型

图4 非标准四边形网格面拓扑类型

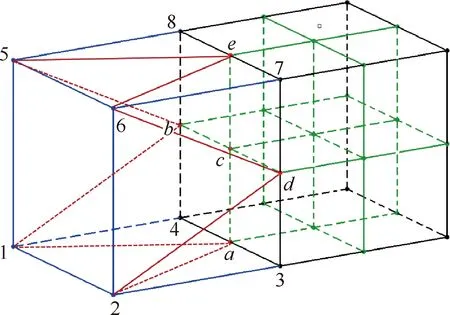
图5 多面体单元多边形网格面标准化示意图

2.2 网格粗化方法

本文网格粗化方法采用“回退”方法，即网格粗化是网格加密的逆向过程。因而只有当某网格单元经过加密后生成的所有子网格单元都被探测器标记为粗化时，该网格才回退到加密前状态。

由于相邻网格单元体积的比值过大会降低CFD求解的收敛速度和稳定性，因此通常需要对相邻单元的层级差进行限制。另外，同时具备网格细化和粗化功能时，自适应属性的标记可能出现矛盾情况，即同一网格单元被探测器标记为粗化，却由于层级差限制需要加密。因此，本文自适应方法增加了自适应加密/粗化准则。

准则1自适应加密/粗化准则某网格单元自适应加密或粗化属性的标记满足如下3条规则：

1) 层级差限制规则。共面相邻的网格单元层级差不超过1，否则，加密相邻层级较低的网格单元。

2) 网格光滑性规则。当与某个单元共面的所有单元都标记为加密属性时，该单元也标记为加密属性。

3) 加密优先规则。当某个网格单元标记为粗化却因规则1)或规则2)需要标记为加密时，加密标记优先于粗化。

2.3 网格自适应的数据结构

由于本文网格粗化方法采用网格加密的逆向操作，因此从初始网格到最细网格，包括中间过程的网格，都需要记录和存储。各层级的网格还需要建立父级-子级的对应关系，以便实现粗化操作。多级的粗、细网格形成自然的树形数据关系，并且由各类单元加密模式可知父-子级网格单元是一对多的关系，因此可以采用多级多路的树形数据结构处理由最粗网格单元到最细网格单元之间的层级关系。

3 表面网格几何投影方法

实际应用中物面通常为曲面，因此表面网格加密后新增加的网格点通常不在物面上，需要将其投影到物面或重构的近似物面上。

3.1 物面几何重构

本文物面几何重构方法采用局部Coons曲面拟合，该方法只依赖于表面网格点坐标和相应的法向矢量。法向单位矢量通常不是标准的网格数据，本文通过与网格点直接相连的面网格的法向加权得到，即网格点i的法向向量ni为

(8)

式中：nk和Sk分别为网格面k的单位法向量和面积；Nk为与网格点i相连的网格面总数。

局部Coons曲面拟合的基本思想是先通过表面网格点和法向信息重构网格边对应的三维边界曲线，然后通过边界曲线的融合构造三维曲面。

本文采用三次Hermit插值直接构造三维边界曲线。如图6所示，表面网格边两个顶点的坐标为x1和x2，相应法向为n1和n2，参数化的边界曲线c(t)为

c(t)=f1x1+f2x2+g1τ1+g2τ2

(9)

式中：f和g为权值；τ为相应切向修正量，即

d1=x2-x1,d2=x1-x2

(10)

针对三角形和四边形两种表面网格单元，边界曲线构造方法相同，但曲线融合成曲面的方法有较大差别，本文基于文献[29]中的方法，针对三角形和四边形分别采用如下的融合方法。

对于三角形网格面，如图7所示，3个网格点为x1～x3，相应法向为n1～n3。首先将三角形x1x2x3转化到标准三角形参数平面V1V2V3，V1V2方向参数为S′，V1V3方向参数为S″。网格边x1x2构成边界曲线c1，网格边x2x3构成边界曲线c2，网格边x1x3构成边界曲线c3，则三维拟合曲面S(S′,S″)表示为

S(S′,S″)=0.5(Xa+Xb+Xc-Xt)

(11)

图6 三维边界曲线重构示意图(虚线：网格边，实线：重构的边界曲线)

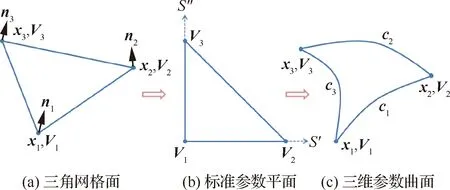
图7 三角形网格曲面重构示意图

图8 四边形网格曲面重构示意图

对于四边形网格面，如图8所示，4个网格点为x1～x4，相应法向为n1～n4。类似地，首先将四边形x1x2x3x4转化到标准四边形参数平面V1V2V3V4，V1V2方向参数为S′，V1V4方向参数为S″。网格边x1x2构成边界曲线c1，网格边x2x3构成边界曲线c2，网格边x4x3构成边界曲线c3，网格边x1x4构成边界曲线c4，则三维的拟合曲面S(S′,S″)表示为

S(S′,S″)=Xa+Xb-Xt

(12)

3.2 新增网格点投影

本文拟合曲面为参数曲面，可以采用参数点映射方法实现新增表面网格点的几何投影，即先在标准参数面上取投影点的参数坐标，然后代入参数曲面方程求得投影点在曲面上的坐标点，最后将新增网格点移动到目标点位置。

如图9所示，对于三角形网格面，常用的新增表面网格点的位置为N1、N2和N3，对应参数坐标为

图9 网格参数曲面和新增点参数

(13)

对于四边形网格面，常用的新增点位置为N1、N2、N3、N4和N5，对应参数坐标为

(14)

4 空间网格匹配方法

因模拟黏性流动的需要，附面层内紧邻物面网格的法向尺寸远小于其他两个方向的尺寸，新增表面网格点投影后，极有可能造成物面附近棱柱网格单元出现重叠交错的问题，如图10所示，因此必须对空间网格点进行处理。网格变形技术不改变网格拓扑和不增减网格点数，通用性好，其中计算速度最快的一类方法是基于距离函数的动网格方法。

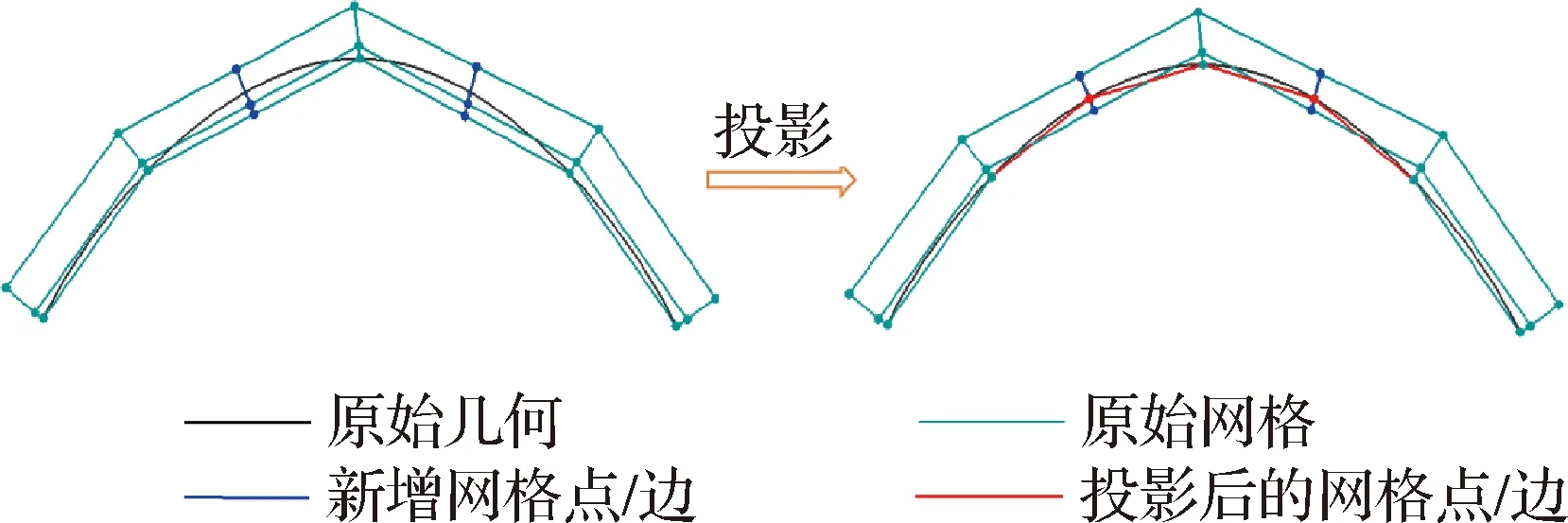
图10 表面网格投影造成网格单元重叠交错示意图

本文采用改进型的基于距离函数的动网格技术实现表面网格投影后体网格单元的快速匹配。该方法通过引入自调节的影响半径大大提高了附面层内半结构化网格的变形能力，同时通过包围盒加速技术提高了变形方法的计算效率。

给定表面网格点变形量Δxi,S，体网格点坐标变化量Δxj,V表示为

(15)

式中：NS为表面网格点总数；N为体网格点总数；η为衰减函数；ωi为表面网格点i的权值。衰减函数和权值的取值方法以及更多细节信息可参考文献[31]。

5 网格自适应方法数值验证

5.1 30P30N三段翼构型绕流自适应模拟

30P30N三段翼构型广泛应用于CFD数值方法的验证，主要考察数值方法对尾迹剪切层的模拟能力。图11给出了其几何构型[38]和风洞试验选择的6个速度型测量位置。计算来流状态为：单位雷诺数Re=1.61×107，马赫数Ma∞=0.2，静温T∞=288.15 K，迎角α=19°，采用的湍流模型为标准一方程SA模型。计算采用六面体为主的非结构混合网格，如图12所示，其翼型主翼周向共251个网格点，前缘缝翼和后缘襟翼分别有131和151个网格点。法向第1层网格高度为2×10-5m，网格增长比为1.12，展向共2个网格点。

自适应计算共迭代3次，自适应判据采用基于速率的拟梯度方法，对应的参数tr=7×10-5，tc=0，s=-1.0，加权流场变量速率项权值为1，其他项为0。图13给出了自适应后的网格，由于流动速度在翼型附近和尾迹剪切层变化剧烈，因此网格在翼型附近和尾迹区都进行了加密。初始网格单元总数约为4万，由于流场模拟采用了三维网格，本文自适应直接采用三维网格加密方法，因而自适应后网格增量很大，约为970万。

图11 30P30N三段翼几何构型和6个速度型站位

图12 30P30N三段翼原始基准网格

图14给出了自适应模拟过程中密度残差收敛曲线，可以看出，自适应后残差收敛性更好。图15给出了翼型压力分布与试验值[38]及参考值[39]的比较，初始网格和自适应后计算的压力系数Cp分布与试验值吻合得都很好，且自适应后主翼和襟翼上表面的压力略低。

图13 30P30N三段翼自适应后的网格

图14 网格自适应迭代过程密度残差收敛曲线

图15 网格自适应前后翼型压力分布比较

图16～图18给出了图11所示第1、第3和第5这3个站位的速率分布，其横轴为采用自由来流值进行无量纲化的当地速率u/ainf，纵轴为点到翼型表面的无量纲法向距离(参考值为平均气动弦长)。综合来看，随着自适应迭代和网格在翼型附近加密，网格对流场的分辨率提高。与初始网格相比，自适应后速度分布与试验值吻合度明显提高，且本文计算结果比文献[39]中采用高阶格式计算的结果略好。

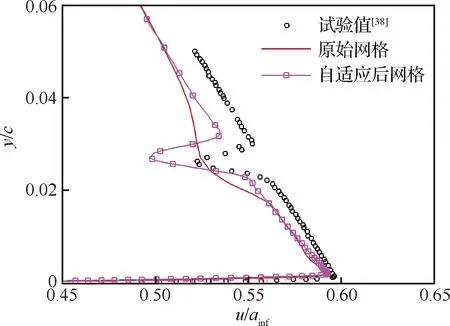
图16 网格自适应前后第1个站位处速度型分布比较

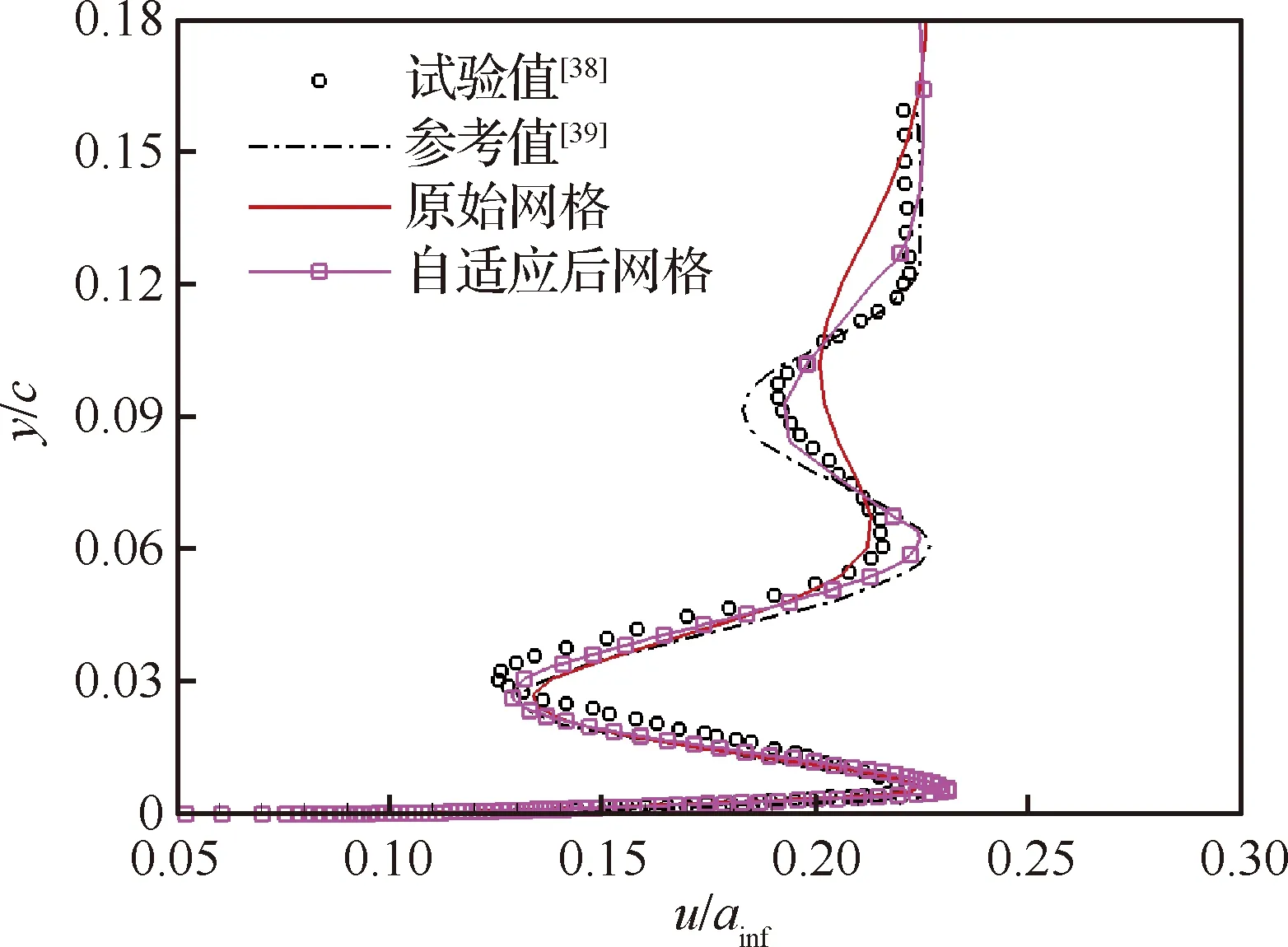
图18 网格自适应前后第5个站位处速度型分布比较

图19给出了自适应前后主翼前段区域的速率流场分布，前缘缝翼上表面产生的附面层低速气流和流过缝隙的高速气流在主翼前缘区域发生掺混。相比初始网格，自适应后网格尺寸减小，分辨率增加，因此网格的数值耗散小，前缘缝翼上表面附面层发展更充分，附面层更厚，掺混的两股气流剪切作用更强，因此能够更好地模拟出图16所示的速度型中向左的“凹坑”。由于第1个站位离主翼前缘不远，因此主翼的附面层相对很薄，流动速度在法向很小的距离内迅速增加，对应于图16中第1个峰值。

对于襟翼上表面区域，由主翼产生的附面层气流与流经襟翼前部缝隙的高速气流发生掺混，同时主翼上部的掺混区继续向后发展，因此襟翼上表面的速度型出现了两处向左的“凹坑”，如图18所示。类似地，通过网格自适应对网格进行加密后，速度型的模拟与试验吻合得更好。

图19 网格自适应前后主翼前段区域速度分布

5.2 三角翼大迎角绕流自适应模拟

后掠角65°尖前缘三角翼(VFE-2)常用于验证和评估CFD方法预测复杂分离涡的能力，其几何模型和试验测压站位[40]如图20所示。计算来流条件为：单位雷诺数Re=1.377×107，静温T∞=322.04 K，马赫数Ma∞=0.4，侧滑角β=0°，迎角α=20.17°，湍流模型为采用RC修正的一方程SA模型。

图20 三角翼几何构型和试验测压站位

图21 三角翼流场模拟的原始基准网格

图22给出了自适应迭代过程中密度残差收敛曲线，由于初始网格不能有效捕捉空间分离流动，密度残差收敛较慢且共降低约2个量级。自适应后密度残差收敛性明显改善，其收敛速度更快且下降更多。

图23和图24分别给出了x/c=0.6，0.95这2个站位等x截面上自适应前后网格对比，自适应后网格加密主要集中在主涡的涡核区域和旋涡脱离三角翼前缘后的强剪切区域。

图22 三角翼网格自适应过程密度残差收敛曲线

图23 自适应前后x/c=0.6截面处网格对比

图24 自适应前后x/c=0.95截面处网格对比

图25给出了三角翼x/c=0.6站位处上表面前缘附近自适应前后由网格代表的几何形状对比，整体来看，自适应加密并投影到拟合曲面后，前缘处的几何形状光顺且连续性好。从局部放大图可以看出，自适应后新增网格点投影后的位置几乎位于真实的几何曲线上。由此表明，基于一定的网格密度，本文曲面拟合技术能高精度地重构真实的几何曲面。

自适应前后分离涡附近的空间流线比较见图26，初始网格计算的分离涡在接近三角翼后缘附近发生了破裂，二次涡在后缘附近与主涡相互混合；自适应后主分离涡未发生破裂，主涡和二次涡向后运动的旋转流态都保持得很好，且彼此独立向后发展。

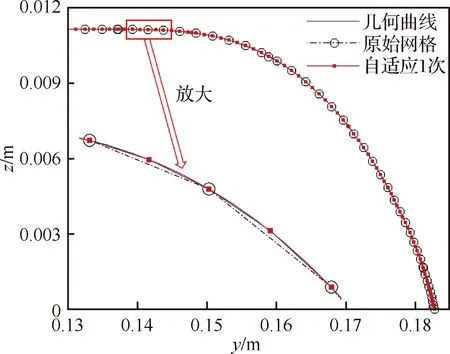
图25 三角翼x/c=0.6截面上表面前缘处网格自适应前后对比

图26 三角翼网格自适应前后空间流线对比

图27给出了x/c=0.6站位处自适应前后计算的压力分布与试验值[40]的比较，自适应后压力分布与试验吻合更好。图28给出了x/c=0.95站位处自适应前后计算的压力分布，由于自适应后主涡未发生破裂，计算的压力分布精度得到显著提升。

图27 自适应前后x/c=0.6截面处压力分布对比

图28 自适应前后x/c=0.95截面处压力分布对比

6 结 论

本文针对非结构混合网格，发展了网格单元分布优化、网格几何投影和空间网格匹配3项关键技术，建立了高鲁棒性、几何保真的网格自适应系统，并采用30P30N三段翼型和三角翼两个标准算例对自适应技术进行了验证。

1) 结合基于流场特征的自适应探测器，基于网格加密和粗化方法建立的网格单元分布优化技术能有效地实现计算网格的动态优化。

2) 基于仅依赖表面网格点信息的局部曲面拟合技术能高精度地重构物面几何信息，通过参数化目标点可实现新增网格点的快速投影。

3) 基于改进型的距离函数方法能有效解决因表面网格点投影造成的空间网格单元重叠交错的问题，实现空间网格单元与投影后的表面网格协调匹配。

4) 本文建立的网格自适应技术可以明显改善流场求解的收敛性和提高流场细节的分辨能力，如压力分布和速度分布等，从而提高飞行器气动特性的预测精度。

对于真实战斗机或运输机等更复杂的几何构型，网格单元总量可达到千万量级。并行计算是减少自适应系统运行时间的有效方法，因而下一步将针对网格自适应系统的并行化开展研究。