基于动力定位应用的直翼推进器水动力特性分析

（中国船舶及海洋工程设计研究院 上海200011）

引 言

直翼推进是船舶推进方式之一，直翼推进器在不改变整体转速的情况下推力大小和方向无级可调，正车倒车反应时间短，工作转速低故而拥有低噪声性能，锻造不锈合金钢材质耐腐蚀且强度高，能承受更高的冲击，同时具有良好的操纵性及机动性［1］，被广泛应用于拖船、扫雷舰艇等高动力定位控制要求的场合［2］。

福伊特公司是目前全球主要的直翼推进器生产厂商，我国尚未实现对直翼推进器的自主研发与生产。国产动力定位控制装备虽然从算法原理上与推进器的选择关系不大，但是其接口关系以及在船体上产生的定位效果均还没有得到实际验证，而国际上舰船专业控制厂商（如Congsberg公司等）在驱动直翼推进器的动力定位控制领域积累了大量的工程经验。

为打破国外在本领域核心技术的垄断局面，需要对直翼推进器的工作原理及实际应用开展研究。本文结合实船选用的直翼推进器型号、安装位置和倾斜角度等多方面因素，通过流场的CFD建模，对推进器的水动力特性进行了初步分析。该结果可为后续动力定位控制策略和算法研究以实现推力最大化或效率最大化提供参考。

1 直翼推进器工作原理

直翼推进器垂直安装于船舶脊线，叶片均匀分布于回转箱，叶片跟随回转箱绕推进器转轴O公转，同时绕自身轴线摆动。推进器通过内部机构控制使其所有叶片弦线的垂直线相交于某一定点，该点称为直翼推进器的控制点N，如图1所示。

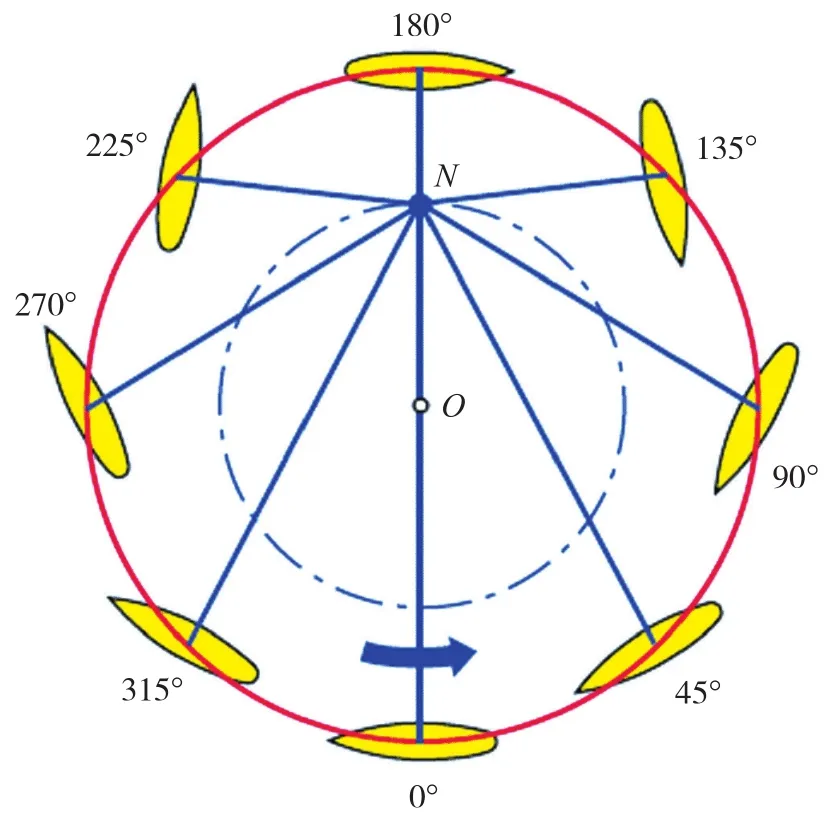
图1 直翼推进器控制点与叶片角度关系示意图

控制点N到推进器转轴中心O的距离称为偏心距偏心距与叶片公转半径R的比值称为直翼推进器的偏心率e［3］，如式（1）所示。

当N点与O点重合时，叶片弦线与切线速度重合，故而叶片与水流间的攻角为零，作用在叶片上的水流不产生作用力，船速为零；当N点与O点不重合并保持恒定时，推进器旋转一周，转轴中心点O前进距离即为螺距H=2πeR，此时保持船速V前进，控制点N所在的圆即摆线基圆。

当控制点从N调节到N′时，叶片弦线不再与轨迹相切，攻角不为零，叶片与水流间相互作用产生叶片升力，其在船体前进方向上的投影即为对于船体的推力，如图2所示。故而，通过改变控制点N的位置，即可改变叶片的运动规律，最终实现推力方向和大小的变化及控制。

图2 叶片与水流作用的作用力

直翼推进器叶片上叶片升力的形成原理与机翼理论相同。由于叶片上下表面与水流间形成压力差，故产生了相应的升力与阻力。根据相关理论推导得出升力公式（2）和阻力公式（3）［4］：

式中：CL为叶剖面升力系数；CD为叶剖面阻力系数；Ai为第i个叶片剖面面积，m2；ρ为水密度，kg/m3；V为叶片相对水流速度， m/s。

升力系数CL和阻力系数CD的大小与攻角α有关，在一定条件下，随着攻角α的增大而增大。

定义直翼推进器的进速系数J为式（4）：

式中：n为直翼推进器转速，r/s；D为推进器回转直径，m。

将各叶片的受力分解，推进器前进方向的分力（主推力T）相互叠加，垂直于前进方向的分力（侧推力S）相互抵消，最终其推力方向垂直于ON，且其推力大小与ON和NN′的大小有关。根据相关理论推导，主推力系数KT、侧推力系数KS、转矩系数KQ和效率η如式（5）～式（8）：

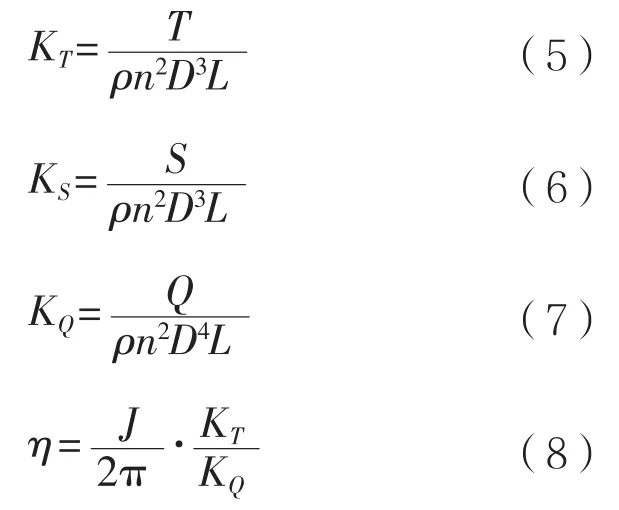
式中：T为主推力，N；S为侧推力，N；Q为转矩，N·m。

2 流场CFD建模及网格划分

2.1 几何模型参数

根据实船直翼推进器的参数，建立双推进器流场CFD模型。数值仿真参数如表1所示。

2.2 推进器几何模型网格划分

流场的计算域设定为：在各叶片附近以叶片转轴为圆心设置小圆，直径为800 mm；在推进器区域，以推进器中心为圆心设置大圆，直径为3600 mm；在直翼推进器外围设置矩形整体流域，宽为40000 mm，长为60000 mm，如图3所示。

采用非结构化网格对流场进行划分，并对叶片及推进器附近网格进行局部加密，在推进器外的整体流场采用较疏的网格，既保证计算结果的精确性又减少了计算时间，网格划分情况如图4所示。

表1 仿真模型参数

图3 简化的流场计算域

2.3 推进器仿真理论基础

由水的密度ρ（kg/m3）、Fluent初始设置参数V（m/s）、单个叶片面积A（m2）、推进器转速n（r/s）、回转直径D（m）、公称长度L（m）、进速系数J，以及经由Fluent仿真得到的初始主推力系数KT、侧推力系数KS、转矩系数KQ，可得到式（9）-式（18）的计算公式。

2.4 CFD模型的边界条件及计算参数设置

采用嵌入式滑移网格方法建立直翼推进器流场数值模型，同时通过UDF控制推进器和叶片按相应规律运动［5］。

结合直翼推进器的流场情况和嵌入式滑移网格方法，设置相应的出入口速度、壁面等边界条件，并在推进器的大圆线上和叶片附近的小圆线上设置滑移网格边界，具体边界条件设置情况如图5所示。

根据直翼推进器流场情况，设置求解模型、求解方法和相应参数，具体设置情况如表2所示。

3 水动力性能计算分析

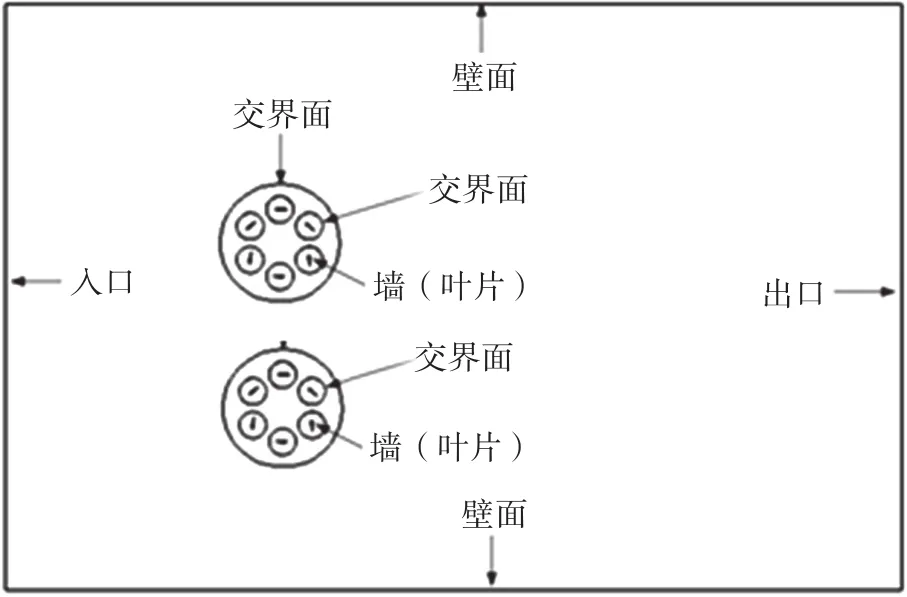
图5 流场边界条件设置情况图

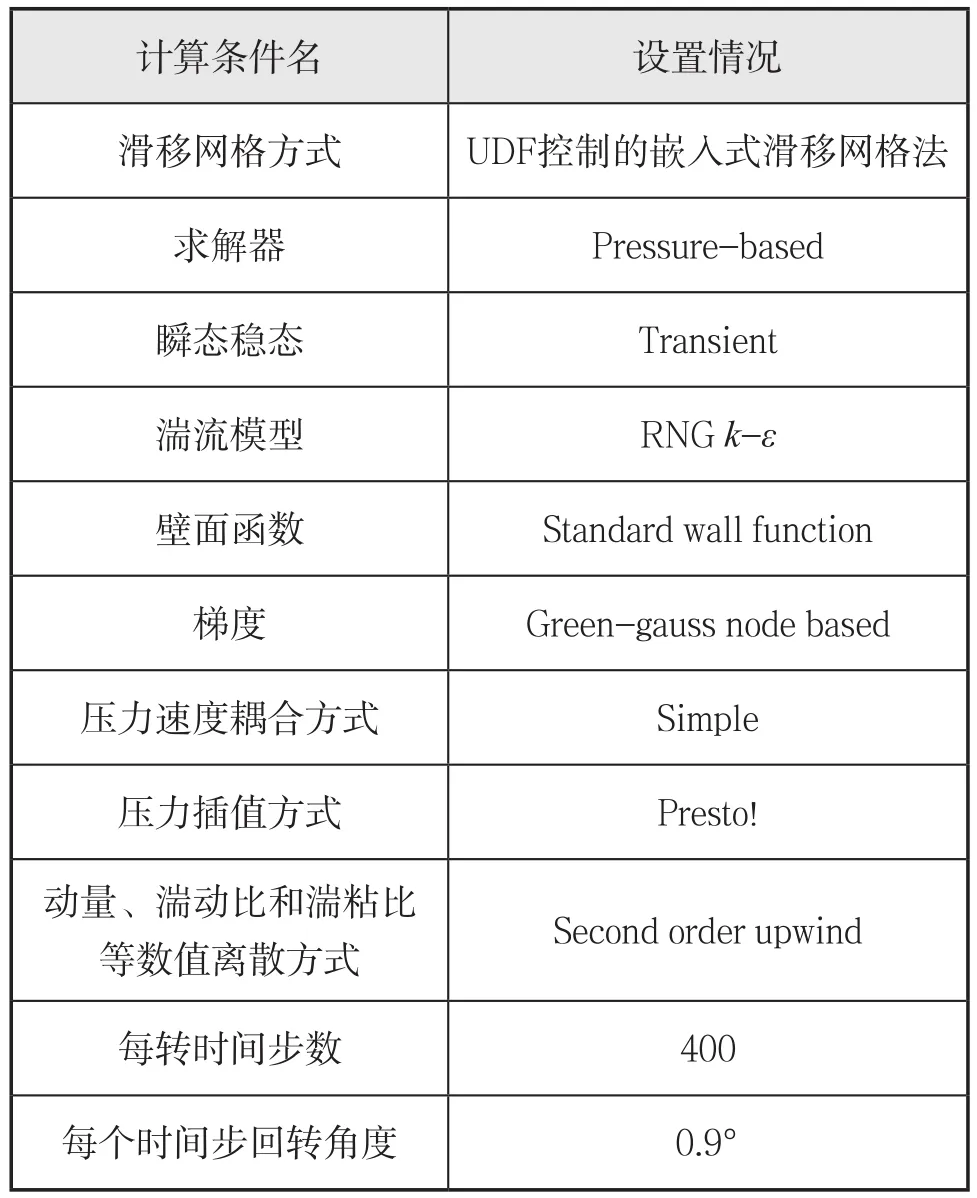
表2 计算条件设置情况

利用FLUENT进行推进器CFD仿真，采用嵌入式滑移网格方法，对推进器在不同进口速度和偏心率（e= 0.4，0.5，0.6，0.7，0.8）下的水动力性能进行求解和分析。鉴于文章篇幅，仅展示偏心率e = 0.6时不同进口速度时推进器的速度云图，如下页图6所示。图中下部推进器以50 r/min顺时针旋转，上部推进器以50 r/min逆时针旋转。

由图6可知，主推力随着入口速度v的增大而减小，当入口速度趋向于v=eωD/2时，推进器对水流作用最小，此时接近零滑脱状态。此外，由于流场区域内的速度云图成对称分布，故可认为直翼推进器顺时针旋转和逆时针旋转的水动力性能相同。

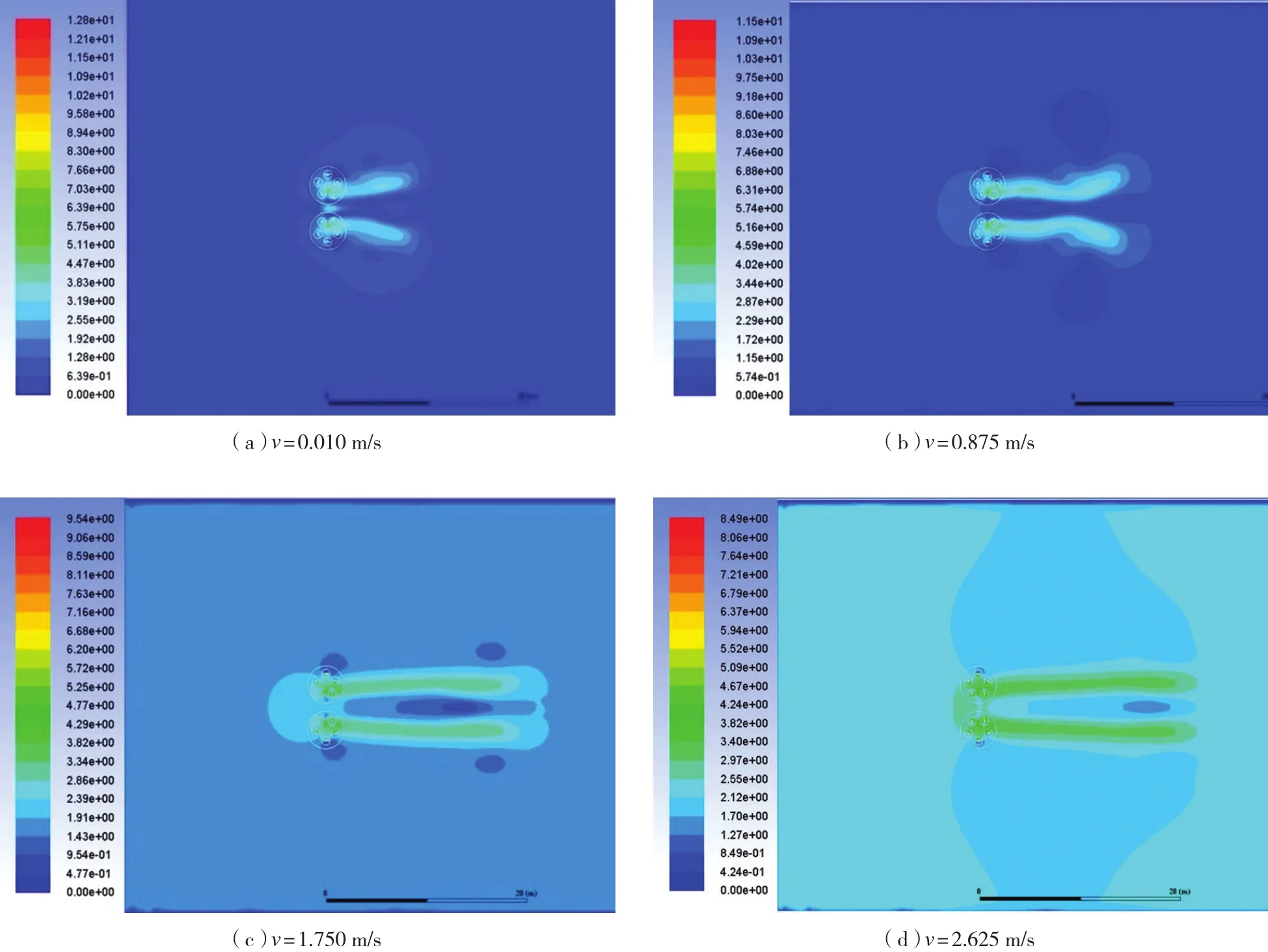
图6 不同进口速度和偏心率下的流场速度云图

在对双推进器CFD仿真结果处理时，取两个推进器的主推力、转矩、输入功率、输出功率和效率的平均值。双推进器水动力参数曲线如下页图7所示，分别为不同偏心率下主推力、转矩、输入功率、输出功率和效率随水流入口速度的变化规律。

对仿真曲线进一步分析可知：

（1）随着水流入口速度增加，主推力和转矩逐渐下降，而输出功率和效率则呈现抛物线趋势。在同一水流入口速度下，偏心率越大，主推力、转矩、输入功率和输出功率越大。

（2）由图7（e）可知，随着入口速度的增加，效率先增大后减小，且增大的速度比减小的速度慢，在入口速度较大时达到最高推进效率点。随着偏心率e的增大，正效率的进速系数范围增大；最高效率点所对应的效率和入口速度随着偏心率的增大而增大；在较低的入口速度时，效率随偏心率的增大而减小。

（3）当偏心率e= 0.8时，推进器的水动力性能参数曲线和其余曲线有差异，这是因为理想状况下的推进器的摆动规律为摆线规律，随着偏心率增大，推进器叶片的角速度变大，当入口速度较小时，推进器叶片的攻角过大从而影响推力。此时，推进器之间的干涉作用超过了其本身由于叶片作摆线运动而对水流的作用，故仿真结果需要排除入口速度在0～0.5 m/s的范围。

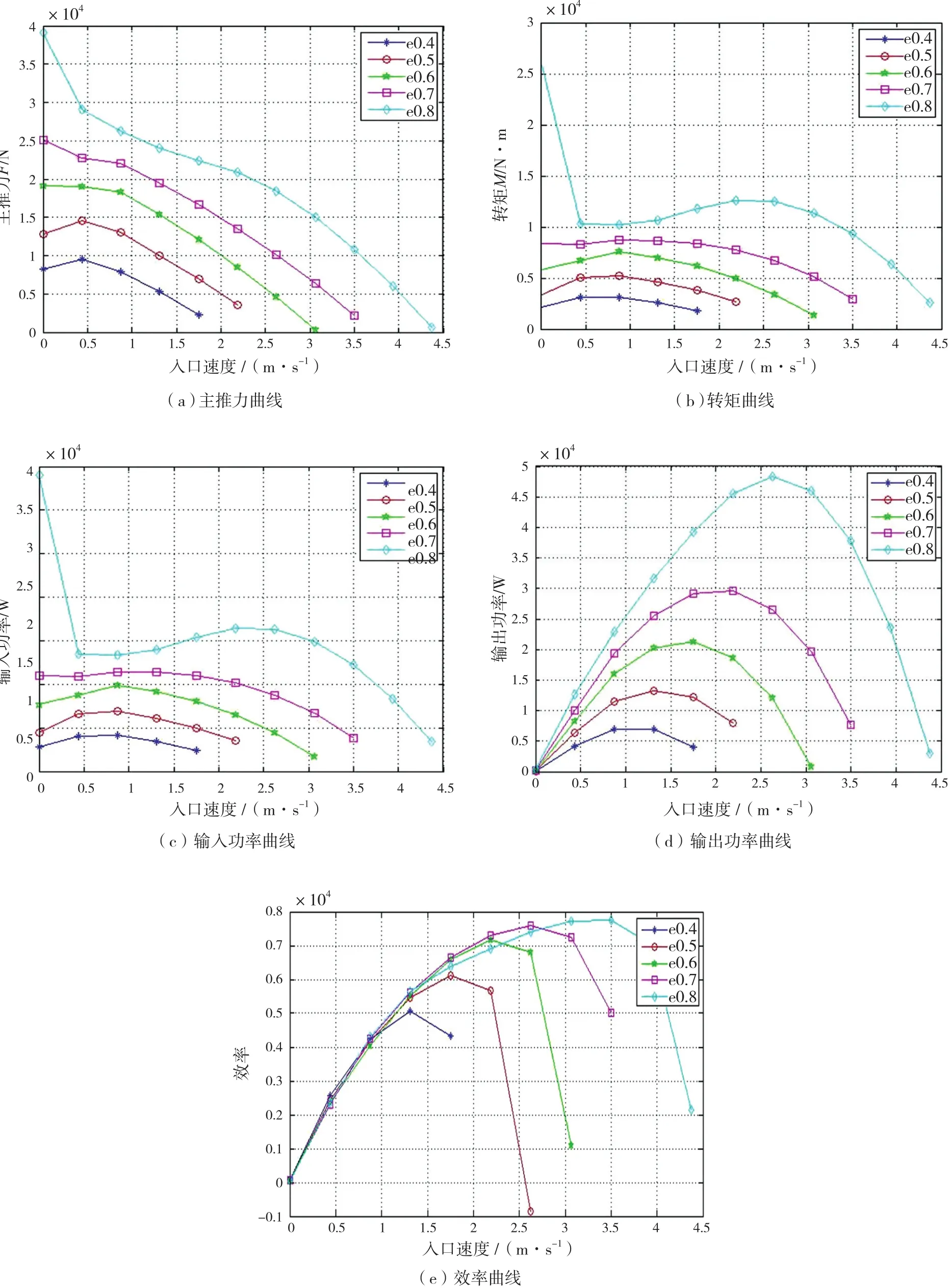
图7 不同速度和偏心率下的双推动器水动力参数曲线

两推进器在实船上安装时，分别向前倾斜3°和向两侧倾斜2°（如图8所示）。因此，当船舶前进时，推进器的位置状态可分解为两部分：第一部分是推进器向两侧倾斜2°，当船舶以一定速度V前进时，在水中的推进器迎面过来的水流速度都是V，故推进器的水动力性能与其是否倾斜无关；第二部分是推进器向前倾斜3°，当船舶以一定速度V ′前进时，实际作用在推进器上的入口水流速度为V，有故倾斜情况下的推进器水动力性能值，只需要将垂直于推进器轴线的速度V转化为船舶速度V ′即可，对于水动力性能影响极其有限。相应地，推进器沿水平方向的推力F ′与垂直于推进器的主推力F的关系有F ′=F·cos 3°，在实船应用中也需进行相应换算。

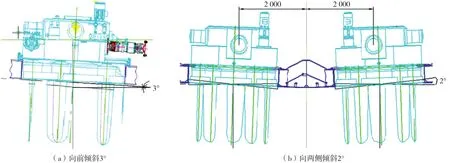
图8 直翼推进器安装位置状态

4 结 语

本文结合实船选用的直翼推进器的型号、安装位置、倾斜角度等多方面因素，通过流场的CFD建模，对推进器的水动力特性进行初步分析，给出了推进器产生的推力、转矩、效率等参数与进口速度及控制点位置之间的关系。

本船在动力定位工况下通过控制直翼推进器实现循迹、定点悬停、艏向保持等功能，在控制过程中需综合考虑电站功率配置等相关输入。本文关于直翼推进器的水动力性能初步分析结论可用于控制策略和算法研究，以实现推力最大化或效率最大化的控制模式，对于动力定位控制的科研开展具有一定的意义，且为后续直翼推进器模拟器的开发及联调试验提供参考依据。