用好几何画板助力数学教学

雷利君

信息技术的发展日新月异，信息处理以及与信息处理有关的技术与教育的结合已日益紧密。各种教育工具软件在商业化推动下也日渐丰富多彩。但数学教师在教学中用得最多的还是office软件下的PPT和WPS（或WORD），而且这些工具仍以静态演示为主。对于教学内容，呈现可代替板书可以节省时间，从而充分利用教学时间进行讲解、讨论、演练等，但若想动态演示各元素在变化中的关系就显功能不足。

几何画板软件既能准确地做出各种静态图形图像，也能动态演示，并且在演示过程中保持图形的性质。更有趣的是，它还有轨迹追踪和动态按钮设置功能，便于师生在教和学中多角度地观察分析问题，是一款不可多得的教学软件。

几何画板能做线型图、弧线型图，包括可控大小的定圆和不定圆、过三点的弧等;还具有平移、旋转、对称等几何变换功能;可绘制各种函数图像。这些功能交叉结合能完成更多与数学有关的任务。几何画板还有丰富的度量功能，线段长度、点的坐标、角度、图形面积均可度量。这使数学学习更接近于实验，更直观，更形象。特别是许多度量结果还可以作为进一步画图的参数来使用，这样一来，所作图形各元素间就可以产生内在的联系。比如，利用點的坐标作为参数，即作为二次函数系数构造二次函数图像，点动其坐标就变，二次函数图像就会随之发生变化，十分有趣！

一、几何画板可以直观形象地演示函数中各常数对图像的影响

如图，在画板中①画出函数x=-10的图像，②在该直线上画点A、K，这两点是可在直线上移动的。③度量点A、K的纵坐标，并分别改标签为a、k。④绘制新函数y=ax2+k。

完成作图后，拖动点A，a的值会随之变化，抛物线开口大小也随之发生改变。而拖动点K，k的值会随之变化，抛物线也会随之上下移动。如下图所示：

1.a值的变化对函数图像的影响：

2.k值的变化对函数图像的影响：

相类似的，我们还可以演示y=a（x-h）2+k的图像随a、h、k值的变化而变化。做法类似，也非常简单。如下图所示：

这样一来，当点的位置改变时坐标改变，二次函数图像也随之发生改变，图像随各系数的变化而变化的情况就一目了然。函数图像动了起来，函数教学也活了起来，学生容易接受，教学轻松愉快。 做好几何画板内容后，还可以嵌入到PPT中，可以做到PPT内容与画板动态演示互为补充，相得益彰。

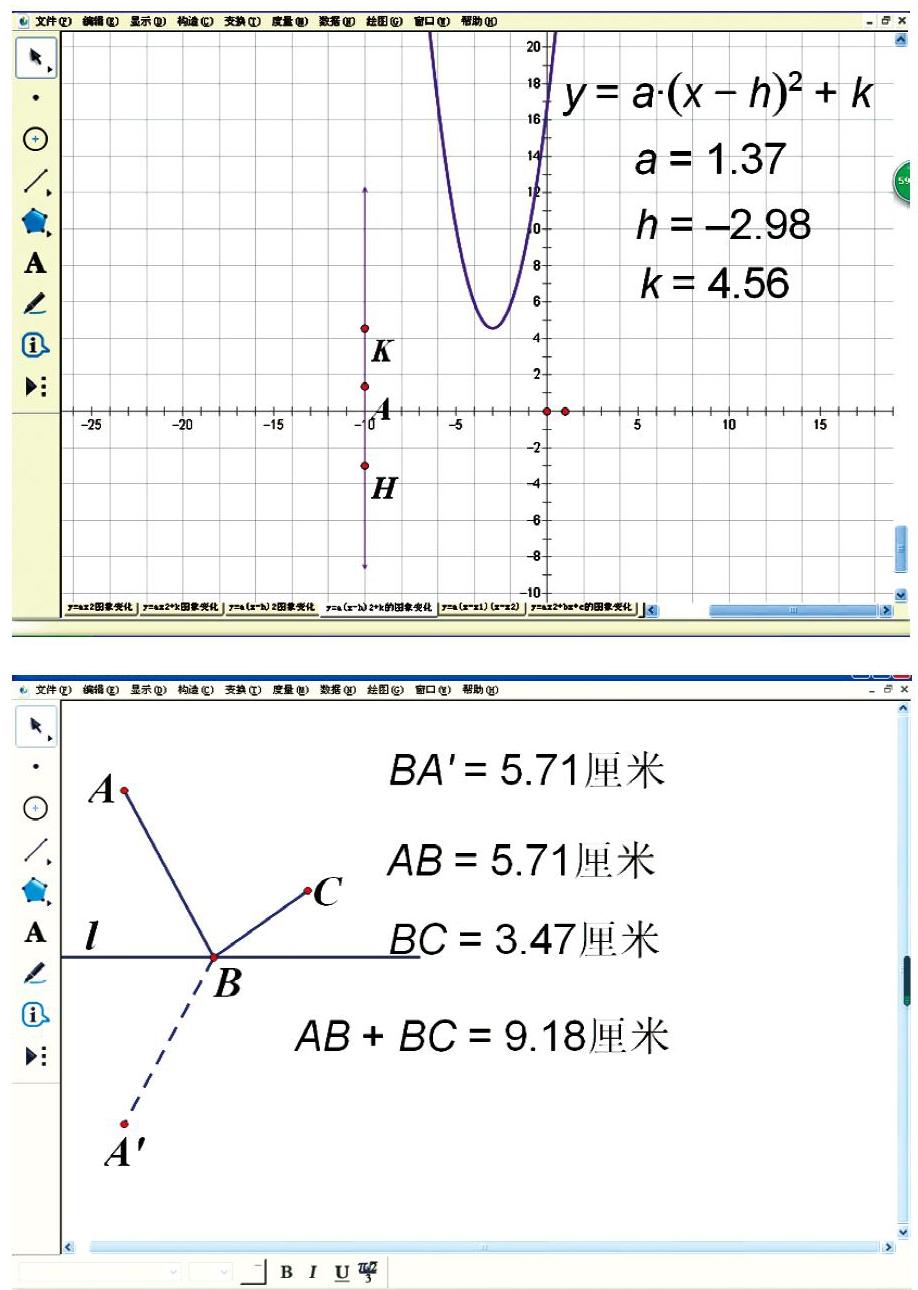
二、利用几何画板的度量和反射功能探究路径最短问题

如图，作点A关于直线l的对称点A?，直线l上的点B，连接AB、BC、A?B。度量AB、BC、A?B的值，计算AB+BC。拖动点B，各度量值和AB+BC值会相应变化。运动中观察点B在什么位置时AB+BC的值最小。这样的运动观察，使抽象的问题形象化了，能帮助学生猜想到点B的位置，从而很容易突破难点。

三、几何画板可以使学生从本质上理解数学概念

如图，在画板中作好轴对称图形，然后拖动其中一个图形观察变化情况;改变对称轴的位置观察变化情况，有利于同学们感性地认识轴对称，从而帮助学生理解“轴对称”的概念。

几何画板还可以帮助师生共同探讨动态问题或在动态中分析疑难问题的解答。其趋向于实验的探究作用使得枯燥的数学学习变得有趣了。由于这一软件安装简单快捷且易学好用，因此，学生也可以在学习中独立使用。