Globally Bounded Solutions in A Chemotaxis Model of Quasilinear Parabolic Type
LIU Bing-chen, DONG Meng-zhen
(College of Science, China University of Petroleum, Qingdao 266580, Shandong Province, P.R. China)
Abstract: In this paper, we consider a quasilinear parabolic-parabolic chemotaxis model with nonlinear diffusivity, aggregation and logistic damping source:where k1epu ≤D(u) or k1up ≤D(u); k2equ ≤S(u) ≤k3equ; g(u) ≤a −beku. It is proved that, if q
Key words:Chemotaxis;Nonlinear Diffusivity;Aggregation;Logistic Type Damping;Globally Bounded Solution
§1. Introduction and Main Results
In this paper, we consider the following parabolic-parabolic Keller-Segel system of chemotaxis
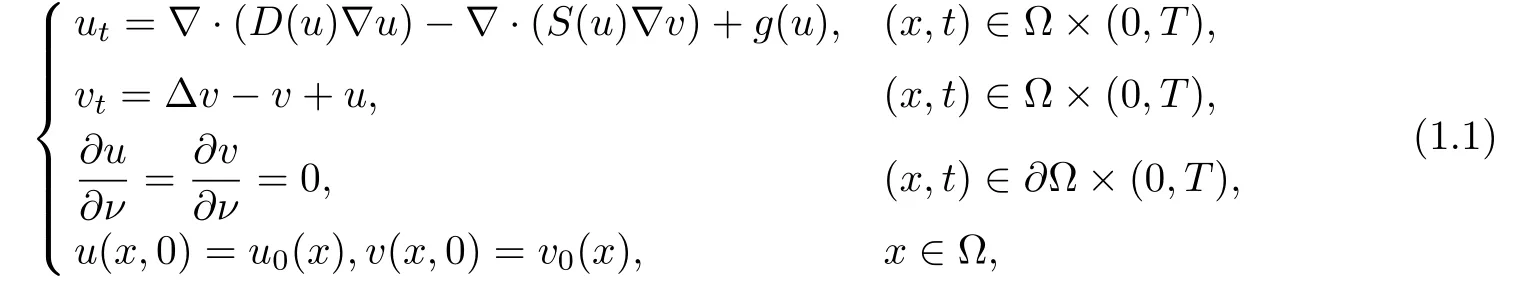
where Ω is a bounded domain in Rn(n ≥1)with smooth boundary ∂Ω;denotes the derivative with respect to the outer normal vector of ∂Ω. The nonlinear diffusivity, the aggregation and the logistic type damping source satisfy that, respectively,
where constants k1,k2,k3>0 and s0>1, and g is smooth on [0,∞) fulfilling that
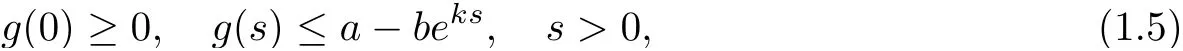
where constant a ≥0, b > 0 and k > 1. The nonnegative initial data of system (1.1) satisfy that
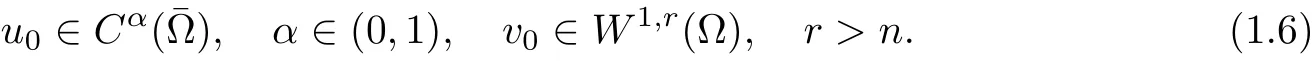
If D(u) ≡1, S(u) = u, and g(u) ≡0, system (1.1) is the classical fully parabolic Keller-Segel model, which characterizes the aggregation process of slime mold under the influence of a chemical substance (see [12]), where the behavior of solutions depends on the interaction between the two mechanisms of diffusion and aggregation, and so a finite time blow-up of u may occur in δ-functional sense under the mass conservation, when the aggregation dominates the system. In the past decades, the classical Keller-Segel system has been extensively studied(see, for example, [2, 3, 5-6, 8, 10-11, 13, 17, 19]).
The quasilinear chemotaxis system (1.1) has vivid biological background. For example, in multicellular organisms, chemotaxis is essential for early development, such as the movement of sperm to the egg during fertilization, and subsequent development stages, such as migration of nerve cells or lymphocytes, and normal functional period. In addition, it is recognized that the chemotaxis of animals in the process of tumor metastasis has been destroyed. The components u and v in system (1.1) represent the density of cells and the concentration of chemoattractant, respectively. The inner source g behaves similarly to the logistic damping source which describes the proliferation and the birth rate versus the death rate of the cells and prevent overcrowding of cells during the process of chemotaxis(see[4, 9, 16]). The functions D and S denote the diffusivity and the chemotactic sensitivity,respectively,depending nonlinearly on u, which are initially introduced by means of volume filling approach (see [9, 18, 22]).Recently, Cie´slak and Winkler in [7], Winkler in [20] studied the global existence and slow grow-up and stabilization of local classical solutions in quasilinear Keller-Segel systems with exponentially decaying diffusivity. The global boundedness of solutions also can be studied by Wang, Hu, Zheng, and Li in [15] for the exponential type diffusivity.
Inspired by the above papers, we want to study the chemotaxis system (1.1) with D,S,g satisfying (1.2)-(1.5), which has not been discussed before. It can be found that the influence of the logistic source is significant in the global boundedness of solutions to the classical Keller-Segel models provided the mass conservation is not in force (see [2, 21, 23-24]). The focus of this paper is on the competing of the nonlinear cross-diffusivity and the logistic type damping in the system (1.1), allowing for rather general choices of D(u), S(u) and g(u). We will study the way of values of k effecting the behavior of classical solutions to system (1.1).
The main result is the following theorem.
Theorem 1.1 If one of the following conditions holds:
(i) q (ii) q =k −1 and b in (1.5) satisfies that b>b0for some constant b0>0, then system (1.1) admits a unique classical solution (u,v) such that Moreover, (u,v) is globally bounded in Ω×(0,∞). The local solvability of system(1.1)can be obtained by standard parabolic regularity theory in a suitable fixed point framework. One can thereby derive a sufficient condition for extensibility of the local solutions (see Lemma 2.1 in [2, 23]). We give the results as preliminaries. Proposition 2.1 Let Ω ⊂Rn(n ≥1)be a domain with smooth boundary. The functions D,S and g satisfy (1.2)-(1.5) with nonnegative initial data (1.6). There exists a constant Tmax∈(0,∞] such that system (1.1) admits a unique solution (u,v), where Moreover, if Tmax<∞, then Now, we deal with the proof of the main result. Since the termused in the key argument of the paper is unsigned,we will make use of the following property as a variation of Maximal Sobolev Regularity (see [3, 23]). Lemma 2.1(Lemma2.2in[23])Consider the following evolutionary problem For each v0∈W2,r(Ω) (r >n) and u ∈Lr((0,T);Lr(Ω)), there exists a unique solution v ∈W1,r((0,T);Lr(Ω))∩Lr((0,T);W2,r(Ω)). Moreover, there exists a constant Cr> 0 such that if s0∈(0,T),v(·,s0) ∈W2,r(Ω) (r > n)with Noticing initial data v0in Lemma 2.1 is required to satisfy the homogeneous Neumann boundary conditions on ∂Ω, we can perform a small time shift to use any positive time as the“initial time” to guarantee such requirement is satisfied naturally. Take s0∈(0,Tmax)∩(0,1).By Proposition 2.1,we have for the local solution that0 on ∂Ω, and there is a constant K >0 such that The proof of Theorem 1.1 is mainly composed of the following two lemmas. At first, we treat the more difficult critical case with q =k −1. Lemma 2.2Under the conditions of Proposition 2.1, if q =k −1, then for any constant β > 0, there exist some constants b0= b0(k,k3,β) > 0 and C = C(a,k,k3,β,u0,v0,|Ω|) > 0 such that ProofMultiplying the first equation of (1.1) by eβu, and then integrating over Ω by parts, we obtain by using (1.2)-(1.5) and Young’s inequality that where constants and k1and k3are defined in (1.3) and (1.4) for any ε > 0 and t ∈(s0,Tmax), respectively.Applying the variation-of-constants formula to (2.2), we have By Lemma 2.1, we know that there exists a constant Ck,β>0 such that Substituting (2.4) into (2.3), we obtain by Proposition 2.1 with (2.1) that with t ∈(s0,Tmax) and Let b0=b0(k,k3,β):=infε>0(2ε+C1Ck,β)>0. Then for any b>b0, we have The proof is complete. Next we will show that the Lβestimate for the case of q Lemma 2.3Under the conditions of Proposition 2.1,if q ProofWithout loss of generality, we suppose β >−q with q ∈R. Due to q with η >0 and Repeating the procedure for the proof of Lemma 2.2 (i.e. (2.2)-(2.4)), we obtain that For any constant b>0, one may choose sufficiently small constants ε,η >0 such that (b −ε −η −ηCk,β)>0. This completes the proof. Finally, we can use the standard Alikakos-Moser iteration in [1] to derive our main results. Proof of Theorem 1.1By a Morse’s iteration procedure(Lemma A.1 in[14]),we claim that there is a constant β0(n,p) > n > 0 which is determined by (A.8)-(A.10) in Lemma A.1 of [14] such that if then there exists a constant C0>0 such that Actually,the estimate(2.5)implies that ∇v is bounded. It is checked that D(u)defined in(1.3)satisfies (A.2) and (A.3) of Lemma A.1 and S(u)∇v satisfies (A.4)–(A.6), respectively. Hence the results in Lemma A.1 hold. It can be checked that (2.5) is ensured by Lemmas 2.2 and 2.3. By using (2.1), we obtain that u is bounded in (0, Tmax). The boundedness of v can be obtain by the standard parabolic regularity. Proposition 2.1 yields that (u,v) must be globally bounded. AcknowledgementThe authors would like to thank the Editors and the anonymous Reviewers for valuable and constructive suggestions improving the first version of this paper. This paper is partially supported by Shandong Provincial Natural Science Foundation,China(ZR2017LA003).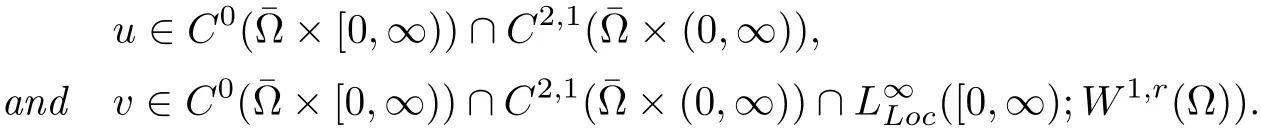
§2. Proof of Theorem 1.1
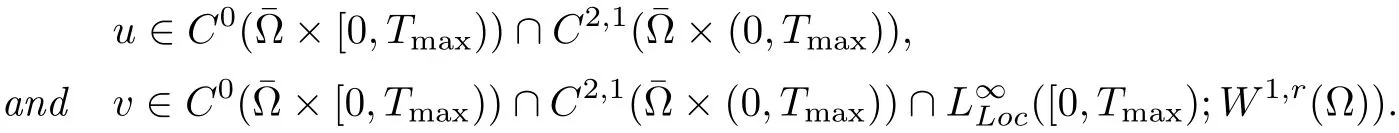
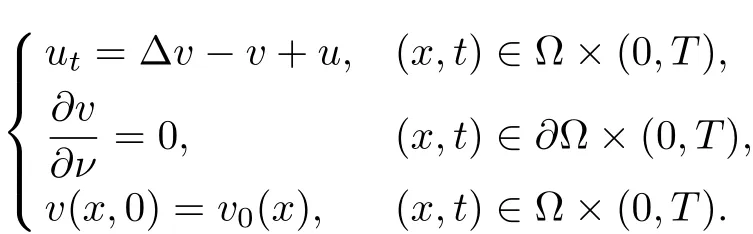
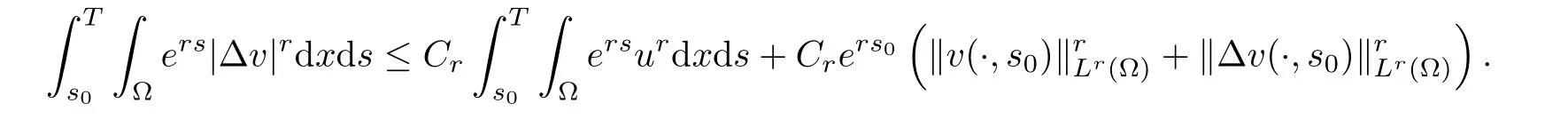
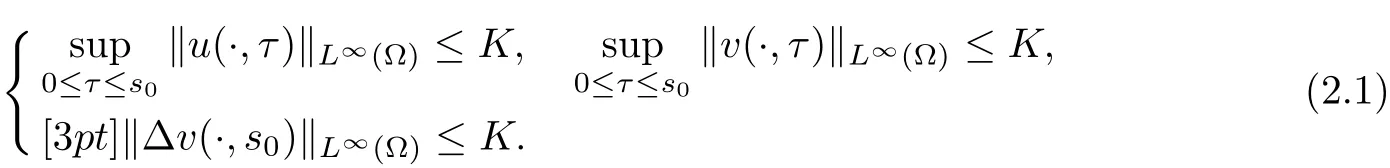
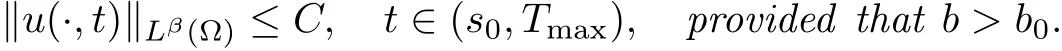

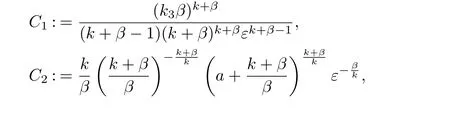
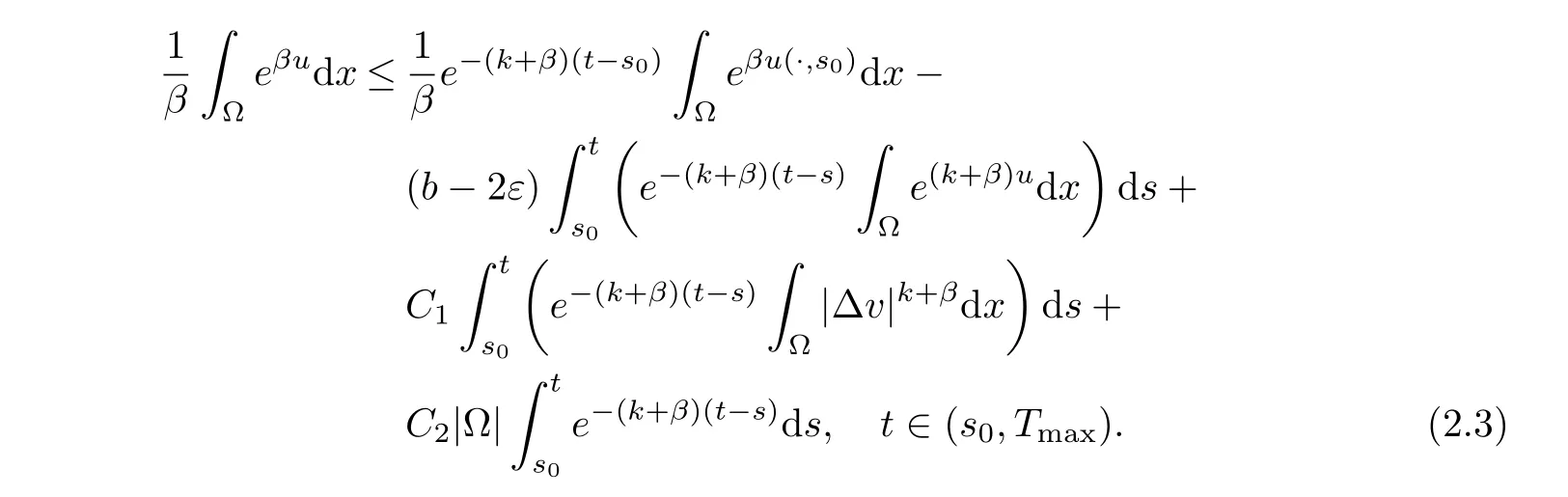
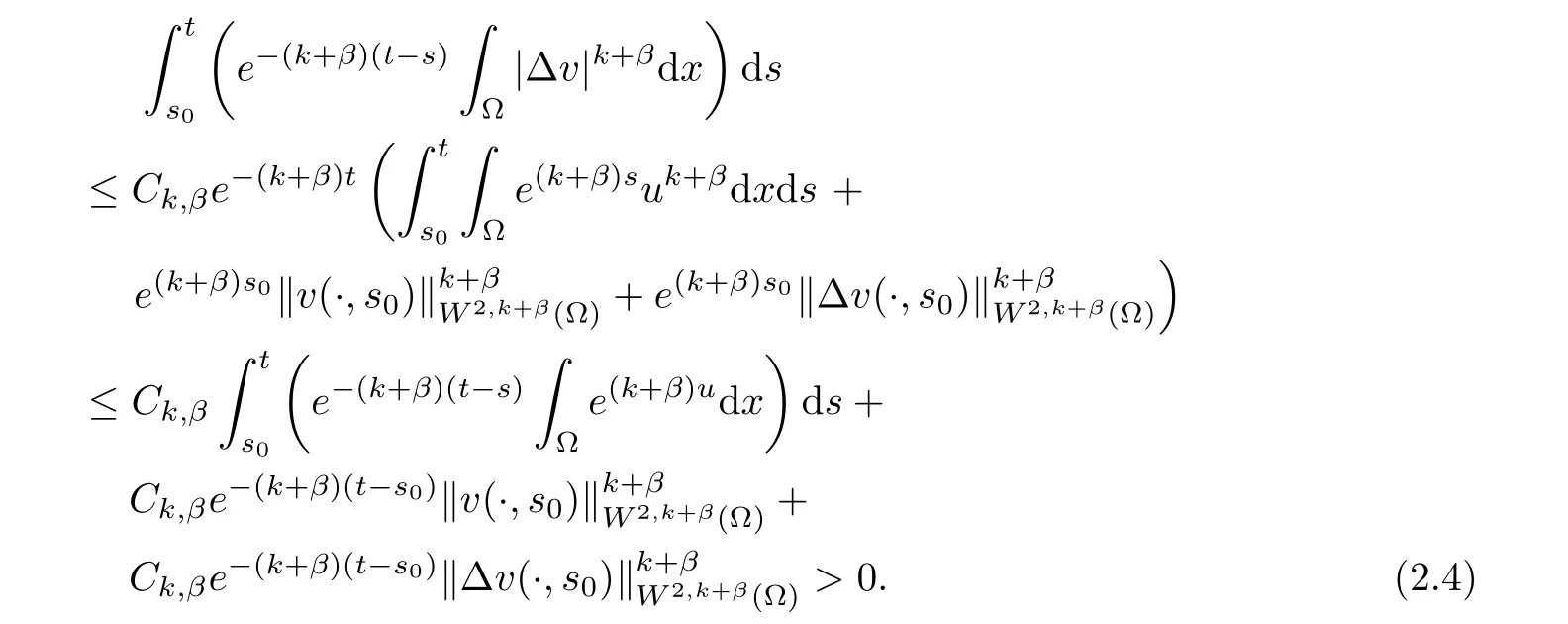
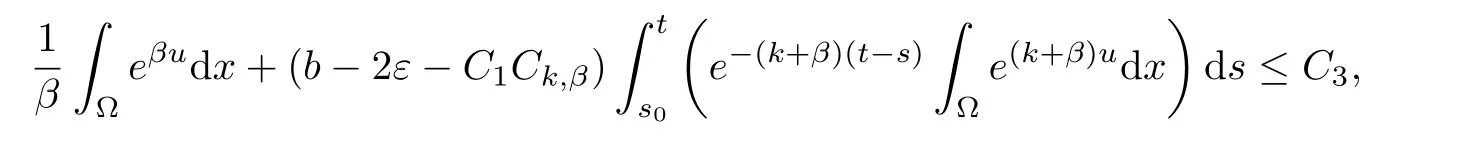


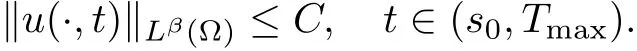
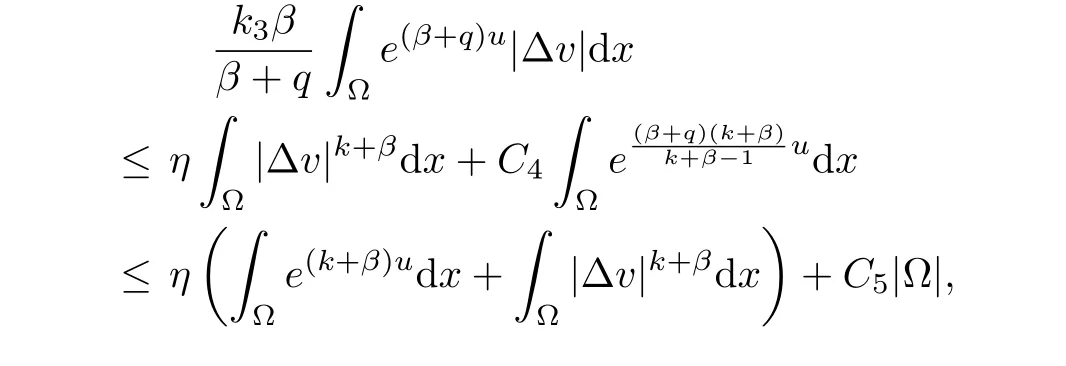
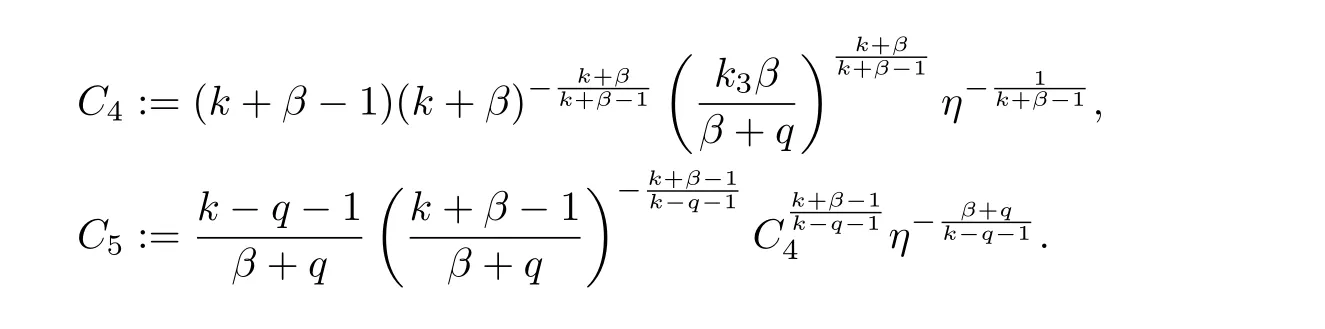
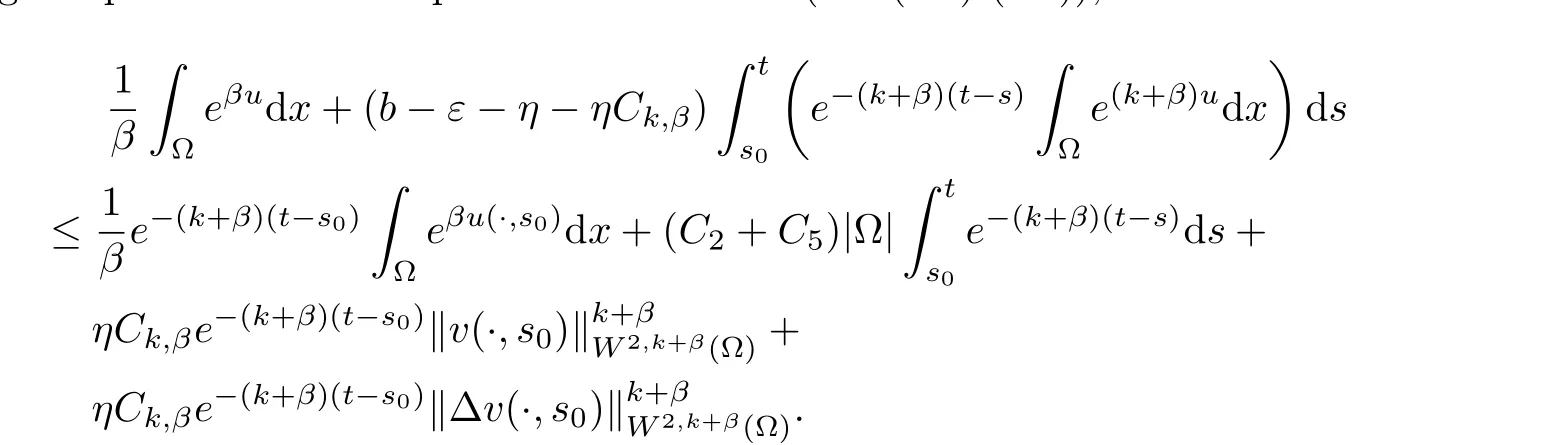
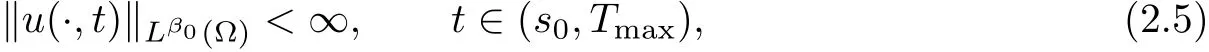
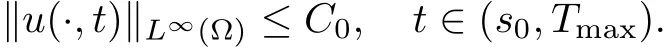
 Chinese Quarterly Journal of Mathematics2019年3期
Chinese Quarterly Journal of Mathematics2019年3期
