Finite Difference Methods for the Time Fractional Advection-diffusion Equation

MA Yan, MUSBAH F. S.

(1.ZhiXing College of Northwest Normal University, Lanzhou 730070, China; 2.Department of Mathematics, University of Bani Walid, Bani Walid 38645, Libya)

Abstract: In this paper, three implicit finite difference methods are developed to solve one dimensional time fractional advection-diffusion equation. The fractional derivative is treated by applying right shifted Gr¨unwald-Letnikov formula of order α ∈(0,1). We investigate the stability analysis by using von Neumann method with mathematical induction and prove that these three proposed methods are unconditionally stable. Numerical results are presented to demonstrate the effectiveness of the schemes mentioned in this paper.

Key words: Time fractional advection-diffusion; Finite difference method; Gr¨unwald-Letnikov formula; Stability; Effectiveness

§1. Introduction

Advection-diffusion equation is a well-known parabolic partial differential equation which describes both spread and movement of a substance or any conserved quantity such as particle,heat,energy,etc.,by a fluid due to the fluid’s bulk motion[1]. The advection-diffusion equation is derived from the Fick’s law with two fluxes: advective and diffusive flux and the conservation law [2].

Fractional partial differential equations can be thought as generalizations of classical partial differential equations, which can give a better description of the complex phenomena such as signal processing, systems identification, control and non-Brownian motion [3] or so called levy motion which is a generalization of Brownian motion [4]. A comprehensive background on this topic can be found in books by [5] and [6].

Fractional advection-diffusion equations (FADEs) are described by a continuous time random walk (CTRW) where the process is defined by non Markovian process, in which the movement of a particle is dependent on past movements [6]. This is the most important feature in fractional models. Many problems in nature can be modelled by fractional advection-diffusion equations,such as those involving ground water fluid flows in a porous medium[7],a movement of solute in an aquifer which can sometimes be related to a Fickian process [8].

Several finite difference approaches for solving FADEs can be found in literature.[4] developed a Lax–Wendroff–type time discretization procedure for spatial fractional advection–diffusion equation. The Riemann–Liouville derivative was used for the fractional term and the dependent function was approximated by using a linear spline to compute the integrals.[9]considered explicit and implicit methods for solving space-fractional advection–diffusion equation with source and variable coefficients. Two finite difference methods were proposed by[7] for solving a space-time fractional advection–diffusion equation in a bounded domain. In this study, the fractional temporal derivative was approximated by using Caputo formula while the fractional spatial derivative was approximated by using the standard and right shifted Gr¨unwald–Letnikov formula. A class of the fractional advection–dispersion equations was discussed by [10]. They studied five models with different intervals of fractional order. The model equation is fractional in space and time, which means it can describe the particle motion in a complex system with heavy tailed and the particle motion with long memory in time. It was pointed out that the proposed methods can be utilized for other kinds of fractional partial differential equations. The fractional Crank-Nicolson method was developed by [11] for solving two-sided fractional advection-diffusion equations. The right shifted Grnwald-Letnikov formula was applied to discretize the two-side fractional derivative term. The same model was also discussed by [12]. They combined the characteristic methods and fractional finite difference methods. A fast and new characteristic finite difference method for two sided fractional advection-diffusion equation was developed by [8]. The method has two features over the standard implicit method in that it is more accurate and efficient. [13] determined the Lie symmetries to reduce a time fractional advection-diffusion equation involving the Riemann-Liouville fractional derivative with a nonlinear source term to a fractional ordinary differential equation. They solved the reduced fractional equation by using Caputo fractional derivative for the fractional part and used implicit second order backward differentiation formula. [14]proposed an efficient and accurate meshless method for solving fractional advection-diffusion equations with variable coefficients. This method is based on moving least square (MLS) approximation. The time fractional derivative is expressed in Caputo sense and approximated by a finite difference scheme of order ((δt)2−α),0 < α ≤1. The spatial derivative was approximated by employing the MLS approach. Crank-Nicolson scheme was discussed by [15] to solve Riesz space fractional advection-dispersion equations. The Riesz fractional derivatives of order α ∈(0,1) and β ∈(1,2] were approximated by using weighted and shifted Gr¨unwald difference operators.

The purpose of this article is to develop three implicit finite difference methods for solving the one-dimensional time fractional advection-diffusion equation:

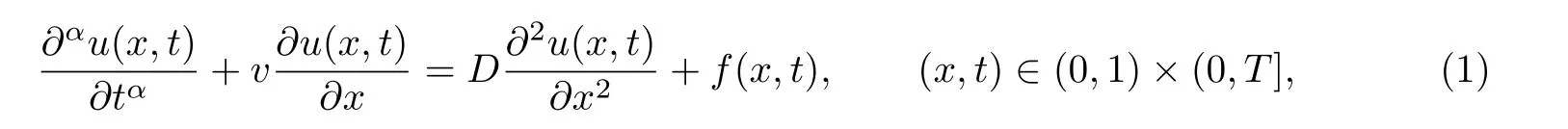
with the initial condition

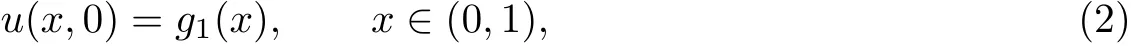
and the boundary conditions

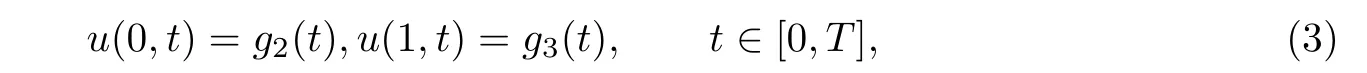
where u(x,t)is a concentration of a quantity such as mass,energy,etc.,v is the average velocity of a quantity,D is the diffusion coefficient (or diffusivity),f,g1,g2and g3are known functions.denotes the Riemann-Liouville fractional derivative. We consider the case when 0<α<1.Note that if α=1, Eq.(1) corresponds to the classical advection diffusion equation.

Regarding he differences between the methods other people conducted and the method developed in our paper as follows: firstly we used Gr¨unwald-Letnikov definition while in other articles Caputo fractional derivative was used for solving time fractional advection-diffusion equations. Both Caputo and Gr¨unwald-Letnikov definition have same order of accuracy. The schemes proposed in our paper can be applied for time fractional advection-diffusion problem that its time fractional part is defined by Caputo fractional derivative taking into account the relation between Riemann-Liouville fractional derivative and Caputo fractional derivative [16].Also, there is no article tried to use an implicit upwind method for solving time fractional advection-diffusion equations to see what kind of solution that gives and compare it with other implicit method. Finally, we have added another kind of example that has nonzero initial condition which was derived from Example 1 to see the result regarding this problem.

Definition 1.1The fractional derivativeof f(t)can be defined by Riemann-Liouville formula as [17]

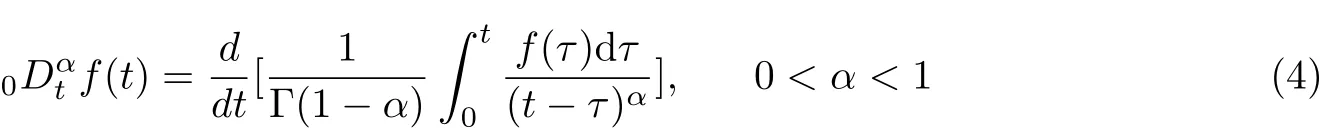
where Γ(·) is the Gamma function and 0 ≤t ≤T.

The above derivative is related to the Riemann-Liouville fractional integral,which is defined as

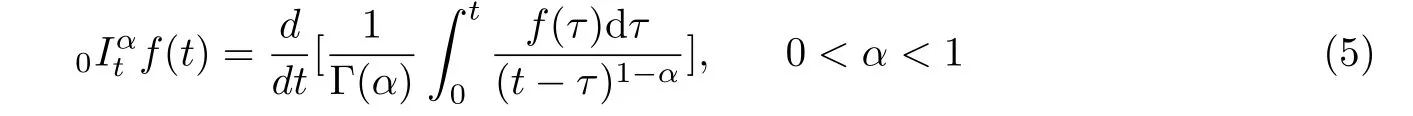
where

Definition 1.2The right-shifted Gr¨unwald-Letnikov formula of function f with respect to independent variable t is defined as [18]

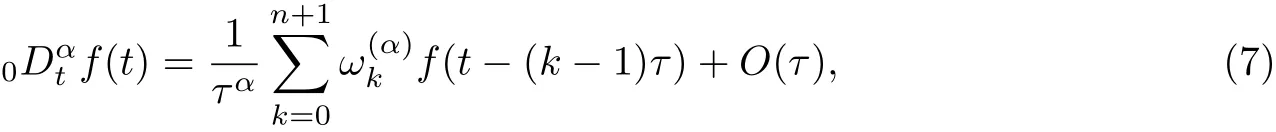
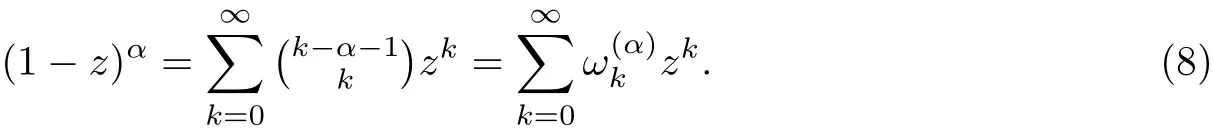
§2. Finite Difference Methods for time Fractional Advection-diffusion Equation

First, we introduce a uniform grid of mesh points (xi,tn), with xi=ih,i=0,1,...,M and tn=nτ, n=0,1,...,N, where M and N are positive integers, h=is the spatial step size in the x direction and τ =is the time step size in the t direction. The notations uniand finare used for the exact values of u and f at the points (xi,tn).

2.1 Implicit backward time central space (BTCS) method

In this section,the implicit BTCS scheme is developed for time fractional advection-diffusion equation (FADE) at time level (n+1) by using right shifted Gr¨unwald-Letnikov formula (7)to discretize the time fractional term of equation (1) and replacing the first and second spatial derivatives by central difference approximations. We set

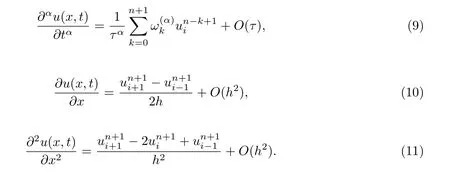
Substitute Eqs.(9),(10) and (11) into Eq.(1) and neglect the truncation error terms, we get

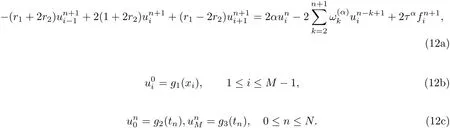
where r1=is the fractional advection number and r2=is the fractional diffusion number.

This scheme is second order accurate in space and has no restriction for choosing the size of the time increment so that it is unconditionally stable.

Note that if the first and second order derivative in space in Eq.(1) are approximated at time level n=0,1,...,N, then the obtained scheme is called forward time central space which is unconditionally unstable for all values of u at D = 0,α = 1 and large values of D and conditionally stable for small values of D0 [19].

2.2 Crank-Nicolson (CN) method

In this method, Eq.(1) is evaluated at the non-grid point (xi,tn+, and set

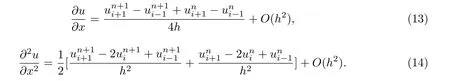
Substitute Eqs.(13),(14) and (9) into Eq.(1) and neglect the truncation error terms, we obtain

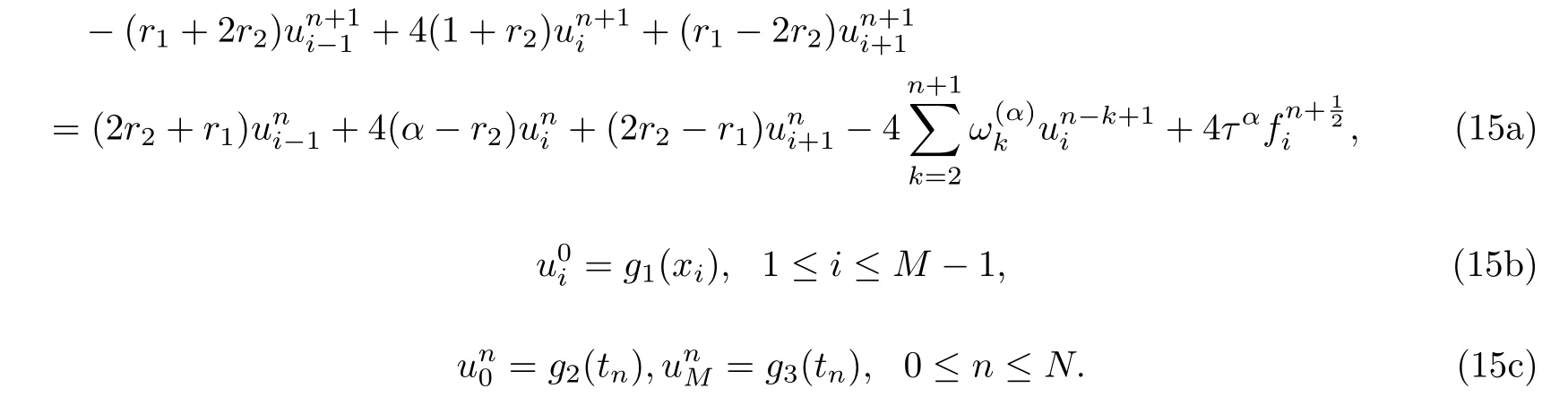
It is well known that the disadvantage of the central difference approximations to the advection diffusion equation is that the numerical solutions under certain condition present spurious node to node oscillations even though the analytical solution is smooth [20]. The ratio of advective to diffusive coefficient is a measure of inadequate resolution [21]. When> 2, the implicit BTCS method (12) and Crank-Nicolson method (15) will contain oscillations. The quantity vh/D is called Peclet number (Pe) in heat flow and Reynold’s number (Re) in fluid[20].

2.3 Implicit upwind method

The two methods that have been considered above for time fractional advection-diffusion equation have symmetric approximation to first order spatial derivative. The estimation of the new implicit upwind method is based on non-symmetric approximation to uxfor the equation(1), so the data can be used only to one side or the other of the discrete point xi. The implicit upwind method at time level (n+1) can be derived. We have

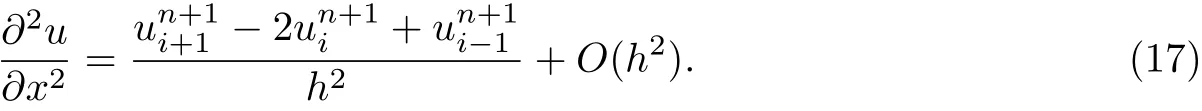
Substitute Eqs.(16),(17) and (9) into Eq.(1) and neglect the truncation error terms, we obtain

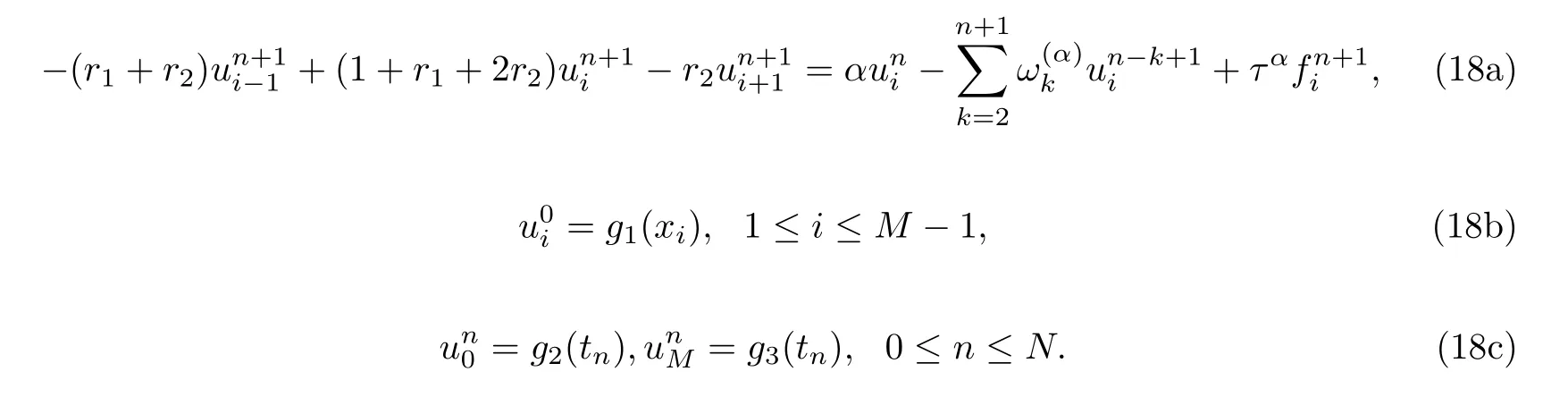
It should be noted that this method have first order in space and time O(τ +h). By using one side approximation to first derivative in space, the implicit upwind method (18) eliminates the nonphysical oscillations even for very complicated multiphase and multicomponent flows[22].

§3. Stability Analysis of Fractional Implicit Finite difference methods

We apply von Neumann method to investigate the stability of these three implicit finite difference methods. The approach of [23] in analyzing the stability of finite difference scheme for a fractional reaction-subdiffusion equation will be used. Let Unibe the approximate solution of the numerical schemes (12), (15) and (18). For simplicity, let us write these equations with no source (homogeneous case). Then Eqs.(12),(15) and (18) become

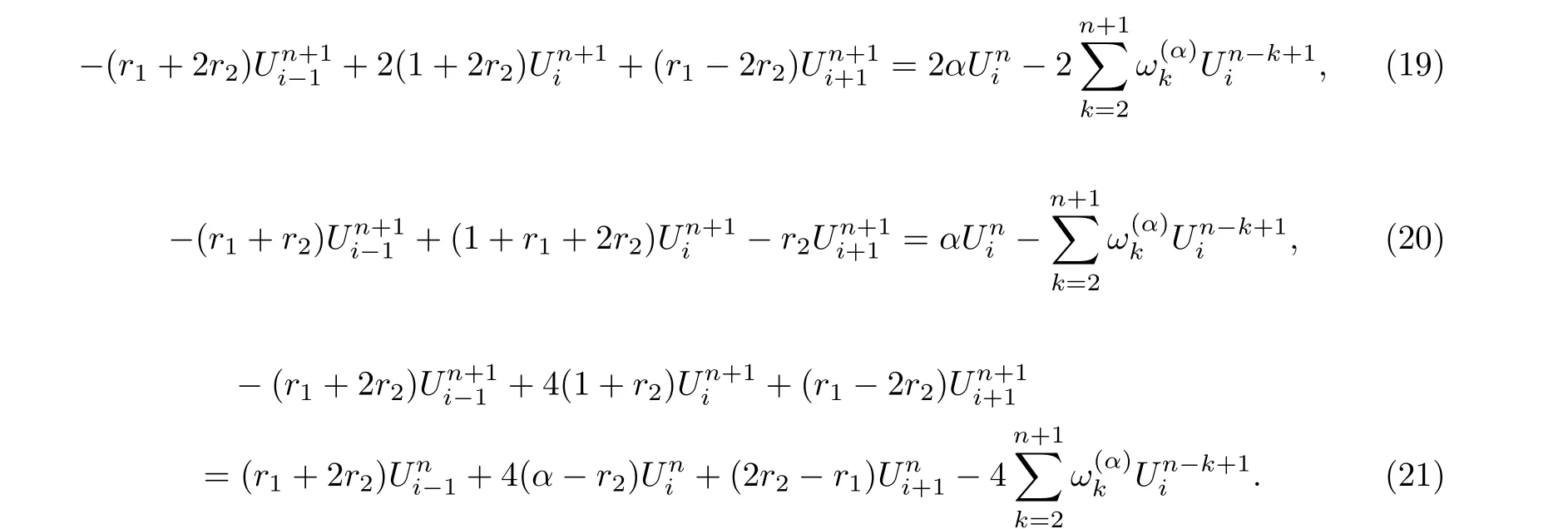
First, we introduce the following Lemma [24].

Lemma 3.1 The coefficients ω(k =0,1,...) satisfy

The round-off error is defined as

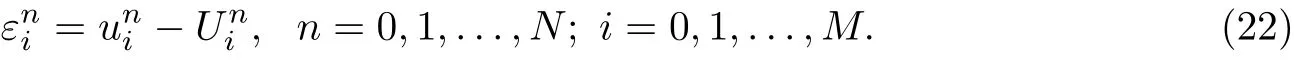
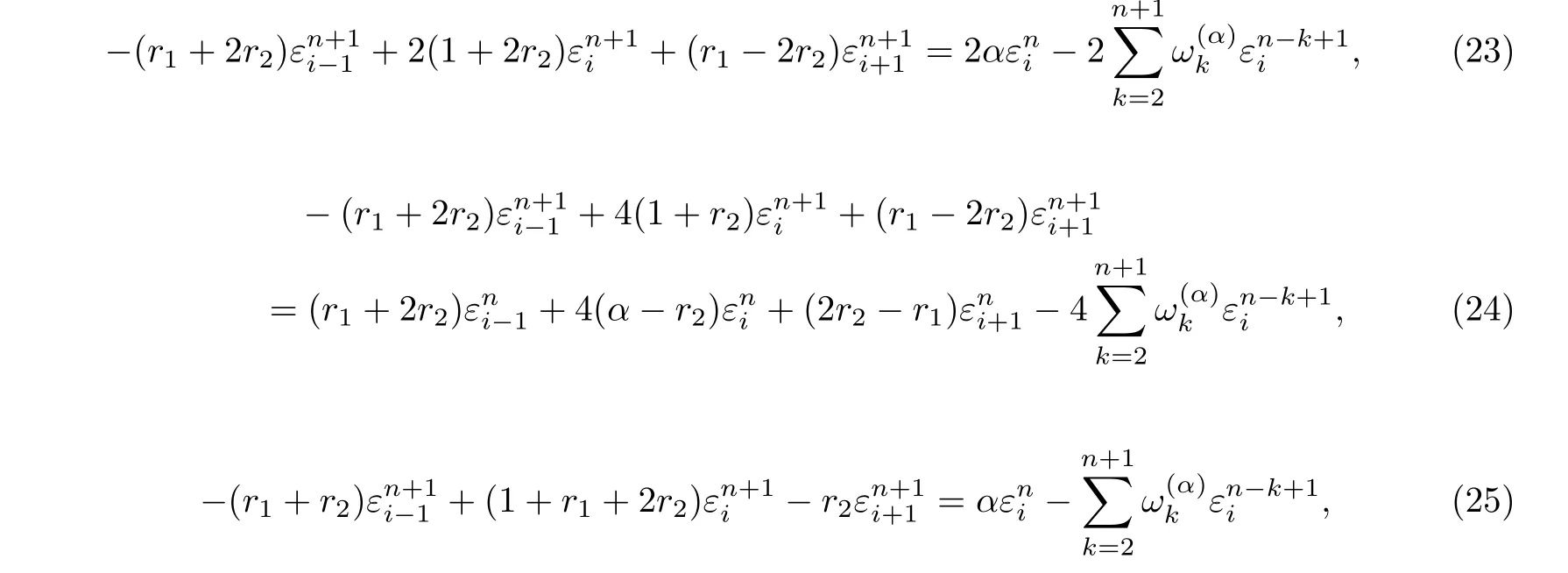
and

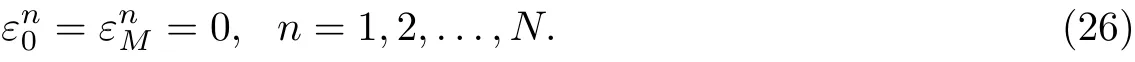
Let us represent the error function ε(ih)=εi,i=0,1,...,M of an initial value as a Fourier series [25]

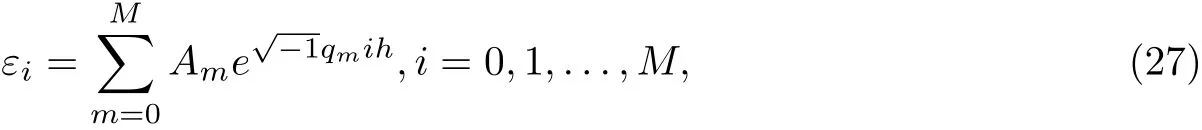
where qm=and L is the interval of the function.

To study the propagation of error as time increases, let us omit the summation and the constant Amand take only a single termwhere

To measure the magnitude of the error vectorn=0,1,...,N,we introduce the discrete l2norm

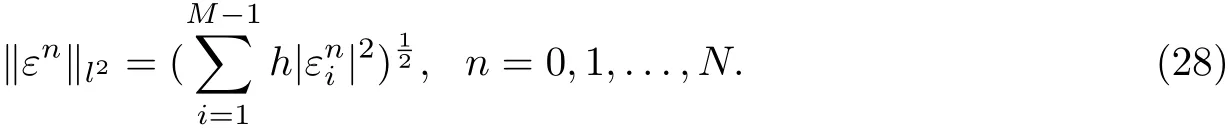
For the continuous function,the l2norm is given by integrals over[0,1]instead of sums over the vector elements [26]

Suppose the solution of equations (23)-(26) is in the form

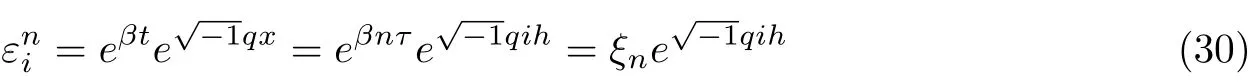
where ξn= eβnτis termed the temporal or amplification factor and β is complex temporal number which depends upon q.

It can be easily seen that at n=0, the solution reduces toand ξ0=1.

3.1 Stability analysis of the implicit backward time central space method

Substituting Eq.(30) into Eq.(23) and using the identity

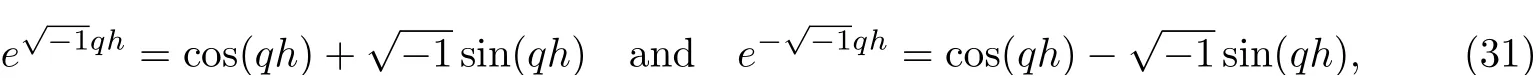
we get

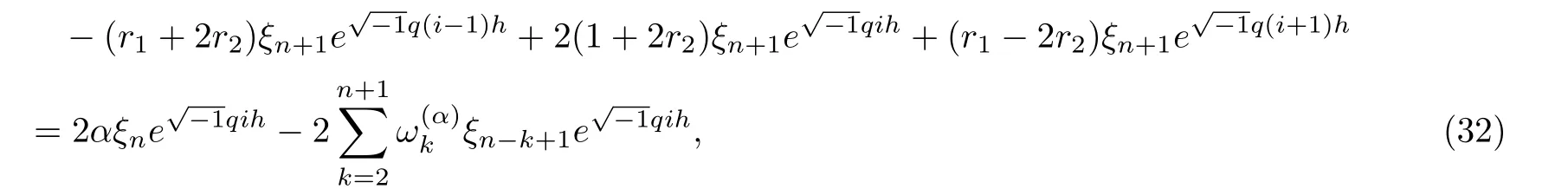
which can be reduced to

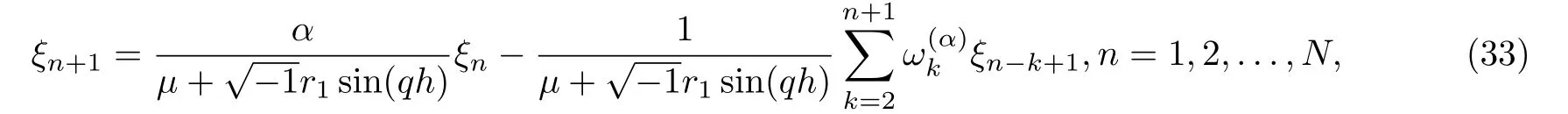
where µ=1+4r2sin2

Proposition 3.1Assuming that ξn+1(n = 0,1,...,N) is the solution of equation(33),then we have |ξn+1|≤|ξ0|, n=0,1,...,N.

ProofWe use the mathematical induction for the proof as in[23]. From Eq.(33)at n=0,then

and

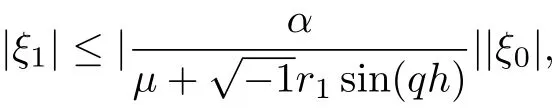
and it follows that

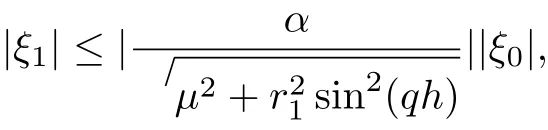
Since µ≥0 and 0<α<1, then |ξ1|≤|ξ0|.

Now suppose that |ξm+1|≤|ξ0|,m=0,1,...,n,using Lemma 3.1 and from Eq.(33), we get

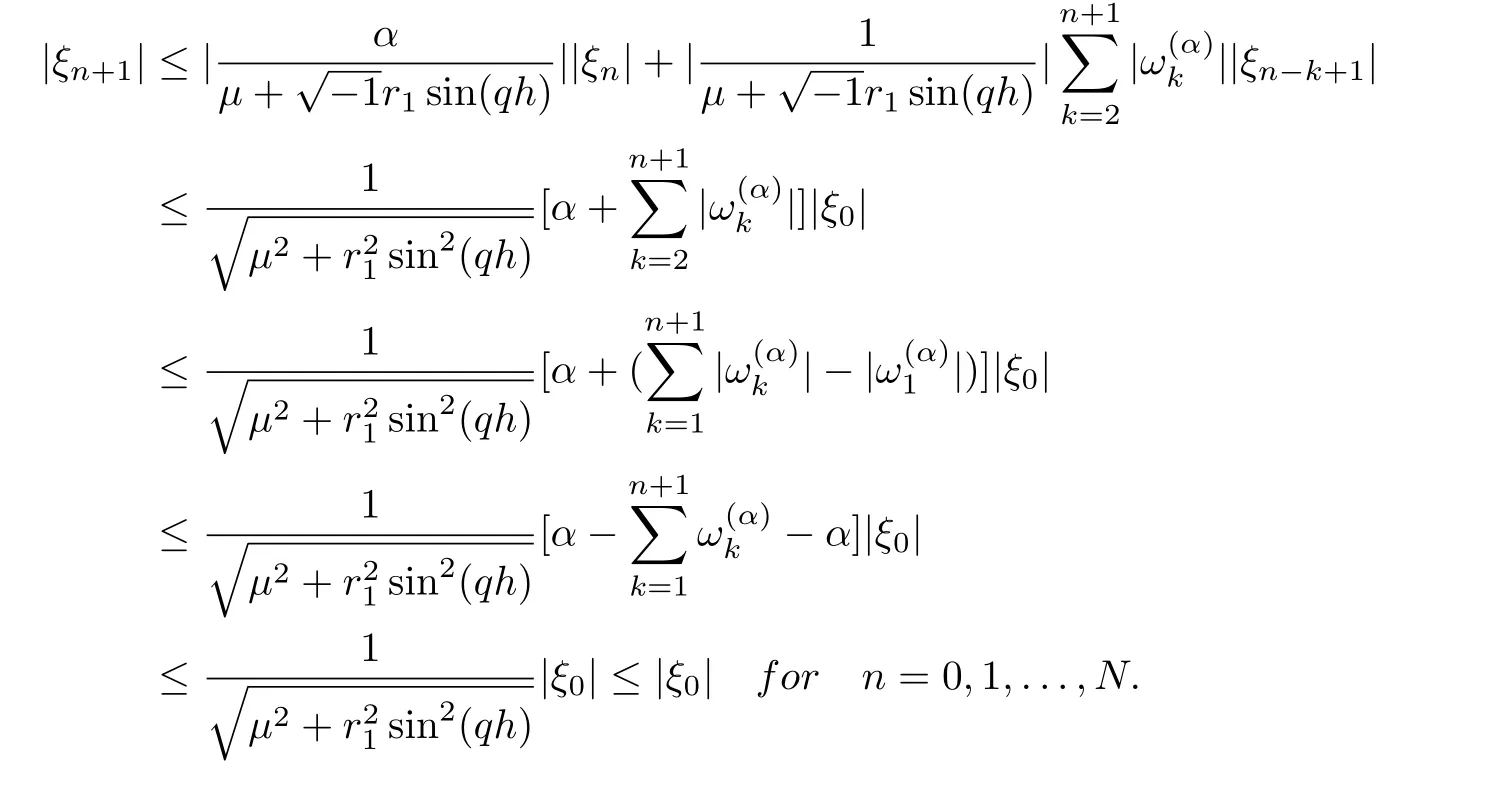
Proposition 3.2The implicit backward time central space scheme(12) for the time fractional advection-diffusion equation is unconditionally stable.

ProofFrom (28) and Proposition 3.1, then, n=0,1,...,N.

This completes the proof.

3.2 Stability analysis of the Crank-Nicolson method

Substituting Eq.(30) into Eq.(24) gives

Simplifying Eq.(35), we get

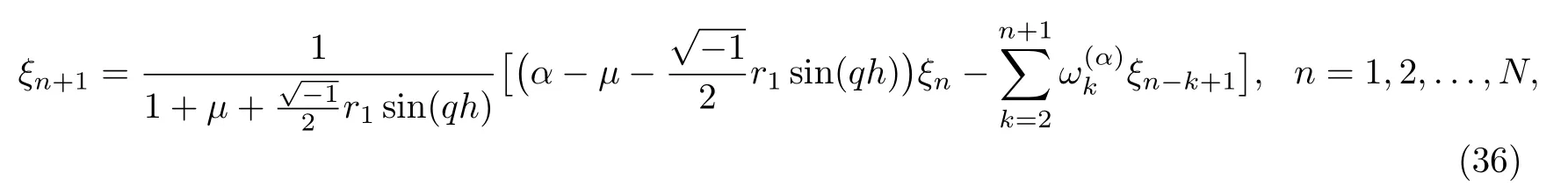
where µ=2r2sin2

Proposition 3.3If ξn+1(n=0,1,...,N)satisfy the equation(36),then we have|ξn+1|≤|ξ0|, n=0,1,...,N.

ProofBegin with n=0 from Eq.(36),we have

then

Since the maximum value of sin= 1, then |ξ1| ≤for all values of r2>0 and 0<α<1.

Now suppose that|ξm|≤|ξ0|,m=1,2,...,n,using Lemma 3.1 and from Eq.(36),we obtain at the maximum value of sin(1, we have

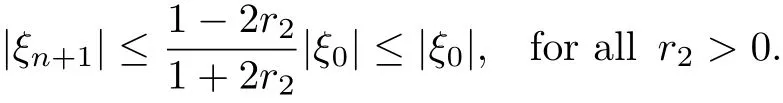
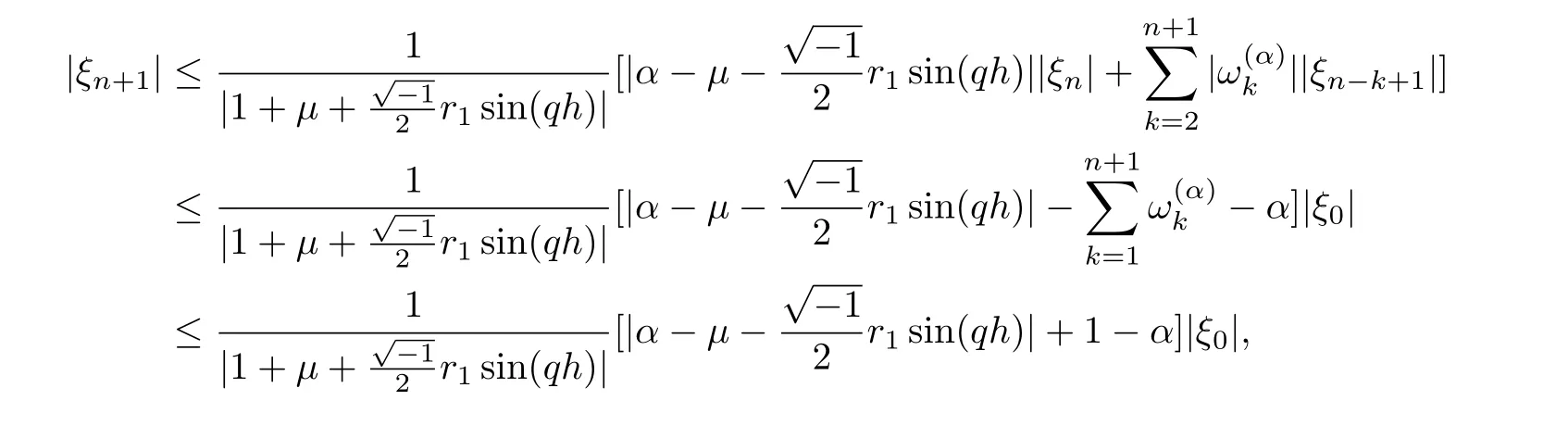
This completes the proof.

Proposition 3.4The Crank-Nicolson(CN)scheme(15)for the time fractional advectiondiffusion equation is unconditionally stable.

ProofFrom (28) and Proposition 3.3, thenn=0,1,...,N.

This completes the proof.

3.3 Stability analysis of the implicit upwind method

Substituting Eq.(30) into (25) gives

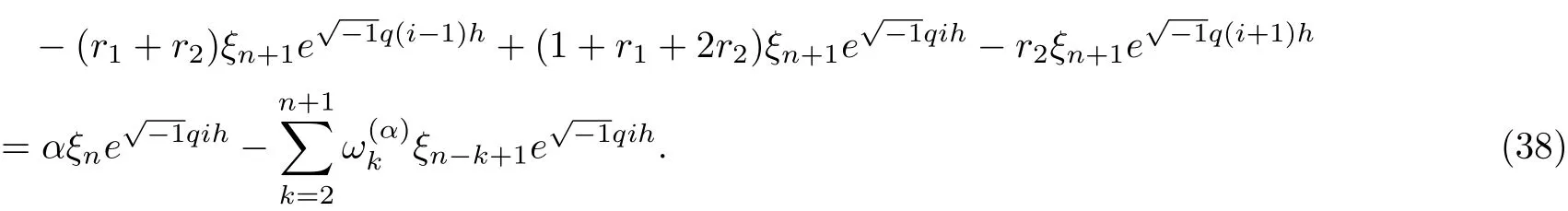
Simplifying Eq.(38) once,we get

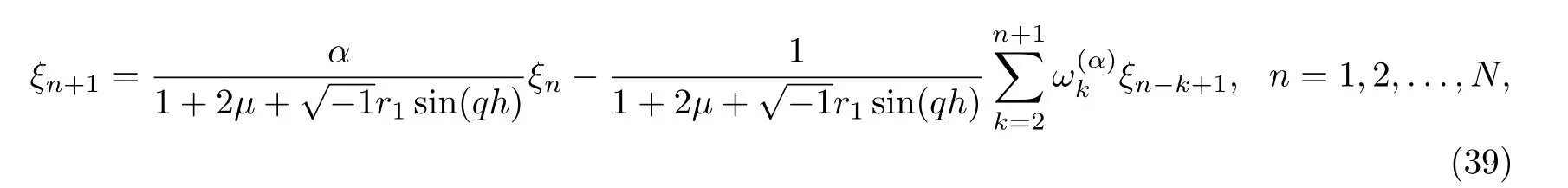
where µ=r1sin2+2r2sin2

Proposition 3.5If ξn+1(n=0,1,...,N) is the solution of equation (39), then we have

ProofAt n=0 from Eq.(39), we have

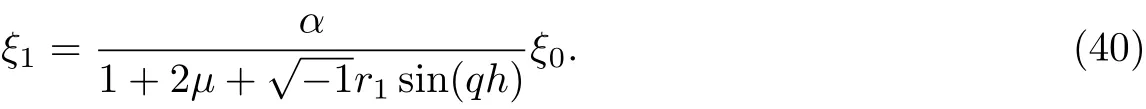
Since µ≥0 and 0<α<1 then

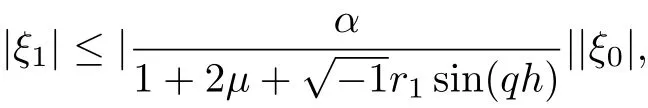
and

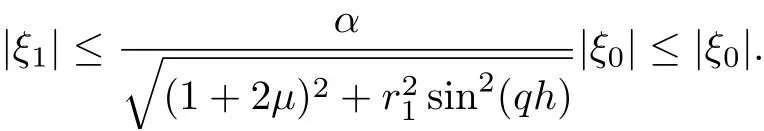
Now suppose that |ξm+1| ≤|ξ0|,m = 0,1,...,n, using Lemma 3.1 and from Eq.(39), we obtain

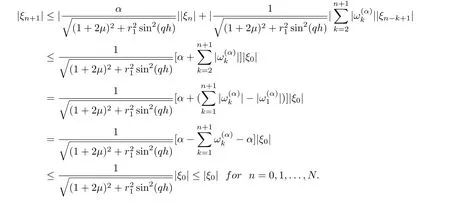
Proposition 3.6The implicit upwind scheme(18) for the time fractional advectiondiffusion equation is unconditionally stable.

ProofFrom (28) and Proposition 3.5, then

This completes the proof.

§4. Numerical Experiments

In this section, we present some numerical results to confirm our theoretical analysis.

Example 4.1Let us consider the equation from [27]

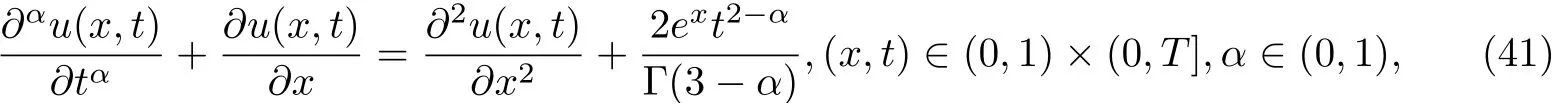
with the initial condition

and the boundary conditions

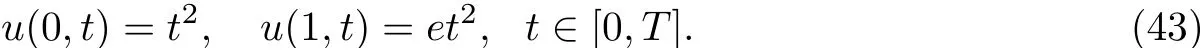
The exact solution of Eqs.(41)-(43) is

We choose α = 0.5. The three numerical methods discussed in this paper for solving the above example are implemented and their solutions are compared with the exact solution. Fig.4.1 illustrates the numerical results of the proposed methods and the exact solution.

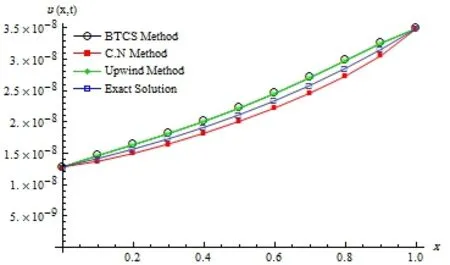
Fig.4.1 Comparison between the results of BTCS, CN, upwind and the exact solution at τ =1.3379×10−5 and h=0.1.

The results of the errors of BTCS, CN and upwind method for time fractional advectiondiffusion problem in discrete l∞and l2norm are listed respectively in table 4.1, 4.2 and 4.3 together with the order of convergence. We first take h = τ =and then decrease the mesh size of h to the half and τ to. The maximum error and l2error are evaluated by the following formulas [24]

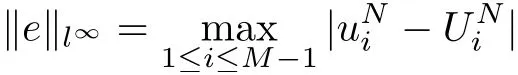
and

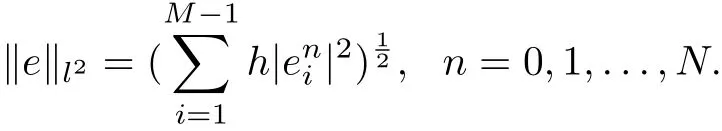
The order of convergence r(τ,h) is evaluated by the following formula

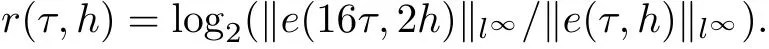
From the tables 4.1-4.3, it can be seen that the numerical methods are straight forward and in good agreement with the analytical solution. It should be noted that although the implicit CN and BTCS method have a truncation error of second order in space and first order in time,the CN method produced slightly more accurate results than the implicit BTCS due to the half time step derivation of the CN method. The implicit upwind method has the truncation error of the order O(τ +h), so that it is slightly less accurate than the implicit BTCS method.

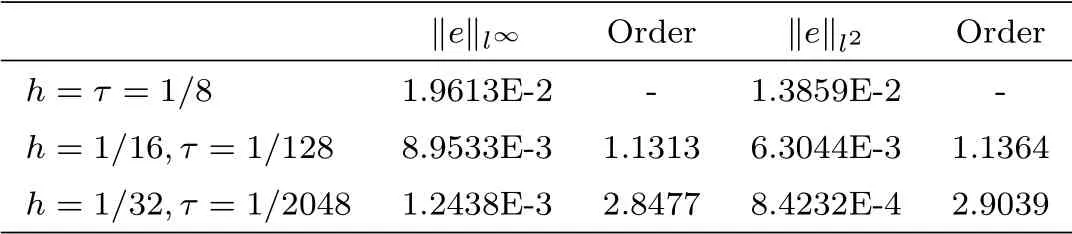
Table 4.1 Errors and order of convergence of BTCS method at α=0.5.

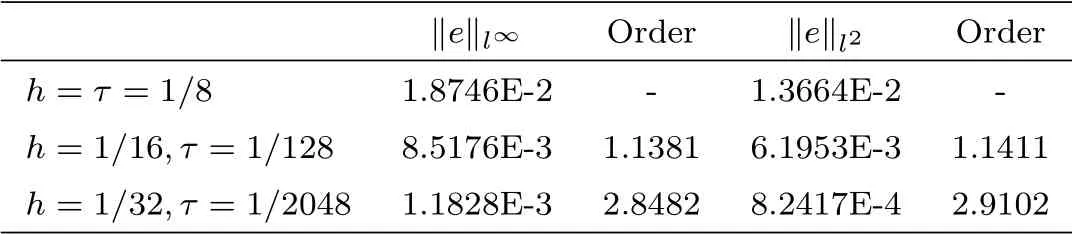
Table 4.2 Errors and order of convergence of CN method at α=0.5.

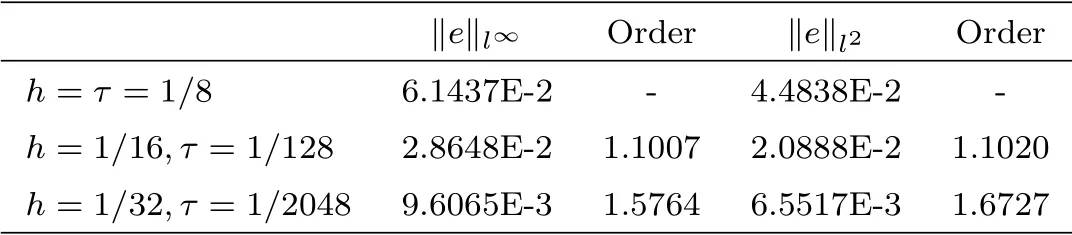
Table 4.3 Errors and order of convergence of upwind method at α=0.5.

Example 4.2Consider the time fractional advection-diffusion problem in Example 4.1 with nonzero initial condition, taking into consideration that the temporal fractional derivative term here is defined by the Riemann-Liouville derivative definition (4) at t ∈(a,T]. Then the problem is defined as

with nonzero initial condition

and the boundary conditions

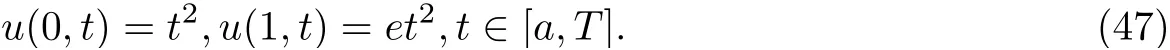
A comparison of the exact values of u, the computed values using BTCS, CN and upwind method are shown in figure 4.2 at different values of a. It can be seen that the accuracy of numerical results of the methods decreases as the values of a decreases. This is due to the rounding error and the number of arithmetic operations that increase when the initial value of time becomes smaller for this problem and parameter values considered.

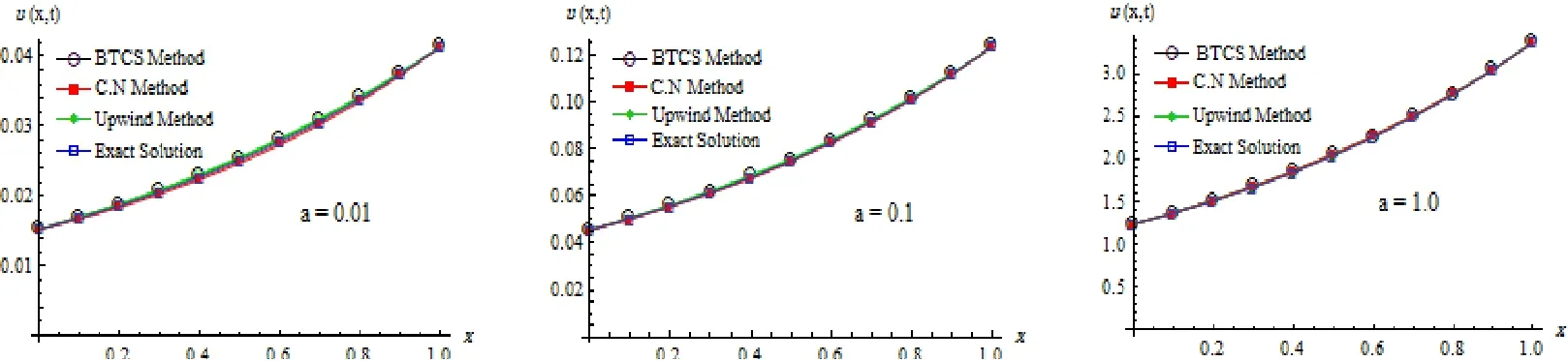
Fig.4.2 Comparison between the results of BTCS, CN, upwind and the exact solution at τ =1.3379×10−2,h=0.1 and α=0.5.

§5. Conclusion

Three implicit finite difference methods were introduced in this article to solve one dimensional time fractional advection-diffusion equation. The methods are unconditionally stable.

The comparison between the methods is made and tested against the analytical solution. It should be noted that the proposed algorithms produced reasonable results and can be applied to solve other kind of fractional advection-diffusion equations(i.e. fractional in space or fractional in time and space).