Algorithm on the Optimal Vertex-Distinguishing Total Coloring of mC9
HE Yu-ping, CHEN Xiang’en
(College of Mathematics and Statistics, Northwest Normal University, Lanzhou 730070, P. R. China)
Abstract: Let G be a simple graph and f be a proper total coloring (or a total coloring in brief)of G. For any vertex u in G,Cf(u)denote the set of colors of vertex u and edges which incident with vertex u. Cf(u)is said to be the color set of vertex u under f. If Cf(u)Cf(v)for any two distinct vertices u and v of G,then f is called vertex-distinguishing total coloring of G (in brief VDTC), a vertex distinguishing total coloring using k colors is called k-vertexdistinguishing total coloring of G (in brief k-VDTC). The minimum number k for which there exists a k-vertex-distinguishing total coloring of G is called the vertex-distinguishing total chromatic number of G, denoted by χvt(G). By the method of prior distributing the color sets, we obtain vertex-distinguishing total chromatic number of mC9 in this paper.
Key words: the union of graphs; proper total coloring; vertex-distinguishing total coloring;vertex-distinguishing total chromatic number
§1. Introduction
With coloring problem of graphs is widely applied in reality, it has gradually become one of important fields which were studied by many scholars. The vertex-distinguishing proper edge coloring was discussed in [1-4].
Let G be a simple graph and let f be a proper total coloring of G. For any vertex u in G,Cf(u) denote the set of colors of vertex u and edges which incident with vertex u. Cf(u) is said to be the color set of vertex u under f. If Cf(u)Cf(v) for any two distinct vertices u and v of G, then f is called vertex-distinguishing total coloring of G (in brief VDTC), a vertex distinguishing total coloring using k colors is called k-vertex-distinguishing total coloring of G(in brief k-VDTC). The minimum number k for which there exists a k-vertex-distinguishing total coloring of G is called the vertex-distinguishing total chromatic number of G, denoted by χvt(G). That is, χvt(G)=min { k | G has a k-VDTC}.
For a graph G, let ni(G) denote the number of vertices of degree i. Set
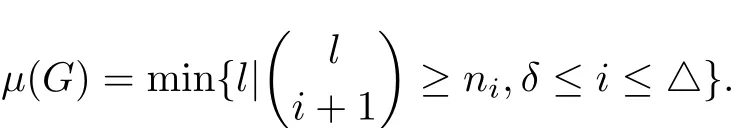
Obviously, χvt(G)≥µ(G).
Vertex distinguishing (proper) total coloring of a graph is introduced by Zhang et al in[5]. The vertex distinguishing total chromatic numbers of complete graph, complete bipartite graph, wheel, fan, double star, cycle, path, Pn∨Pn, Pn∨Cn, Cn∨Cn, etc, are determined and the following conjecture were proposed in [5].
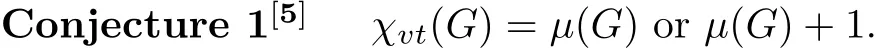
The vertex-distinguishing total chromatic numbers of 2Cn, mC3, mC4, mC5and mC7have been discussed in [6-10]. The vertex-distinguishing total chromatic number of the union mC9of m disjoint cycles of order 9 will be discussed and give the following Theorem 1. Its proof is obtained by the algorithm on the optimal vertex-distinguishing total coloring of mC9given in Section 4.

The vertex-distinguishing VE and IE-total colorings of graphs were discussed in [11, 12].
§2. Preliminaries
Firstly, for each n ≥3, we construct an (n −2)×(n −2) square matrix Anas follows.
The first row of Anis ( {n,1,2},{n,2,3},{n,3,4},··· ,{n,n −3,n −2},{n,n −2,n −1} );
The second row of Anis ( {n,1,3},{n,2,4},{n,3,5},··· ,{n,n −3,n −1},∅);
The third row of Anis ( {n,1,4},{n,2,5},{n,3,6},··· ,∅,∅);
······
The (n −3)-th row of Anis ( {n,1,n −2},{n,2,n −1},∅,··· ,∅,∅);
The (n −2)-th row of Anis ( {n,1,n −1},∅,∅,··· ,∅,∅).
Note that each element of Anis either an empty set or a 3-subset of {1,2,··· ,n}, which contains n.
Let 1 ≤i1 Submatrix An[i1,i2,··· ,ir|j1,j2,··· ,js] of Anis an r×s matrix which is comprised by all the elements of Anin i1-, i2-, ···, or ir-th rows and in j1-, j2-, ···, or js-th columns of An. If elements in a 9×2 submatrix B of Anare exactly the color sets of all vertices of 2C9under some its vertex-distinguishing proper total coloring, then a submatrix B is called good. If nine elements(not empty set)of Anare exactly the color sets of all vertices of one C9under some its vertex-distinguishing proper total coloring, then the group which consists of the nine elements is called good. Nnie elements in a good 9×2 submatrix of Anmay become a good group,but nine elements in a good group are not necessarily the elements of a good 9×2 submatrix of An. The total coloring of C9is shown in Fig. 1,we denote it by f(c1,c2,c3,c4,c5,c6,c7,c8,c9,c10,c11,c12,c13,c14,c15,c16,c17,c18). Fig. 1: VDTC f(c1,c2,c3,c4,c5,c6,c7,c8,c9,c10,c11,c12,c13,c14c15,c16,c17,c18) of C9 Lemma 1When i ≡1(mod 9),j ≡1(mod 2),if all elements in An[i,i+1,i+2,i+3,i+4,i+5,i+6,i+7,i+8|j,j+1]are not empty sets,then An[i,i+1,i+2,i+3,i+4,i+5,i+6,i+7,i+8|j,j+1] is a good 9×2 submatrix. ProofNote that Obviously,eighteen subsets in the first and second columns of An[i,i+1,i+2,i+3,i+4,i+5,i+6,i+7,i+8|j,j+1] are the color sets of all vertices of 2C9under vertex-distinguishing total coloring f(j,n,j+i,j+i+1,n,j+i+2,j+1,j+i+3,n,j+i+4,j+1,j+i+5,n,j+i+6,j+1,j+i+7,n,j+i+1) and f(j,j+i+2,n,j+i+3,j,j+i+4,n,j+i+5,j,j+i+6,n,j+i+9,j+1,n,j+i+8,j,n,j+i+7). The proof is completed. If an element of Anis neither element of any good 9×2 submatrix appeared in Lemma 1 nor an empty set, then the element of Anis called the element left of An. Lemma 2If n ≡0,3,6(mod 9),n ≥3, then all nonempty elements of Anexcept for{n,1,n −1} can be partitioned intogroups, such that each group has nine subsets and is good. ProofBy Lemma 1, we only consider the elements left of An. Case 1n ≡3(mod 9). Let n ≥3,i ≡1(mod 9), 1 ≤i ≤n −2. The only element of Anis just the element left of Suppose n ≥12, the elements left in the 3, 4, 5, 6, 7, 8, 9 and 10 -th columns of Ancan be partitioned into four good groups, then corresponding VDTC of C9is f(n,n−8,3,n−7,n,n−6,3,n−5,n,n−4,3,n−3,n,n−2,3,n,n−1,10),f(n,n−7,4,n−6,n,n−5,4,n−4,n,n−3,4,n−2,n,4,n−1,n,9,n−2),f(n,n−6,5,n−5,n,n−4,5,n−3,n,n−2,5,n,n−1,8,n,n−2,8,n−3)and f(n,n −5,6,n −4,n,n −3,6,n −2,n,6,n −1,n,7,n −2,n,n −3,7,n −4), respectively.when n=2, the conclusion is obtained. Suppose n ≥21 as follows. Let n ≥21,i ≡2(mod 9),11 ≤i ≤n−2. The elements left in the i,i+1,i+2,i+3,i+4,i+5,i+6,i+7 and i+8-th columns of Ancan be partitioned into five good groups,then corresponding VDTC of C9is f(n,n −9,i,n −8,n,n −7,i,n −6,n,n −5,i,n −4,n,n −3,i,n,i+8,n −1),f(n,n −8,i+1,n −7,n,n −6,i+1,n −5,n,n −4,i+1,n −3,n,n −2,i+1,n,n −1,i),f(n,n −7,i+2,n −6,n,n −5,i+2,n −4,n,n −3,i+2,n −2,n,i+2,n −1,n,i+7,n −2),f(n,n −6,i+3,n −5,n,n −4,i+3,n −3,n,n −2,i+3,n,n −1,i+6,n,n −2,i+6,n −3) and f(n,n −5,i+4,n −4,n,n −3,i+4,n −2,n,i+4,n −1,n,i+5,n −2,n,n −3,i+5,n −4),respectively. Case 2Let n ≥6,n ≡6(mod 9). The elements left in the 1, 2 and 3 -th columns of Ancan be partitioned into one good groups, then corresponding VDTC of C9is f(n,n −4,1,n −3,n,1,n −2,n −1,n,n −2,3,n,n −1,2,n,n −2,2,n −3). Let n ≥15,i ≡5(mod 9),5 ≤i ≤n−2. The elements left in the i,i+1,i+2,i+3,i+4,i+5,i+6,i+7 and i+8-th columns of Ancan be partitioned into five good groups,then corresponding VDTC of C9is f(n,n −9,i,n −8,n,n −7,i,n −6,n,n −5,i,n −4,n,n −3,i,n,i+8,n −1),f(n,n −8,i+1,n −7,n,n −6,i+1,n −5,n,n −4,i+1,n −3,n,n −2,i+1,n,n −1,i),f(n,n −7,i+2,n −6,n,n −5,i+2,n −4,n,n −3,i+2,n −2,n,i+2,n −1,n,i+7,n −2),f(n,n −6,i+3,n −5,n,n −4,i+3,n −3,n,n −2,i+3,n,n −1,i+6,n,n −2,i+6,n −3) and f(n,n −5,i+4,n −4,n,n −3,i+4,n −2,n,i+4,n −1,n,i+5,n −2,n,n −3,i+5,n −4).when n=15, the conclusion is obtained. Suppose n ≥24 as follows. Let n ≥24,i ≡6(mod 9),15 ≤i ≤n−2. The elements left in the i,i+1,i+2,i+3,i+4,i+5,i+6 and i+7-th columns of Ancan be partitioned into four good groups, then corresponding VDTC of C9is f(n,n −8,i,n −7,n,n −6,i,n −5,n,n −4,i,n −3,n,n −2,i,n,n −1,i+7),f(n,n −7,i+1,n −6,n,n −5,i+1,n −4,n,n −3,i+1,n −2,n,i+1,n −1,n,i+6,n −2),f(n,n −6,i+2,n −5,n,n −4,i+2,n −3,n,n −2,i+2,n,n −1,i+5,n,n −2,i+5,n −3) and f(n,n −5,i+3,n −4,n,n −3,i+3,n −2,n,i+3,n −1,n,i+4,n −2,n,n −3,i+4,n −4). Case 3Let n ≥9,n ≡0(mod 9). The elements left in the 1, 2, 3, 4, 5, 6 and 7 -th columns of Ancan be partitioned into three good groups, then corresponding VDTC of C9is f(n,n −7,1,n −6,n,n −5,1,n −4,n,n −3,1,n −2,n,7,n −1,n,6,n −2), f(n,n −6,2,n −5,n,n −4,2,n −3,n,n −2,2,n,n −1,5,n,n −2,5,n −3) and f(n,n −5,3,n −4,n,n −3,3,n −2,n,3,n −1,n,4,n −2,n,n −3,4,n −4). Let n ≥18,i ≡0(mod 9),0 ≤i ≤n−2. The elements left in the i,i+1,i+2,i+3,i+4,i+5,i+6 and i+7 -th columns of Ancan be partitioned into four good groups, then corresponding VDTC of C9is f(n,n −8,i,n −7,n,n −6,i,n −5,n,n −4,i,n −3,n,n −2,i,n,n −1,i+7),f(n,n −7,i+1,n −6,n,n −5,i+1,n −4,n,n −3,i+1,n −2,n,i+1,n −1,n,i+6,n −2),f(n,n −6,i+2,n −5,n,n −4,i+2,n −3,n,n −2,i+2,n,n −1,i+5,n,n −2,i+5,n −3) and f(n,n −5,i+3,n −4,n,n −3,i+3,n −2,n,i+3,n −1,n,i+4,n −2,n,n −3,i+4,n −4).when n=18, the conclusion is obtained. Suppose n ≥27 as follows. Let n ≥27,i ≡8(mod 9),17 ≤i ≤n−2. The elements left in the i,i+1,i+2,i+3,i+4,i+5,i+6,i+7 and i+8-th columns of Ancan be partitioned into five good groups,then corresponding VDTC of C9is f(n,n −9,i,n −8,n,n −7,i,n −6,n,n −5,i,n −4,n,n −3,i,n,i+8,n −1),f(n,n −8,i+1,n −7,n,n −6,i+1,n −5,n,n −4,i+1,n −3,n,n −2,i+1,n,n −1,i),f(n,n −7,i+2,n −6,n,n −5,i+2,n −4,n,n −3,i+2,n −2,n,i+2,n −1,n,i+7,n −2),f(n,n −6,i+3,n −5,n,n −4,i+3,n −3,n,n −2,i+3,n,n −1,i+6,n,n −2,i+6,n −3) and f(n,n −5,i+4,n −4,n,n −3,i+4,n −2,n,i+4,n −1,n,i+5,n −2,n,n −3,i+5,n −4). We can easily know that {n,1,n −1} do not belong to any good group. Lemma 3If n ≡4,8(mod 9),n ≥4, then all nonempty elements of Anexcept for{n,1,n −2}, {n,1,n −1} and {n,2,n −1} can be partitioned intogroups, such that each group has nine subsets and is good. ProofBy Lemma 1, we only consider the elements left of An. Case 1Let n ≥4,n ≡4(mod 9). Let i ≡1(mod 9), 1 ≤i ≤n −2, The three elements of Anis just the element left of An. Let n ≥13,i ≡3(mod 9), 3 ≤i ≤n −2. The elements left in the i, i+1, i+2, i+3, i+4,i+5, i+6, i+7 and i+8-th columns of Ancan be partitioned into five good groups, then corresponding VDTC of C9is f(n,n −5,i+1,n −4,n,n −3,i+1,n −2,n,i+1,n −1,i+5),f(n,n−4,i+2,n−3,n,n−2,i+2,n−1,n,n−2,i+4,n−1),f(n,n−5,i+7,n−4,n,n−3,i+7,n −2,n,i+7,n −1,i+11), f(n,n −4,i+8,n −3,n,n −2,i+8,n −1,n,n −2,i+10,n −1)and f(n,n −3,i+3,n −2,n,i+3,n −1,i+9,n,n −3,i+9,n −2), respectively. when n=13,the conclusion is obtained. Suppose n ≥22 as follows. Let n ≥22,i ≡4(mod 9),13 ≤i ≤n−2. The elements left in the i,i+1,i+2,i+3,i+4,i+5,i+6 and i+7 -th columns of Ancan be partitioned into four good groups, then corresponding VDTC of C9is f(n,n −8,i,n −7,n,n −6,i,n −5,n,n −4,i,n −3,n,n −2,i,n,n −1,i+7),f(n,n −7,i+1,n −6,n,n −5,i+1,n −4,n,n −3,i+1,n −2,n,i+1,n −1,n,i+6,n −2),f(n,n −6,i+2,n −5,n,n −4,i+2,n −3,n,n −2,i+2,n,n −1,i+5,n,n −2,i+5,n −3) and f(n,n −5,i+3,n −4,n,n −3,i+3,n −2,n,i+3,n −1,n,i+4,n −2,n,n −3,i+4,n −4),respectively. We can easily know that {n,1,n −2}, {n,1,n −1} and {n,2,n −1} do not belong to any good group. Case 2Let n ≥8,n ≡8(mod 9). The elements left in the 1, 2, 3, 4, 5 and 6-th columns of Ancan be partitioned into two good groups, then corresponding VDTC of C9is f(n,n −6,1,n −5,n,n −4,1,n −3,n,n −5,2,n −4,n,n −3,2,n,6,n −1)and f(n,n −4,3,n −3,n,n −2,3,n −1,n,n −3,4,n −2,n,4,n −1,n,5,n −2). Let n ≥17,i ≡7(mod 9), 7 ≤i ≤n −2. The elements left in the i, i+1, i+2, i+3, i+4,i+5, i+6, i+7 and i+8-th columns of Ancan be partitioned into five good groups, then corresponding VDTC of C9is f(n,n −5,i+1,n −4,n,n −3,i+1,n −2,n,i+1,n −1,i+5),f(n,n−4,i+2,n−3,n,n−2,i+2,n−1,n,n−2,i+4,n−1),f(n,n−5,i+7,n−4,n,n−3,i+7,n −2,n,i+7,n −1,i+11), f(n,n −4,i+8,n −3,n,n −2,i+8,n −1,n,n −2,i+10,n −1)and f(n,n −3,i+3,n −2,n,i+3,n −1,i+9,n,n −3,i+9,n −2), respectively. when n=17,the conclusion is obtained. Suppose n ≥26 as follows. Let n ≥26,i ≡8(mod 9),17 ≤i ≤n−2. The elements left in the i,i+1,i+2,i+3,i+4,i+5,i+6 and i+7 -th columns of Ancan be partitioned into four good groups, then corresponding VDTC of C9is f(n,n −8,i,n −7,n,n −6,i,n −5,n,n −4,i,n −3,n,n −2,i,n,n −1,i+7),f(n,n −7,i+1,n −6,n,n −5,i+1,n −4,n,n −3,i+1,n −2,n,i+1,n −1,n,i+6,n −2),f(n,n −6,i+2,n −5,n,n −4,i+2,n −3,n,n −2,i+2,n,n −1,i+5,n,n −2,i+5,n −3) and f(n,n −5,i+3,n −4,n,n −3,i+3,n −2,n,i+3,n −1,n,i+4,n −2,n,n −3,i+4,n −4),respectively. We can easily know that {n,1,n −2}, {n,1,n −1} and {n,2,n −1} do not belong to any good group. Lemma 4If n ≡5,7(mod 9),n ≥5, then all nonempty elements of Anexcept for{n,1,n −3}, {n,1,n −2}, {n,1,n −1}, {n,2,n −2}, {n,2,n −1} and {n,3,n −1} can be partitioned intogroups, such that each group has nine subsets and is good. ProofBy Lemma 1, we only consider the elements left of An. Case 1Let n ≥5,n ≡5(mod 9). Let i ≡1(mod 9), 1 ≤i ≤n −2. The six elements of Anis just the left element of An. Let n ≥14,i ≡5(mod 9),5 ≤i ≤n−2. The elements left in the i,i+1,i+2,i+3,i+4,i+5,i+6 and i+7 -th columns of Ancan be partitioned into four good groups, then corresponding VDTC of C9is f(n,n −8,i,n −7,n,n −6,i,n −5,n,n −4,i,n −3,n,n −2,i,n,n −1,i+7),f(n,n −7,i+1,n −6,n,n −5,i+1,n −4,n,n −3,i+1,n −2,n,i+1,n −1,n,i+6,n −2),f(n,n −6,i+2,n −5,n,n −4,i+2,n −3,n,n −2,i+2,n,n −1,i+5,n,n −2,i+5,n −3) and f(n,n −5,i+3,n −4,n,n −3,i+3,n −2,n,i+3,n −1,n,i+4,n −2,n,n −3,i+4,n −4),respectively. when n=14, the conclusion is obtained. Suppose n ≥23 as follows. Let n ≥23,i ≡4(mod 9), 13 ≤i ≤n −2. The elements left in the i, i+1, i+2, i+3, i+4,i+5, i+6, i+7 and i+8 -th columns of Ancan be partitioned into five good groups, then corresponding VDTC of C9is f(n,n −5,i+1,n −4,n,n −3,i+1,n −2,n,i+1,n −1,i+5),f(n,n−4,i+2,n−3,n,n−2,i+2,n−1,n,n−2,i+4,n−1),f(n,n−5,i+7,n−4,n,n−3,i+7,n −2,n,i+7,n −1,i+11), f(n,n −4,i+8,n −3,n,n −2,i+8,n −1,n,n −2,i+10,n −1)and f(n,n −3,i+3,n −2,n,i+3,n −1,i+9,n,n −3,i+9,n −2), respectively. We can easily know that {n,1,n −3}, {n,1,n −2}, {n,1,n −1}, {n,2,n −2}, {n,2,n −1}and {n,3,n −1} do not belong to any good group. Case 2Let n ≥7,n ≡7(mod 9). The elements left in the 1, 2, 3, 4 and 5-th columns of Ancan be partitioned into one good groups, then corresponding VDTC of C9is f(n,n −5,1,n −4,n,n −3,2,n −4,n,n −3,3,n −2,n,n −1,4,n,5,n −1). Let n ≥16,i ≡7(mod 9),7 ≤i ≤n−2. The elements left in the i,i+1,i+2,i+3,i+4,i+5,i+6 and i+7 -th columns of Ancan be partitioned into four good groups, then corresponding VDTC of C9is f(n,n −8,i,n −7,n,n −6,i,n −5,n,n −4,i,n −3,n,n −2,i,n,n −1,i+7),f(n,n −7,i+1,n −6,n,n −5,i+1,n −4,n,n −3,i+1,n −2,n,i+1,n −1,n,i+6,n −2),f(n,n −6,i+2,n −5,n,n −4,i+2,n −3,n,n −2,i+2,n,n −1,i+5,n,n −2,i+5,n −3) and f(n,n −5,i+3,n −4,n,n −3,i+3,n −2,n,i+3,n −1,n,i+4,n −2,n,n −3,i+4,n −4),respectively. when n=16, the conclusion is obtained. Suppose n ≥25 as follows. Let n ≥25,i ≡6(mod 9), 15 ≤i ≤n −2. The elements left in the i, i+1, i+2, i+3, i+4,i+5, i+6, i+7 and i+8-th columns of Ancan be partitioned into five good groups, then corresponding VDTC of C9is f(n,n −5,i+1,n −4,n,n −3,i+1,n −2,n,i+1,n −1,i+5),f(n,n−4,i+2,n−3,n,n−2,i+2,n−1,n,n−2,i+4,n−1),f(n,n−5,i+7,n−4,n,n−3,i+7,n −2,n,i+7,n −1,i+11), f(n,n −4,i+8,n −3,n,n −2,i+8,n −1,n,n −2,i+10,n −1)and f(n,n −3,i+3,n −2,n,i+3,n −1,i+9,n,n −3,i+9,n −2), respectively. We can easily know that {n,1,n −3}, {n,1,n −2}, {n,1,n −1}, {n,2,n −2}, {n,2,n −1}and {n,3,n −1} do not belong to any good group. Lemma 5If n ≡1,2(mod 9),n ≥10, then all elements of Anexcept forcan be partitioned intogroups, such that each group has exactly 9 subsets and is good. ProofBy Lemma 1, we only consider the elements left of An. Case 1Let n ≥10,n ≡1(mod 9). The elements left in the 1, 2, 3, 4, 5, 6, 7 and 8 -th columns of Ancan be partitioned into four good groups, then corresponding VDTC of C9is f(n,n−8,1,n−7,n,n−6,1,n−5,n,n−4,1,n−3,n,n−2,1,n,n−1,8),f(n,n−7,2,n−6,n,n−5,2,n−4,n,n−3,2,n−2,n,2,n−1,n,7,n−2),f(n,n−6,3,n−5,n,n−4,3,n−3,n,n−2,3,n,n−1,6,n,n−2,6,n−3)and f(n,n−5,4,n−4,n,n−3,4,n−2,n,4,n−1,n,5,n−2,n,n−3,5,n−4). Let n ≥18,i ≡0(mod 9), 0 ≤i ≤n −2. The elements left in the i, i+1, i+2, i+3, i+4,i+5, i+6, i+7 and i+8-th columns of Ancan be partitioned into five good groups, then corresponding VDTC of C9is f(n,n −5,i+1,n −4,n,n −3,i+1,n −2,n,i+1,n −1,i+5),f(n,n−4,i+2,n−3,n,n−2,i+2,n−1,n,n−2,i+4,n−1),f(n,n−5,i+7,n−4,n,n−3,i+7,n −2,n,i+7,n −1,i+11), f(n,n −4,i+8,n −3,n,n −2,i+8,n −1,n,n −2,i+10,n −1)and f(n,n −3,i+3,n −2,n,i+3,n −1,i+9,n,n −3,i+9,n −2), respectively. when n=18,the conclusion is obtained. Suppose n ≥28 as follows. Let n ≥28,i ≡1(mod 9),19 ≤i ≤n−2. The elements left in the i,i+1,i+2,i+3,i+4,i+5,i+6 and i+7 -th columns of Ancan be partitioned into four good groups, then corresponding VDTC of C9is f(n,n −8,i,n −7,n,n −6,i,n −5,n,n −4,i,n −3,n,n −2,i,n,n −1,i+7),f(n,n −7,i+1,n −6,n,n −5,i+1,n −4,n,n −3,i+1,n −2,n,i+1,n −1,n,i+6,n −2),f(n,n −6,i+2,n −5,n,n −4,i+2,n −3,n,n −2,i+2,n,n −1,i+5,n,n −2,i+5,n −3) and f(n,n −5,i+3,n −4,n,n −3,i+3,n −2,n,i+3,n −1,n,i+4,n −2,n,n −3,i+4,n −4),respectively. Case 2Let n ≥12,n ≡2(mod 9). The elements left in the 1, 2, 3, 4, 5, 6, 7, 8 and 9-th columns of Ancan be partitioned into five good groups, then corresponding VDTC of C9is f(n,n−9,1,n−8,n,n−7,1,n−6,n,n−5,1,n−4,n,n−3,1,n,9,n−1),f(n,n−8,2,n−7,n,n−6,2,n−5,n,n−4,2,n−3,n,n−2,2,n,n−1,1),f(n,n−7,3,n−6,n,n−5,3,n−4,n,n−3,3,n−2,n,i+2,n−1,n,8,n−2),f(n,n−6,4,n−5,n,n−4,4,n−3,n,n−2,4,n,n−1,7,n,n−2,7,n−3)and f(n,n −5,5,n −4,n,n −3,5,n −2,n,5,n −1,n,6,n −2,n,n −3,6,n −4), respectively. Let n ≥20,i ≡2(mod 9),2 ≤i ≤n−2. The elements left in the i,i+1,i+2,i+3,i+4,i+5,i+6 and i+7 -th columns of Ancan be partitioned into four good groups, then corresponding VDTC of C9is f(n,n −8,i,n −7,n,n −6,i,n −5,n,n −4,i,n −3,n,n −2,i,n,n −1,i+7),f(n,n −7,i+1,n −6,n,n −5,i+1,n −4,n,n −3,i+1,n −2,n,i+1,n −1,n,i+6,n −2),f(n,n −6,i+2,n −5,n,n −4,i+2,n −3,n,n −2,i+2,n,n −1,i+5,n,n −2,i+5,n −3) and f(n,n −5,i+3,n −4,n,n −3,i+3,n −2,n,i+3,n −1,n,i+4,n −2,n,n −3,i+4,n −4),respectively. when n=20, the conclusion is obtained. Suppose n ≥29 as follows. Let n ≥29,i ≡1(mod 9),19 ≤i ≤n−2. The elements left in the i,i+1,i+2,i+3,i+4,i+5,i+6,i+7 and i+8-th columns of Ancan be partitioned into five good groups,then corresponding VDTC of C9is f(n,n −9,i,n −8,n,n −7,i,n −6,n,n −5,i,n −4,n,n −3,i,n,i+8,n −1),f(n,n −8,i+1,n −7,n,n −6,i+1,n −5,n,n −4,i+1,n −3,n,n −2,i+1,n,n −1,i),f(n,n −7,i+2,n −6,n,n −5,i+2,n −4,n,n −3,i+2,n −2,n,i+2,n −1,n,i+7,n −2),f(n,n −6,i+3,n −5,n,n −4,i+3,n −3,n,n −2,i+3,n,n −1,i+6,n,n −2,i+6,n −3) and f(n,n −5,i+4,n −4,n,n −3,i+4,n −2,n,i+4,n −1,n,i+5,n −2,n,n −3,i+5,n −4),respectively. The proof is completed. How to obtain the optimal vertex-distinguishing total coloring of mC9(i.e. which use the minimum number of colors)? Firstly, let 2 ≤m ≤406, we determine the vertex-distinguishing total coloring of mC9. When m = 406, VDTC of mC9has used 29 colors and all 3-subsets of the set {1,2,··· ,29} of all colors used are the color sets of vertices in mC9, i.e, all 3-subsets of{1,2,··· ,29}has been used up. Secondly,we will give k−V DTC of mC9using colors 1,2,··· ,k whenrecursively. Finally,mC9are colored by the colors 1,2,··· ,k. Actually,k −V DTC ofcolored by the colors 1,2,··· ,k are only needed. Because of lettingthe restriction of k −V DTC ofin the former m C,9s is the k −V DTC of mC9. When the number of colors used in coloring varies from 3 to 29, the left 3-subsets in each cases are listed in Table-1. Table-1 Procedure of algorithm on the optimal VDTC ofmC9. For given m ≥2, find positive integer k such thatIf in some step the optimal vertex-distinguishing total coloring f ofhas been given, then the procedure should be stopped and optimal VDTC of mC9will be obtained by restricting f in first m C,9s. Step 1When m=2, χvt(mC9)≥6. The 6-VDTC of mC9will be given as follows. We use f(1,2,3,4,1,2,4,3,2,5,1,3,5,4,2,3,5,4)to color the first C9,all the color sets of 9 vertices in the first C9are given in the lines of n = 3,4,5 in Table 1 except {5,3,4}, the second C9can be obtained by Lemma 2, and all 3−element subsets of {1,2,··· ,6} except for {5,3,4},{6,1,5} are used up. When m=3, χvt(mC9)≥7, then based on the 6-VDTC of 2C9, we can obtain a k-VDTC of the three C9by Lemma 4, and all 3−element subsets of {1,2,··· ,7} except for {5,3,4},{6,1,5}, {7,1,4}, {7,1,5}, {7,1,6}, {7,2,5}, {7,2,6}, {7,3,6} are used up. When 4 ≤m ≤6, χvt(mC9) ≥8, then based on the 7-VDTC of 3C9, we can obtain a k-VDTC of the fourth, fifth C9by Lemma 3. These { {5,3,4}, {6,1,5}, {7,1,4}, {7,1,5},{7,1,6}, {7,2,5}, {7,2,6}, {7,3,6}, {8,1,6} } of unused 3−element subsets consist of a good group. We use the coloring f(1,6,5,3,4,7,1,5,7,1,6,7,2,5,7,3,6,8) to color the six-th C9, all the color sets of 9 vertices in the six-th C9are given in the lines of n = 5,6,7,8 in Table-1 except {8,1,7}, {8,2,7}, and all 3- element subsets of {1,2,··· ,8} except for {8,1,7}, {8,2,7}are used up. If a 3-subset of {1,2,··· ,k} is a color set of a vertex of mC9under a k-VDTC g of mC9,then this 3-subset is called used up under g. When 7 ≤m ≤9, χvt(mC9) ≥9, then based on the 8-VDTC of 6C9, we can obtain a k-VDTC of the seventh, eighth, ninth C9by Lemma 2, and all 3−element subsets of{1,2,··· ,9}except for {8,1,7}, {8,2,7}, {9,1,8} are used up. When 10 ≤m ≤13, χvt(mC9) ≥10, then based on the 9-VDTC of 9C9, we can obtain a k-VDTC of the tenth, eleventh, twelfth, thirteenth C9by Lemma 5, and all 3−element subsets of {1,2,··· ,10} except for {8,1,7}, {8,2,7}, {9,1,8} are used up. When 14 ≤m ≤18, χvt(mC9)≥11, then based on the 10-VDTC of 13C9, we can obtain a k-VDTC of the 14,15,··· ,18-th C9by Lemma 5, and all 3−element subsets of {1,2,··· ,11}except for {8,1,7}, {8,2,7}, {9,1,8} are used up. When 19 ≤m ≤24, χvt(mC9)≥12, then based on the 11-VDTC of 18C9, we can obtain a k-VDTC of the 19,20,··· ,24-th C9by Lemma 2, and all 3−element subsets of {1,2,··· ,12}except for {8,1,7}, {8,2,7}, {9,1,8}, {12,1,11} are used up. When 25 ≤m ≤31, χvt(mC9)≥13, then based on the 12-VDTC of 24C9, we can obtain a k-VDTC of the 25,26,··· ,31-th C9by Lemma 3, and all 3−element subsets of {1,2,··· ,13}except for{8,1,7},{8,2,7},{9,1,8},{12,1,11},{13,1,11},{13,1,12},{13,2,12}are used up. When 32 ≤m ≤40,χvt(mC9)≥14,then based on the 13-VDTC of 31C9,we can obtain a k-VDTC of the 32,33,··· ,40-th C9by Lemma 4. These{{8,1,7}, {8,2,7}, {9,1,8}, {12,1,11},{13,1,11}, {13,1,12}, {13,2,12}, {14,1,12}, {14,1,13} } of unused 3−element subsets consist of a good group. We use the coloring f(1,8,7,2,8,9,1,12,11,13,1,12,13,2,12,1,14,13) to color the 40-th C9, all the color sets of 9 vertices in the 40-th C9are given in the lines of n = 8,9,12,13,14 in Table-1 except {14,1,11}, {14,2,13}, {14,2,12}, {14,3,13}, and all 3-element subsets of {1,2,··· ,14} except for {14,1,11}, {14,2,13}, {14,2,12}, {14,3,13} are used up. When 41 ≤m ≤50, χvt(mC9)≥15, then based on the 14-VDTC of 40C9, we can obtain a k-VDTC of the 41,42,··· ,50-th C9by Lemma 2, and all 3−element subsets of {1,2,··· ,15}except for {14,1,11}, {14,2,13}, {14,2,12}, {14,3,13}, {15,1,14} are used up. When 51 ≤m ≤62, χvt(mC9) ≥16, then based on the 15-VDTC of 51C9, we can obtain a k-VDTC of the 51,52,··· ,62-th C9by Lemma 4. These { {14,1,11}, {14,2,12}, {14,3,13},{15,1,14},{16,1,13},{16,1,15},{16,2,14},{16,2,15},{14,2,13}}of unused 3−element subsets consist of a good group. We use the coloring f(1,11,14,13,2,12,14,3,13,16,1,14,15,16,2,14,16,15) to color the 62-th C9, all the color sets of 9 vertices in the 62-th C9are given in the lines of n = 14,15,16 in Table-1 except {16,1,14}, {16,3,15}, and all 3- element subsets of{1,2,··· ,16} except for {16,1,14}, {16,3,15} are used up. When 63 ≤m ≤75, χvt(mC9)≥17, then based on the 16-VDTC of 62C9, we can obtain a k-VDTC of the 63,64,··· ,75-th C9by Lemma 3, and all 3−element subsets of {1,2,··· ,17}except for {16,1,14}, {16,3,15}, {17,1,15}, {17,1,16}, {17,2,16} are used up. When 76 ≤m ≤90, χvt(mC9)≥18, then based on the 17-VDTC of 75C9, we can obtain a k-VDTC of the 76,77,··· ,90-th C9by Lemma 2, and all 3−element subsets of {1,2,··· ,18}except for {16,1,14}, {16,3,15}, {17,1,15}, {17,1,16}, {17,2,16}, {18,1,17} are used up. When 91 ≤m ≤107,χvt(mC9)≥19,then based on the 18-VDTC of 91C9,we can obtain a k-VDTC of the 91,92,··· ,107-th C9by Lemma 5, and all 3−element subsets of {1,2,··· ,19}except for {16,1,14}, {16,3,15}, {17,1,15}, {17,1,16}, {17,2,16}, {18,1,17} are used up. When 108 ≤m ≤126, χvt(mC9) ≥20, then based on the 19-VDTC of 107C9, we can obtain a k-VDTC of the 108,109,··· ,126-th C9by Lemma 5, and all 3−element subsets of{1,2,··· ,20} except for {16,1,14}, {16,3,15}, {17,1,15}, {17,1,16}, {17,2,16}, {18,1,17}are used up. When 127 ≤m ≤147, χvt(mC9) ≥21, then based on the 20-VDTC of 126C9, we can obtain a k-VDTC of the 127,128,··· ,147-th C9by Lemma 2, and all 3−element subsets of{1,2,··· ,21} except for {16,1,14}, {16,3,15}, {17,1,15}, {17,1,16}, {17,2,16}, {18,1,17},{21,1,20} are used up. When 148 ≤m ≤171, χvt(mC9) ≥22, then based on the 21-VDTC of 147C9, we can obtain a k-VDTC of the 148,149,··· ,171-th C9by Lemma 3. These { {16,1,14}, {16,3,15},{17,1,15}, {17,1,16}, {17,2,16}, {18,1,17}, {21,1,20}, {22,1,20}, {22,1,21} } of unused 3−element subsets consist of a good group. We use the coloring f(1,14,16,3,15,1,17,2,16,1,17,18,1,21,20,1,22,21) to color the 171-th C9, all the color sets of 9 vertices in the 171-th C9are given in the lines of n = 16,17,18,21,22 in Table-1 except {22,2,21}, and all 3- element subsets of {1,2,··· ,22} except for {22,2,21} are used up. When 172 ≤m ≤196, χvt(mC9) ≥23, then based on the 22-VDTC of 171C9, we can obtain a k-VDTC of the 172,173,··· ,196-th C9by Lemma 4, and all 3−element subsets of{1,2,··· ,23} except for {22,2,21}, {23,1,20}, {23,1,21}, {23,1,22}, {23,2,21}, {23,2,22},{23,3,22} are used up. When 197 ≤m ≤224, χvt(mC9) ≥24, then based on the 23-VDTC of 196C9, we can obtain a k-VDTC of the 197,198,··· ,224-th C9by Lemma 2, and all 3−element subsets of{1,2,··· ,24} except for {22,2,21}, {23,1,20}, {23,1,21}, {23,1,22}, {23,2,21}, {23,2,22},{23 ,3,22}, {24,1,23} are used up. When 225 ≤m ≤255, χvt(mC9) ≥25, then based on the 24-VDTC of 224C9, we can obtain a k-VDTC of the 225,226,··· ,255-th C9by Lemma 4. These { {22,2,21}, {23,1,20},{23,1,21}, {23,1,22}, {23,2,21}, {23,2,22}, {23,3,22}, {25,1,22}, {25,1,23} } of unused 3−element subsets consist of a good group. We use the coloring f(1,20,23,1,21,2,22,1,23,21,2,22,23,3,22,1,25,23)to color the 255-th C9,all the color sets of 9 vertices in 255-th C9are given in the lines of n = 22,23,25 in Table-1 except {25,1,24}, {25,2,23}, {25,2,24}, {25,3,24},{24,1,23},and all 3-element subsets of{1,2,··· ,25}except for{25,1,24},{25,2,23},{25,2,24},{25,3,24}, {24,1,23} are used up. When 256 ≤m ≤288, χvt(mC9) ≥26, then based on the 25-VDTC of 255C9, we can obtain a k-VDTC of the 256,257,··· ,288-th C9by Lemma 3, and all 3−element subsets of{1,2,··· ,26} except for {25,1,24}, {25,2,23}, {25,2,24}, {25,3,24}, {24,1,23}, {26,1,24},{26,1,25}, {26,2,25} are used up. When 289 ≤m ≤325, χvt(mC9) ≥27, then based on the 26-VDTC of 288C9, we can obtain a k-VDTC of the 289,290,··· ,325-th C9by Lemma 2. These { {25,1,24}, {25,2,23},{25,2,24}, {25,3,24}, {24,1,23}, {26,1,24}, {26,1,25}, {26,2,25}, {27,1,26} } of unused 3−element subsets consist of a good group. We use the coloring f(1,23,24,1,25,2,24,3,25,23,2,25,26,24,1,25,26,27) to color the 325-th C9, all the color sets of 9 vertices in the 325-th C9are given in the lines of n=24,25,26,27 in Table-1,and all 3-element subsets of{1,2,··· ,27}are used up. When 326 ≤m ≤364, χvt(mC9) ≥28, then based on the 27-VDTC of 325C9, we can obtain a k-VDTC of the 326,327,··· ,364-th C9by Lemma 5, and all 3−element subsets of{1,2,··· ,28} are used up. When 365 ≤m ≤406, χvt(mC9) ≥29, then based on the 28-VDTC of 364C9, we can obtain a k-VDTC of the 365,366,··· ,406-th C9by Lemma 5, and all 3−element subsets of{1,2,··· ,29} are used up. Now 406C9has been already colored using colors 1,2,··· ,29. When m ≥407, let 9m ≤k =30, goto Step 2. Step 2If k ≡3(mod 27), then based on thewe can obtain a k-VDTC ofby Lemma 2, and all 3−element subsets of {1,2,··· ,k} except for{k,1,k −1} are used up. Step 3If k ≡4(mod 27), then based on the (k −1)-VDTC ofwe can obtain a k-VDTC ofby Lemma 3,and all 3−element subsets of{1,2,··· ,k}except for {k −1,1,k −2}, {k,1,k −2}, {k,1,k −1}, {k,2,k −1} are used up. Step 4If k ≡5(mod 27), then based on the (k −1)-VDTC of, we can obtain a k-VDTC of−10]C9by Lemma 4. These {{k −2,1,k −3},{k −1,1,k −3},{k −1,1,k −2},{k −1,2,k −2},{k,1,k −3},{k,1,k −2},{k,1,k −1},{k,2,k −2},{k,2,k −1}} of unused 3−element subsets consist of a good group. We use the coloring f(1,k −3,k −2,k −1,1,k −3,k −1,k −2,2,k,1,k −2,k,k −1,2,k −2,k,k −1) to color the−1]C9-th, and all 3- element subsets of {1,2,··· ,k} except for {k,3,k −1} are used up. Step 5If k ≡6(mod 27), then based on the (k −1)-VDTC of, we can obtain a k-VDTC ofby Lemma 2,and all 3−element subsets of{1,2,··· ,k}except for {k −1,3,k −2}, {k,1,k −1} are used up. Step 6If k ≡7(mod 27), then based on the (k −1)-VDTC ofwe can obtain a k-VDTC ofby Lemma 4, and all 3−element subsets of {1,2,··· ,k}except for{k −2,3,k −3}, {k −1,1,k −2}, {k,1,k −3}, {k,1,k −2}, {k,1,k −1}, {k,2,k −2},{k,2,k −1}, {k,3,k −1} are used up. Step 7If k ≡8(mod 27), then based on the (k −1)-VDTC ofwe can obtain a k-VDTC ofby Lemma 3. These { {k −3,3,k −4}, {k −2,1,k −3},{k−1,1,k−4},{k−1,1,k−3},{k−1,1,k−2},{k−1,2,k−3},{k−1,2,k−2},{k−1,3,k−2},{k,1,k −2} } of unused 3−element subsets consist of a good group. We use the coloring f(1,k −2,k −3,3,k −4,k −1,1,k −3,k −1,1,k −2,k −1,2,k −3,k −1,3,k −2,k)to color theand all 3- element subsets of {1,2,··· ,k} except for {k,1,k −1}, {k,2,k −1}are used up. Step 8If k ≡9(mod 27), then based on the (k −1)-VDTCwe can obtain a k-VDTC ofby Lemma 2,and all 3−element subsets of{1,2,··· ,k}except for {k −1,1,k −2}, {k −1,2,k −2} are used up. Step 9If k ≡10(mod 27), then based on the (k −1)-VDTC ofwe can obtain a k-VDTC ofby Lemma 5,and all 3−element subsets of{1,2,··· ,k}except for {k −2,1,k −3}, {k −2,2,k −3}, {k −1,1,k −2} are used up. Step 10If k ≡11(mod 27), then based on the (k −1)-VDTC ofwe can obtain a k-VDTC ofby Lemma 5, and all 3−element subsets of {1,2,··· ,k}except for {k −3,1,k −4}, {k −3,2,k −4}, {k −2,1,k −3} are used up. Step 11If k ≡12(mod 27), then based on the (k −1)-VDTC ofcan obtain a k-VDTCC9by Lemma 2, and all 3−element subsets of {1,2,··· ,k}except for {k −4,1,k −5}, {k −4,2,k −5}, {k −3,1,k −4}, {k,1,k −1} are used up. Step 12If k ≡13(mod 27), then based on the (k −1)-VDTC of, we can obtain a k-VDTC ofby Lemma 3, and all 3−element subsets of {1,2,··· ,k}except for {k −5,1,k −6}, {k −5,2,k −6}, {k −4,1,k −5}, {k −1,1,k −2}, {k,1,k −2},{k,1,k −1}, {k,2,k −1} are used up. Step 13If k ≡14(mod 27), then based on the (k −1)-VDTC ofwe can obtain a k-VDTC ofby Lemma 4. These { {k −6,1,k −7}, {k −6,2,k −7},{k −5,1,k −6}, {k −2,1,k −3}, {k −1,1,k −3}, {k −1,1,k −2}, {k −1,2,k −2}, {k,1,k −2},{k,1,k −1} } of unused 3−element subsets consist of a good group. We use the coloring f(1,k −6,k −7,2,k −6,k −5,1,k −2,k −3,k −1,1,k −2,k −1,2,k −2,1,k,k −1)to color theand all 3- element subsets of {1,2,··· ,k} except for {k,1,k −3}, {k,2,k −2},{k,2,k −1}, {k,3,k −1} are used up. Step 14If k ≡15(mod 27), then based on the (k −1)-VDTC ofwe can obtain a k-VDTC of−5]C9by Lemma 2, and all 3−element subsets of {1,2,··· ,k}except for {k −1,1,k −4}, {k −1,2,k −3}, {k −1,2,k −2}, {k −1,3,k −2}, {k,1,k −1} are used up. Step 15If k ≡16(mod 27), then based on the (k −1)-VDTC ofwe can obtain a k-VDTC of11]C9by Lemma 4. These { {k −2,1,k −5}, {k −2,2,k −4},{k −2,2,k −3}, {k −2,3,k −3}, {k −1,1,k −2} {k,1,k −3}, {k,2,k −1}, {k,2,k −2},{k,2,k −1} } of unused 3−element subsets consist of a good group. We use the coloring f(1,k −5,k −2,k −3,2,k −4,k −2,3,k −3,k,1,k −2,k −1,k,2,k −2,k,k −1) to color the2]C9-th, and all 3- element subsets of {1,2,··· ,k} except for {k,1,k −2}, {k,3,k −1}are used up. Step 16If k ≡17(mod 27), then based on the (k −1)-VDTC ofwe can obtain a k-VDTC ofby Lemma 5, and all 3−element subsets of {1,2,··· ,k}except for {k −1,1,k −3}, {k −1,3,k −2}, {k,1,k −2}, {k,1,k −1}, {k,2,k −1} are used up. Step 17If k ≡18(mod 27), then based on the (k −1)-VDTC ofwe can obtain a k-VDTC ofby Lemma 2, and all 3−element subsets of {1,2,··· ,k}except for {k −2,1,k −4}, {k −2,3,k −3}, {k −1,1,k −3}, {k −1,1,k −2}, {k −1,2,k −2},{k,1,k −1} are used up. Step 18If k ≡19(mod 27), then based on the (k −1)-VDTC ofwe can obtain a k-VDTC ofby Lemma 5, and all 3−element subsets of {1,2,··· ,k}except for {k −3,1,k −5}, {k −3,3,k −4}, {k −2,1,k −4}, {k −2,1,k −3}, {k −2,2,k −3},{k −1,1,k −2} are used up. Step 19If k ≡20(mod 27), then based on the (k −1)-VDTC ofwe can obtain a k-VDTC ofby Lemma 5, and all 3−element subsets of {1,2,··· ,k }except for {k −4,1,k −6}, {k −4,3,k −5}, {k −3,1,k −5}, {k −3,1,k −4}, {k −3,2,k −4},{k −2,1,k −3} are used up. Step 20If k ≡21(mod 27), then based on the (k −1)-VDTC ofwe can obtain a k-VDTC ofby Lemma 2, and all 3−element subsets of {1,2,··· ,k}except for {k −5,1,k −7}, {k −5,3,k −6}, {k −4,1,k −6}, {k −4,1,k −5}, {k −4,2,k −5},{k −3,1,k −4}, {k,1,k −1} are used up. Step 21If k ≡22(mod 27), then based on the (k −1)-VDTC ofwe can obtain a k-VDTC ofby Lemma 3. These { {k −6,1,k −8}, {k −6,3,k −7},{k −5,1,k −7}, {k −5,1,k −6}, {k −5,2,k −6}, {k −4,1,k −5}, {k −1,1,k −2}, {k,1,k −2},{k,1,k −1} } of unused 3−element subsets consist of a good group. We use the coloring f(1,k −8,k −6,3,k −7,1,k −5,2,k −6,1,k −5,k −4,1,k −1,k −2,1,k,k −1) to color theand all 3- element subsets of {1,2,··· ,k} except for {k,2,k −1} are used up. Step 22If k ≡23(mod 27), then based on the (k −1)-VDTC ofwe can obtain a k-VDTC ofby Lemma 4, and all 3−element subsets of {1,2,··· ,k}except for {k −1,2,k −2}, {k,1,k −3}, {k,1,k −2}, {k,1,k −1}, {k,2,k −2}, {k,2,k −1},{k,3,k −1} are used up. Step 23If k ≡24(mod 27), then based on the (k −1)-VDTC ofwe can obtain a k-VDTC ofby Lemma 2, and all 3−element subsets of {1,2,··· ,k}except for {k −2,2,k −3}, {k −1,1,k −4}, {k −1,1,k −3}, {k −1,1,k −2}, {k −1,2,k −3},{k −1,2,k −2}, {k −1,3,k −2}, {k,1,k −1} are used up. Step 24If k ≡25(mod 27), then based on the (k −1)-VDTC ofwe can obtain a k-VDTC ofby Lemma 4. These { {k −3,2,k −4}, {k −2,1,k −5},{k −2,1,k −4}, {k −2,1,k −3}, {k −2,2,k −4}, {k −2,2,k −3}, {k −2,3,k −3}, {k,1,k −3},{k,1,k −2} } of unused 3−element subsets consist of a good group. We use the coloring f(1,k −5,k −2,1,k −4,2,k −3,1,k −2,k −4,2,k −3,k −2,3,k −3,1,k,k −2) to color theand all 3-element subsets of{1,2,··· ,k}except for{k−1,1,k−2},{k,1,k−1},{k,2,k −2}, {k,2,k −1}, {k,3,k −1} are used up. Step 25If k ≡26(mod 27), then based on the (k −1)-VDTC of, we can obtain a k-VDTC ofby Lemma 3, and all 3−element subsets of {1,2,··· ,k}except for {k −2,1,k −3}, {k −1,1,k −2}, {k −1,2,k −3}, {k −1,2,k −2}, {k −1,3,k −2},{k,1,k −2}, {k,1,k −1}, {k,2,k −1} are used up. Step 26If k ≡0(mod 27), then based on the (k −1)-VDTC ofwe can obtain a k-VDTC ofby Lemma 2. These { {k −3,1,k −4}, {k −2,1,k −3},{k−2,2,k−4},{k−2,2,k−3},{k−2,3,k−3},{k−1,1,k−3},{k−1,1,k−2},{k−1,2,k−2},{k,1,k −1} } of unused 3−element subsets consist of a good group. We use the coloring f(1,k −4,k −3,1,k −2,2,k −3,3,k −2,k −4,2,k −2,k −1,k −3,1,k −2,k −1,k) to color the-th, and all 3- element subsets of {1,2,··· ,k} are used up. Step 27If k ≡1(mod 27), then based on the (k −1)-VDTC ofwe can obtain a k-VDTC ofby Lemma 5, and all 3−element subsets of {1,2,··· ,k} are used up.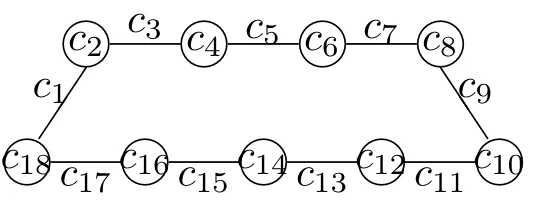
§3. The Thought of Algorithm

§4. Procedure of Algorithm
 Chinese Quarterly Journal of Mathematics2019年3期
Chinese Quarterly Journal of Mathematics2019年3期
- Chinese Quarterly Journal of Mathematics的其它文章
- Normality Criteria of Zero-free Meromorphic Functions
- On Uniqueness Problem of Meromorphic Functions Sharing Values with Their q-shifts
- Finite Difference Methods for the Time Fractional Advection-diffusion Equation
- Globally Bounded Solutions in A Chemotaxis Model of Quasilinear Parabolic Type
- Triple Positive Solutions for a Third-order Three-point Boundary Value Problem
- Fixed-time Consensus for Leader-follower Second-order Multi-agent Systems
