基于第一性原理的晶体材料力学性能计算方法

孙金芳,姚星星,倪程鹏,耿 杰

(安徽信息工程学院 通识教育与外国语学院,安徽 芜湖 241000)

0 引 言

晶体材料的主要性能为力学性能,目前获取晶体材料性能最好的方法是试错,该方法可以从周期表内找出多种化学元素组合,分析材料蕴含成分公式,效果比较显著,但花费时间很长,成本很高[1]。所以寻找有效的力学性能计算方法十分重要。伴随着计算机与建模方法的高速发展,不同材料的建模方法与电子结构的原理研究得到了很大进步,通过求解化学与晶体的自洽方程和产生的电子波函数,可以计算出晶体材料力学性能,计算过程大多数需要依赖电子,因此需要用原子核与固体来约束,从而实现电子结构预测[2]。

目前,相关学者已经对晶体材料力学性能计算方法进行了研究并取得了一些成果。文献[3]提出了一种基于密度泛函理论的第一性原理平面波赝势法,在理想状态下,运用密度泛函理论分析空位因素对B2-NiAl力学性能的影响作用,实验结果表明该方法能够计算出晶体材料的力学性能,但是计算结果与实际值偏差较大；文献[4]运用第一性原理对B2型TiSi合金的缺陷结构进行了计算,包括弹性性质和晶格常数,根据计算结果可知,B2型TiSi合金结构的韧性不高,虽然得出了比较可靠的结论,但是该方法计算时间较长,实用性不高。根据上述分析可知,虽然目前对于如何更好地计算出晶体材料的力学性能已经有了一些研究成果,但是已有方法仍然存在一些缺陷。运用传统计算方法对晶体材料的力学性能进行计算时得到的结果并不理想,主要是因为计算时电子、原子、介质等各种因素的影响,除此之外,传统方法具有晶体结构敏感、晶体缺陷(晶体的空缺、间隙、错位、错层、结界)等问题。

为解决传统方法存在的问题,给出了基于第一性原理的晶体材料力学性能计算方法。第一性原理根据原子核和电子相互作用原理,从量子力学角度出发,利用近似处理求解,该原理通过硬性规定分析,具有很好的移植性。实验结果表明,该方法具有有效性。

1 计算方法

计算晶体材料力学性能要从强度、延性、韧性、弹性、刚性和晶格缺陷等多个角度考虑。本文从强度、弹性和晶格缺陷3个角度进行探讨。

1.1 晶体材料强度

晶体强度通过连接方法计算, 连接方法是一种无害的环境技术[5]。 运用增量应力将非应变晶体进行拉伸或者剪切, 通过第一性原理, 获取最终应力。 晶体强度性能的理想强度可以称为最大应力, 计算理想强度能够解决材料不稳定的问题[6]。 利用第一性原理计算理想强度的材料很多, 其中, 对于弹性不稳定的晶体材料来说, 其扩展方式有很多种, 因此强度性能计算也更加复杂,需要大量的计算资源[7]。由于受到外力时,晶体材料的内力与外力相同,因此可以通过计算在单位面积上所受的外力计算内力，即

σ=F/A

(1)

式中:σ为晶体材料产生的内力,N/m2;F为受到的外力;A为晶体材料的面积。晶体材料中的应力分量见图1。

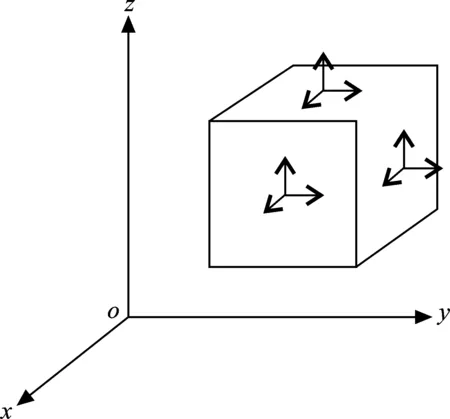
图1 晶体材料中的应力分量Fig.1 Stress components in crystal materials

如图1所示，在分析晶体材料中的应力分量时,要在一个点上建立三维坐标轴,根据建立的三维坐标轴得出正六面体,对每个截面都要进行应力分解,得到的应力为切应力,一个质心上对应三个正应力和六个切应力[8]。被计算的晶体材料强度性能多指理想强度性能,而理想强度只在完美的晶体中存在,在实际生活中,每个晶体都有着晶格缺陷,因此要从存在的晶格缺陷中分析固有材料特性,从而更加准确地计算晶体材料强度[9]。

1.2 晶体材料弹性

对于晶体材料来说,弹性性能也是计算晶体材料力学性能时应该重点考虑的内容之一。当材料受到外力之后,会出现形状和尺寸的变化,这种现象称为形变,此时原子和离子之间的相对位置和相对距离会改变,为了避免这种情况,分子中的原子和离子会自动产生附加内力,阻挡外力导致的形状变化[10]。当内力和外力达到平衡以后,内力和外力的大小是相等的,但是方向不同。晶体材料在单位面积上受到的内力为应力,产生的变化为应变,可通过Δl/l计算，其中l为变形前长度，Δl为变形后的伸长量。

对于不同晶体材料来说,在相同的应力下,产生的应变程度不同。一些无机晶体材料,在发生弹性形变之后,材料自身产生的应力非常小,相对应的塑性形变也非常小,甚至无法产生形变,在这种情况下,该晶体材料就会发生断裂,此晶体材料被称为脆性材料;对于一些有机晶体材料来说,在发生弹性形变之后,材料自身产生的应力很大,相对应的塑性形变也很大,材料会从弹性形变转变成塑性形变,最后才会发生断裂[11],形变能力极强。还有一些晶体材料,应变能力超过普通的晶体材料,在受到外力之后,不会出现弹性形变,这类材料被称之为弹性晶体材料[12]。不同材料在拉伸条件下,应变与应力的变化曲线如图2所示。

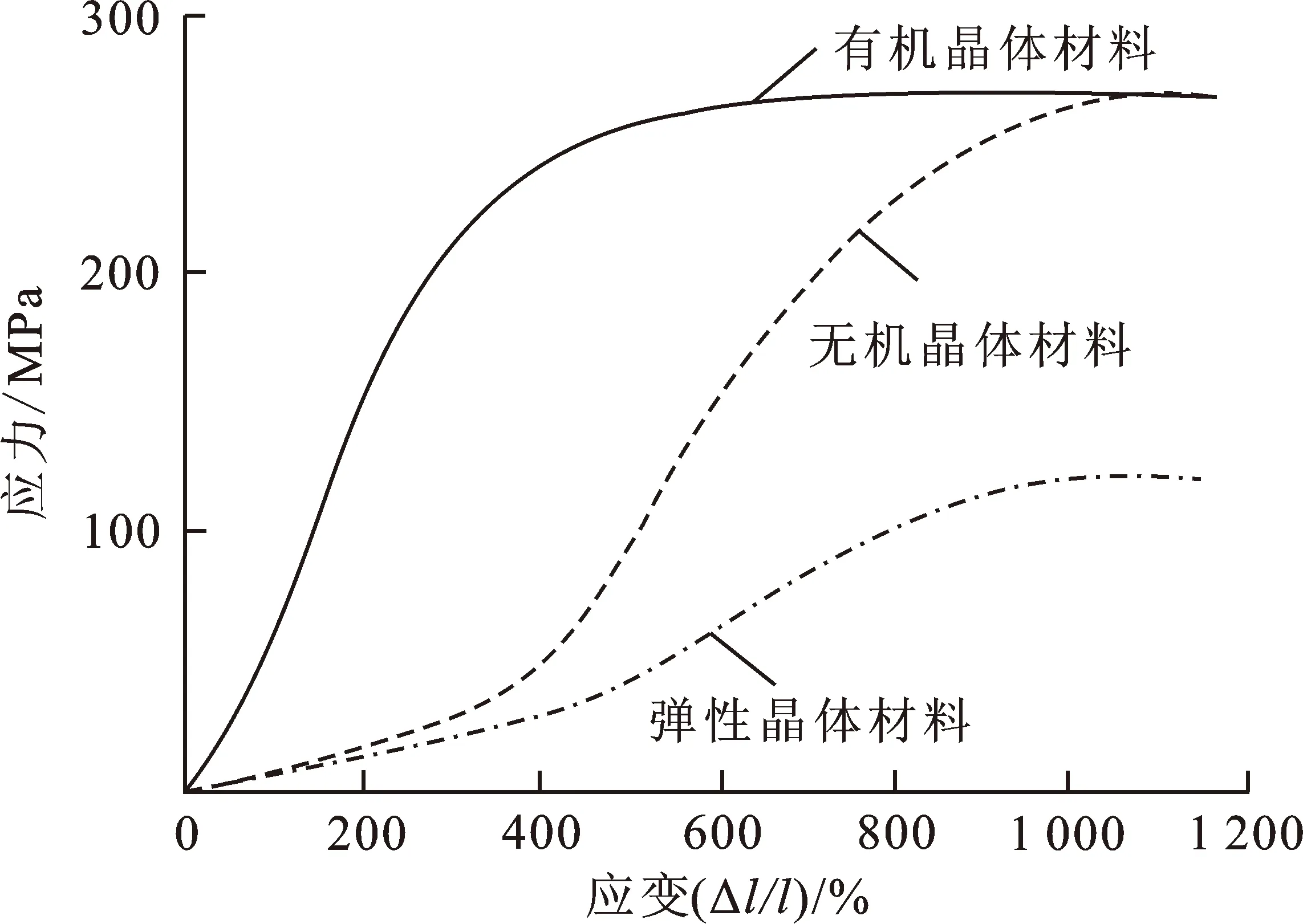
图2 应变与应力的变化曲线Fig.2 Variation curves of strain and stress

利用弹性性能能够较为直观地推理出晶体材料力学性能,晶体的强度性能与材料形变呈现非线性响应关系,而弹性性能与材料形变呈现线性响应关系[13]。通过第一性原理能够推理出晶体在平衡位置产生的一系列形变,最终判断出应变力的结果。弹性形变与总能量之间会出现耦合关系,为了推导出这一关系结果,需得到晶体的弹性常数[14]。

目前很多晶体材料都具有强度高、熔化温度高等特点,可以广泛应用在高温领域,计算它们的弹性常数时,必须使用第一性原理[15]。当晶体材料中的原子占据晶格位置时,材料结构会变得更加复杂,内部含有的原子分布方式更加随机。如果按照传统的方法计算,那么在每一个晶格中只能计算出一种原子,得到的结果准确度相对较低。第一原理能够利用近似值计算出晶格中的所有原子,反复校准,直到得到相对精准的结果。利用第一原理计算弹性常数时,得到的弹性模量也是不同的,除了得到弹性模量之外,还会得到体积模量、剪切模量和杨氏模量,根据这些数据可以建立出平均系统,分析晶体材料的延展性和可塑性[16]。晶体材料内部分子之间的作用力效果如图3所示。

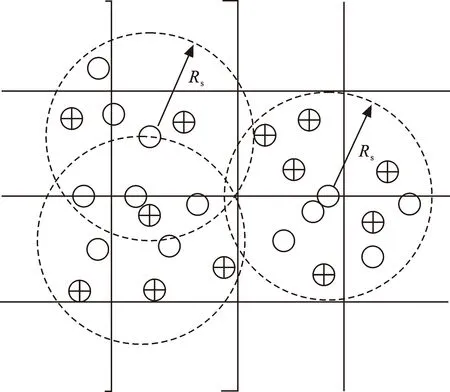
图3 晶体材料内部分子作用力效果Fig.3 Effect of molecular force on crystalmaterials

研究金属与无机材料之间的关系对于理解晶体材料的弹性性能具有重要意义,晶体材料独有的键合类型可以将分子以链的方式连接起来,使晶体材料的弹性结构更加稳定[17]。

分析晶体材料的弹性性能时需要对泊松比进行计算。晶体材料的泊松比在0.3～1.0之间波动,当晶体化合物低于0.2时,该材料不具备脆性。体积模量与剪切模量之间的比值反映了晶体材料的韧性,当体积模量与剪切模量之间的比值很大时,晶体材料的韧性也很大;当体积模量与剪切模量之间的比值很小时,晶体材料的韧性很小。通过这一结果可以分析晶体材料内部结构,判断局部是否出现腐蚀以及中间硬度[18]。利用第一原理除了能够得到晶体材料的弹性常数,还能得到晶体材料的二元弹性常数,如果二元弹性常数趋近于0,则认为晶体材料具有超塑性,如果二元弹性常数趋近于1,则认为晶体材料具有超弹性,根据理论体系分析出晶体材料内部指标,以此预测晶体材料的力学性能。

1.3 晶体材料晶格缺陷

每一个晶体材料都会存在晶格缺陷, 晶格缺陷直接影响其力学性能。 使用传统方法计算晶体材料时, 考虑的都是理想材料, 得到的结果准确性很低。 晶格缺陷会导致晶体材料力学性能与理想状态力学性能有很大差别, 甚至不足理想状态的1/1 000。 为了得到更加准确的计算结果, 分析它们的晶格缺陷十分重要。 本文根据晶体的空间布局, 引入第一性原理, 从零维缺陷、一维缺陷和二维缺陷的角度分析晶体材料的力学缺陷, 进而分析晶体材料的力学性能[19]。

晶体材料的零维缺陷是由晶体材料的原子扩散特性决定的,合金原子在受到外力时,会出现相互作用,并且对空缺的晶格产生吸引力,引发晶体的抗蠕变特性,一旦触发这种特性,很难再次发生改变。合金原子和晶格之间的作用力会导致材料内部出现错位,向不同的位置滑动,引发一维缺陷[20]。由于错位的存在,在计算材料的连续弹性时,也会出现很大的局限性。晶体材料出现错位会导致不同位置的晶胞之间出现相互作用,如果只计算单体,也很难得到错位结果。错位会打破几何的周期对称结构,因此必须建立错位急诊模型,研究可能出现的错位结构,多次对比,找出吻合度最高的结构。

相比一维缺陷,二维缺陷更加复杂,二维缺陷出现的层错和孪晶会更加严重影响晶体结构,破坏晶体的可塑性,利用第一原理分析二维缺陷时,要对固有层产生的错能和不稳定层产生的错能进行比较,从而得到比较准确地分析结果。零维缺陷、一维缺陷和二维缺陷位于不同层面,它们之间也会产生相互作用,导致分析结果更加复杂。建立一个统一的三维坐标轴,在不同层面中得到应力分量,并按照正、负将受到的应力分开,当受到的应力与建立的坐标轴方向一致时,应力为正;当受到的应力与建立的坐标轴方向相反时,应力为负。构建晶体材料力学性能的计算模型如式(2)所示。

(2)

根据x,y,z寻找对应的应力分量值,从而计算出晶体材料的力学性能。

2 实验研究

为了检测基于第一性原理的晶体材料力学性能计算方法实际工作效果,与传统计算方法进行对比,设计了对比实验。

2.1 实验参数

实验工作参数如下:设定计算周期为15 h,计算的最大容量为1 500 bit,计算时使用的电源频率为20 Hz,电源电流为500 A,电源电压为50 V,内部3个电阻分别为15 Ω,40 Ω,90 Ω,工作时环境温度为15 ℃～50 ℃,在互联网环境下进行工作,运行的工作平台为云平台,运行系统为Windows 10。实验选取离子晶体作为研究对象,该类晶体材料各项参数如表1所示。

表1 晶体材料参数Table 1 Crystaline materials parameters

晶体一般可以划分成7种不同的晶系,设置不同类型晶格参数,如表2所示,其中a,b,c表示棱边长度；α,β,γ表示夹角。

表2 晶体材料的不同晶格类型Table 2 Different lattice types of crystaline materials

2.2 结果与分析

根据上述设定的参数进行实验,利用传统计算方法和本文计算方法分别计算多晶材料、单晶材料以及纳米晶材料力学性能,比较2种计算方法的准确性,根据实验结果分析2种方法的工作效果。得到的实验结果分别如图4，5，6所示。其中准确率的计算公式为

(3)

式中：a1为实验测试得到的力学性能结果；a2为晶体材料的实际力学性能。

图4 2种多晶材料力学性能计算结果图Fig.4 Two kinds of calculation results of mechanical property of crystalline materials

从图4可知,在计算多晶材料力学性能时,当计算时间为1 min,传统方法结果准确率为65%,本文方法结果准确率为78%;当计算时间为3 min,传统方法结果准确率为60%,本文方法结果准确率为70%;当计算时间为5 min,传统方法结果准确率为58%,本文方法结果准确率为87%。说明对多晶材料力学性能进行计算时,本文方法结果的准确性在整体上优于传统方法。

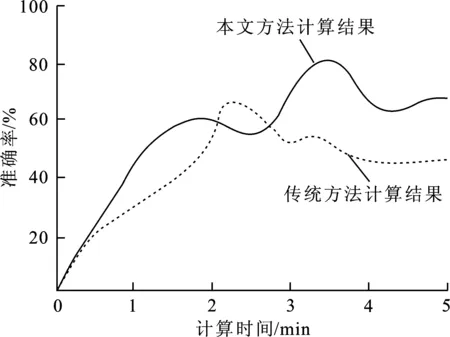
图5 2种单晶材料力学性能计算结果图Fig.5 Two kinds of calculation results of mechanical property of single crystaline materials

从图5可知,单晶材料力学性能与多晶材料力学性能较为相似。在计算单晶材料力学性能时,当计算时间为1 min,传统方法结果准确率为29%,本文方法结果准确率为45%;当计算时间为3 min,传统方法结果准确率为52%,本文方法结果准确率为70%;当计算时间为5 min,传统方法结果准确率为48%,本文方法计算结果准确率为68%。针对单晶材料进行力学性能计算时,虽然传统方法和本文方法的计算准确率都存在不稳定性,但是本文方法结果的可靠性仍然优于传统方法。

图6 2种纳米晶材料力学性能计算结果图Fig.6 Two kinds of calculation results of mechanical property of nanocrystalline materials

纳米晶材料力学性能十分复杂,从图6可知,传统方法与本文方法的计算结果准确率都不高。在计算纳米晶材料力学性能时,当计算时间为1 min,传统方法计算结果准确率为42%,本文方法计算结果准确率为37%;当计算时间为3 min,传统方法计算结果准确率为37%,本文方法计算结果准确率为39%;当计算时间为5 min,传统方法计算结果准确率为36%,本文方法计算结果准确率为50%。通过上述数据分析可知,在对纳米晶材料的力学性能进行计算时,本文方法和传统方法的计算准确性处于较低的水平,说明运用本文提出的计算方法并不能有效应用于对纳米晶材料力学性能的计算中。因此,研究针对纳米晶材料的计算方法是未来研究工作中的重点内容。

3 结 语

研究晶体力学材料性能对于物质的研发有着很大的意义,但是传统的方法多是从理想状态进行研究,得到的结果与实际值有着很大的不同,不能够为研究带来有效的参考意义。第一性原理对于结构材料的研究有着实用价值,本文基于第一性原理研究了一种新的晶体材料力学性能计算方法,通过同时分析晶体材料的弹性性能、强度性能和晶格缺陷,完成力学性能的分析,降低了研究材料时的复杂性。实验结果表明,运用所提方法对晶体材料的力学性能进行计算，所得到的结果精确度较高,对设计新的复合型材料有着极为重要的指导意义。未来将致力于纳米晶材料力学性能的计算工作,为了得到更加准确的计算结果,还要进一步研究。