网络搜索数据和GWO-SVR模型的旅游短期客流量预测

王兰梅， 陈崇成， 叶晓燕， 潘淼鑫， 2

(1. 福州大学空间数据挖掘与信息共享教育部重点实验室， 地理空间信息技术国家地方联合工程研究中心， 福建 福州 350108； 2. 福建师范大学数学与信息学院， 福建省公共服务大数据挖掘与应用工程技术研究中心， 福建 福州 350117)

0 引言

随着旅游业的快速发展， 人们生活品质的提高， 休闲旅游成为一种时尚. 各著名景区常发生的游客扎推和拥挤等安全事件， 给景区管理和游客旅游均带来困扰. 为避免该类事件的发生， 景区管理者应掌握短期内游客流量的预测数据， 以便制定合理的分流方案. 20世纪， 国际上主要用经典时间序列模型和计量经济学模型[1]开展旅游需求研究， 但存在非线性拟合能力差的缺点. 随着人工智能算法的发展， 学者们开始将BP神经网络(back propagation neural network， BPNN)[2]和支持向量回归(support vector regression， SVR)[3]等算法应用于旅游客流量预测领域[4]. SVR在解决小样本、 非线性时间序列预测中表现出许多特有的优势， 但是其参数选择是影响预测精度的重要因素. 人们优化SVR参数的智能化算法主要包括布谷鸟搜索(cuckoo search， CS)和粒子群算法(particle swarm optimization， PSO)[5]等. Chen等[6]提出以SVR和GA结合的GA-SVR模型预测中国入境游客流量， 结果显示GA-SVR模型明显优于BPNN和ARIMA模型. 灰狼算法(grey wolf optimization， GWO)是由Mirjalili等[7]提出的一种群体智能算法， 其在全局寻优方面明显优于GA、 CS和PSO等智能化优化算法[8-9]. 互联网时代背景下， 学者也尝试将网络搜索数据应用在旅游客流量预测中， 取得不错的效果[10-12]. Sun等[13]将旅游历史客流量数据与百度指数、 谷歌指数相结合用到客流量预测中， 发现预测效果有显著提高. 本研究将网络搜索数据加入旅游客流量预测中， 利用GWO算法优化SVR的参数， 并用参数优化后的SVR模型实现旅游客流量的预测.

1 方法研究

1.1 支持向量回归基本原理

SVR主要是通过一个非线性映射函数， 把训练样本变换到高维特征空间(可能是无限维)， 使得在高维空间中样本的分布更有规律性, 以便构造线性决策函数[14]. 对于给定的数据集合T=(xi,yi)，i=1, 2, …,n，xi∈Rn，yi∈R， 这里xi为输入值， 即客流量的影响因素，yi为xi相对应的输出值， 即客流量的预测值，n为训练样本的数目， 目标是找出样本在高维特征空间的回归函数[15].

f(x)=w×φ(x)+b

(1)

其中：f(x)为待拟合预测函数；φ(x)为非线性映射函数；w和b分别为权重和偏置， 通过惩罚风险函数R(C)获得.

(2)

引入非负松弛变量δ和δ*， 则式(2)等价于：

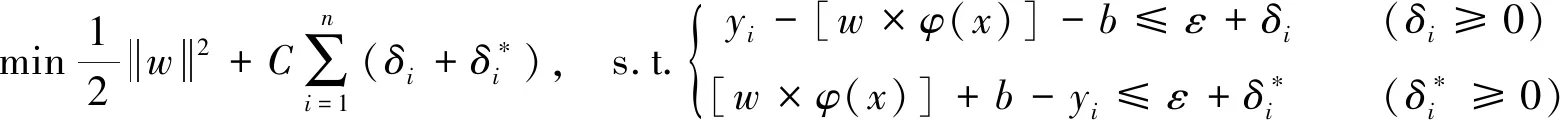
(3)

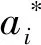
(4)

利用KKT(Karush-Kuhn-Tucker)条件， 最终得到SVR函数.

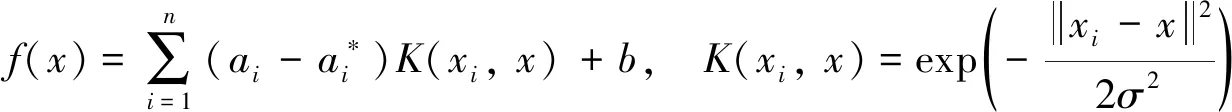
(5)

其中:xi为训练集输入值，x为测试集输入值.

1.2 灰狼算法基本原理

GWO算法主要包含灰狼群体社会等级的划分、 包围、 猎捕和攻击等方面内容[7].

1) 灰狼社会等级的划分. GWO算法中， 将灰狼按照适应度值分为四个等级.

2) 包围. 进行狩猎时， 灰狼需要对猎物进行包围， 狼群个体间的位置不断发生更新. 包围行为的公式为

D=|C×Xp(t)-X(t)|,X(t+1)=Xp(t)-A×D

(6)

其中：D为灰狼个体与猎物之间的距离；Xp为食物的位置(即全局最优解位置)；X为灰狼的位置(即潜在解位置)；t为当前迭代次数，A和C为系数向量.

3) 猎捕. 灰狼包围猎物后， 开始猎捕， 一般由α、β和δ引导，ω则根据α、β和δ的位置更新各自的位置.

Dα=|C1×Xα-X|,Dβ=|C2×Xβ-X|,Dδ=|C3×Xδ-X|

(7)

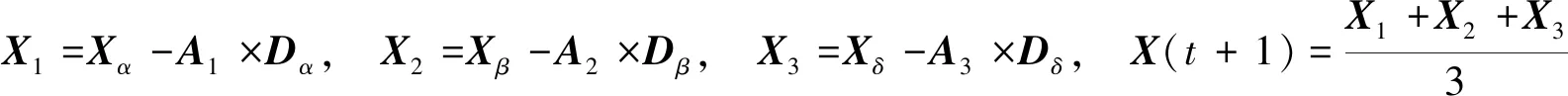
(8)

其中：Dα、Dβ、Dδ分别表示为灰狼α、β和δ与灰狼ω之间的距离；X(t+1)为更新后灰狼的位置.

4) 攻击. 在攻击阶段， 灰狼完成抓获猎物的使命， GWO算法取得最优解.

1.3 基于灰狼算法的支持向量回归参数优化

利用经过GWO算法参数优化后的SVR模型对景区客流量进行建模预测， 具体步骤如下：

1) 对景区客流量等相关数据进行预处理， 确定输入和输出变量.

2) 设置SVR参数(c，g)的取值范围， 并设置相关参数.

3) 在规定范围内初始化各灰狼个体的位置Xi为(1, 2, …,N)， 并对参数a，A和C进行初始化.

4) 计算种群中各灰狼个体的适应度值， 并排序选取最优的3只灰狼个体， 依次取名为α、β、δ.

5) 计算其他灰狼ω与3只最优灰狼的距离， 更新各灰狼ω的位置， 同时更新参数a，A和C的值.

6) 判断是否达到最大迭代次数， 输出适应度最佳的灰狼Xα， 利用最优的参数(c，g)建立SVR预测模型.

2 实证分析

2.1 数据来源

以四川省九寨沟和四姑娘山两个景区为例， 实验数据如表1所示. 选择百度指数作为网络搜索数据的代表. 因GWO-SVR模型建立的过程是一样的， 九寨沟景区详细介绍， 四姑娘山景区在2.5节中简要说明.

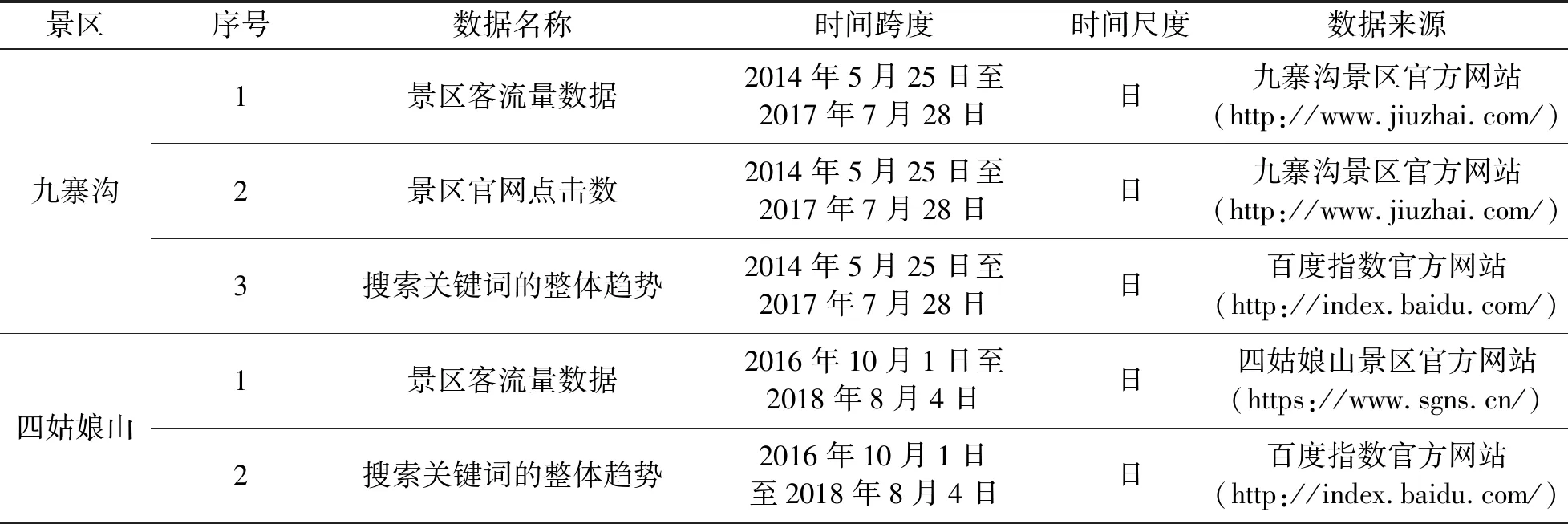
表1 九寨沟和四姑娘山实验数据说明

2.2 搜索关键词的选择

选择和收集代表游客兴趣和搜索行为的候选关键词， 主要有以下五个步骤组成：

1) 确定初始搜索关键词. 选取“九寨沟”“九寨沟旅游”“九寨沟攻略”“九寨沟天气”为初始搜索关键词.

2) 扩展搜索关键词. 利用初始搜索关键词， 借助百度指数网站的需求图谱功能、 相关词工具官网(http://www.78901.net/keywords/)的查询相关词功能和爱站网(https://ci.aizhan.com/)的关键词挖掘模块等工具， 进一步扩展与特定景区旅游相关的搜索关键词. 经过简单筛选， 共选择48个关键词， 如表2所示.

表2 九寨沟旅游搜索关键词

续表2

3) 获取搜索关键词的整体趋势. 用Java爬虫程序批量获取48个搜索关键词的每日的整体趋势数据.

4) 计算关键词整体趋势与客流量的相关性. 用皮尔森相关系数R作筛选搜索关键词， 计算每个搜索关键词与客流量1～14 d提前期的R值. 同一搜索关键词中， 选择R值最大的提前期作为该关键词的最佳提前期.

为验证相关系数法筛选关键词提前期的有效性， 以四姑娘山客流量为例， 设计小实验如下.

输入变量为昨日客流量和关键词“四姑娘山天气”的搜索数据， 输出变量为旅游客流量数据. 训练数据集为2016年10月30日到2018年7月15日的前624 d数据， 测试数据集为2018年7月16日到2018年8月4日共20 d的数据. 对关键词“四姑娘山天气”的提前期1～14 d分别建立GWO-SVR客流量预测模型， 用平均绝对百分误差(mean absolute percentage error， MAPE)作为预测精度指标. 计算关键词“四姑娘山天气”1～14 d提前期与客流量之间的R值以及每个模型的平均绝对百分误差. 相关系数与预测精度的对比如表3所示.

表3 R值与预测精度的对比

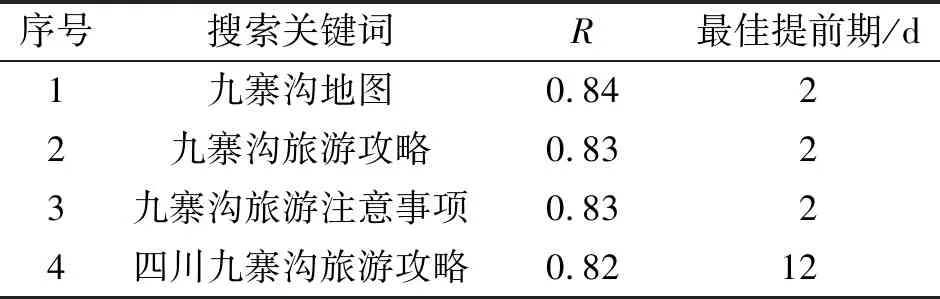
表4 R > 0.8的九寨沟搜索关键词

从表3中可见，R值最大时的提前期为2 d， 与预测精度最高的提前期相同， 且预测精度远高于其他提前期精度.R值第二大时的提前期为3 d， 此时的预测精度为第二高.R值第三大时的提前期为1 d， 此时的预测精度为第三高. 因此， 用相关系数法筛选关键词提前期是有效的.

5) 确定最终关键词. 设置关键词的R阈值， 确定最终关键词.R阈值设为0.8， 搜索关键词如表4所示.

2.3 GWO-SVR模型的建立

以2014年5月25日至2017年7月8日共1 141 d的数据为训练集， 以2017年7月9日至2017年7月28日共20 d的数据为测试数据集. 输入变量为昨日客流量、 前日客流量、 去年同日客流量、 前年同日客流量、 昨日官网点击数、 时间特征信息(主要是星期特征)、 最佳提前期搜索关键词的整体趋势; 输出变量为旅游客流量数据. 设置灰狼优化算法的最大迭代次数100， 种群规模50. 参数c取值范围为[0.01， 100]， 参数g取值范围为[0.01， 100]. 将灰狼优化算法得到的最优参数(c，g)带入到SVR中， 建立SVR模型对客流量进行预测.

2.4 结果分析

在建立GWO-SVR模型后， 构建ARIMA、 BPNN、 SVR、 PSO-SVR、 CS-SVR和无网络搜索数据(没有网络搜索数据的GWO-SVR模型)等6个对比模型. 九寨沟客流量原值与7个预测模型的预测值的对比结果如图1所示. 选择平均绝对误差(mean absolute error， MAE)、 均方误差(mean squared error， MSE)和平均绝对百分误差3个指标来衡量模型的预测性能. 6个预测模型在九寨沟旅游客流量预测中的性能比较结果如表5所示.

图1 九寨沟客流量的原值与预测值Fig.1 Original and predicted tourist flow in Jiuzhaigou Valley

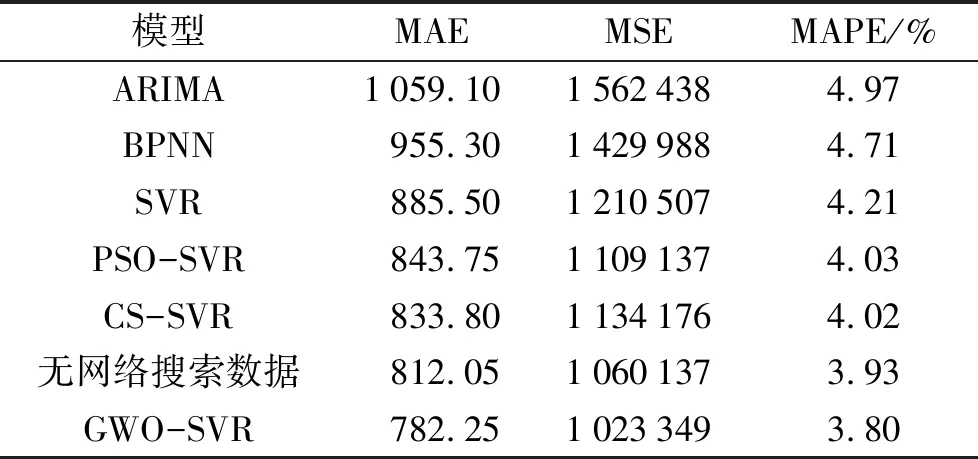
表5 九寨沟的预测性能比较

表5中可见， 与ARIMA模型相比， BPNN模型的MAE、 MSE和MAPE分别下降了9.80%、 8.48%和5.23%， SVR模型的MAE、 MSE和MAPE分别下降了16.39%、 22.52%和15.29%， 说明SVR对客流量预测问题更有效. 与SVR模型相比， PSO-SVR模型的MAE、 MSE和MAPE分别下降了4.71%、 8.37%和4.28%; CS-SVR模型的MAE、 MSE和MAPE分别下降了5.84%、 6.31%和4.51%; GWO-SVR模型的MAE、 MSE和MAPE分别下降了11.6%、 15.46%和9.74%. 表明参数优化提高SVR模型的预测精度， 且突出GWO算法的优越性. 总之， GWO-SVR模型表现最好， 证明将GWO和SVR结合起来的模型用于九寨沟客流量预测中是适当和有效的.

2.5 GWO-SVR模型的稳定性验证

为验证GWO-SVR模型的稳定性， 将该模型应用于四姑娘山景区中. 四姑娘山的搜索关键词有成都到四姑娘山、 四姑娘山、 四姑娘山攻略等.R阈值设为0.65， 最终搜索关键词如表6所示. 用昨日客流量、 时间特征信息、 最佳提前期搜索关键词的整体趋势作为输入变量， 用旅游客流量数据作为输出变量， 以2016年10月30日到2018年7月15日的624 d数据为训练集， 以2018年7月16日到2018年8月4日共20 d的数据为测试集， 建立GWO-SVR预测模型. 同样， 对比模型选择ARIMA、 BPNN、 SVR、 PSO-SVR、 CS-SVR和无网络搜索数据6个模型. 四姑娘山客流量原值与7个模型的预测值的对比结果如图2所示， 预测性能比较结果如表7所示.

表6 R > 0.65的四姑娘山搜索关键词

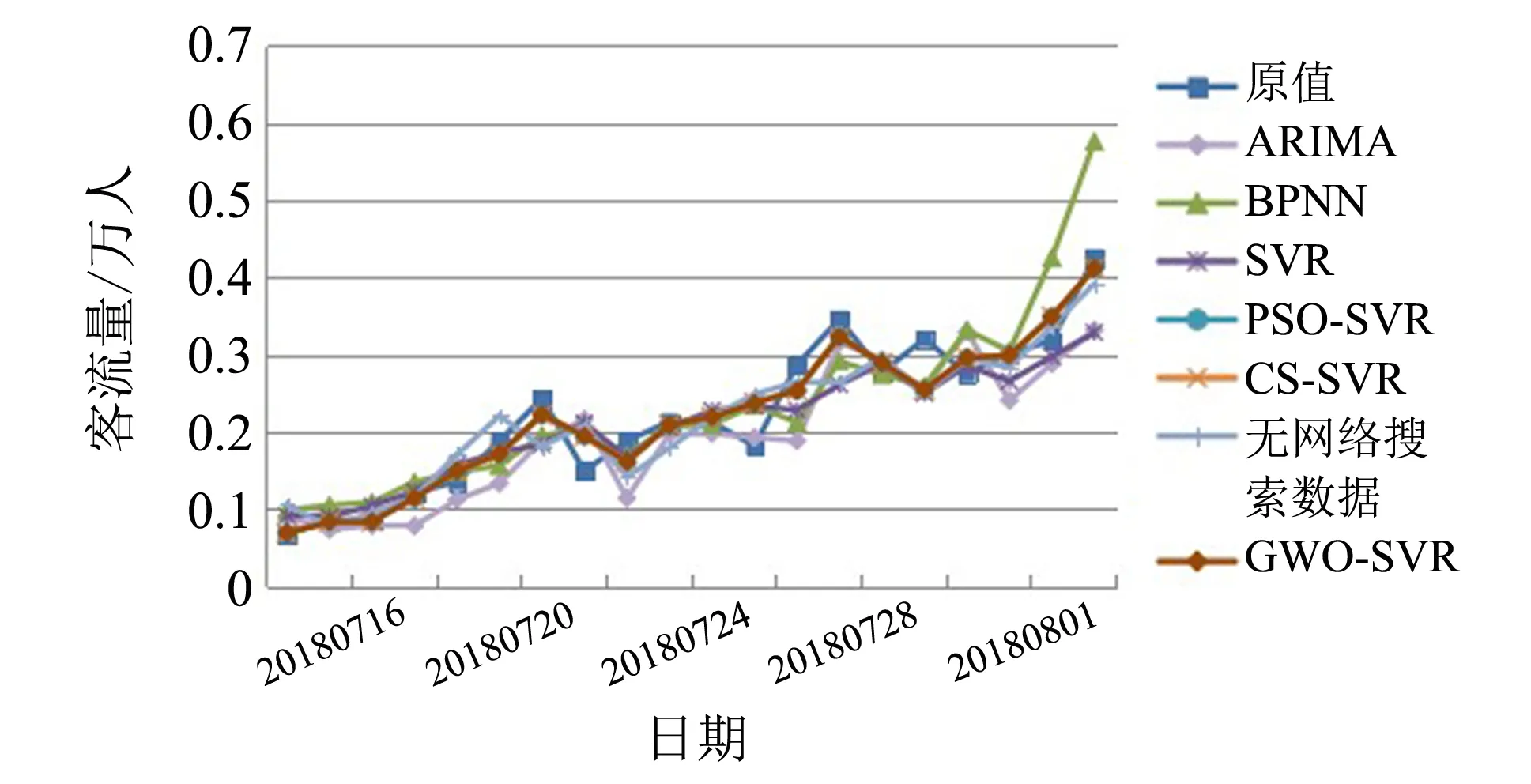
图2 四姑娘山客流量的原值与预测值Fig.2 Original and predicted tourist flow in Four Girls Mountain

结合表5和表7的结果， 发现ARIMA模型均表现最差， BPNN模型均表现第二差， 这说明在短期客流量预测中SVR模型优于ARIMA和BPNN模型. 表5和表7的结论是SVR模型优于ARIMA和BPNN模型， PSO-SVR、 CS-SVR和GWO-SVR模型优于SVR模型， GWO-SVR模型优于PSO-SVR和CS-SVR模型， GWO-SVR模型优于无网络搜索数据模型. 两个景区客流量预测结论是一致的， 表明GWO-SVR预测模型具有稳定性.

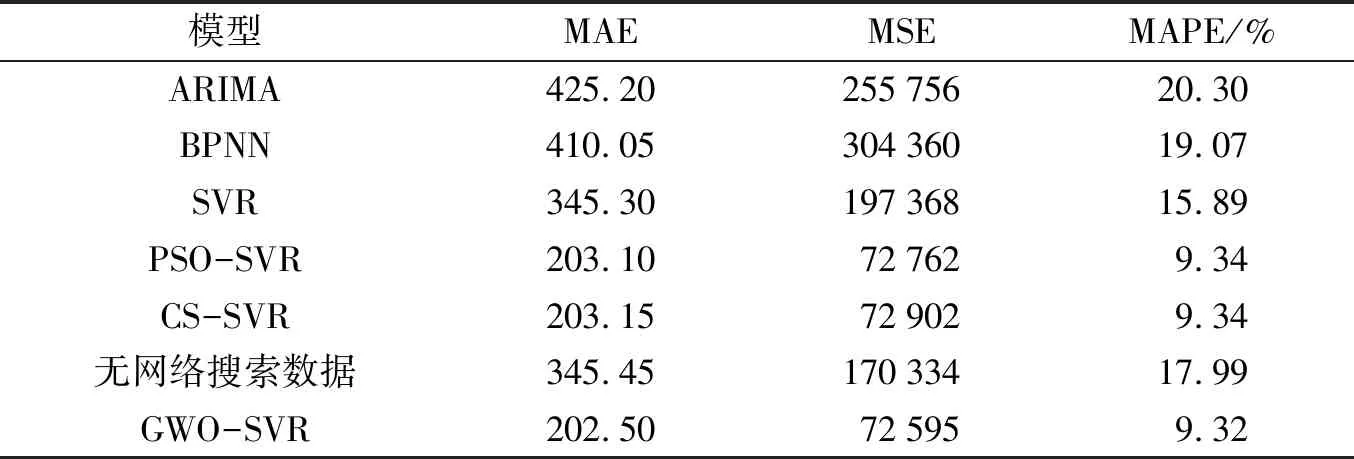
表7 四姑娘山的预测性能比较

3 结语

利用网络搜索数据建立GWO-SVR模型对九寨沟和四姑娘山两个景区的客流量分别进行研究. 实验结果表明： 首先， GWO-SVR预测模型在九寨沟和四姑娘山两个不同规模的景区中表现出泛化能力强、 预测精度高等优点. 其次， 网络搜索数据提高旅游客流量预测精度， 为旅游客流量预测研究提供新的数据来源. 最后， 在与ARIMA、 BPNN、 SVR、 PSO-SVR、 CS-SVR和无网络搜索数据6个模型的对比实验中， 发现本研究提出的GWO-SVR预测模型在各评价指标上都表现最优. 因此， GWO-SVR模型能较好地预测旅游短期客流量.