多参数融合的球磨机振动特征提取方法

陈慧明， 罗小燕， 熊洋

（江西理工大学机电工程学院,江西 赣州 341000）

球磨机是物料粉磨的关键设备，由于矿石内部结构的不均匀性及外部环境的变化，球磨机难以保持在最佳工作状态[1，2].在传统的破碎过程中，现场技术人员凭借经验来判断处理球磨机的内部运行状态，此基于手动操作的主观判断具有很大的局限性，且误差较大[3].目前，常用的方法是收集球磨机轴承，筒体，底座等的振动信号[4].根据振动信号与球磨机负荷之间的关系，确定球磨机的负荷状态[5，6].由于球磨机磨矿过程是非线性、大延迟、强耦合的复杂过程，单一特征无法完整的反映球磨机负荷状态的变化.因此，将多个特征联合表征球磨机负荷状态的研究成为趋势[7].

由于振动信号的时域和频域特性在不同负载条件下不同.文中利用了时域特性和频域特性的优点，并结合D-S证据理论，提出了一种振动信号特征提取的多参数融合方法[8].通过对实验数据的分析，结果表明所提出的多参数融合的振动信号特征向量能够有效的反映球磨机的负荷状态，具有一定的优越性.

1 振动信号时、频域特征提取

采用时域统计分析法，利用振动信号在时域上的波形、振幅、能量等信息，提取球磨机振动信号的有量纲特征参数（峰峰值、均值、标准差）和无量纲特征参数（峭度值、偏度值）[9-12].

振动信号的频谱特性可以有效地反映不同负载条件下振动信号的结构特征.通过统计方法描述振动信号的频域特性，以找到反映球磨机负载状态的频域特性[13-15].具体实现步骤分述如下.

1）线性差分方程用于表示观测数据的离散序列，如式（1）所示：

式（1）中，w（n-i）表示白噪声序列.

2）对式（1）中的线性方程进行Z变换，并输入白噪声的谱密度Pw（z）=σw2，变换可得式（2）所示:

3）将bi=0、z=ejw代入式（2）可得 AR 模型的功率谱估计值为：

式（3）中，P为AR模型的阶数；AR模型参数aj可以从观察到的数据序列的自相关序列中的计算导出.

2 多参数融合特征向量模型的构造

分别测量球磨机在不同负荷条件下运行过程中轴承的振动信号[16-18]，并分析各振动信号的时域和频域特征参数，构成N种球磨机负荷的振动信号的特征参数的一维矢量是：

假设在最佳负荷状态下球磨机振动信号的特征参数指标矢量为：

综合向量F和O可得mass函数向量：

同样，利用建立球磨机负荷特性预测模型的方法，可以建立n种负荷条件下l个振动特性参数的矩阵形式：

基于D-S证据不确定性推理，对M进行多特征参数融合以获得得到新的mass函数向量MN[19-20]：

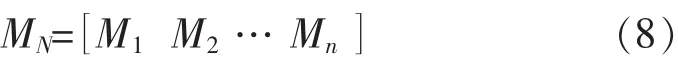
式（8）中，第j个元素为其表征是基于多振动特征参数数据融合的球磨机处于某种负荷状态的信度,且

3 实验结果与分析

对实验球磨机进行转速控制和能耗监测，并将传感器安装在球磨机两侧的支撑轴承座上进行振动信号采集，实验后的矿石进行筛分并分级处理[21].振动测试实验平台如图1所示.

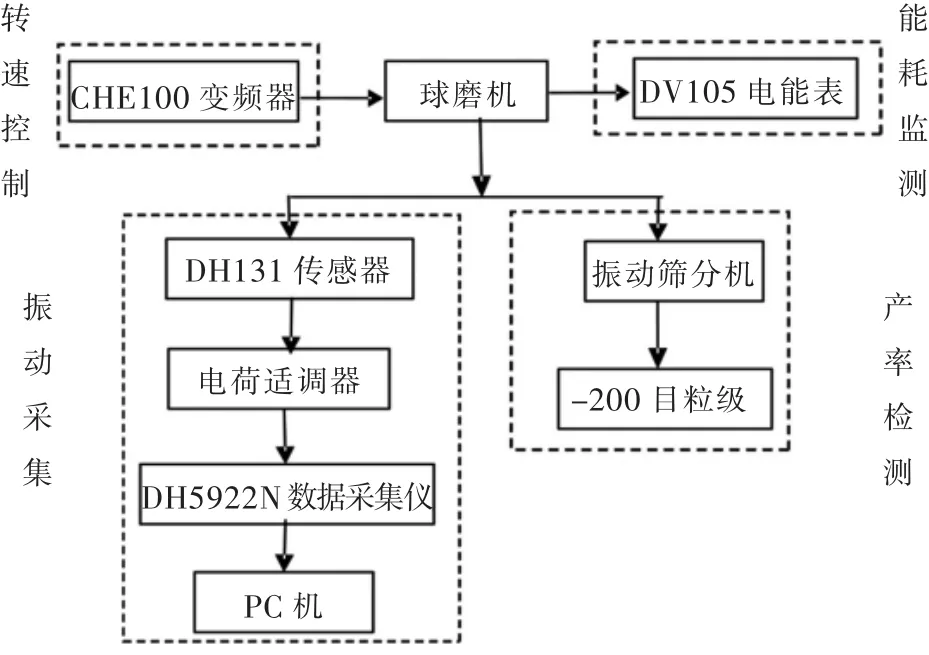
图1 振动测试实验平台框Fig.1 Block diagram of vibration test platform

填充率分别为 10%、20%、30%、40%和50%，料球比为0.6进行磨矿实验.对测取的振动信号进行时域、频域特征分析，如表1所列.

表1 振动信号时域、频域特征Table 1 Time domains and frequency domains features of vibration signal

从表1可知，不同负载振动信号的时域指标不同，可以很好地表征负载参数.时域指标峰峰值和均值在各个时段内发生变化，由于物料不断被磨细，振动信号的振幅减小，峰峰值和平均值更能反映振动信号的大小.时域指标方差、偏度和峭度更多的是描述振动信号的分布，随着磨矿的进行，其幅值也发生变化.不同负载的功率谱能量分布主要在频段一：1710～2848 Hz、 频段二：2188～3855 Hz、频段三：3855～5830 Hz和频段四：5830～8686 Hz中发生变化.

根据对大量实验磨矿后矿石筛分与功率之比可得，填充率30%为最佳负荷状态下球磨机振动信号的特征参数指标矢量.由表1中的数据可计算出将各个振动特征参数的mass函数值，结果如表2所列.

从表2可以看出，在时域特征内，偏度呈现出先减小后增加的变化，其他时域特征参数主要反映在数值的微小波动中，虽然在不同负载条件下信号时域特性不同，但特征差异不是特别明显；在频域特征内，不同负荷状态功率谱总能量存在不同，负荷参数为（30，0.6）时总能量最小，负荷参数为（50，0.6）时总能量最大.但是,负荷参数为（10，0.6）和负荷参数为（20，0.6）的总能量之间的差异却非常小，所以单独采用频域特征反映球磨机的负荷状态也可能存在误判.

为了解决单一特征值存在的缺陷，提高特征值反映球磨机负荷状态的准确性，利用D-S证据不确定性推理将振动信号的时域特征和频域特征进行数据融合，建立球磨机在不同负荷状态和振动特征参数之间的联系.融合计算出多振动特性参数的mass函数值，如表3所列.

由表3可知，负荷参数为（30，0.6）时多特征参数融合后的特征向量的能量值最小，负荷为（40，0.6）时融合后的特征向量的能量最大，且不同负荷参数下融合后的特征向量的能量值存在明显的差异.对比表2和表3可得，不同负荷参数下信号特征存在差异，但是在单一特征的情况相邻负荷参数间振动信号的特征差异并不显著，而多参数融合后的特征在不同负荷参数下差异非常明显.

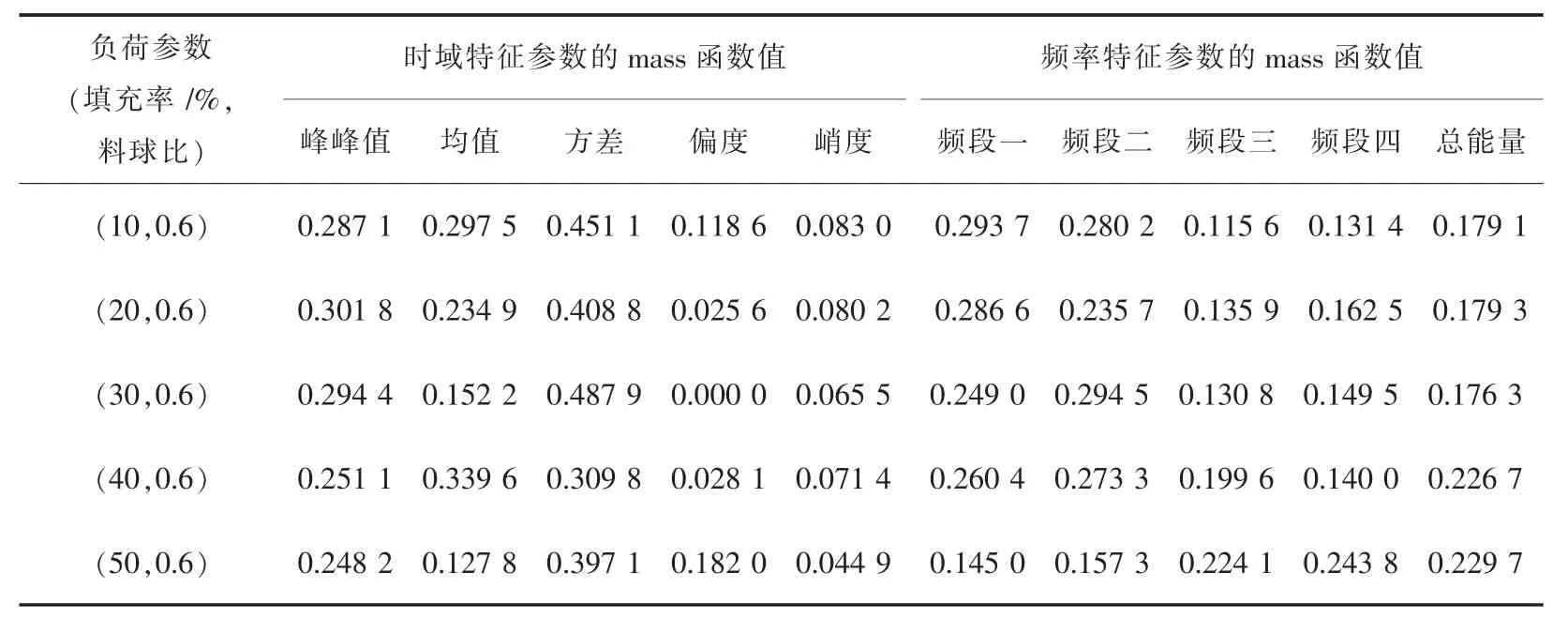
表2 单振动各时域、频域特征参数mass函数值Table 2 Mass function values of single vibration in time domains and frequency domains

表3 多特征参数融合后的mass函数值Table 3 Mass function value of multiparameters fusion

4 结 论

1）当填充率小于40%，在振动特征参数中，总能量、峰峰值、均值的mass函数值最大，对负荷预测贡献率较大.当填充率达到50%，有量纲时域特征的贡献率最小；随着填充率的增大，方差、频段一和频段二的mass函数值呈减小趋势，贡献率减小，偏差、频段三和频段四呈增大趋势，贡献率增大.

2）多参数融合后的各填充率下最大mass值的振动特征参数都不同，更加明显的表征不同负荷状态，避免了依靠单个特征建立特征向量模型的不准确性，为球磨机负荷的准确预测提供了新的方法.