思维可视活动突破“图形与几何”学习障碍的对策

浙江省义乌市东河小学 陈晓倩

有关“思维可视活动突破高段学生‘图形与几何’学习障碍的对策研究”课题研究，国内外有关“思维可视化的相关研究”、“思维导图的研究”的课题比较多，但对思维可视化与思维导图的相关研究重教学应用的理论研究，所以，我觉得有必要在此基础上找到一个新的研究点，通过思维可视活动的设计与实施的研究，深化出一些更具可行性和操作性有效突破高段学生“图形与几何”学习障碍的策略，能在“图形与几何”教学中更好地借鉴与实施。

可视不是单纯意义上指用眼睛观察，而是借助观察、触摸、绘图、演示等直观的形态，通过感知、想象、感受、直观意识行为理解知识建构的过程。而思维可视活动是指改变以往在“图形与几何”教学中强调答案的活动，设计在思考视域中通过绘图导学、构图活动，从而突破高段学生“图形与几何”学习障碍，提升学习“图形与几何”的效率。

一、遇到的问题与困惑

作为《数学课程标准》的四个领域之一，“图形与几何”是在传统意义上的几何内容基础上发展起来的，学生在解题时经常会遇到不会分析图，不会把思考方法和思考路径呈现出来，束手无策。当学生不会做题时，问他在这几分钟进行了哪些思维活动？不少学生总是回答：不知道怎样去思考分析。我也对小学数学六年级期末检测卷中“图形与计算”考查板块进行了调研。六年级期末检测卷“图形与计算”得分情况调查表

?

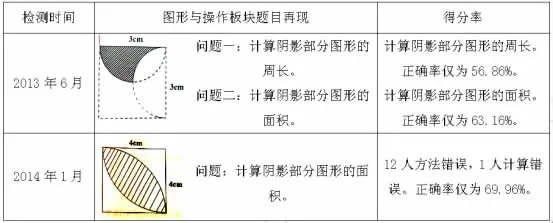
从以上调研的数据引发我们深入思考，是什么成了学习“图形与几何”的障碍？

二、对问题产生的原因分析

经过一段时间的反思分析，我发现在“图形与几何”教学中，主要是知识表征背后的思维规律、思考方法、思考路径不能正确表示及呈现出来，成了学习“图形与几何”的障碍。在教学中主要存在以下问题：

1.缺少对图形表征的感知活动

不少学生总是对图形特征的认识比较表面、片面，各种概念（如周长、面积和体积）没有真正区分，图形间的关系更是不明确。教学中，教师不重视对实物的观察、触摸、搭建，总觉得这费时费力，收效不大，喜欢用文字表征法，对学生而言是抽象、难掌握、难理解的，缺少了运用符号和实物来描述知识和知识结构的可视化活动。

2.缺乏图形运动变化的演示活动

在我们的图形教学中总是受年龄特征制约了小学生对极限思想的深刻理解，教学中淡化了对极限思想的渗透。如直线、射线、角的边、平行线的长度等等它们都是可以无限延伸的，拉动平行四边形的面积变化规律，圆面积可以转化成长方形等。教师因缺乏图形运动变化的演示活动来有效说服学生，使我们的图形教学陷入尴尬。

3.缺少体现过程理解的呈现方式

面对图形的概念、公式等所谓的“死知识”，我们对材料间的关系把握不准，随意设定教学目标，造成过程理解的缺失，这样一来，学生掌握的永远都是“死知识”，解决问题时使用的永远都是“死方法”。

我们认为在“图形与几何”教学中可以通过“思维可视活动”进行构建的。第一，它符合小学生的思维发展的需要，小学生对几何图形的认识处于直观几何阶段，通过多种感知活动，促进几何知识的内化；第二，它有助于小学生空间观念的培养，关注了几何直觉和推理能力的发展。第三，它切合小学生过程理解的需要，“思维可视活动”把抽象的“图形与几何”变得直观、形象，易接受的活动，促进过程理解。可见“思维可视活动”在“图形与几何”教学中的重要性。

鉴于以上的思考，我进行了“思维可视活动突破‘图形与几何’学习障碍的对策研究”这一思考。目的就是通过“思维可视活动”把“图形与几何”教学中把原本看不见的思维结构、思考路径以及方法借助绘图导学、构图活动、用图练习呈现出来，使其过程理解清晰可见，进而提升小学生学习“图形与几何”的效力。

三、思维可视活动突破“图形与几何”学习的措施与方法

突破高段学生“图形与几何”学习障碍，可采取“思维可视活动”的教学理念，运用绘图导学、构图活动、画图练习为载体

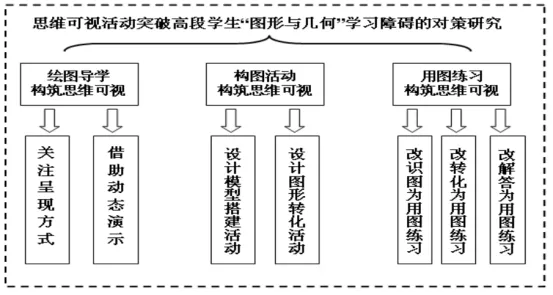
策略一：绘图导学构筑思维可视——关注“知识点”转变为关注“思维层”

所谓“绘图导学构筑思维可视”，就是克服在图形表征认识上的表面与片面，通过绘图导学把思维灵活地呈现出来，通过研究变关注“知识点”引向为关注“思维层”。

（一）关注呈现方式

1.图示呈现

图示呈现是指在“图形与几何”教学中通过以图示替代文字把蕴含的方法、思想呈现出来的可视化教学方式。如教学平行四边形、三角形、梯形、圆的面积时，只提供一个标有数据的图形，让学生借助已有经验，用图示的方式表示自己的解答方法，再进行反馈交流。

操作流程：

2.图文配合呈现

在研究中，我们要求学生在理解题意时，把无形思考过程改用图文配合的方式表示出来，这样就会逼着学生去思考，从而提升学生解决问题的策略。

具体操作：

（二）借助动态演示

1.演示图形无限延伸活动

小学几何概念中有许多概念是具有无限性的，它们只是存在于人脑的想象之中，是人脑抽象的结果。我们要改变只是借助想象来体验，设计可以让学生可操作的动态演示真正理解无限延伸。

2.演示公式极限探索活动

探索公式推导过程——在公式推导过程中设计演示极限探索活动，借助几何画板展示“无限”的过程，沟通公式间的联系——本课题研究中我们把单元整理中带有规律性的知识，改用动态演示沟通知识，使知识条理化、系统化。

策略二：构图活动构筑思维可视——关注“单纯操作”转变为关注“思维体验”

所谓“构图活动构筑思维可视”是指能由实物的形状呈现几何图形，能根据条件做出模型或展出图形的活动，加强学生对图形的表征、性质的理解。

（一）设计模型搭建活动

在低段教学图形及其特征时，都是从生活中的实物抽象出图形的特征，但到了高段教师还是采用实物抽象出图形的特征。其实学生对模型是非常感兴趣的，现在的孩子都是玩积木长大的，因此我们在进一步认识图形特征时，尝试模型搭建活动，引导学生把自己了解的图形特征通过模型展示出来。

操作流程：

1.用学具搭建

数学教材给每一位学生配备了一套数学学具，在认识图形特征时，变只用眼睛观察这单一形式，为可以动手操作的模型搭建活动，这样的活动把学生思维通过学具搭建展示出来，能让每一个学生积极参与。

具体操作：

教学《圆柱认识》一课。设计这样学具搭建活动：利用学具里圆柱，先想一想你打算怎样用最少的彩纸把这个圆柱包起来？（纸不能重叠，不能浪费哦！）展示成果，汇报交流。

2.用意想搭建

我们改常规操作活动为意想搭建活动，通过在大脑中想象搭建，再把思维过程通过画图或表述的形式表示出来。

具体操作：

教学《长方体认识》一课，设计这样的活动：有10 厘米的小棒8 根，8 厘米的小棒4 根，4 厘米的小棒4 根，2 厘米的小棒3根。请你选择合适的小棒进行搭建长方体。先写出你的选择方案，想象搭成的长方体的样子。（可以用画图或表述展示思维成果。）

（二）设计图形转化活动

1.图形到实物的转化

重视从生活中的实物抽象出图形过程，但是将图形及其特征应用到生活中去的比较少，我们可以从这方面进行设计。

具体操作：

当一个建筑工人为一个修理厂建造长方体底座时，要判断底座表面的形状是否为长方形。你能为他设计一种判断的方法？画出你的想法。

2.二维到三维的转化

三维和二维的转化，即从立体转换到平面，反过来由平面转换到立体。对于这一点，在以往的教学中不够重视，也没有设计这样活动。要体现这一过程，使二维与三维间的转化过程变成可视的活动，培养学生的空间观念。

策略三：用图练习构筑思维可视——关注“结果”转变为关注“过程理解”

所谓“用图练习构筑思维可视”是指在解决“图形与几何”实际问题时，我们改识图为用图呈现，改转化为用图练习，改解答为用图练习，在不一样的解决问题中展现学生思维过程，培养学生对“图形与几何”问题解决的能力。

1.改识图为用图练习

在教学中要利用标准图形，我们可以设计这样的画图练习。如：这两幅图你想到怎样的基本图形，请用图呈现。

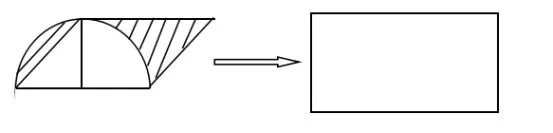
2.改转化为用图练习

转化是图形与几何教学的核心本质。在练习设计时，注重转化意识的培养，因此我们改转化意识为用图练习，培养学生的转化意识。如：用图画出你的想法？

3.改解答为用图练习

通过改列式为用图练习，要求学生不列算式，只用图来表示数学问题。这样的练习设计，重过程而轻结果，能充分地暴露学生的想法，培养学生遇到难题时，会运用图策略来解决问题的习惯，提高学生对“图形与几何”问题解决的能力。

总之，通过“思维可视活动”，激活学生学习“图形与几何”的兴趣，突破“图形与几何”学习障碍。学生能灵活借助“思维可视活动”提升数学思维，提高学生的几何直观能力和解决问题的能力。转变教师的教学方式，寻找优化“图形与几何”教学的有效策略，提高教师“思维可视活动”的设计能力。