低围压下颗粒形态对软黏土抗剪强度影响的离散元分析*

赵 洲 张 鹏 宋 晶③④ 李 学 李志杰 黄伟标

( ①中山大学地球科学与工程学院 广州 510275)

( ②中交第四航务工程勘察设计院有限公司 广州 510230)

( ③广东省地球动力作用与地质灾害重点实验室 广州 510275)

( ④广东省地质过程与矿产资源探查重点实验室 广州 510275)

0 引 言

近年来，吹淤造陆成为人工陆域形成的重要手段，广泛用于工业、交通和房屋的建设。软黏土作为吹填淤泥的主要成分，由于其压缩性高、强度低等特性，易造成地基沉降等不良地质现象，极大影响了吹淤造陆工程的稳定性和安全性。软黏土颗粒大多呈片状水平成层结构，研究软黏土颗粒形态对于其力学特性和变形机理具有重要的意义。

在考虑颗粒形状的数值研究中:孔亮等( 2011)运用二维离散元对砂土进行了直剪试验等室内试验的模拟，研究了颗粒形态和抗剪强度之间的关系。Asadi et al. ( 2018) 利用PFC3D模拟不同形状的沙土橡胶混合颗粒，并进行一维压缩试验，研究了颗粒形状对混合料压缩性和抗剪强度的影响。乐天呈等( 2018) 借助离散元软件分析了颗粒级配和形态等微观结构的变化对砂土宏观力学的影响，但并未从细观水平揭示其变形机理。周伦伦等( 2017) 引入滚动阻矩模拟颗粒形态的作用，但其方法仍与颗粒实际状态存在差距。同时，颗粒形状也影响了剪切带 的 形 成 与 发 展( Gu et al.，2014; Garcia et al.，2019)

已有研究主要集中于砂土等无黏性土，针对黏土颗粒的研究尚不多见。与沙土不同，黏土颗粒主要为片状成层分布，且颗粒之间存在着黏结作用( 刘治清等，2017) 。Yao et al. ( 2003) 在对黏土的一维固结试验进行离散元模拟时，采用六面体颗粒试样，对其在微观和表观的力学行为进行探讨。常在( 2008) 使用PFC2D模拟黏土试样双轴试验，研究了片状颗粒单元的长度、弯度和倾角等几何性质对抗剪强度指标的影响。陈建峰等( 2010) 利用离散元模拟黏性土的双轴试验，得出抗剪强度指标与土颗粒间细观参数的线性关系。

基于通过研究土体的微观结构进而解释宏观性质的思路，将图像处理技术广泛用于软黏土的研究中。利用扫描电镜揭示土体的二维微观结构，从而获取颗粒细观参数，为建立PFC 颗粒流模型建立了基础( 周健等，2006) 。由Cundall 提出的离散单元法被广泛应用在岩土领域，椭圆、椭球、蛋形以及多边形、多面体等颗粒单元先后被学者用于颗粒形状影响的数值模拟研究。Abbireddy et al. ( 2015) 提出等效球度概念，并利用CT 扫描研究片状颗粒在剪切过程中的形态变化，并探讨了颗粒形状对抗剪强度的影响; 王学滨等( 2018) 基于黏性土的一维压缩试验，利用数字图像法揭示了剪切带的演化规律及破坏机制。郑博宁等( 2019) 通过CT 技术对砾石边界予以识别，并进行三维重构用于数值模型的建立。

对于三轴试验的颗粒流离散元数值模拟，国内外研究主要集中在无黏性土等材料。本文主要对黏性土进行研究，以颗粒球度和凹凸度作为指标，建立球体和片状颗粒模型，模拟分析颗粒形状对黏土试样抗剪强度的影响，并从颗粒位移和颗粒旋转等细观层面揭示其影响机理。

1 黏土颗粒模型分析

1.1 颗粒形状定量表征

为揭示颗粒形状对力学行为影响，需先对颗粒形状进行定量表征，颗粒材料的变形首先是由颗粒移动引起，颗粒移动包括颗粒的平移和翻转两个过程，与颗粒形状密切相关( 孔亮等，2011) 。颗粒形状的描述可分为两个尺度，一是颗粒整体形态上的尺度，定义为球度S =，其中，L、I、B 分别为颗粒的长轴、中长轴和短轴; 二是颗粒边界的突起程度，定义为凹凸度F = Af/AS，其中，Af为最大内接圆面积，AS为与投影轮廓同周长圆面积。黏土颗粒多呈球状或片状，且轮廓形态不规则，因此通过球度和凹凸度能较好反映颗粒形态对力学性质的影响。

1.2 试验材料

本文原状土样取自深圳某填海工程，为灰黑色饱和软黏土，土中大量的高岭石、伊利石等黏土矿物。图1a 为软黏土在天然状态下的SEM 图像，由图可见软黏土颗粒排列相对松散，颗粒多为片状成层分布，黏粒之间以边－面、面－面接触为主，形成多孔蜂窝状结构或团粒絮凝结构。利用PCAS 软件对SEM 图像进行二值化处理，将黑度图像转化为黑白图像，如图1b 所示，其中黑色部分为土颗粒，白色部分为孔隙。对图1a 进行局部放大，可观察到形状近似圆和矩形的两种片状颗粒( 图1c、图1d) 。统计颗粒方向角分布频率如图2 所示，由图可知天然状态下黏土颗粒在各角度区间分布均匀，无定向性，由此可见原状土在天然沉积历史中未形成稳定的定向排列结构。统计颗粒的凹凸度形状特征值如图3所示，颗粒凹凸度近似呈正态分布，在0.2 ～0.4 的范围内较为集中，说明天然状态下，软黏土颗粒形态偏离圆形较高而更为狭长，这与原状土冲积和沉积历史有关。

2 数值模型建立

离散元法( DEM) 自提出以来，已在研究颗粒材料的力学特性方面得到广泛运用，颗粒流( PFC) 软件基于离散元法，交替执行牛顿第二定律和力－位移定律，其中，牛顿第二定律运用于单个颗粒上，以判断每个颗粒在合力作用瞬间的运动状态; 力－位移定律作用在各个颗粒的接触上，以实现接触力的迭代更新。

图1 黏土颗粒微观Fig. 1 Microscopic image of clay particles

图2 黏土颗粒方向角频率Fig. 2 Directional angular frequency of clay particles

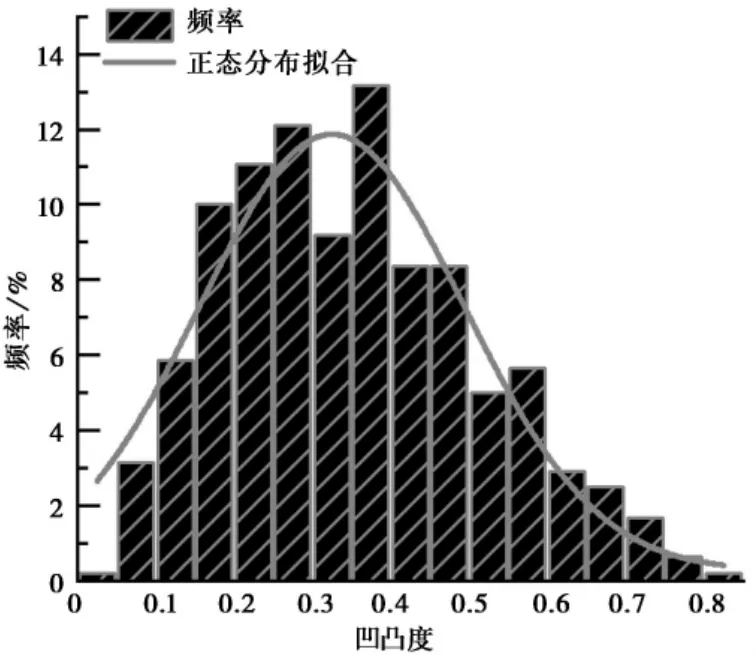
图3 黏土颗粒凹凸度频率Fig. 3 Concave-convexity frequency of clay particles

2.1 簇体颗粒构建

通过扫面电子显微镜来获取土体微观图像，本文研究颗粒的球度和凹凸度对抗剪强度的影响，把颗粒的形状归为4 类: 球体单粒及圆柱体、正方体，长方体的片状簇体。由于研究低围压下软黏土的力学行为，不考虑颗粒破碎情况的发生，因此采用clump 命令构造的三维图像，并视团粒及其表面结合水为一个整体，团粒之间的相互作用以黏结力为主，而忽略范德华力和双电层力的影响，采用PFC中的接触黏结模型来模拟软土颗粒间的接触力学行为最为适宜。统计每种颗粒模型的球度和凹凸度见表1，可以看出，球体与其他3 种片状簇体的球度相差较大; 而3 种片状颗粒之间的球度差别不明显，但凹凸度差异较大。因此通过比较球体与片状颗粒来探究球度对抗剪强度的影响，通过比较圆柱体、正方体和长方体的片状团簇颗粒来探究凹凸度对抗剪强度的影响。

表1 黏土颗粒形状及参数Table 1 Shape and parameters of clay particles

2.2 颗粒级配

模拟真实三轴试验建立模型，PFC 计算的最大时间步长与模型中颗粒质量有关，如果使用实际的颗粒大小，模拟时间往往很长。因此有必要对颗粒粒径进行一定倍数放大，以增加最大时间步长，提高计算效率。基于以上论述，对试验级配曲线中进行适当修正，并对粒径等比例放大。试样级配曲线如图4 所示:

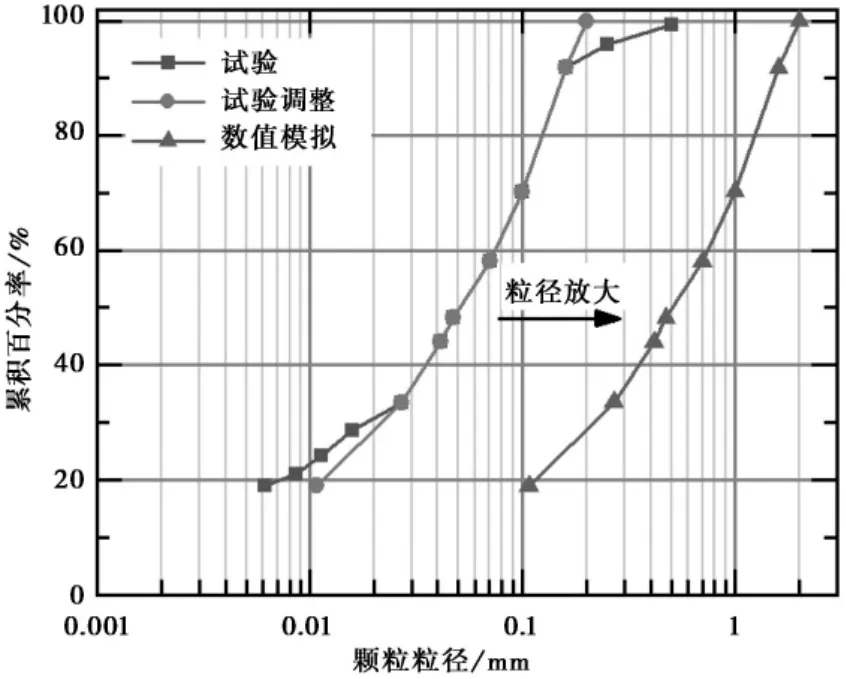
图4 颗粒级配曲线Fig. 4 Grain size distribution curve

2.3 细观参数选取及三轴试样建立

参考已有黏土数值模拟文献( 高彦斌等，2009;陈建峰等，2010) ，最终确定一组最能拟合室内三轴试验结果的细观参数，各细观参数见表2。

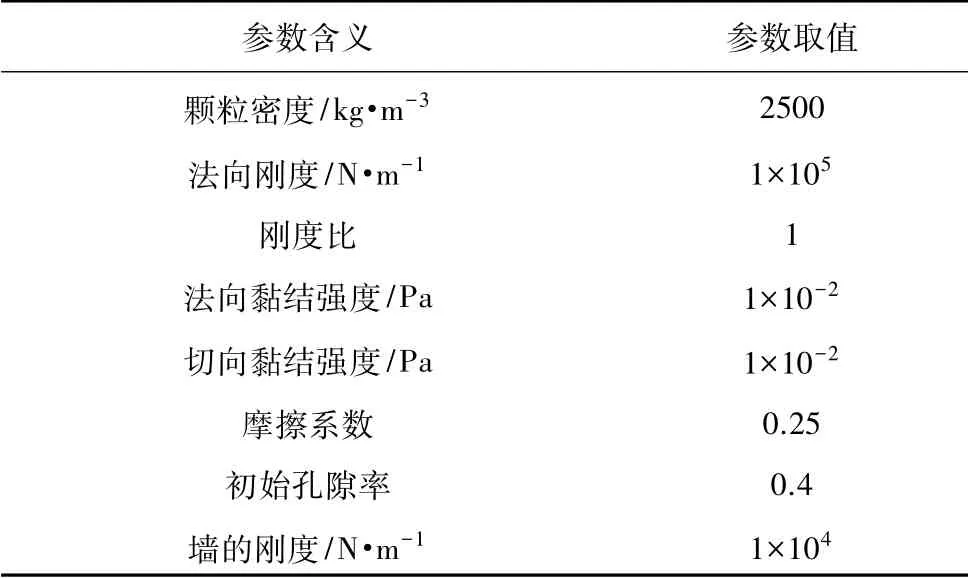
表2 颗粒流数值模拟参数Table 2 Numerical simulation parameters

三轴数值模型的建立与室内试验一致，试样为高度100 mm，底面直径50 mm，上下水平刚性墙体作为加载板，施加轴向压力，侧面边界墙体用于施加围压，并使用伺服机制控制，以实现其约束恒定。颗粒在满足边界效应的基础上，按级配曲线分布，利用半径扩展法达到预期孔隙率，试样模型见图5。本次模拟采用应变控制加载方式，加载速率与室内试验保持一致，当轴向应变达到20%时，停止加载并记录信息。三轴实验的数值模拟设置3 组围压:100 kPa、200 kPa 和300 kPa。在试验中记录试样的轴向应变和应力，用于力学性质的分析; 并采集颗粒位移和旋转信息，以反映其内部微观结构。

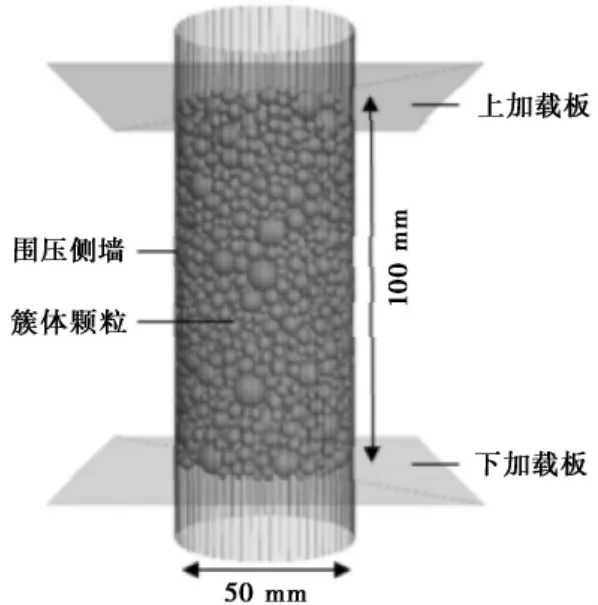
图5 三维离散元数值试样Fig. 5 Numerical specimen of the three dimensional DEM

3 三轴试验离散元模拟

3.1 应力与应变关系

4 种颗粒形状的黏土试样在不同围压条件下的应力与应变关系曲线如图6，由图可知:

( 1) 3 种片状的黏土试样均表现出一定程度的应变硬化特性，而球体颗粒试样表现出轻微的弱化现象。分析其原因在于片状颗粒的球度和凹凸度均远小于球体颗粒，其颗粒形状愈不规则，颗粒间的咬合作用愈明显，因此所能达到的峰值偏应力也最大。

( 2) 低围压下，4 种颗粒形状的黏土试样的初始弹性模量差别不显著; 当围压提高到300 kPa时，片状颗粒的初始弹性模量比球体颗粒有明显提高。其原因表现在: 球体颗粒的球度比片状颗粒平均高出33%，而在剪切初期，颗粒球度对试样的初始弹性模量影响显著，球度越小，初始弹性模量越大，因此球度对应力－应变曲线初始形态起到控制作用。

( 3) 小应变下，3 种片状颗粒的应力－应变曲线斜率相近。随着应变进一步增大，曲线峰值出现明显差异，颗粒形状为球体、圆柱体、正方体、长方体的黏土试样的偏应力值依次提高。究其原因在于随着轴向应变增大，片状颗粒凹凸度的作用逐渐发挥明显，并成为影响试样抗剪强度的主要因素。

3.2 初始弹性模量

图6 黏土颗粒试样应力－应变关系Fig. 6 Stress-strain relationship of clay particle samples

对4 种黏土试样初始弹性模量的研究，取轴向应变为1%时进行分析。绘制颗粒球度S 与初始弹性模量E 关系如图7 所示。

由图可知，初始弹性模量随着颗粒球度的减小而逐渐增大，且围压越大，增长率越快。其表现在于:初始加载阶段，黏土颗粒间孔隙较大，密实度不高，未形成稳定的絮凝结构，而球度越大的颗粒越易产生相对位移或转动，因此球体颗粒的初始弹性模量最小。这与Ha et al. ( 2017) 对颗粒材料进行实际试验所得的结论一致。

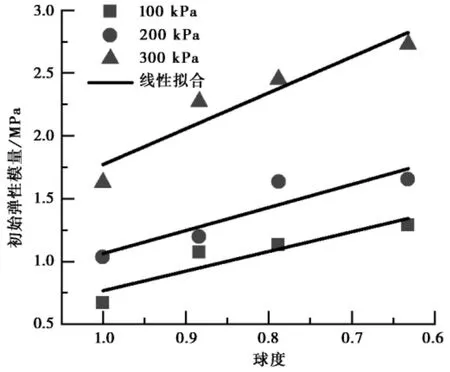
图7 球度与初始弹性模量关系曲线Fig. 7 The relationship between sphericity and initial modulus of elasticity

3.3 抗剪强度

在应力－应变图中，当曲线达15%轴向应变时，认为土体发生剪切破坏。根据莫尔－库仑理论，绘制强度包络线并计算出3 种片状颗粒模拟黏土试样的抗剪强度指标: 黏聚力c 和内摩擦角φ。分析凹凸度F 与黏聚力c 和内摩擦角φ 的关系( 图8) 。

凹凸度F 与黏聚力c 呈线性关系，可拟合为线性方程:

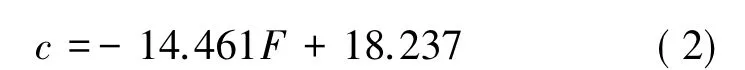
凹凸度F 与内摩擦角φ 进行线性拟合后的方程为:

图8 凹凸度与抗剪强度指标关系曲线Fig. 8 Relation between concavity-convexity and shear strength index

由图8 可知: 随着凹凸度减小，试样的抗剪强度指标逐渐增大，且黏聚力的增长斜率远大于内摩擦角，分析其原因在于: 轴向应变增大过程中，颗粒之间接触紧密，凹凸度的作用逐渐体现，颗粒凹凸度越小，形状越不规则，粒间的咬合程度加大，在宏观上表现为试样的抗剪强度提高。另外，凹凸度小的颗粒形状更为细长，接触面积更大，表现出颗粒之间的黏聚力明显提高，所以凹凸度对黏聚力影响远大于对内摩擦角的影响。

4 细观机理分析

4.1 颗粒位移

由应力－应变关系( 图6) 可知，当围压为100 kPa 时，黏土颗粒形状对试样的抗剪强度的影响较为显著。图9 为100 kPa 围压下，轴向应变15%时，4 种形状的黏土试样在剖切面上的位移图，由图9 可知:

图9 颗粒位移场分布图Fig. 9 Particle displacement field ε=15%

( 1) 当轴向应变达到15%时，4 种形状黏土颗粒的位移具有相似的规律: 试样上下端靠近加载板处颗粒的轴向位移较大，在宏观上的表现为试样的轴向压缩; 而试样中部颗粒的轴向位移减小，侧向位移增大。对于图9 中3 种片状试样，试样中部出现明显的侧向位移三角区，在宏观上的表现为试样的侧向鼓胀。如图10 所示，剪切初期，片状黏土颗粒的接触类型主要以边－边和边－面接触为主，颗粒间存在较大孔隙; 随着剪切进行，其接触逐渐转化为更稳定的面－面接触，颗粒方向趋于水平向。

( 2) 对比球体颗粒和片状颗粒的位移图发现，片状颗粒试样破坏时的剪切带比球体颗粒更为明显，呈现出规则的X 型分布。3 种片状颗粒的剪切带宽度和位移场密度都随凹凸度的减小而逐渐减小。这是由于剪切后期，颗粒凹凸度的作用逐渐明显:在密实状态下，颗粒凹凸度越小，颗粒之间的嵌合连结越为紧密，颗粒之间发生相对移动更困难，试样局部破坏范围也更小。

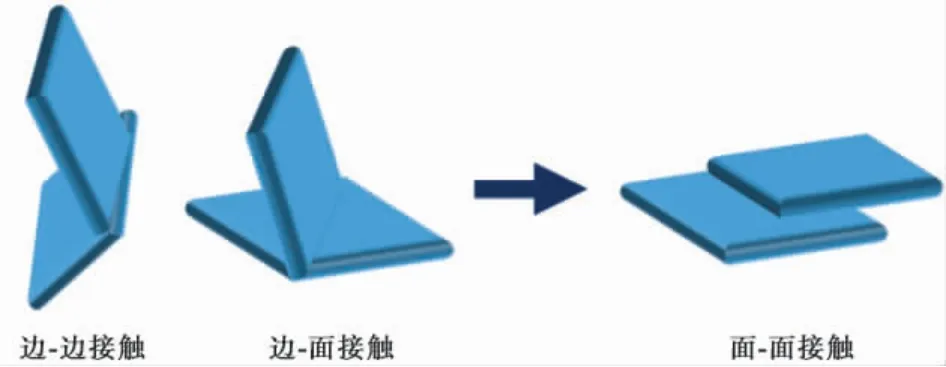
图10 片状黏土颗粒的接触类型变化Fig. 10 Contact type change of flaky clay particles

4.2 颗粒旋转

图11 、图12 为围压为100 kPa，轴向应变分别为1%和15%时，4 种形状的黏土颗粒试样在剖切面上的角速度云图，对比图11、图12 可看出，剪切初始阶段( ε = 1%) ，球体颗粒相对于其他3 种片状颗粒更容易发生自转，其范围集中在试样中部，而片状颗粒的角速度差异不明显。在剪切破坏阶段( ε =15%) ，球体颗粒转速有大幅提高，旋转范围从中部扩大到试样整体。另外，片状颗粒的旋转角速度也呈增大趋势。从图12 可以看出，圆柱体、正方体、长方体颗粒的转动速度依次减小。球体颗粒由于其球度较高，颗粒接触分布不均匀，更容易发生相对位移和转动; 而对于片状颗粒，其中长方体颗粒凹凸度最小，颗粒形状更为细长，由于其咬合作用高导致粒间结构更稳定，因此长方体颗粒旋转量也最小。而相同形状的颗粒旋转速度随剪切过程变化幅度不明显，可推测与黏土颗粒黏结强度较大有关。

图11 ε=1%时颗粒角速度云图Fig. 11 Grains angular velocity diagram at ε=1%

图12 ε=15%时颗粒角速度云图Fig. 12 Grains angular velocity diagram at ε=15%

5 结 论

( 1) 4 种形态的黏土颗粒中，球体颗粒的球度远大于其他3 种片状颗粒，而圆柱体、正方体和长方体片状颗粒的球度相差不大，凹凸度依次减小。

( 2) 根据三轴试验模拟结果，黏土试样均有一定的应变硬化特性，加载初期，颗粒球度对初始弹性模量影响突出; 随加载进行，凹凸度的作用逐渐凸显，影响试样抗剪强度指标，且对黏聚力的影响大于内摩擦角。

( 3) 试样发生破坏时，颗粒的球度越小，剪切带越为明显，凹凸度越小时，剪切带宽度、位移场密度和颗粒旋转速度都有所增大。

(4) 建议进一步对黏土颗粒高压变形及破碎情况进行研究，考虑排水条件的影响，并考虑颗粒表面双电层力和范德华力作用，以期获得更为真实的黏土力学模型。