强震作用下均质岩质边坡动力响应的振动台模型试验研究*
詹志发 祁生文 何乃武 郑博文 葛传峰
( ①中国公路工程咨询集团有限公司 北京 100089)
( ②中国科学院地质与地球物理研究所,中国科学院页岩气与地质工程重点实验室 北京 100029)
0 引 言
我国地势西高东低,山地、高原和丘陵约占陆地面积的67%,因此也是滑坡广泛分布的国家。近年来,由于地震灾害的频发,强震诱发边坡失稳作为地震中最为常见的次生灾害,致使我国的地震滑坡灾害数量位居全世界之首。据文献资料统计,在20 世纪之前,已知发生在我国4.5 级以上地震就有5000余次( 丁彦慧,1997) 。Keefer( 1984) 对1811 ~1980年间的地震诱发滑坡进行了研究,并整理了1958 ~1977 年《United States Earthquake》刊登的300 个历史地震数据,提出了震级与滑坡分布范围的公式,认为当地震震级大于4.0 时便可触发地震滑坡灾害;而在强震大于6.0 时,尤其是超过7.0 时,地震诱发的滑坡灾害将尤为突出和显著。仅2008 年5 月12日发生在四川汶川的8.0 级地震,就造成了8.7 万余人死亡,30 余万人受伤,触发了数以万计的地质灾害点,其中绝大多数为滑坡灾害,直接造成了严重的生命和财产损失( 许强等,2009) 。
国内外许多大型工程建设于构造活动带,山高坡陡。例如,建在雅砻江上的锦屏一级水电站的自然高边坡就高达1300 多米,强地震诱发的山体地质灾害往往成为威胁这些工程安全的重要隐患。因此,边坡地震稳定性的研究近年来是相关领域国内外学者的研究热点。动静荷载对于边坡变形破坏形式的影响差异甚大,很多学者对于边坡静力条件下的稳定性开展过诸多研究,但是边坡在动力加载时的机理研究还很欠缺( 祁生文等,2007) 。地震荷载是工程中常见的动荷载形式之一,地震动荷载在岩体中传播,对岩体中的硐室、边坡以及基岩等都会造成相当程度的灾害。
对地震边坡稳定性问题的真正认识则要追溯到1936 年,Mononobe et al.( 1936) 最早认识到坝坡是变形体; Hatanaka( 1952,1955) 通过对土质坝坡的研究,发现在地震动力作用下坝坡的形变是以剪切变形为主; Ambraseys( 1960a,1960b) 在此基础之上,进一步将剪切楔法应用到平面形态为梯形的土质坝坡中。这一时期,研究者们不仅在土质坝坡地震稳定性分析方面进行了大量的研究,同时也对边坡在地震动力作用下的动力响应问题开展了研究,Idriss et al. (1967) 首次对于单面土坡的动力响应问题进行了研究。在我国西南地区由于地形上多山高谷深且地震活跃,岩质边坡稳定性问题尤为突出,在国内较早研究岩体边坡动力问题的是王思敬(1977) 。
此后,国内对这一研究也逐步在深入,学者采用有限元方法对二滩工程和三峡船闸等边坡工程动力稳定问题展开了计算( 何蕴龙等,1998) 。国内开始逐渐注意到岩质边坡动力响应规律性研究的重要性,其研究也在逐步深入。祁生文( 2002,2006; 祁生文等,2003) 较为系统地研究了岩质边坡动力响应规律,许强等( 2010) 、董金玉( 2010) 、杨国香( 2011) 、邹威等( 2011) 、黄润秋等( 2013) 、刘汉香等( 2013) 、范刚等( 2015) 、Fan et al. ( 2016; 2017a;2017b) 、李果等( 2016) 、Yang et al. ( 2018) 也都对均质岩质边坡动力响应规律做了很多的研究工作。
目前,由于大型边坡振动台试验的成本及试验周期等问题,所得到的有效试验数据相对较少,使得对于强震作用下岩质边坡地震动响应及其震裂松动演化特征的认识还较为缺乏。因此,本文开展的大型均质岩质边坡振动台试验研究不仅可以深化对于强震触发边坡失稳机理这一科学难题的认识水平,而且也将促进边坡抗震防护技术的提升,指导防灾减灾工作。
1 试验仪器及设备
本试验在中国水利水电科学研究院工程抗震中心开展,使用的是德国INSTRON 公司生产的大型三向六自由度模拟地震振动台,台面空载情况如图1所示。使用的振动台的台面尺寸为5 m×5 m,最大载重量为20 T,其工作频段为0.1~120 Hz,可以实现三向六自由度各种地震波、随机波振动加载,满载作用下水平向最大加速度为1.0 g、竖向最大加速度为0.7 g,空载下最大水平向加速度为1.8 g、竖向加速度为1.3 g,最大倾覆力矩为35 t·m。试验过程中可以进行多道数据同时采集储存,可以通过增加数据采集仪的形式增加采集通道,数据采集系统如图2 所示。

图1 大型三向六自由度振动台Fig. 1 Large scale shaking table

图2 多道数据采集系统Fig. 2 Multi-channel data acquisition system
在岩质边坡振动过程中研究的主要测量参数包括加速度、速度和位移,其中最常用到的是加速度,因此在综合考虑试验成本、方便操作等因素,本试验采用的是加速度传感器。量程为±5 g,灵敏度1000 mv·g-1,频率范围( ±10%) 0.1 ~1000 Hz,谐振频率5 kHz,分辨率0.000 02 g。
2 相似材料配制及边坡模型砌筑
本文采用了铁粉、重晶石粉、石英砂、石膏、水作为相似材料配置均质岩质边坡,配置成的材料物理力学参数如表1 所示。均质边坡物理模型是在实验室的模型框架内砌制而成,然后对将材料加入搅拌桶并且加入适量的水充分搅拌均匀,之后从搅拌桶铲出堆至模型框内,分层铺开,尽量每铺设5 cm厚度便开始用振捣泵振捣均匀,以防止模型内部因不均匀流动产生空洞。在材料分层砌筑过程中,按照设计的图纸( 图3) ,在对应点处分层埋置传感器,砌筑成型的模型如图4 所示。

表1 边坡模型相似材料物理力学参数Table 1 Physical and mechanical parameters of the slope model similar material

图3 均质岩质边坡概化模型及传感器布置图( 单位:cm)Fig. 3 Generalized model of homogeneous rock slope and layout of sensors( unit: cm)
边坡模型几何尺寸为长3.5 m×宽0.68 m×高1.2 m,坡角为45°。在坡体内部如图3 所示布置21个传感器,其中有1 个传感器布置在台面以对输入波形进行校核,共使用22 个加速度传感器。
在边坡模型前后与模型框架钢板之间各充填4.5 cm 的阻尼液( 硅胶) ,以降低刚性模型框架对边坡模型的边界效应,有关模型边界效应的研究董金玉( 2010) 、杨国香( 2011) 、刘汉香等( 2014) 、范刚( 2016) 等人的博士论文中也都做了相关的研究。这些学者对于模型与框架的前后部位都是使用泡沫作为缓冲材料,以降低这种边界效应,但是由于泡沫在模型与框架之间只有受到挤压作用时才发挥效用,在模型与框架之间发生相向运动时就没有作用。而本文的试验过程中在前后边界处采用的是阻尼液作为缓冲材料,该材料能够在模型与框架之间发生拉压作用时均黏接在两者之间发生流动变形。

图4 模型砌筑完成Fig. 4 Finished the model masonry
3 均质边坡振动台试验结果及分析
在分析讨论输入应力波的频率以及幅值对均质边坡动力响应的影响时,主要从沿坡表水平距离方向监测点a20、a21、a22、a2、a3、a4、a18、a19( 共8个) ,向坡内水平距离方向监测点a20、a10、a9、a8、a7、a6( 共6 个) ,向坡顶垂直距离方向监测点a8、a12、a15、a4( 共4 个) 这3 个方面分别分析研究了水平、竖直方向加速度放大系数的规律,3 条研究剖线如图5 所示。本文中定义: 以坡脚处监测点a22 为基准,其他各测点相对于该基准点处加速度最大值的比为加速度放大系数。
3.1 不同频率波形输入对均质岩质边坡动力响应影响分析
3.1.1 沿坡表水平距离加速度放大规律
以加速度幅值为0.3 g 水平单向正弦S 波加载条件下为例,由 图6 可知,由低频到高频( 15 ~75 Hz) 情况下,沿坡表( 图5) 水平距离方向上观测点在水平向和竖向的加速度放大系数结果。

图6 沿坡表水平距离方向观测点的加速度放大系数( 幅值0.3 g)Fig. 6 Acceleration amplification coefficient along the slope surface( when acceleration amplitude is 0.3 g)
通过白噪声扫描测得均质岩质边坡模型的自振频率为61.77 Hz,由图6 结果可以看出,在频率较低时( 15 Hz、30 Hz) ,水平加速度放大系数沿坡表水平距离方向上是单调增大的,坡肩处水平加速度放大系数达到最大值,这一现象与杨国香( 2011) 的试验结论基本吻合; 当频率继续增加靠近模型的自振频率附近时,沿坡面水平加速度放大系数不再单调增大,而是不断减小,到达坡肩处时略微增大; 当频率增加至75 Hz 时边坡模型不再呈现出放大现象,说明高频振动下边坡模型的动力放大特性基本消失。
竖向加速度放大系数的最大值出现在坡脚之上坡面的中下部,随后一直减小,到模型后缘处有一个翘起现象,并且放大系数并不都大于1,而是与频率有关,这一结论与杨国香( 2011) 的试验现象并不相同; 同时,模型的前缘监测点放大系数较相邻点增大,这种现象的产生推测是由于模型框架的边界效应引起的; 当频率和幅值都较低时,放大现象比较明显; 同样的幅值下,低频所引起的竖向加速度放大效应更为显著,而频率增大时放大效应明显降低;当频率增加至75 Hz 时边坡模型不再呈现出放大现象,说明高频振动下边坡模型的动力放大特性基本消失。
整体来看,竖向加速度放大系数较水平向加速度放大系数更大。
3.1.2 水平坡内方向加速度放大规律
图7 给出了加速度幅值为0.3 g 水平单向正弦S 波加载条件下,由低频到高频( 15~75 Hz) 情况下,沿Z=0( 图5) 水平坡内方向上观测点在水平向和竖向的加速度放大系数结果。如图5 中所示,试验过程中在Z=30 cm、60 cm 的竖直剖面上也布置了若干传感器,但是由于编号为a13、a17 的加速度传感器埋置在坡体内部出现受潮接触不良,导致采集到的数据误差较大,故这里仅分析Z=0 剖面处的监测点数据。

图7 向坡内Z=0 处水平距离观测点的加速度放大系数( 幅值0.3 g)Fig. 7 Acceleration amplification coefficient along the profile at Z=0( when acceleration amplitude is 0.3 g)
由图7 结果分析可知,在Z=0 的水平面上,往坡内方向水平加速度没有明显变化,反而是随着频率的增加而出现减小的趋势,这与前人关于均质边坡的研究结论也较为接近,由于本次试验边坡模型比前人关于均质边坡模型要大,水平方向上监测点更多,所以所得到的结果和趋势进一步的完善了前人的研究成果( 杨国香,2011) 。而竖向加速度往坡内方向,出现先增大随后持续减小的趋势; 当到达坡体后缘处出现突然增大的现象,推断导致这一现象的原因都是边界处的刚性框架引起的。
3.1.3 向坡顶方向加速度放大规律
如图8 给出了加速度幅值分别为0.3 g 水平单向正弦S 波加载条件下,由低频到高频( 15 ~75 Hz)情况下,沿X=90 cm( 图5) 向坡顶方向上观测点在水平向和竖向的加速度放大系数结果。如图5 中所示,试验过程中在X=112 cm、172 cm 的竖直剖面上也布置了若干传感器,但是由于编号为a13、a17的加速度传感器埋置在坡体内部出现受潮接触不良,导致采集到的数据误差较大,故这里只分析X=90 cm 剖面处的监测点数据。
由图8 结果分析可知,在X=90 cm 的竖直面上,当频率≥45 Hz 较高时,水平向加速度放大系数基本都小于1; 而当频率为15 Hz、30 Hz 较低时,随着高程的增大,表现出了非线性增大效应; 且较高频时表现显著,整体的变化趋势是边坡上部要明显于下部。此外,对于竖向加速度放大系数,随着高程的增加表现出了一定的波动性。
3.2 不同幅值波形输入对均质岩质边坡动力响应影响分析
3.2.1 沿坡表水平距离加速度放大规律
如图9 给出了加速度频率为15 Hz 水平单向正弦S 波加载条件下,由低幅值到高幅值( 0.1 ~0.4 g) 情况下,沿坡表( 图5) 水平距离方向上观测点在水平向和竖向的加速度放大系数结果。
由图9 结果分析可知,低幅值情况下的水平加速度放大系数更明显; 并且基本都是沿坡面水平加速度放大系数呈现非线性放大的规律,到达坡肩处达到最大值; 但是当加速度幅值为0.1 g 时,最大值出现在坡肩之下,随后各种幅值下水平加速度放大系数都是逐渐减小。
沿坡表观测点的竖直加速度放大系数在低幅值下的放大效应强于高幅值,也都是在坡角之上坡体中下部出现最大值,然后一直单调减小。并且,沿坡表竖直加速度放大系数要明显大于水平加速度放大系数。

图8 向坡顶X=90 cm 处垂直方向观测点的加速度放大系数( 幅值0.3 g)Fig. 8 Acceleration amplification coefficient along the profile at X=90 cm( when acceleration amplitude is 0.3 g)
3.2.2 水平坡内方向加速度放大规律
如图10 给出了加速度频率分别为15 Hz 水平单向正弦S 波加载条件下,由低幅值到高幅值( 0.1 ~0.4 g) 情况下,沿Z=0( 图5) 水平坡内方向上观测点在水平向和竖向的加速度放大系数结果。
由图10 结果分析可知,低频情况下的水平加速度放大系数受幅值的影响较小,在15 Hz 时基本不受幅值影响; 随着频率的增大,远离坡面放大系数有减小的趋势,但是并不十分明显。
而竖向加速度放大系数远离坡面水平方向上,在频率较低时,呈现出了一定的波动效应; 随着频率的增加,低幅值加载下的放大系数要大于高幅值;并且基本都是远离坡面先增大,然后减小的趋势。
3.2.3 向坡顶方向加速度放大规律
如图11 给出了加速度频率分别为15 Hz 水平单向正弦S 波加载条件下,由低幅值到高幅值( 0.1~0.4 g) 情况下,沿X=90 cm 向坡顶方向上观测点在水平向和竖向的加速度放大系数结果。
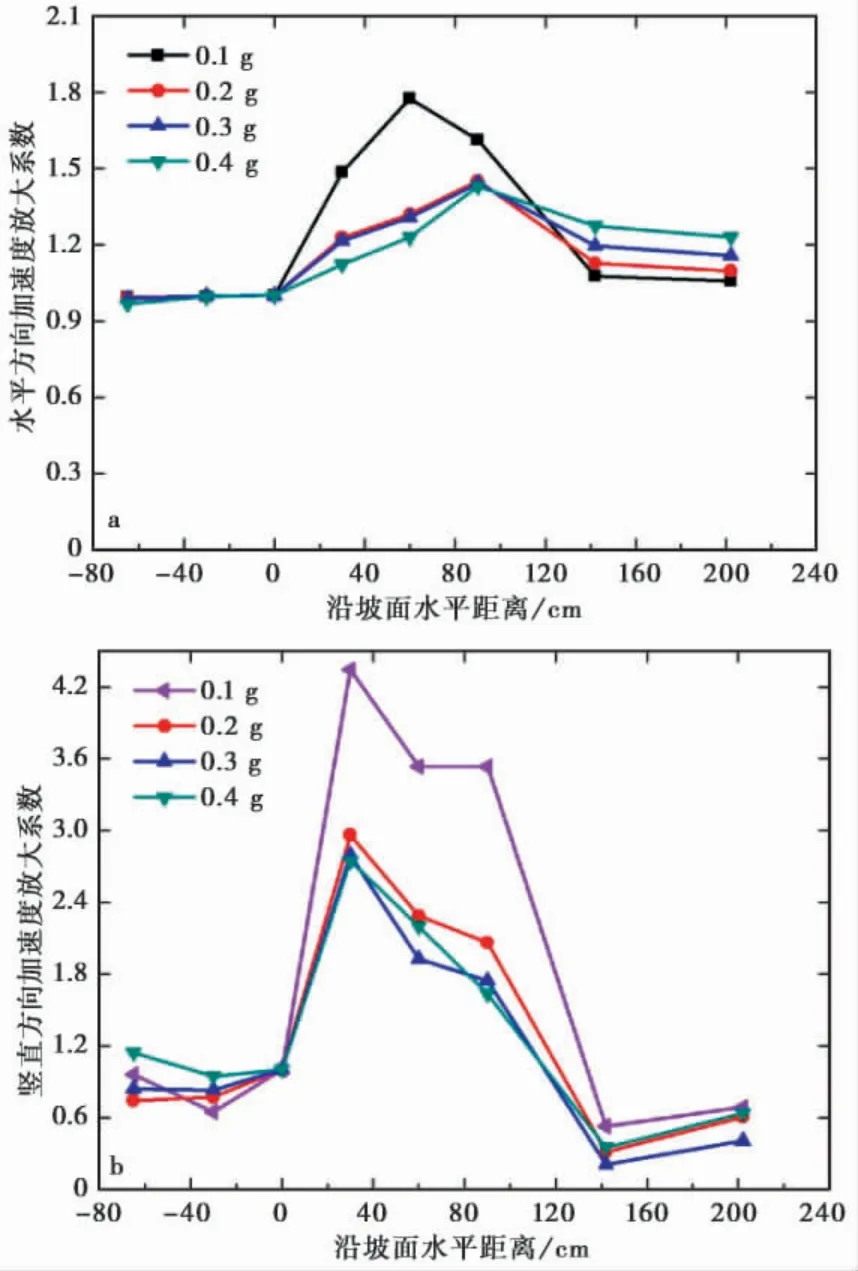
图9 沿坡表水平距离方向观测点的加速度放大系数( 频率15 Hz)Fig. 9 Acceleration amplification coefficient along the slope surface( when acceleration frequency is 15 Hz)
由图11 结果分析可知,在X=90 cm 的竖直面上,在频率较低时,水平加速度放大系数随着幅值的变化并不明显; 当频率增大时,低幅值加载下的水平加速度放大系数要大于高幅值条件; 并且,随着高程增加,水平加速度放大系数逐渐增大,但是都小于1; 当频率达到75 Hz 时,边坡模型的动力响应无明显规律。
在X=90 cm 的竖直面上,竖向加速度放大系数在低幅值下的要大于高幅值的情况,并且随着高程的增加低幅值下的放大系数增大的更为明显; 整体的趋势是先减小后增大,当到达坡体上部时放大更为明显。
3.3 均质岩质边坡动力加载过程中自振频率变化

图10 向坡内Z=0 水平距离方向观测点的加速度放大系数( 频率15 Hz)Fig. 10 Acceleration amplification coefficient along the profile at Z=0( when acceleration frequency is 15 Hz)
在均质岩质边坡振动台试验过程中,每次波形加载完成之后都进行了白噪声扫描,以测得边坡模型的自振频率变化。由于均质边坡在振动加载过程中没有出现明显大变形,相同幅值不同频率时的自振频率变化不明显,如图12 给出了加载频率为30 Hz 时不同幅值下的模型自振频率。其中,模型的起始自振频率为61.77 Hz,0.1 g 加载后自振频率为60.06 Hz,0.2 g 加载后自振频率为59.57 Hz,0.3 g 加载后自振频率为57.86 Hz,0.4 g 加载后自振频率也是57.86 Hz,0.5 g 加载后自振频率也是56.15 Hz。
从图12 可以看出,由于模型与框架之间存在黏结作用,经过起始0.1 g 振动之后自振频率有明显降低; 随着幅值进一步增大,从0.2 ~0.3 g 频率进一步降低,到达0.4 g 之间保持不变; 当幅值增大至0.5 g 时,再次急剧降低,说明模型随着振动的加强而逐渐发生变形。通过自振频率随着幅值以及加速度的变化规律,可以较好的说明前人对于均质边坡动力响应规律的振动台试验研究并非是一成不变的,也需要充分考虑加载频率以及加载幅值的影响。
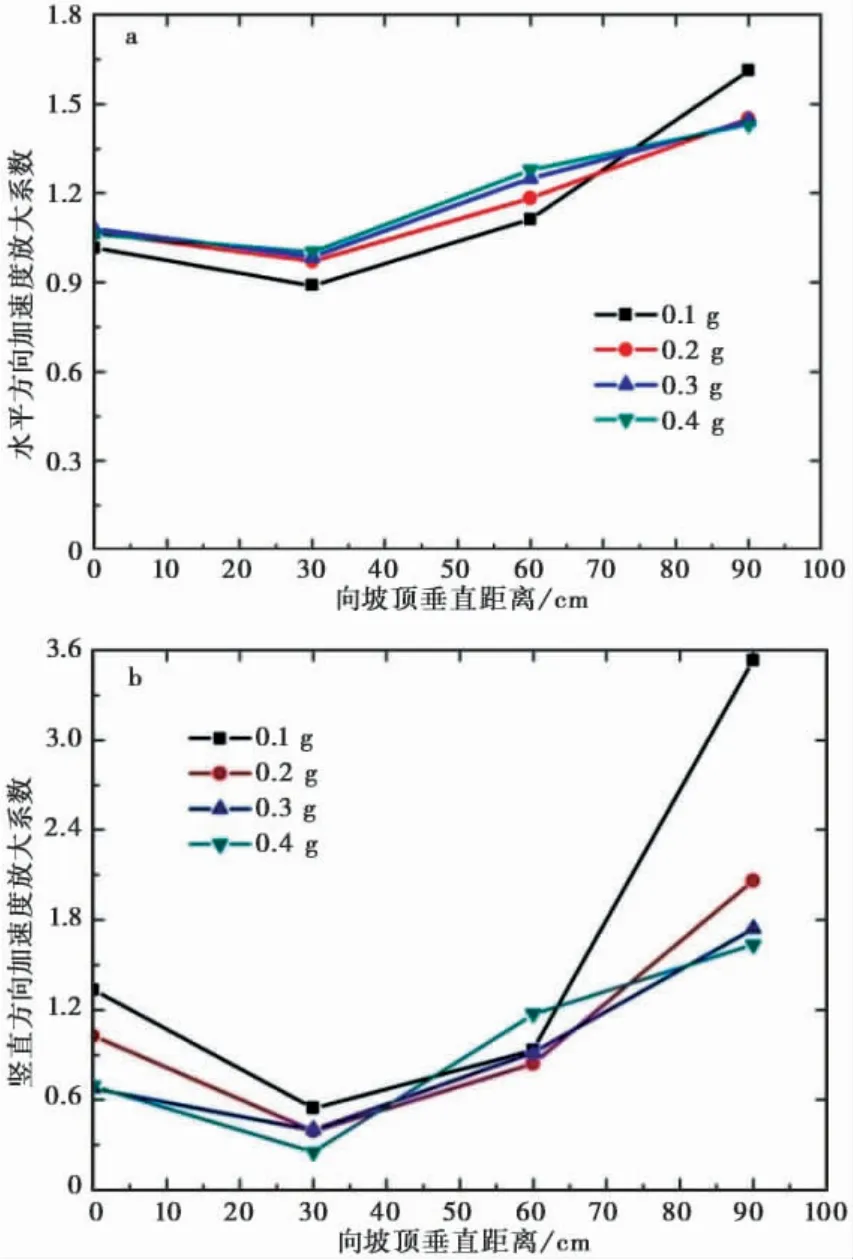
图11 向坡顶X=90 cm 处垂直方向观测点的加速度放大系数( 频率15 Hz)Fig. 11 Acceleration amplification coefficient along the profile at X=90 cm( when acceleration frequency is 15 Hz)

图12 不同幅值加载下均质边坡模型自振频率变化Fig. 12 Natural frequency variation of homogeneous rock slope under different acceleration amplitude loading
4 讨论与结论
本文开展了大型均质岩质边坡振动台试验,采用铁粉、重晶石粉、石英砂、石膏、水作为相似材料,采用在边坡模型前后边界采用阻尼液的处理措施,对边坡模型的建造细节建立了一套可行性很高的工艺方法,并详细分析了均质岩质边坡地震动响应特征,得到如下主要试验结论:
( 1) 当频率较低时,沿坡表水平距离方向上监测点的水平加速度放大系数是单调增大的,坡肩处水平加速度放大系数达到最大值; 当频率继续增加靠近模型的自振频率附近时,沿坡面水平加速度放大系数不再单调增大,而是不断减小,到达坡肩处时略微增大,当频率增加至75 Hz 时边坡模型不再呈现出放大现象。
(2) 沿坡表水平距离方向上监测点的竖向加速度放大系数的最大值出现在坡脚之上坡面的中下部,随后一直减小,到模型后缘处突然增大,并且放大系数并不都大于1,而是与频率有关,这一现象与前人的研究结论不同; 同时,模型的前缘监测点放大系数较相邻点增大,这种现象的产生可能是由于模型框架的边界效应引起的,在前人的研究中受限于模型尺寸和观测点较少,这一现象也是首次观察到; 当频率和幅值都较低时,放大显现比较明显;同样的幅值下,低频所引起的竖向加速度放大效应更为显著,而频率增大时放大效应明显降低。当频率增加至75 Hz 时边坡模型不再呈现出放大现象,说明在接近或超过模型的自振频率的高频振动下,均质边坡模型的动力放大特性基本消失。
( 3) 在Z=0 的水平面上,往坡内方向水平加速度没有明显变化,反而是随着频率的增加而出现减小的趋势,由于本次试验边坡模型比前人关于均质边坡模型要大,水平方向上监测点更多,所以所得到的结果和趋势进一步的完善了前人的研究成果。而竖向加速度往坡内方向,具有一定的波动特性。
( 4) 在X=90 cm 的竖直面上,高频加载时,水平向加速度放大系数基本都小于1; 而频率为15 Hz、30 Hz 较低时,随着高程的增大,表现出了非线性增大效应,整体的变化趋势是边坡上部要明显于下部。此外,竖向加速度放大系数在低幅值下的要大于高幅值的情况,并且随着高程的增加低幅值下的放大系数增大的更为明显; 整体的趋势是先减小后增大,当到达坡体上部时放大更为明显,表现出了一定的波动性。
( 5) 相同幅值下不同频率加载条件下,均质边坡模型的自振频率变化整体来看不太明显,而输入加速度幅值的变化对自振频率的改变更为显著。此外,可以看出低频成分对模型损伤不明显,高频及自振频率附近频段对均质边坡的损伤更为强烈,导致模型的自振频率下降。本研究为今后此类岩质边坡地震动响应研究提供了参考。

