联合Laplacian正则项和特征自适应的数据聚类算法∗
郑建炜 , 李卓蓉,2 , 王万良 , 陈婉君
1(浙江工业大学 计算机科学与技术学院,浙江 杭州 310023)
2(浙江大学城市学院 计算机与计算科学学院,浙江 杭州 310015)
聚类分析是数据挖掘领域的研究热点之一,旨在无标签情形下对数据进行分组,使组内数据尽可能相似而组间数据尽可能不同,被广泛应用于图像分割[1]、目标分簇[2]、深度学习模型[3]等科学应用领域.在大数据背景下,实际输入数据除“海量样本”特点外,还具有极高的特征维数.以在线文本数据为例,当采用矢量空间描述每个文档时,大词汇量往往导致样本维数达到5 000以上.此外,一张解析度为256×256的图像矢量化后的维数则是65 536.受“维数灾难”限制,对高维数据进行合理高效的聚类分析是一个极具挑战性的问题.过高的样本维度包含冗余的特征信息和异常噪声,不仅降低了后续聚类操作的运算效率,也影响了其他性能指标.针对该问题,常见的思路是引入特征选择进行维数预约简,然后在子空间进行相似度矩阵构建并对嵌入数据实施谱聚类分析.
特征选择(feature selection,简称FS)[4]从原始样本空间中挑选最具代表性的维数子集,其核心问题依据特定准则评价各子集的优劣并确定选择结果.传统搜索策略[5]的缺点是直接利用数据的统计指标对每个特征进行单独评分并取分值较高者为结果集,缺乏整体的优劣评判标准[6].针对此问题,学者们开展了联合特征选择研究,通过稀疏正则化约束[7]进行特征选择并兼顾子空间学习.Cai等人[8]结合流形学习和l1正则化模型进行稀疏的联合特征选择.所选用的l1范数虽然意义明确,但其稀疏性仅作用于独立的特征点[9].更多的算法[10]通过对投影矩阵约束l2,1范数以保证行稀疏,选择矩阵非零行对应的特征集合为最优特征子集.在评价准则方面,通常选择能有效保持数据本质结构的特征,采用图论模型刻画全局结构、局部流形以及鉴别性信息等.多簇特征选择法(multi-clusters FS,简称MCFS)[8]首先计算高维数据的低维流形嵌入,然后对投影矩阵采用l1范数进行稀疏约束,根据回归系数对每个特征进行排序,最终选择最易保持局部流形结构的特征.局部学习聚类(local learning based clustering for FS,简称LLCFS)[11]将特征关联性引至内置的正则化局部学习模型,使得演化的Laplacian图能够迭代优化.自适应结构学习(FS with adaptive structure learning,简称FSASL)[12]旨在结合全局信息挖掘以及局部流形学习进行样本结构保持,兼顾了稀疏性和保局性两种优势.局部保持得分法(locality preserving score,简称LPS)[13]则从误差抑制的角度出发,对每个特征的重构能力进行排序,获得最优的子特征集.上述算法采用独立的步骤按序进行子空间学习和聚类操作,其弊端是无法达到聚类目标的整体最优效果.常见的解决方案是将子空间聚类融合为联合优化整体,通过聚类指标和降维指标互相反馈优化模型的各约束项.鉴别嵌入聚类法(discriminative embedded clustering,简称DEC)[14]联合Fisher鉴别投影和k-means提出一致性的分簇框架,但其受限于k-means的本质约束,无法适应单流形多环分布数据.非负鉴别法(nonnegative discriminative FS,简称NDFS)[15]将聚类标签反馈于特征选择步骤,提升了特征子集的鉴别性,然而其特征选择过程缺乏结构性意义,且算法容易陷入局部最优点.
提升相似度矩阵(或称为关联矩阵、邻接矩阵)结构是进一步改进子空间聚类性能的关键思想,也是谱聚类算法的核心步骤.Wang等人[16]基于局部线性嵌入思想[17]构建Laplacian图,获得了良好的标签传播性能.Elhamifar等人[18]则以全局线性表示系数作为关联矩阵构建基础,通过l1范数提出了稀疏子空间聚类法(sparse subspace clustering,简称SSC).SSC假设每个数据由同一子空间中其他样本稀疏表示,挖掘不同组的表示关系,但其缺乏空间分布结构考虑.Liu等人[19]提出了低秩表示(low-rank representation,简称LRR)聚类法,利用核范数约束系数矩阵,获得更好的全局性.SSC和LRR以输入样本子空间相互独立或正交为假设,其理想状态下的相似矩阵具有刻画子空间属性的块对角结构.进一步,Lu等人[20]给出了一组强制块对角条件,并指出:在数据充分并且子空间相互独立的前提下,正则项满足该条件可保证相似矩阵具有块对角结构.Feng等人[21]将对应的拉普拉斯矩阵进行低秩约束,并添加至SSC和LRR以保证块对角状态,获得更优的相似度结构.此外,在系数矩阵优化问题上,新晋算法都采用Laplacian正则项约束提升相似度矩阵的块对角结构[22−24],非负稀疏Laplacian正则约束的LRR模型(non-negative sparse Laplacian regularized LRR,简称NSLLRR)[22]以非负性、稀疏性为条件,增加超图拉普拉斯约束,具有良好的样本表示能力.Hu等人[23]提出的光滑表示聚类模型(smooth representation clustering,简称SMR)基于增强型组效应条件进行相似性度量,算法在保证高质量聚类性能的前提下获得了大幅度效率提升.为更好地逼近低秩结构,分组低秩结构模型(low-rank structure,简称LRS)[24]引入组指示规化对各簇样本进行Schattenp范数正则项约束,其缺陷是抗噪性差且模型运算效率较低.
综上所述,现存的特征选择型算法缺乏样本间关联结构描述,导致次优的聚类性能;而Laplacian正则型表示模型则都采用原始数据直接构建关联矩阵,独立于表示系数更新操作,也不具备整体算法的最优性.虽然鲁棒子空间分割法(robust subspace segmentation,简称RSS)[25]实现了重构系数和相似度矩阵的兼顾学习,具有更优的结构挖掘能力,但缺乏特征优选机制,对现实高维数据的抗噪性弱,且其自表示框架受稀疏性、非负性等约束的影响,运行效率较低,样本规模尺度化能力有待进一步提高.针对现存算法的问题,本文基于自适应近邻进行图拉普拉斯学习,将低维嵌入、特征选择和簇结构学习纳入同一框架,提出一种兼顾自适应特征优选和簇结构学习的聚类模型,即联合拉普拉斯正则项和自适应特征学习(joint Laplacian regularization and adaptive feature learning,简称LRAFL)的数据聚类算法,具体工作如下.
1) 提出一种图Laplacian矩阵更新策略,保证其秩结构与目标聚类数的一致性,使得模型优化结果直接具备分簇块对角结构,规避了后续k-means、谱分解等操作;
2) 将特征学习机制融入Laplacian矩阵构建框架,在保证噪声特征抑制的前提下,去除高复杂度的表示系数学习过程,提升模型求解效率;
3) 设计具备唯一最优解的参数优化方案,对模型部分待定参数进行推演分析,给出更具指示意义的设定方法,进一步加速模型实现效率.
1 相关工作
本节介绍谱聚类算法中的两个关键步骤,即相似度矩阵构建和拉普拉斯正则约束项,其中,前者用于挖掘数据分布结构,而后者是引导块对角状态的核心技术.
1.1 相似度矩阵构建
传统的相似图构建方法如ε邻域图、k近邻图、全连接图等都存在着明显的缺陷,包括:(1) 分析尺度选择困难;(2) 参数敏感性强;(3) 多尺度数据适应度弱;(4) 抗噪性差等等.为解决存在的问题,Wang等人[16]在邻域图基础上通过线性表示计算相似度权值,提升了算法抗噪性;Zelnik-Manor等人[26]提出自校正谱分簇算法,缓解了第1个和第3个缺陷.Cheng等人[27]引入稀疏表示进行邻域图构建,可以有效解决第1个和第4个问题,也规避了高敏感性的待定参数ε和k,但其正则项参数的敏感性仍然较强,且存在l1范数求解运行效率低的问题.Huang等人[28]采用非负和加权限制替代文献[27]中的l1范数约束,提出了单纯型稀疏表示(simplex sparse representation,简称SSR)邻域图构建方法,能有效解决上述前3个问题;而且算法不需要人工设定参数,运行效率和实现简易度亦优于其他对比算法.
给定数据集X=[x1,x2,…,xn]∈Rm×n,其中,xi是第i个m维输入样本,n是训练样本总数.定义邻域图模型S,其元素sij表示数据点xi与xj互为近邻的概率,si∈Rn表示S的第i个列向量.SSR的目标函数为

其中,X−i=[x1,…,xi−1,0,xi+1,…,xn]表示剔除第i个输入数据的训练样本集,0是m×1的零向量,1是元素全为1的n×1向量.公式(1)通过重构表示能力说明高权值系数的成对样本具有更高的概率互为近邻,具有天然的样本稀疏性和奇异点抗噪性,其缺点是不具备特征稀疏性,因此不适于高维度冗余数据应用.
1.2 Laplacian正则约束
Laplacian矩阵构建的方式多样,且各算法的作者都称自己的谱分析矩阵为Laplacian.给定对称的相似度矩阵S,RatioCut[29]所构建的Laplacian矩阵为L=D−S,其中,对角矩阵D称为度矩阵,相应的对角元素NCut[30]将上述L进行规范化操作,即Ls=D−1/2LD−1/2或Lns=D−1L,其中,前者是对称矩阵而后者是非对称矩阵.当给定非对称的S时,则相应的非规范化Laplacian矩阵计算为L=D−(ST+S)/2[13,31],其中,度矩阵D的对角元素为在经典谱聚类算法中,无论Laplacian矩阵形式如何,后续操作都对该矩阵进行特征求解,并针对前c个特征矢量进行k-means聚类,其中,c是数据簇结构目标.
最近,Hu等人[23]以谱聚类为基础,结合低秩重构表示思想将一般的表示型谱聚类模型归纳为

其中,α>0是平衡参数,A(X)表示字典矩阵,Z是系数矩阵,||⋅||l表示合适的范数.公式(2)前半部分刻画了重构表示A(X)Z逼近数据X的程度,后半部分是Laplacian谱约束正则项.
稀疏子空间聚类对公式(2)的正则项采用某种稀疏度量,从而使Z具有特定目标结构.常见的包括SSC的l1范数约束、LRR的核范数约束以及SMR和RSS的组效应约束等等.考虑到块对角结构的相似矩阵能更好地刻画簇结构属性,Feng等人[25]利用相似度矩阵对角块个数与Laplacian矩阵秩约束之间的关系,对图拉普拉斯矩阵添加秩约束:
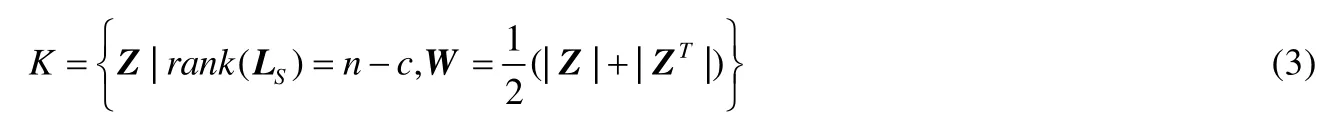
其中,c表示对角块的个数,也即簇目标数.将上述秩约束添加至子空间聚类模型,可保证清晰的块对角结构,具体目标模型描述为

其中,λ是平衡参数;diag(Z)=0用于约束对角元素zii=0,以避免平凡解.
2 LRAFL算法描述
结合现有工作,考虑到自适应邻域学习和块对角Laplacian矩阵对聚类效果的重要性以及自表示学习的复杂性,本节将公式(1)和公式(4)中的表示系数转变为邻域结构约束,并辅以稀疏性、参数自学习、特征寻优以及簇结构直接确定等优势,提出一种兼顾特征选择和谱聚类的算法LRAFL.首先对该算法目标函数的构建过程进行描述,然后给出了模型求解优化方案.
2.1 目标函数构建
探索数据的局部连通性,即相似度权值,是聚类任务的典型策略[32].根据本文开始部分的描述,常规的表示系数[18,19]和线性关联[16]都存在计算效率低以及缺乏全局最优等弊端,本节直接以相似度计算为基础,辅以特征加权、低秩块对角约束等构建目标函数.首先给定任意输入数据xi和xj,其距离与相似度权值sij应呈反比关系,即短距离对应大权值、长距离对应小权值.因此,结合公式(1)对权值的概率条件约束,一种自然的相似度计算方法为

然而,公式(5)具有平凡解,仅xi的最近邻样本获得概率相似度1而余下的sij=0.另一方面,如果在不包含任何距离信息约束下求解式:

则得到另一种平凡解,即所有样本都是xi的近邻且概率相似度为1/n,可以看作相似度赋值的先验分布,其本质则是l2范数约束条件[33].结合公式(5)和公式(6),xi的邻域相似度计算为

其中,第2项为正则项,β是正则化参数.联合所有的输入数据xi,i=1,…,n,则完整的相似度计算可以描述为
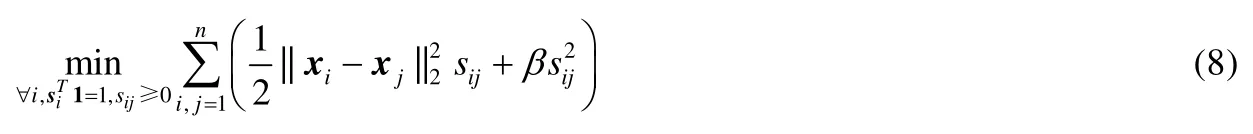
通过第2.2节模型优化求解过程可知,公式(8)中各相似度矢量si具有稀疏的闭式解,模型优化效率高且能够有效抑制奇异噪声样本.
其次,为引入特征优选机制,使算法具有奇异特征抑制性能,采用特征加权因子w∈Rm×1将公式(8)调整为

其中,⊙表示元素相乘符号.与公式(5)和公式(6)类似,直接以公式(9)为目标函数会出现平凡解.即:当w取零向量且相似度为1/n时,模型值最小.因此,进一步将相似度约束条件添加至w权值矢量,即:
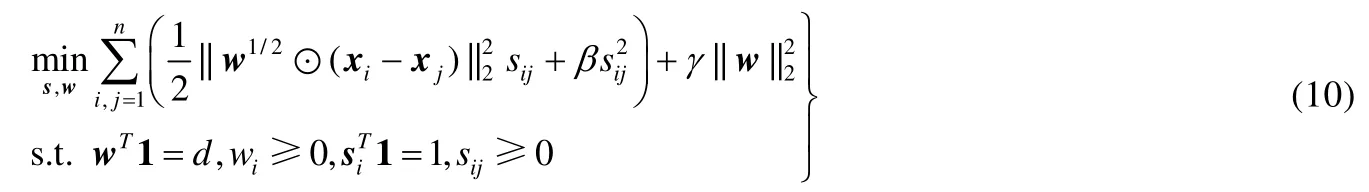
其中,d≤m表示选择后有效特征数.公式(10)第1部分用于相似度矩阵构建,子项在特征优选约束下,使邻近的样本对具有更高的相似度权值,而非近邻样本对具有较低的相似度权值,余下部分是特征加权矢量和相似度值的l2范数约束,用于规避平凡解并引导模型未知量具有光滑的数值结构.
文献[14]等聚类算法通过投影矩阵进行特征提取,相比较而言,公式(10)采用特征选择操作拥有的优势包括:(1) 所采用的矢量操作较特征提取算法的特征分解操作效率更高;(2) 对于输入数据不同特征的支撑作用具有更加明确的物理意义;(3) 可以在不指定特征子集规模的前提下进行加权赋值,而特征提取必须指定子空间维数.此外,通过对公式(10)模型中相似矩阵S和特征权值矢量w进行交替优化,可同时实现流形结构学习和联合特征选择.通过S的迭代更新和优化,使得近邻关系具有自适应性,从而确保特征选择及谱聚类不再基于固定不变的图Laplacian结构.
与其他谱聚类算法相似,公式(10)得到的相似矩阵S不能直接用于数据聚类,需进行谱分析且利用k-means得到聚类结果[32].根据定理1可知:当Laplacian矩阵Ls的秩为n−c时,则相应的相似矩阵S恰好具有c分簇对角结构,无需额外的k-means操作.为实现该目标,将文献[20]中的低秩约束(即公式(3))引入公式(10),则有:

其中,rank(Ls)=n−c约束项与定理1中的零特征值重根数等价.然而,直接对公式(11)求解非常困难[21],本文根据命题1进一步将公式(11)调整为
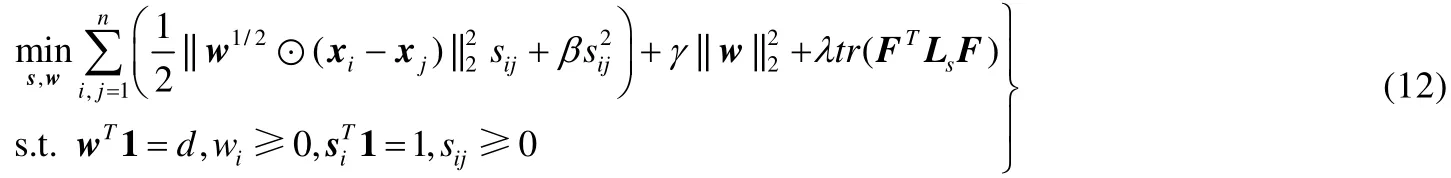
其中,符号tr是矩阵的迹,F∈Rn×c是Laplacian矩阵Ls相应c个最小特征值的特征矢量.公式(12)是最后的LRAFL模型目标函数,基于自适应邻域学习构建图Laplacian矩阵,将低维嵌入、特征选择和谱聚类纳入同一框架,并添加非负加和约束以及等价低秩约束,模型结果具有明确的块对角结构.
定理1[21,32].相似矩阵S对应的拉普拉斯矩阵Ls中,特征值为0的重根数与相似矩阵S中块结构的数量相等.
命题1.最小化Tr(FTLsF)与rank(Ls)=n−c具有等价性,其中,F∈Rn×c.
证明:假设σi(Ls)是Laplacian矩阵第i小的特征值,根据拉普拉斯矩阵的半正定性[32],σi(Ls)≥0成立,因此对Ls秩约束为n−c等同于约束.再根据Ky Fan定理[34],即:
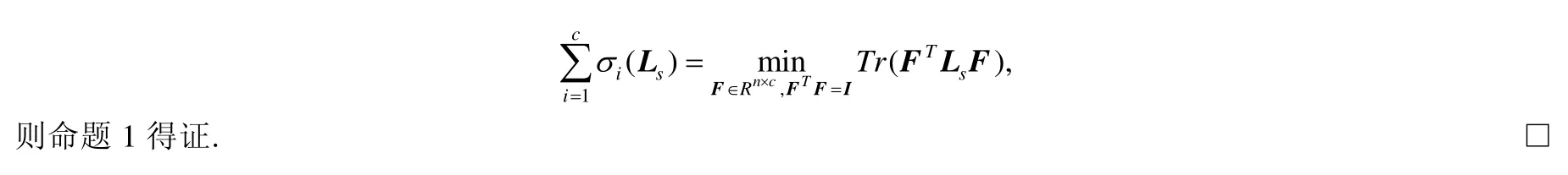
2.2 模型优化求解
在公式(12)中,相似矩阵S和特征权值向量w相互耦合,投影矩阵F的构建又依赖于相似矩阵和拉普拉斯矩阵,因此不能直接对其求取闭合解.本节采用交替优化的方法,依次对不同未知变量进行单变量优化,其中,每一次迭代都是一个凸优化过程.
首先,当固定相似矩阵S时,则F由Ls的前c个最小特征值所对应的特征向量构成,因此F也是固定矩阵.Ls是一个实对称半正定矩阵,通过奇异值分解可得到Ls=LLT.从而,目标函数(12)可以调整为
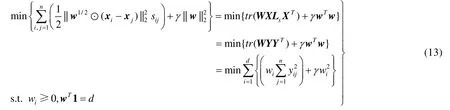
其中,W是以w为对角元素的对角矩阵,Y=XL,而yij是Y矩阵对应的元素.公式(13)是一个典型的二次规划问题,常见的数值最优化技术包括内映射牛顿法、有效集算法等[35]都能够对之进行迭代优化获得特征权值矢量w.为进一步提升效率,本文提出一种闭式求解方案,将公式(13)进一步调整为


综上所述,完整的LRAFL如算法1描述.值得注意的是:在公式(12)目标函数下,如忽略算法1的迭代框架,即先令sij=1,依公式(13)求解特征权值w;再固定w,联合优化S和F,可得到LRAFL模型的独立优化版(Ind),获得目标函数的快速解.然而该版本以模型次优性为代价,其实际应用性能弱于算法1.为有效平衡模型的实施性能和运行效率,通过设置收敛条件(见第3节描述),可使模型在Im<15次迭代内停止.
算法1.LRAFL描述.
输入:数据集X,聚类目标c,迭代总数Im,平衡参数γ,β,λ,有效特征数d;
输出:具有c分块对角结构的相似矩阵S,特征加权向量w.
1.初始化特征加权向量w0,设λ=0,通过公式(20)得到初始相似矩阵S0,并计算投影矩阵F0;
2.设迭代次数t=1;
3.固定相似矩阵和投影矩阵,依公式(15)计算特征加权向量wt,其中,Ls=D−S;
4.固定wt,根据公式(20)更新相似矩阵St并计算投影矩阵Ft;
5.如满足收敛条件或迭代t≥Im,则输出结果,算法中止;反之,令t=t+1,转至第3步.
3 LRAFL算法描述
通过算法1可见,LRAFL在实施过程中包含平衡参数γ,β,λ以及有效特征数d等待定参数,各类参数的优选过程不仅耗时而且对算法在不同数据集中的输出效果影响较大.因此,分析不同参数的具体实现推荐值是一个公知问题.此外,算法的收敛性和复杂度分析也对其具体的应用推广有着较大的影响.
3.1 参数设定细节
从公式(15)可见,特征加权向量w的取值由有效特征数d∈(0,m]和正则项平衡参数γ>0决定.具体实施过程中,可根据输入数据对其中一个参数进行指示推荐,减少算法的计算开销.首先,当输入纯净数据时,可以认为所有的特征都是有效的,不同维数依wi的取值具有不同的贡献度,即d=m.不失一般性,假设w1≥w2≥…≥wm≥0按照从大到小的顺序排列,依特征加权的非负性,令wm>0,则有:

将其中的γ代入公式(15),得到w的最终计算方法为

其中,仅存的人工设定参数d具有明确的物理意义,可依据输入数据按经验设定.
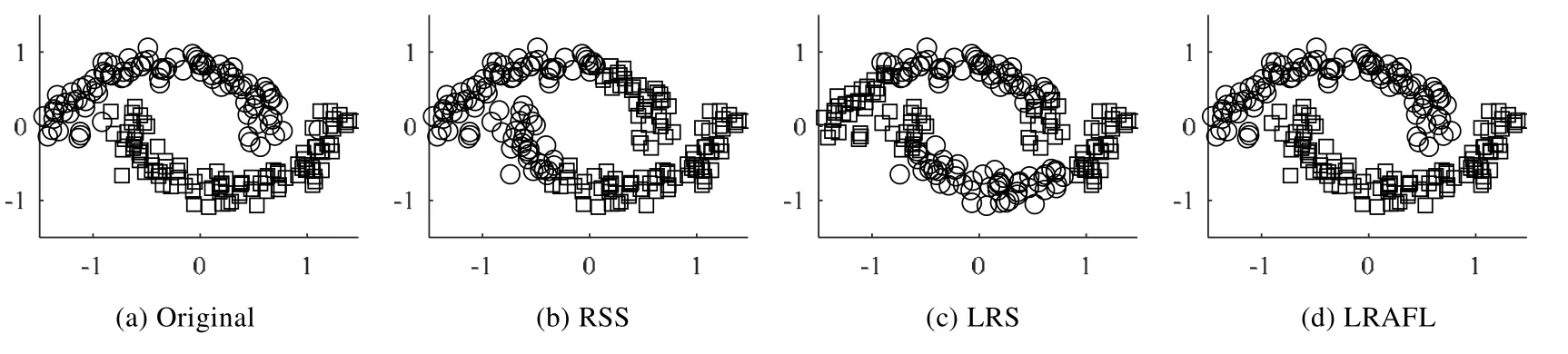
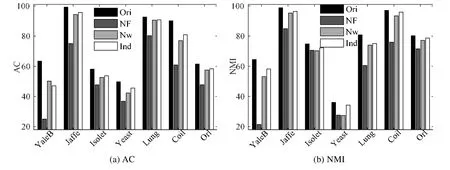
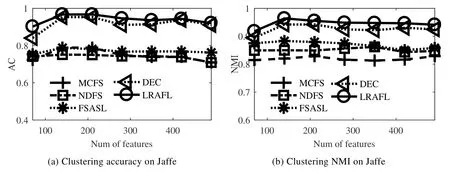
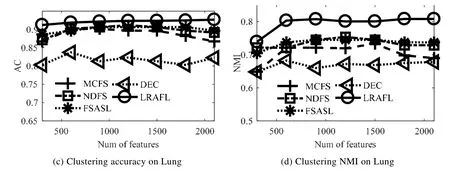
从公式(20)可见,相似矩阵中列向量si的取值由正则项参数βi>0决定.一般情况下,当得到的相似矩阵S全连通时,根据定理1可知数据为单簇结构,无法直接获得F∈Rn×c矩阵.此外,在实际应用中,数据局部邻域关系更能刻画本质结构,往往仅考虑数据点xi的k个邻域样本而非所有输入数据进行连接,而且稀疏的相似矩阵还能有效降低后续过程的计算量.因此,公式(20)中的n可由k替代且k< 由于k是正整数并且有明确的物理意义,因此公式(20)仅需调整k求相似度矩阵,比直接调整β更为便捷. 从命题1可知,Tr(FTLsF)与rank(Ls)=n−c等价,因此在目标函数的更新过程中,取足够大的λ参数值时,Tr(FTLsF)无限接近于0,可直接获得具有c分簇结构的相似矩阵S.因此,λ的取值可在算法运行中自适应确定,随机给定一个初始化值λ(如λ=β),每次迭代计算投影矩阵后,分别计算.给定接近于0的常数ε(本文选为1e−10),当ρ1>ε时,说明Tr(FTLsF)值不够接近于0,则增加λ值;反之,当ρ2<ε时,说明Tr(FTLsF)值过小,则减少λ值;当ρ1<ε<ρ2时,说明Ls矩阵恰好具有c块对角结构,模型收敛. 综上所述,虽然在算法1的描述中LRAFL有4个待设参数,但算法具体实施过程中仅d(或γ)值和k值需要作调整测试,而且各参数都有明确的意义和设置推荐,保证算法应用过程的快速实现. LRAFL采用交替更新法进行模型迭代求解,在固定部分变量的前提下优化余下未知变量.根据算法1的描述,每次迭代的关键步骤公式(15)和公式(20)都是闭式解,因此其单个变量更新是唯一解.命题2说明所提算法在迭代过程中使目标函数(12)的值逐步下降,并最终收敛. 命题2.算法1的目标函数值随迭代过程逐步下降. 证明:假设在迭代t时有相似矩阵St,则在t+1次迭代中,固定St并优化Ft+1和wt+1,以下不等式成立: 类似地,在固定Ft+1和wt+1时优化相似矩阵,则有不等式: 联合公式(28)和公式(29)可知,目标函数(12)的值随迭代过程逐步下降,命题2得证.□ 值得注意的是:为避免LRAFL算法进入局部收敛,可以尝试不同的初始化方案,例如w可以简单地初始化为元素值为1/d的列向量,亦可在非负加和约束下取随机值.此外,还可以在迭代循环外先初始化相似矩阵S,包括k近邻法或ε邻域法等,依不同输入数据集尝试不同的初始化方案,能使LRAFL有效逼近全局最优解. 算法1的关键耗时步骤是3个未知变量的更新操作,包括w,S和F.其中,w依公式(15)计算,其运算复杂度是O(d);S中的列向量依公式(20)计算,其运算复杂度是O(k),因此相似矩阵S的整体复杂度是O(k2);投影矩阵F通过Laplacian矩阵的特征分解获得,其复杂度是O(n3).一般情况下,d< 首先人工产生了5类独立的子空间,其环境维数为250,本质维数为4.对任意子空间,随机产生100个单位样本并将其中的50%叠加高斯噪声干扰,噪声等级为{0,0.3,0.6}.图1显示了几种具有相似性矩阵构建能力的聚类算法所生成的邻域图,包括LPS[13],RSS[25],LRS[24]和LRAFL. Fig.1 Affinity on synthesized data with different levels of noise corruption图1 五簇合成数据在不同噪声等级下的相似性结构 其中,图1(a)~图1(c)分别是无噪声干扰、30%噪声干扰和60%噪声干扰下的效果,所有算法的参数优选过程遵从第4.2节的描述.从图1可见:在第1行无噪声干扰环境下,4种算法都获得了高质量的相似度矩阵,为实现高性能的聚类结果奠定基础.然而,随着高斯噪声的引入,LRS的相似矩阵完全处于紊乱状态,无法体现5分簇结构.类似地,LPS的相似矩阵也趋于模糊,由5分簇结构逐渐退化为3分簇结构;RSS的关联矩阵在趋于模糊的基础上,不同组结构的相似度值亦呈现不平衡特性.对比可见:所提算法LRAFL具有更为清晰的5簇相似度矩阵,受噪声干扰的影响小于其他几种算法.值得注意的是:从图1(a.3)可见,LRS在干净环境下的相似矩阵非常清晰.然而,其类内相似度完全一致,说明LRS对同簇数据不具备多态区分性,解释了其较弱的抗噪能力. 为进一步说明LRAFL的特征选择和数据聚类能力,采用人造的双半环数据进行效果验证.数据分为2簇,每簇100个样本点并随机叠加15%的高斯白噪声.图2显示了LRAFL在不同位置分布情形下的双半环数据特征选择结果,其中,图2(a)将数据左右放置,图2(b)将其投影至高特征权值对应的坐标轴,图2(c)是上下分布的数据,图2(d)同理将其投影至高权值对应的坐标.可见:当输入数据分别处于左右和上下分布时,LRAFL分别以横坐标和纵坐标作为高权值特征,说明其具有鉴别特征选择效果.此外,图3将双半环数据交叉放置,并采用RSS,LRS和LRAFL进行聚类对比,从中可见RSS和LRS两者的聚类结果都存在明显的错误,而LRAFL的聚类结果与输入簇结构完全吻合,表明其成功地将原始数据分成了2个类别,聚类效果优于RSS和LRS. Fig.2 Feature selection of LRAFL under different distribution of two-moon synthetic data图2 不同位置分布情形下的双半环数据特征选择结果 Fig.3 Clustering results on the two-moon synthetic data by RSS,LRS,and LRAFL图3 交叉分布情形下的双半环数据聚类效果对比 通过7个不同的数据集和11种算法验证LRAFL模型的聚类性能,即准确度(AC)[25]和归一化互信息(NMI)[31]两个指标.测试数据包含3个人脸数据集(Orl,YaleB[23],Jaffe[12])、1个语音字母数据集(Isolet)、2个生物数据集(Yeast,Lung)和1个对象数据集(Coil[12]).为方便横向对比,所有带参考文献的数据集都依原文进行预处理,余下数据则保持原始形式.表1给出了各数据集的细节描述.对比算法包含LLCFS[11],MCFS[8],NDFS[15],FSASL[12],LPS[13],kmeans[32],DEC[14],SMR[23],LRS[24],RSS[25]和NSLLRR[22]. Table 1 Summary of the benchmark datasets and the number of selected features表1 数据集描述和实验中的特征选择数 为获得各算法的最优实验结果,在实现时,需要对其人工参数进行网格搜索.在实验中,所有算法的正则参数和邻域参数范围分别设为{10−2,…,102}和{3,6,9,12,15}.表2和表3分别给出了所有对比算法通过10次随机初始化获得的准确度和归一化互信息指标.图4列出了各算法的平均AC和NMI指标. Table 2 Aggregated clustering results measured by AC (%) of the competing methods表2 所有算法在不同数据集下的聚类准确度指标对比 Table 3 Aggregated clustering results measured by NMI (%) of the competing methods表3 所有算法在不同数据集下的聚类互信息指标对比 Fig.4 Average clustering results measured by AC and NMI (%) of the competing methods图4 各算法的平均聚类准确度和归一化互信息对比 从表2和表3可知, · 首先,依据样本的分布结构及特征量差异,各算法的聚类性能落差较大.例如:Yeast数据集的维数较低,其类间间隔相对紧凑;而YaleB,Orl受光照、表情等影响较大.LRAFL在这3个数据集中的AC指标分别仅为49.73%,63.44%和61.50%.此外,Lung和Jaffe因为具有直观的分布结构比较容易实现聚类,其对应的LRAFL聚类AC指标分别达到了92.66%和99.20%; · 其次,对比经典的k-means算法,DEC,NDFS和FSASL等特征选择型算法都提升了聚类性能,而重构表示型算法,如SMR和NSLLRR则具有更加优秀的结果.RSS受表示系数次优解影响,性能落差较大,在YaleB中获得了65.78%的最高聚类精度,但在Jaffe和Orl中则仅获得了32.39%和21.25%的AC结果,逊于基准模型k-means; · 最后,LRAFL兼顾了特征优选机制和块对角Laplacian目标矩阵,其综合性能优于其他算法,在AC和NMI中分别赢得了4个和6个最高值,尤其在Jaffe和Coil中,分别获得了98.76%和97.05%的最高NMI.图4进一步表明,LRAFL在各数据上的综合AC和NMI指标高于其他算法. LRAFL聚类模型包含特征优选权值w和簇结构逼近投影矩阵F用于块对角结构的相似度矩阵S构建.为进一步评估各子项的贡献度以及联合w,S迭代更新的优势,将LRAFL算法分为无特征权值版(Nw)、无投影矩阵版(NF)、独立优化版Ind以及原始LRAFL模型(Ori),其中,Nw是对目标函数式(12)中的特征加权部分去除,联合优化S和F;NF指剔除公式(12)中的投影矩阵F,联合优化w和S.图5对比了4个版本在真实数据集中的准确度和归一化互信息指标.从图5可知,LRAFL原始版在所有测试数据中的聚类指标都高于其减化版本.此外,NF在各LRAFL减化版中效果最差,说明块对角Laplacian矩阵结构对聚类问题的关键性,与正文理论分析一致;Nw版的聚类效果略逊于Ind版,说明特征优选机制能改善聚类分析效果;最后,Ind版与Ori版的性能差距则进一步验证了LRAFL模型联合迭代更新的优势. Fig.5 Clustering accuracy and NMI w.r.t.different versions of LRAFL图5 不同版本的LRAFL算法准确度和归一化互信息对比 为进一步验证所提算法性能在不同特征选择量下的表现,图6将LRAFL与其他几种性能较优的特征选择算法进行对比,包括MCFS,NDFS,FSASL和DEC,选用的数据集为Jaffe和Lung,其中,前者的特征维数较少(676),后者的特征维数较高(3 312).从图6可见,LRAFL在不同特征空间中的AC和NMI指标都优于其他算法,说明自适应特征学习机制能够有效地区分输入高维特征的优劣,进一步优化性能.随着有效特征维数的增加,不同算法的聚类性能都有所提升.然而,当维数进一步增加时,冗余特征导致算法的性能不增反降.相比较而言,LRAFL除特征选择之外又添加了特征有效性加权机制,因此其精度曲线较为平坦. Fig.6 Clustering accuracy and NMI w.r.t.different selected features图6 不同特征寻优下的分簇准确度和归一化互信息对比 Fig.6 Clustering accuracy and NMI w.r.t.different selected features (Continued)图6 不同特征寻优下的分簇准确度和归一化互信息对比(续) 运行效率是算法应用能力的另一关键指标,本节选择在不同数据集中综合聚类性能表现较为突出的几种算法进行计算效率对比.指标测试时含参数优选过程,表4显示了各算法在各数据中的运行时间(单位:s). 算法运行平台为Intel Core i5 CPU,双核主频2.80GHz,内存4GB,32位Win7操作系统和Matlab2014b软件环境. 根据表4结果并结合表2、表3可知:LRAFL不仅在综合聚类效果上优于对比算法,而且其运行效率也具有明显的优越性.以Jaffe为例,LRAFL仅需要4.76s完成参数优选和聚类分析运算,而排名第2的NDFS算法则耗费了近80s时间.此外,部分表示型聚类算法,如SMR,RSS和NSLLRR,以运行效率为代价,在YaleB,ISOLET等数据集中取得了较LRAFL略优的聚类效果,但从表4可见,其运行时间呈指数级增长,基本较LRFAL慢10倍以上,尤其是NSLLRR模型,其综合聚类性能高于除LRAFL的其他对比算法,但是受非负系数矩阵构建以及多个人工可调参数影响,运行效率远远低于所有竞争算法,严重影响其应用扩展能力. Table 4 Aggregated results measured by elapsed time of the competing methods表4 所有算法在不同数据集下的运行效率对比 根据上述实验结果所示,所有聚类算法都有不同的人设参数待选,对算法应用效果和效率都有极大的影响.因此,所提算法的参数个数及其对不同设定值的敏感性是影响算法应用能力的又一指标.LRAFL算法有两个待选参数——邻域数k和正则数γ,图7给出了其在不同选值范围下的聚类准确度性能变化,选用的数据集包括YaleB,Jaffe,Yeast和Orl. 从图7结果可知:LRAFL算法的两个参数中,γ对不同选值的敏感度较小,而且其选择过程也较为直观.本文采用2x<300取值,其中,x∈{−1,2,4,8,16}.k对不同选值的敏感度较大,但具体应用过程中,k的取值范围非常清晰,一般以10为中心向两边测试,减少了应用难度.此外,邻域数k是所有算法的待定参数,如何对其进行优选仍是一个公知问题. Fig.7 Clustering accuracy of LRAFL w.r.t.different parameters图7 LRAFL参数优选下的聚类准确度 本文提出了一种新的数据聚类算法LRAFL,兼顾自适应特征优选和簇结构学习两个关键目标.特征优选通过输入数据的重构表示进行自适应权值计算,并依权值高低进行有效特征筛选.簇结构学习通过对Laplacian矩阵强制进行c秩约束,获得精确的数据相似度矩阵,直接进行c簇结构划分.LRAFL能够同时进行特征选择和数据聚类,且模型待设参数的物理意义明确,实现过程简洁直观.此外,设计了一种快速高效的模型求解算法,并给出了相应的算法复杂度分析和收敛性分析.通过大量人工合成数据和现实公开数据集验证了所提算法在精度、归一化互信息、运行效率和参数敏感度上较现存算法具有明显的优势.对比特征选择型算法,LRAFL在聚类效果和运行效率上都具有优越的实验结果;对比表示型算法,LRAFL虽然在部分数据集中无法获得更高的精度指标,但其运行效率却具有指数级的提升. 通过实验发现,所提算法LRAFL在应用过程中需要人工设定参数k和γ,虽然可以通过经验方式进行指引设置,且γ的取值对最终结果的影响较小,但仍然会削弱所提算法的应用扩展能力.因此,后续将集中进行待定参数的自适应确定或参数简化工作.此外,各聚类算法在不同的数据集中表现差异较大,不同先验样本分布对算法的性能影响仍不清楚,对其进行理论分析也是后续的工作之一.
3.2 收敛性和复杂度分析
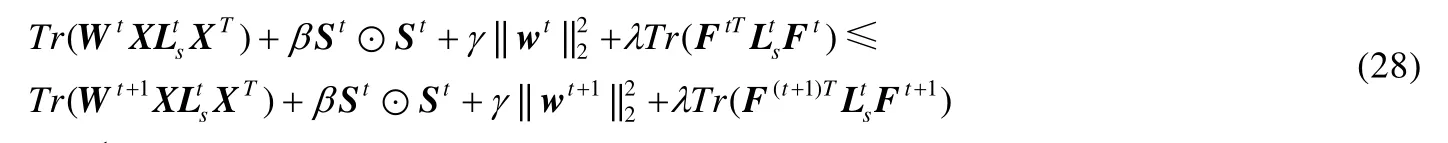

4 LRAFL算法描述
4.1 合成数据实验


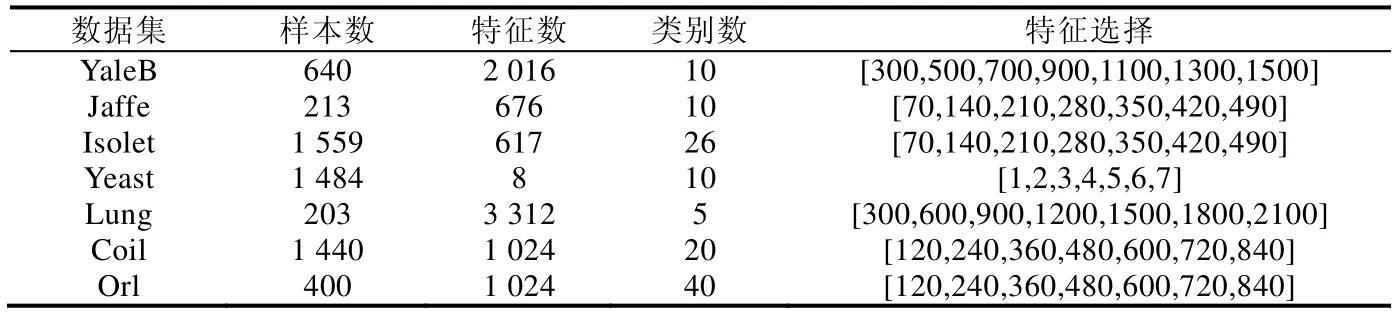
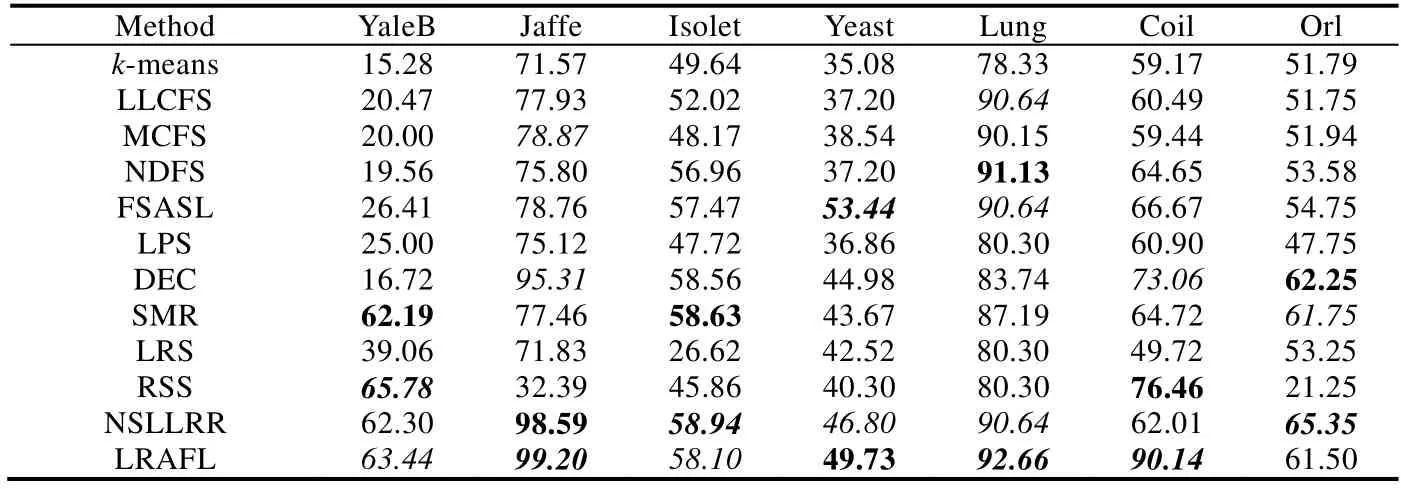
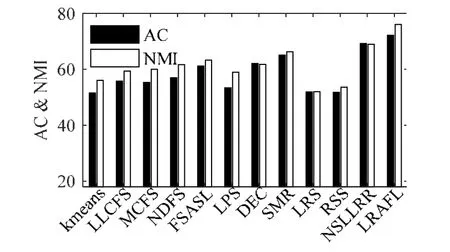
4.2 真实数据实验

4.3 算法效率分析

4.4 参数敏感度分析

5 总结

