极地船螺旋波纹管换热器强化换热分析与优化
张诗洁,徐 立,汤 冰,罗 梁,陈海文
(武汉理工大学 能源与动力工程学院,湖北 武汉 430063)
船舶在极地海域航行时,有必要对极地船的换热设备性能进行分析优化。螺旋波纹管是目前换热管强化换热技术发展与应用最充分的强化管之一,管壁上的螺旋凹槽能明显提高管内外流体的换热系数[1-4]。本文利用Fluent软件对优化后的螺旋波纹管与水平直管进行不同参数的仿真模拟与对比分析,研究不同工作环境下螺旋波纹管的最优结构以实现换热效率的最大化。
1 数学模型
1.1 强化换热模型
对流体传热进行强化时会牺牲摩擦阻力,引入综合强化因子(PEC)[5]对螺旋波纹管进行强化换热的效能分析:
PEC=(Nu/Nu0)/(f/f0)1/3,
(1)
式中:Nu和Nu0分别为强化后螺旋波纹管和水平直管的努塞尔数;f和f0分别为强化后螺旋波纹管和水平直管的摩擦系数。
1.2 管路流动换热方程
以努塞尔数(Nu)表征流动换热性能:
Nu=0.023Re0.8Prn,
(2)
式中:Re为雷诺数;Pr为普朗特数;本文管内流体放热,取n=0.3。
摩擦系数(f)的表达式为:
f=0.316 4Re-0.25(2×103 (3) (4) 水平直管采用D20×1 000 mm的光滑圆管,螺旋波纹管的几何模型如图1所示,其中波纹管总长1 000 mm,直径D=20 mm,波纹深度(h)选取1、2、3 mm,波纹宽度(w)选取2、4、6 mm,螺纹间距(p)选取8、10、12 mm。 图1 螺旋波纹管几何模型 在Hypermesh软件中进行网格划分,水平直管采用边长2 mm的六面体网格。螺旋波纹管采用边长1 mm的四面体网格,凹槽处网格加密,如图2所示,忽略壁厚条件。 图2 螺旋波纹管四面体网格 基于Fluent流体仿真软件,采用能量方程,RNGk-ε湍流模型,传热工质为海水。压力速度耦合采用Simple算法和一阶迎风格式的对流项,入口端湍流强度为8.6%,水力直径为19.27 mm,回流比为1,出口设定为压力出口。管外壁温度恒定,其他初始边界条件见表1。 图3为不同Re时PEC随h的变化关系。PEC随Re的提高而降低,在h较小(h=1 mm)时,PEC随Re的提高变化不明显,因为Re提高时边界层厚度降低,较小的h对边界层破坏小,提高强化换热效果有限。在低Re(Re=6×103)附近,中等h(h=2 mm)的强化换热效果更好。当Re提高(Re>1.2×104)后,较小的h(h=1 mm)强化换热效果更好,因为此时流动损失低且能抑制边界层的增长。而其他较大h的综合换热性能随Re的增大而降低,表示其流动损失的效果超过换热性能的增强。 表1 初始边界条件 图3 不同Re时PEC随h的变化关系 图4、图5分别为不同Re时f和Nu随h的变化关系。Re一定时,h增大,f升高,Nu增加,但不明显,说明h对f产生显著影响而对换热性能影响不大。这是因为h增大时,f随凹槽倒角的降低而降低,流体在凹槽处的局部损失降低,但加强了边界层对流体的强制扰动,提高了强化换热性能也提高了流动压降,增加了流动损失。 图6为不同Re时PEC随w的变化关系。Re一定时,PEC随w的提高而提高,w一定时,PEC随Re的提高而降低。可见波纹较宽的凹槽有利于换热,但随着Re的提高,其综合换热性能变化越发不明显,而中等w的综合换热性能表现更好,这是因为流体在凹槽处边界层较薄,适当扰动管内流体就能较好地强化换热,而w越大流体扰动越大,流动阻力也增大,不利于增强换热性能。 图4 不同Re时f随h的变化关系 图5 不同Re时Nu随h的变化关系 图6 不同Re时PEC随w的变化关系 图7、图8分别为不同Re时f及Nu随w的变化关系。Re一定时,随着w的增大,Nu无明显变化。证明w对强化换热影响很小,但对f影响较大,相同Re时,f随w的增大而下降明显,这是因为h不变而w提高相当于降低凹槽的倒角,从而降低了流体通过凹槽的局部损失。另外w的增大也强化了边界层流动,增大了流动压降,提高了局部流动损失,评价综合换热性能要考虑PEC与局部阻力损失两方面。 图7 不同Re时f随w的变化关系 图8 不同Re时Nu随w的变化关系 图9为不同Re时PEC随p的变化关系。p不变时,PEC随Re的提高而降低,因为Re提高使凹槽边界层的热阻降低,凹槽产生的压降效果强于强化换热的效果。另外,在较小的Re区间内提高p会降低PEC,因为此时热边界层较厚,凹槽产生的压降效果弱于对边界层的强化换热效果,此时采取较低的p更适合。虽然Re增加会降低边界层的厚度,增大p产生的强化换热效果强于产生的阻力损失,但在Re>1×104后,p的增大对强化换热性能的提升不再明显。 图10为不同Re时f随p的变化关系。Re一定时,p降低,边界层扰动产生的剪切应力提高,流体在近壁面处的流动阻力变大,f升高。另外,p不变,Re提高时,速度边界层降低,凹槽对边界层的流动阻力减小,影响也变小。图11为不同Re时Nu随p的变化关系。Re一定时,p的提高,凹槽对边界层的强化效果增强,边界层厚度减小,但凹槽产生的压降效果强于其强化换热的效果,因此流动换热性能降低。而p过小会导致边界层厚度提高,凹槽对边界层的限制效果降低,换热效果减弱。因此,选取合适的p才能达到螺旋波纹管的Nu最优解。 图9 不同Re时PEC随p的变化关系 图10 不同Re时f随p的变化关系 图11 不同Re时Nu随p的变化关系 利用MATLAB软件对螺旋波纹管的结构参数建立数学模型,将强化换热的影响参数转化成计算机语言进行求解以求得最优结构参数,目标函数fmin定义为: (5) 将本文折线图中螺旋波纹管的数据带入多元线性回归方程,得到: fmin=0.678 3Re0.163 4(h/D)0.467 2(w/ D)-0.241 9(p/D)-1.475 2。 (6) 通过MATLAB程序求解,最终得到目标函数方程的最小值fmin=0.416 8。即当螺旋波纹管参数结构为Re=2 000,h=2 mm,w=4 mm,p=8 mm时,强化换热性能最优,是水平直管的1.63倍。 1) 在一定范围内增大波纹深度或减小螺纹间距,均能增强螺旋波纹管换热性能,但同时增大了流动摩擦阻力。 2) 波纹宽度的变化对强化换热性能无明显影响,但其对流动摩擦阻力有较大影响,摩擦系数随波纹宽度的增大有明显提升。 3) 利用MATLAB求出强化换热性能最优的螺旋波纹管结构参数:h=2 mm,w=4 mm,p=8 mm,该参数下螺旋波纹管综合换热性能是水平直管的1.63倍。2 几何模型与计算条件
2.1 几何模型及网格划分
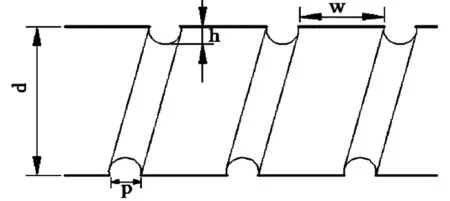

2.2 边界条件
3 模拟结果
3.1 波纹深度对流动换热的影响

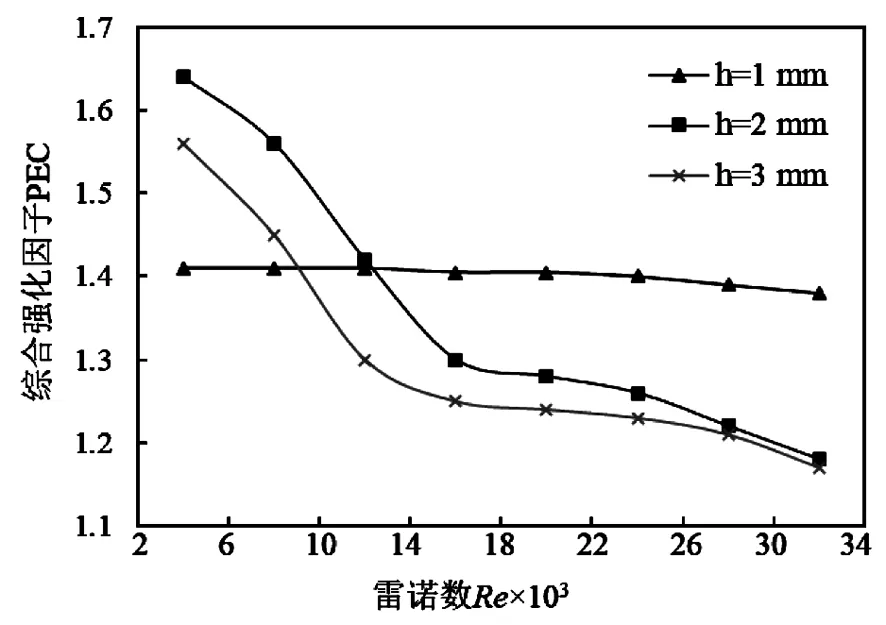
3.2 波纹宽度对流动换热的影响





3.3 螺纹间距对流动换热的影响

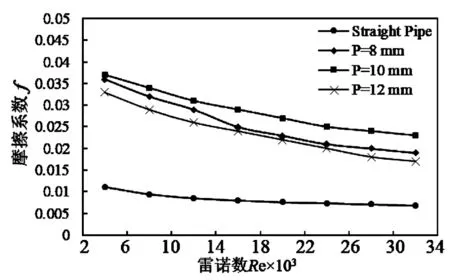
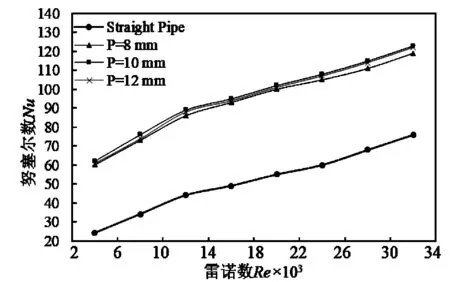
3.4 MATLAB最优结构优化设计计算
4 结束语

