面心立方Ce同构相变的分子动力学模拟

第伍旻杰 胡晓棉

1) (中国工程物理研究院研究生院,北京 100088)

2) (北京应用物理与计算数学研究所,计算物理国家重点实验室,北京 100088)

基于嵌入原子法,本文给出了一个金属Ce原子间的相互作用势.利用该势分别计算了γ-Ce和α-Ce的晶格常数、结合能、弹性常数,计算结果与实验或第一性原理研究中得出的数值符合得较好.给出了两相Ce中如点缺陷形成能、表面能、层错能以及孪晶能等晶体缺陷形成能.通过分析两相Ce的声子谱,得出了不同温度下两相的晶格振动熵差,其中在室温条件下约为0.67kB/atom.还利用分子动力学模拟得出了该相变的等温线,并且利用径向分布函数分析了相变前后两相的晶体结构,确认了该相变为面心立方同构相变,即Ce的α-γ相变.由此表明,本文的嵌入原子法势,不仅可以分别合理地描述γ-Ce和α-Ce,还可以反映γ-Ce和α-Ce两相之间的相变.

1 引 言

铈(cerium,Ce)是一种稀土金属元素,其f电子处于局域与非局域的转变点上,具有低熔点、非对称晶体结构、多种同素异形体共存、发生相变伴随体积变化等物理、化学性质[1,2].Ce及其稀土合金已广泛应用于钢铁、有色金属及其合金、发火合金、稀土永磁合金、储氢材料等诸多领域[3].

在较低的温度和压强条件下,金属Ce有两种面心立方(FCC)相(α相和γ相)以及一种双密排六方相(β相)[4].在室温和0.7GPa压缩条件下Ce会发生γ → α同构相变[4-6],晶格常数从5.16 Å突变到4.84 Å,同时体积减小14%-17%.α-γ相变的临界点(C.P.)压强PC=1.44-1.96 GPa[4,7,8],温度TC=460-600 K[4,7,8].

作为Ce的α-γ相变的机制,从电子结构来看,Mott相变和Kondo体积坍缩(KVC)两种理论模型长期争论不下[4,9,10].也有研究认为,这两种模型分别反映了Ce的α-γ相变的不同侧面[11].除此之外,Amadon等[12]认为在室温条件下熵的效应不可忽略,Ce的α-γ相变是由熵驱动的.而熵的贡献可分为电子的和晶格振动的两个自由度.利用高压高分辨率同步X射线粉末衍射实验,Jeong等[13]测得Ce的α-γ相变过程中,晶格振动的熵变(ΔSvibα-γ≈(0.75 ± 0.15)kB/atom)约占总熵变(约1.54kB/atom)的一半.Wang等[6]利用第一性原理计算得出的总熵变约为2.86kB/atom,其中晶格振动的熵变约为0.94kB/atom.这些都表明晶格振动的熵变在总熵变中占据相当可观的一部分.

对于Ce的α-γ相变,以往的模拟计算工作中主要分宏观数值模拟和第一性原理电子结构计算两方面.基于多相物态方程的宏观数值模拟[14-16]无法给出相变过程中微尺度结构的细节; 而相关的第一性原理计算[6,11,17-19]受制于其时间和空间尺度,只能对此相变进行均匀、平衡态的分析.而非平衡态分子动力学模拟因其特点,可以在微、纳米尺度提供更多的信息,如相变过程中微结构的演化,从而可以将离散原子尺度与宏观尺度沟通起来.

在分子动力学模拟中,分子间相互作用势必不可少.已有工作中针对FCC结构Ce的经验势不多：例如Singh和Singh[20]将两体作用的杂化近自由电子紧束缚成键模型用在一些FCC结构的稀土金属(包括Ce),得出的结果在声子谱和弹性常数等方面与实验符合较好; Hachiya和Ito[21]在此基础上利用近自由电子键角相关紧束缚成键模型(最早用于过渡金属及其合金)进行了改进; Sheng等[22]利用势能面拟合法,得出了包括Ce的14中FCC结构金属的嵌入原子法(EAM)势; Fu和Zhao[23]拟合了FCC镧(La)和Ce的Gupta势.虽然这些经验作用势都与Ce的实验和第一性原理的数据符合得很好,但只涉及了γ-Ce,而与α-Ce无关,因此无法用于Ce的α-γ相变的分子动力学模拟.Voter和Chen[24]通过对Voter-Chen EAM进行修正,提高两相之间的势垒(0.142 eV/atom)来维持各相的稳定性,提出过一种能够描述Ce的α-γ相变的经验势[25,26],不过该势的具体描述至今未见发表.为了能够对Ce的α-γ相变进行大规模分子动力学模拟,本文展示了一种新的FCC结构Ce的EAM势,该势可对γ-Ce,α-Ce以及Ce的α-γ相变进行合理描述.

2 EAM模型势的构建

α-Ce和γ-Ce的冷能曲线可以分别用Rose物态方程来表示[25,27],也就是说FCC结构Ce的冷能曲线应当是一个分段函数：晶格常数较大的部分为γ-Ce的Rose曲线,晶格常数较小的部分则为α-Ce的Rose曲线.两段各有一个极小值点对应于各相平衡位置的晶格常数,两段曲线交叉于两极小值点中间形成一个势垒.

在嵌入原子法中,单类型原子系统的总势能Etot可以表示为

其中Φ(rij)为原子i与j之间的对势,F为原子i处于电子云密度ρi的嵌入能,f(rij)为原子j在原子i处的电子密度分布函数.

在文献[28]中,嵌入能F和电子密度ρ的关系表示为

式中a,b,c为待定参数.Φ(rij)和f(rij)的解析形式为立方项求和：

可以根据精度要求选取n的上限,an,rn,bn,sn为待定参数; Θ(x)为Heaviside函数,若x ≤ 0,Θ(x)=0; 若x＞0,Θ(x)=1.已经有研究将其用于拟合面心立方金属的原子间相互作用势.在本文工作中先对Φ(rij)和f(rij)分别只取一项,即

且令bγ=1 Å-3,sγ=6.6 Å (此即相互作用势的截断距离).利用最小二乘法,以γ-Ce的Rose物态方程曲线和弹性常数为目标对(2)式-(4)式中的参数a,b,c,aγ,rγ进行拟合.由此得出的γ-Ce的冷能曲线与α-Ce的Rose物态方程曲线相交于r=3.498 Å,于是对Φ(r),f(r)和F(ρ)函数应当采用分段函数的形式(分段点为r=3.498 Å,ρ=389.094).由于势函数的长程部分(r＞3.498 Å)已经确定,接下来只能调整短程的部分(r ＜ 3.498 Å).在r ＜ 3.498 Å的范围内仍采用相似的形式,同时为了保证势函数的连续性,则有

嵌入函数F(ρ)则通过嵌入能F (即总势能与对势能部分之差)与电子云密度ρ的对应关系利用立方样条插值得出.(5)式和(6)式中的参数aα,rα,Φ0,bα,sα,f0参照α-Ce的Rose物态方程曲线和弹性常数,并考虑α-γ相变的温度和压强条件来确定.最终的对势函数Φ(r)、电子密度函数f(r)、嵌入能函数F(ρ)如图1(a)和图1(b)所示.

图1 Ce的EAM势 (a)对势函数和电子密度分布函数; (b)嵌入能函数Fig.1.EAM potential for Ce：(a) The pair function Φ(rij) and the density function f(rij); (b) the embedded function F(ρ).

3 结果与讨论

为了验证第2节中所得的EAM势,本文采用了LAMMPS[29]对面心立方Ce晶体的一些性质以及α-γ相变过程进行了分子动力学模拟计算.

3.1 基本性质

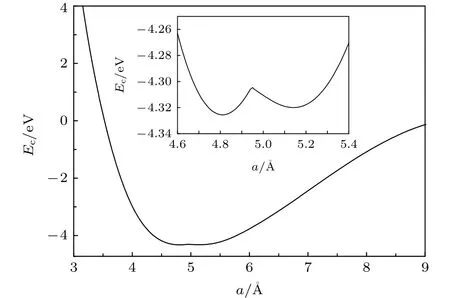
图2 由本文EAM势得出的面心立方Ce的冷能曲线Fig.2.The cold energy of fcc Ce calculated with the newly developed EAM potential.

图2展示了由EAM势计算得到的Ce的冷能曲线.该曲线分为两段,每段各有一个极小点,分别对应于α-Ce (a=4.81 Å)和γ-Ce (a=5.14 Å).可以看出,在两个极小值点中间存在一个高度为15.3-20.8 meV/atom的势垒,远小于Chen等[25]的经验势中的对应值(0.142 eV/atom).表1中展示了由EAM计算得出的α-Ce和γ-Ce的一些基本性质,包括晶格常数、结合能、弹性常数等,与实验或第一性原理计算的结果符合得很好.

3.2 晶体缺陷

3.2.1 点缺陷

为了定量地研究在Ce中的点缺陷,采用本文的EAM势在10×10×10 的FCC超胞中计算了α-Ce和γ-Ce中的空位和填隙原子的形成能.晶体点缺陷的形成能(Ef)的定义为

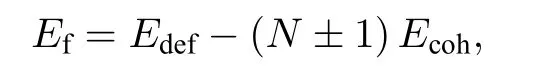
其中Edef为包含单个点缺陷超胞的最小化总能量,N为无缺陷超胞的原子数(在此N=4000).于是正号对应于填隙原子,负号对应于空位.Ecoh为无缺陷晶体中单个原子的结合能.

表1 面心立方Ce的基本性质的EAM计算值与实验和第一性原理结果的比较Table 1.EAM predicted properties of Ce lattice in comparison with experimental and ab initiodata.

对于γ-Ce,填隙原子和空位的形成能分别为1.93和0.85 eV,分别对应于无缺陷单晶中单个原子结合能的44.7%和19.7%; α-Ce中的填隙原子和空位的形成能分别为2.97和1.15 eV,分别对应于无缺陷单晶中单个原子结合能的68.7%和26.6%.以往的研究中所得的FCC过渡金属的空位能约为1-3 eV[35],这里所得的填隙原子和空位的形成能处在与之可比的范围内,可以认为是合理的.

3.2.2 表面能

采用本文的EAM势同时通过Polak-Ribiere共轭梯度法[36]对表面构型进行充分弛豫,以此计算了α-Ce和γ-Ce的三种低密勒指数(即(100),(110)和(111))晶面的表面形成能,计算结果列在了表2中.对于γ-Ce本文中计算所得的表面能明显低于以往经验势的计算结果[22,23].不过两相Ce中的表面能的大小顺序都符合γ(111)＜ γ(100)＜γ(110),表明其中(111)表面最稳定,这方面与Sheng等[22]以及Fu和Zhao[23]对γ-Ce的计算相结果相一致.比较α-Ce和γ-Ce相同晶向的表面能,则有γα＜ γγ,如对于(100)晶面γα(100)＜ γγ(100),另外对于γ(110)和γ(111)亦同.到目前尚未见关于金属Ce表面能实验测量结果的报道,本文的表面能数值可作为未来相关测量实验的参考.

3.2.3 面缺陷

材料的稳定和非稳定层错能被认为是决定其力学行为(如金属的塑性变形)的重要物理量.利用本文的EAM势计算得出了α-Ce和γ-Ce中堆垛层错和(111)孪晶缺陷的广义面缺陷能曲线.广义层错能曲线可通过对无缺陷单晶沿(111)晶面进行刚性剪切得到,而广义孪晶缺陷能曲线则可通过对预置层错的无缺陷单晶进行刚性剪切得出.最终α-Ce和γ-Ce中的广义层错能曲线和广义孪晶能曲线分别如图3(a)和图3(b)所示.

由此可得γ-Ce的非稳定层错能γusf=0.543 J·m-2,稳定层错能γssf=0.457 J·m-2(与Sheng等[22]利用EAM计算的结果相近); 而在α-Ce中γusf=0.821 J·m-2,γssf=0.734 J·m-2.虽然此处的结果与Östlin等[37]的第一性原理计算结果相差较大,但是对比α-Ce和γ-Ce两相的稳定层错能和非稳定层错能均满足γγsf＜ γαsf.Swygenhoven等[38]认为要了解FCC晶体变形的机制仅有非稳定层错能或者稳定层错能都是不全面的,还应当比较稳定层错能与非稳定层错能的比值γssf/γusf.该比值接近于1的时候倾向于越过整个势垒产生全位错; 反之若该比值较小则倾向于产生偏位错(作为参考,在Al中该比值为0.97,在Ni中为0.55,在Cu中为0.13).在γ-Ce中γssf/γusf=0.842,α-Ce中γssf/γusf=0.875,数值较高,与Al中的比值比较接近.因此可以推测本文的EAM势在MD模拟的FCC结构Ce塑性变形中有可能观察到全位错产生.

表2 γ-Ce and α-Ce中晶体缺陷的形成能Table 2.Calculated formation energy of lattice defectsin γ-Ce and α-Ce.

图3 面心立方Ce中的广义层错能和广义孪晶能 (a) α-Ce; (b) γ-CeFig.3.Generalized stacking fault energy and generalized twining fault energy curve for (a) α-Ce and (b) γ-Ce.

除位错激活与滑移之外,形变孪晶是FCC结构晶体的另一种形变机制.由本文EAM势计算得出的非稳定孪晶能γutf,在γ-Ce中γutf=0.768 J·m-2,在α-Ce中γutf=1.167 J·m-2.Tadmor和Hai[39,40]发现形成形变孪晶的趋势与比值γutf/γusf相关,该比值越高越不容易产生形变孪晶.对于γ-Ce,γutf/γusf=1.414; 对于α-Ce,γutf/γusf=1.420,均接近且高于其在Al中的比值(约1.3).由此可推测利用本文EAM势进行MD模拟很难出现形变孪晶.

3.3 晶格动力学

3.3.1 声子态密度和晶格振动熵

图4所示为温度T=300 K条件下晶格常数分别等于4.89 Å (α-Ce,压强约0.7 GPa)和5.16 Å (γ-Ce,零压)状态的声子态密度.两相的态密度有显著差异：1)“肩部”由1.21 THz (γ-Ce) 移动到了 1.43 THz (α-Ce); 2)后续增长的尖峰由1.81 THz (γ-Ce) 移动到了 2.31 THz (α-Ce);3)再之后的峰由2.58 THz (γ-Ce)移动到了3.36 THz (α-Ce).

Ce的α-γ相变被认为是由熵驱动的,也就是说熵在其中扮演重要位置.利用图4中的态密度,可以分别计算出两种状态的晶格振动的熵(如图5).图5中右下角虚线图为两种状态的晶格振动熵的差值,温度T=300 K时的熵差为ΔSvib=0.67kB/atom,此与Jeong等[13]的结果(0.75 ±0.15)kB/atom相近.然而由于经典分子动力学模拟的特性,无法给出电子结构自由度对熵的贡献,在此对Ce的α-γ相变过程的经典分子动力学模拟中只能将固体系统的熵全部归于晶格振动自由度.于是本文工作中分子动力学模拟的Ce的α-γ相变过程的总熵变等于晶格振动熵变,即ΔS=ΔSvib=0.67kB/atom (此值较实验值1.54kB/atom少约0.87 kB/atom).

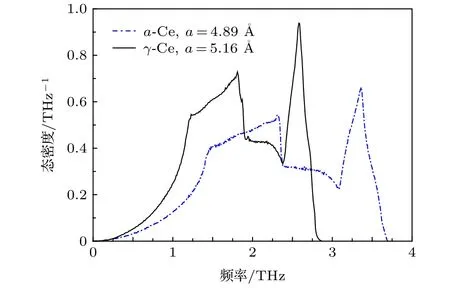
图4 面心立方Ce的声子态密度Fig.4.Phonon density of states for FCC Ce.

图5 α-Ce和γ-Ce两相的晶格振动熵Svib以及熵差ΔSvib(右下插图)随温度T的变化Fig.5.The vibrational entropy Svib and its change ΔSvib between two phases (the inset) plotted as functions of temperature.

3.3.2 声子色散谱

利用声子色散曲线可以更严格地检验经验作用势.图6所示为300 K温度条件下计算利用本文EAM计算所得α-Ce (a=4.89 Å,黑实线) 和γ-Ce(a=5.16 Å,蓝色点虚线) 的声子色散关系谱.两相均有三支声学波,其中一支为纵波,另两支为横波.之前的实验和理论研究中发现对于γ-Ce在[ζζζ]方向横波的L点处存在反常下沉(软模)[6,19,41].而本文计算中无论α-Ce还是γ-Ce均未找到此反常下沉.

图6 面心立方Ce的声子色散谱Fig.6.Phonon dispersion relations for FCC Ce.

3.4 α-γ相变

利用本文中的EAM势并通过分子动力学模拟研究了Ce的α-γ相变.对初始为FCC结构的Ce进行静水压(各向同性)加载,计算所得的压强-体积等温线如图7(a)-图7(c)所示,其中图7(a)和图7(b)的等温线由NPT系综分别增、减压强得出,图7(c)的等温线由NVT系综弛豫得出.如在温度为T=300 K的条件下,增大压强到0.80 GPa时发生相变,体积突变减小2.68 Å3/atom; 反之,减小压强到0.59 GPa时发生逆相变,体积突变增大2.83 Å3/atom.由此看出300 K温度条件下存在明显的(0.21 GPa)迟滞.当温度升高至约550 K时,图7(a)和图7(b)中的等温线变为光滑曲线,体积随压强连续变化.对应图7(c)中的极小值点与极大值点重合于拐点处,此时拐点的斜率为零.当达到更高的温度,如600,700和800 K时,拐点的斜率变为负值.由此得出临界点温度Tc≈550 K,压强Pc≈1.21 GPa.根据图7(a)和图7(b)绘出的静水压加载下该相变的温度-压强相变路径如图8所示,此可视为该相变的P-T相图.

为了确认该相变否是为Ce的α-γ同构相变,利用径向分布函数对相变前后的晶格结构进行了分析.图9中比较了温度为300 K时不同压强加载下的径向分布函数：零压加载下的前三个峰值对应的间距值分别为3.62,5.16 和6.30 Å; 增压加载当压强增大至0.7 GPa (图7中A点所指状态) 时对应的这三个间距值分别为3.56,5.06 和6.18 Å;减压加载当压强降至0.7 GPa时 (图7中B点所指状态) 对应的这三个间距值分别为3.42,4.89和5.98 Å.这三种不同加载情况下的径向分布函数均符合FCC结构的最近三阶近邻间距之间的关系.于是可以认为相变前后的两相均为FCC结构,以上模拟的相变正是Ce的α-γ同构相变,其中晶格常数较大的一相对应于γ-Ce,而晶格常数较小的一相对应于α-Ce.也就是说,本文的EAM势可以用于FCC结构Ce的α-γ同构相变的分子动力学模拟,对α-γ同构相变进行多尺度的研究.

图7 面心立方Ce的等温线 (a) NPT增压; (b) NPT减压; (c) NVTFig.7.Isotherms of FCC Ce：(a) NPT,pressure increased; (b) NPT,pressure decreased; (c) NVT.

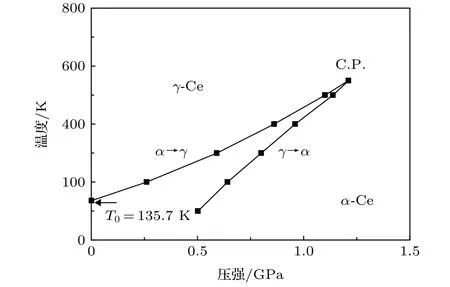
图8 Ce的γ→α和α→γ相变路径Fig.8.The path of Ce γ→α and α→γ phase transition.

图9 零压以及图7中A,B两点状态的径向分布函数Fig.9.Radial distribution function for zero pressure(black),the A state (red),and the B state (blue) pointed in Fig.7.

4 结 论

根据Rose物态方程还有弹性常数等实验以及第一性原理计算数据,本文给出了FCC结构Ce的EAM势.利用该EAM势对两种FCC结构Ce进行了定量的讨论.计算得出的两相Ce的结合能、弹性常数等一些基本性质,以及晶体缺陷和声子谱,与实验和第一性原理计算的结果符合较好.此外该EAM势可以用于FCC结构Ce的α-γ同构相变的分子动力学模拟,并且通过MD模拟得出的P-T相图也与实验相符合.

需要注意的是,以往的研究中表明Ce的α-γ相变是熵驱动的(特别是当处在室温条件下),其中包括了电子自由度和晶格振动自由度两个方面.但由于分子动力学模拟的局限性,无法体现电子自由度在其中的贡献,只能给出晶格振动方面的影响.本文中计算得出的常温下两相的晶格振动熵差约为0.67kB/atom.

本文的EAM势主要针对的是FCC结构的α-Ce和γ-Ce以及Ce的α-γ同构相变,未考虑到其他的因素.如同样处于较低的温度和压强条件下的β相,以及温度较高时的δ相(体心立方结构)和液态相.对此需要在后续的工作中考虑并改进.