基于LReLU-Softplus激活函数的深度卷积神经网络
林长方,黄毓珍,陈定柱,黄仲开
(1.漳州卫生职业学院健康与保健系,福建 漳州 363000;2.福建医科大学附属漳州市医院病理科,福建 漳州 363000;3.福建医科大学附属漳州市医院胸心外科,福建 漳州 363000;4.漳州卫生职业学院现代教育技术中心,福建 漳州 363000)
1 研究背景
近十几年来,深度卷积神经网络(convolutional neural networks,CNNs)在图像处理和语音识别等领域得到广泛的应用,取得令人瞩目的成绩[1-3]。激活函数作为CNNs的基本单元,可有效抑制网络反向传播过程中的残差衰减,并缩短模型训练时间,提高收敛速度,是CNNs取得成功的主要因素[4]。常见的激活函数包含饱和非线性函数(Sigmoid、Tanh)和不饱和非线性函数(Softplus、ReLU)。饱和非线性激活函数在传统神经网络中曾得到广泛的应用,但因其不能有效地解决函数由于饱和性而产生的梯度消失问题而最终被舍弃[5]。不饱和非线性函数可有效抑制算法运行过程中的梯度消失问题,且网络收敛速度快,是当前广为流行的激活函数[6]。然而,修正线性单元(rectified linear unit,ReLU)可能导致网络出现“坏死”现象,网络非常脆弱[7]。LReLU(ReLU-Leaky)、PReLU(Parametric ReLU)[8]等ReLU变形函数因带有稀疏性解决了ReLU的“坏死”现象,但它们同ReLU一样都是对模型的线性修正,因此都存在对模型表达能力弱的缺陷。Softplus函数为ReLU的非线性表达,但不具备稀疏性[9-11]。本文分析了两类激活函数的优缺点,并基于Softplus和LReLU函数提出了一种新的激活函数LReLU-Softplus,该函数兼具较强的稀疏能力与表达能力,且收敛能力强,识别率高。
2 常见激活函数及特征
激活函数的主要功能是对CNNs卷积操作的非线性建模,影响模型训练中的前向与反向传播两个过程。常见激活函数的公式及函数曲线如下所示。
2.1 饱和非线性函数
Sigmoid函数:f(x)=1/(1+e-x)。
Tanh函数:f(x)=(ex-e-x)/(ex+e-x)。
从Sigmoid函数表达式和图1可发现,函数f(x)的值域在(0,1)间,输入量x取值在0附近时,激活函数对信号的增益效果较明显。但当x越来越大或越来越小时,曲线越来越平缓,斜率越趋近于0,说明函数对信号的增益趋近于0,此特性将导致在反向传递过程中梯度的消失,最终致使网络参数难于得到有效的训练。另外Sigmoid函数非中心原点对称、均值偏移(即{∀x,y=f(x)≥0}),将致使函数在面对较深网络时训练无法收敛。
Tanh函数为Sigmoid函数的改进函数,从图1可见Tanh曲线以0为中心,f(x)的值域在(-1,1)间,因此,它缓解了均值偏移、训练收敛的速度加快。但它与Sigmoid函数一样具有软饱和性,同样存在梯度消失的缺陷。

图1 饱和非线性函数曲线

图2 不饱和非线性函数曲线
2.2 不饱和非线性函数
Softplus函数:f(x)=ln(ex+1)。
ReLU函数:f(x)=max(0,x)。
LReLU、PReLU、RReLU函数:f(x)=max(ax,x)。
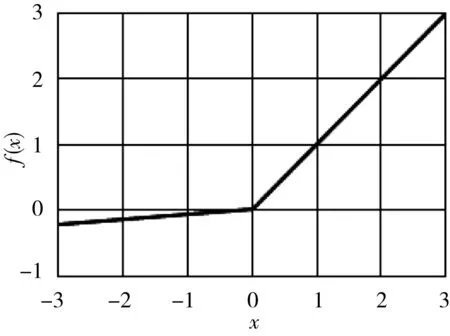
图3 LReLU、PReLU、RReLU函数曲线

图4 LReLU-Softplus函数曲线
不饱和非线性函数已成为当前构建深度卷积神经网络首选的激活函数,从图2、图3可发现Softplus、ReLU、LReLU等均有效解决了饱和非线性函数梯度消失的问题,但从函数表达式及曲线图可以看出它们各自都存在缺陷。ReLU及变形函数LReLU、PReLU、RReLU均为分段函数,ReLUs函数强制将输入值x小于0的输出结果置为0,从而使网络具有稀疏表达能力,可有效缓解过拟合的发生。但稀疏性会致使模型的有效容量降低,可能产生“坏死”现象。LReLU等变形函数是对ReLU函数的变形,当输入值x小于0时不再强制置输出为0,而是输出ax(a为一个很小的常数),这样使得负激活可在CNNs中得到传播,提高特征学习的效率。然而变形函数与ReLUs一样存在一个缺陷,即在x大于0时只能对数据进行线性映射,所以此类激活函数对CNNs的表达能力有欠缺。Softplus函数是对ReLU函数近似光滑、非线性的表示,可对所有数据进行非线性的映射,但稀疏表达能力欠缺。
3 LReLU-Softplus激活函数
结合LReLU和Softplus函数自身的优势,本文提出了一种新的不饱和非线性激励函数LReLU-Softplus,基本原理为:先将Softplus函数曲线向下平移ln2个单位,然后将输入值x小于0的输出置换为LReLU函数的ax,LReLU-Softplus函数公式及曲线为:
由图3可见,LReLU-Softplus函数保留了部分负轴数据,修正了数据的分布,继承了ReLU函数收敛速度快的优点,同时缓解了出现“坏死”的概率。更重要的是实现了函数的非线性、光滑映射。因此,LReLU-Softplus函数兼具稀疏表达能力和广泛、非线性映射性。
4 实验及结果分析
为了验证基于LReLU-Softplus函数的CNNs模型的执行效率,本文以MNIST和CIFAR-10为实验数据库,将卷积层分别使用LReLU-Softplus函数和常见激活函数的CNNS模型进行对比实验。实验在Matlab 2014a开发工具,基于Caffe框架的CNN环境下完成。硬件配置:Intel 酷睿i7 6700@3.4GHz 四核CPU,16G DDR4 2133MHz内存,4G AMD Radeon R9 370性能级独立显卡;64 bit windows 10 OS。
4.1 MNIST实验与结果分析
手写罗马数字数据集(MNIST)由训练图片(60 000幅)和测试图片(10 000幅)构成,图片均为28×28的灰度图像。实验所构建的CNNs模型架构及参数如表1所示,采样层的池化固定采用max-pooling方法,卷积层分别采用Sigmoid、Tanh、Softplus、ReLU和LReLU-Softplus作为激活函数。对LReLU-Softplus函数中的常量a分别选取0.01、0.02、0.05、0.1、0.2、0.5、1、2八个常量进行测试,测试结果如表2所示,从表2可见a=0.1时测试取得最好的性能。选取最合适的常量a,基于不同激活函数的CNNs在MNIST上的实验结果如表3、图5所示。

表1 MNIST实验CNNs架构

表2 LReLU-Softplus函数常量a测试结果

表3 不同激活函数实验结果
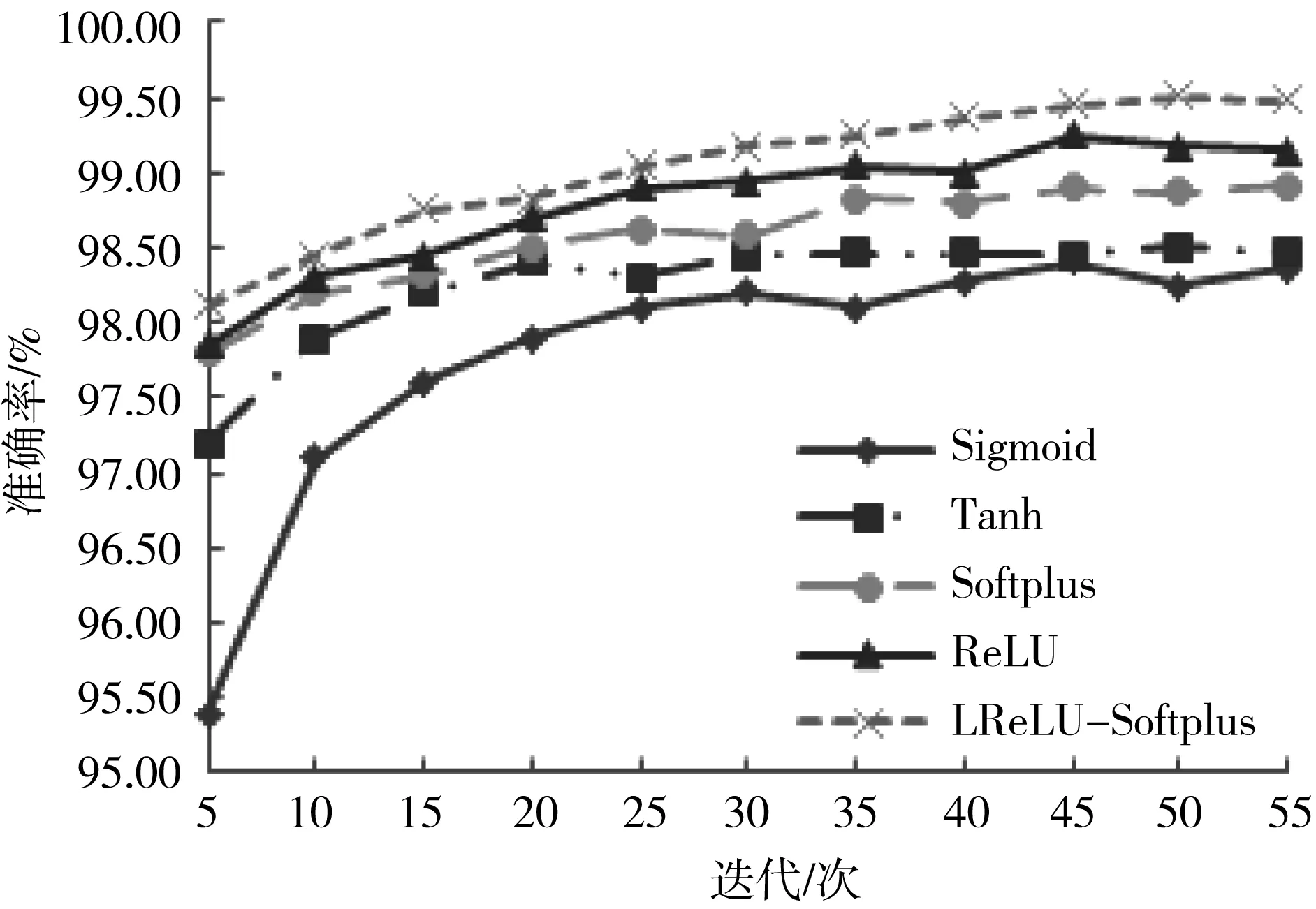
图5 不同激活函数识别正确率
观察表3、图5可发现,基于Sigmoid函数的网络不仅收敛速度缓慢且识别正确率只有98.40%;Tanh函数虽能使网络的收敛速度提高,但识别正确率也仅为98.51%;基于Softplus函数的网络较Sigmoid、Tanh函数收敛速度有所提升,识别正确率达到98.90%;使用ReLU函数的网络收敛速度进一步提高,识别正确率最高达到99.25%。而基于LReLU-Softplus函数的CNNs网络识别正确率、最佳验证误差、最佳测试误差分别达到99.51%、0.95%、0.86%,各项均为最佳值。
4.2 CIFAR-10实验结果与分析
CIFAR-10数据库由10个不同类型的彩色图像构成,分为训练图片集(50 000幅)和测试图片集(10 000幅),图片大小均为32×32,每个像素点包含R、G、B三个数值。本实验利用Y=0.3R+0.59G+0.11B(Y为YUV彩色空间中的亮度)对图像进行灰度级的转换,然后对图像进行ZCA白化处理,以降低图像特征之间的相关性,并利用Matlab对图像进行归一化处理。实验所构建的CNNs模型架构及参数如表4所示,采样层池化分别采用mean-pooling、max-pooling方法,卷积层使用不同的激活函数,CNNs对CIFAR-10数据集的分类识别最佳验证误差和测试误差如表5所示。

表4 CIFAR-10实验CNNs架构

表5 CIFAR-10实验结果
观察表5可发现,不论采用最大值或平均值池化,相较于其他常见激活函数,基于LReLU-Softplus激活函数的CNNs对CIFAR-10数据集的分类识别最佳验证误差和最佳测试误差均为最低。
实验结果表明,基于LReLU-Softplus函数的卷积神经网络在MNIST和CIFAR-10数据集上均取得较其他常见激活函数更低的误差率。其中,在MNIST数据集上的最佳验证误差达到0.95%;而在CIFAR-10数据集上,不论选择哪种池化方法,最佳验证误差和最佳测试误差均较其他常见激活函数降低了1%~2%。
5 结语
本文针对深度卷积神经网络卷积层中常使用的激活函数可能存在“坏死”现象、表达能力不足、欠缺稀疏能力或不易收敛等缺陷,设计了一种新的不饱和非线性激励函数LReLU-Softplus。通过在MNIST和CIFAR-10数据集上的实验表明,基于LReLU-Softplus函数的深度卷积神经网络不仅收敛速度快,而且识别效率更高,误差率更低。

