融合多种数据信息的餐馆推荐模型*

戴 琳,孟祥武,张玉洁,纪威宇

1(智能通信软件与多媒体北京市重点实验室(北京邮电大学),北京 100876)

2(北京邮电大学 计算机学院,北京 100876)

通讯作者:孟祥武,E-mail:mengxw@bupt.edu.cn

随着GPS 在手持设备的广泛应用,基于位置社交网络[1-5]的服务应运而生,并且已经达到了一种前所未有的水平.在基于位置社交网络的服务上,用户可以签到自己的位置,并分享自己的评价.推荐系统通过用户的这些隐式反馈(签到信息)和显式反馈(用户的评分和评论)挖掘用户的偏好,就可以为用户生成兴趣点推荐列表.这种基于位置社交网络的兴趣点推荐系统有很多,典型的包括美国最大的点评网站 Yelp(https://www.yelp.com/sf)、基于用户地理位置的手机服务网站 Foursquare(https://foursquare.com/)以及国内的大众点评(http://www.dianping.com/)等,这些网站通过分析用户签到及评论信息等,挖掘用户个性化偏好,为用户提供合适的选择,从而为用户带来便利,同时为商家带来可观的利益.本文所研究的餐馆推荐是兴趣点推荐中一个典型的应用.

餐馆推荐可以利用多种数据信息挖掘用户的饮食偏好,为用户生成餐馆推荐列表.从文献[6,7]可知:除了用户的显式反馈(评分、评论等)和隐式反馈(签到)直接反映了用户的偏好,还有以下因素也影响用户的餐馆选择:(1)时间上下文,在不同时间段用户的饮食偏好是不同的;(2)地理上下文,用户通常会选择活动区域附近的餐馆;(3)用户的人口统计信息,例如,不同年龄或不同性别的用户对于餐馆的需求是不同的,有的人看中服务,有的人看中环境等;(4)餐馆的属性信息,例如,用户对于餐馆的选择通常集中在某几类风格.因此,如果能够同时考虑这些数据信息,并有效地进行整合,挖掘这些信息的最大价值,就能够提高推荐精度.

文献[8]考虑了用户行为的空间聚类现象,提出一种结合地理位置信息的矩阵分解模型,该模型在加权矩阵分解的基础上引入了地理上下文,将用户的活动区域向量融合到用户隐式空间中,将兴趣点的区域影响向量融合到兴趣点隐式空间中,通过这种融合,有效地解决了矩阵稀疏性问题,从而提高了推荐准确度;但是该模型没有考虑时间上下文信息,也没有考虑其他元数据信息.

文献[6]基于用户的隐式反馈提出了一种隐式偏好模型,该模型同时考虑了时间上下文、地理上下文以及餐馆属性信息,分别利用概率张量分解和逻辑回归获得用户的隐式偏好.该方法能够很好地提高推荐准确度,但是该方法是分别对各数据信息相对独立地进行分析,缺乏对所有数据信息进行有效地融合,且时间复杂度高.

文献[9]考虑到用户存在一些依赖关系,而用户的这些关系会相互影响用户的偏好,因此,作者提出了一种概率关系矩阵分解模型.该模型的创新点在于不再仅仅只考虑用户的社交关系,而通过学习用户的依赖提高了推荐准确度,但是该方法缺乏对时间上下文和地理上下文的研究.

文献[10]为了解决下一个兴趣点的推荐问题,提出了一种两步策略的方法:首先,基于用户签到的兴趣点种类构建三维张量,并提出一种新的优化准则(LBPR)对张量优化学习,进而得到预测的兴趣点种类;然后,根据预测的兴趣点种类获得位置列表.该方法的推荐效果要优于目前存在的方法,但是该方法没有考虑时间上下文的影响,也缺乏对其他元数据信息的研究,例如用户信息或者兴趣点信息等.

文献[11]认为,用户的兴趣点会随着时间和当前位置的变化而变化,因此,作者提出了两步策略的方法进行兴趣点的推荐:首先,根据用户签到的兴趣点种类和时间上下文构建四维张量,预测用户偏好的下一个兴趣点种类;然后,基于预测的兴趣点种类进一步获得位置列表.该模型的创新点在于既考虑了时间和位置,还降低了数据稀疏性的影响,但是缺乏对其他元数据信息的研究.

为了同时考虑多种数据信息,并进行有效的融合,本文提出了一种融合多种数据信息的餐馆推荐模型(a restaurant recommendation model with multiple information fusion,简称RRMIF).该模型首先利用签到信息和时间上下文构建“用户-餐馆-时间片”的三维张量,同时,利用其他数据信息挖掘若干用户相似关系矩阵和餐馆相似关系矩阵;然后,在概率张量分解模型[12]的基础上同时对这些关系矩阵进行分解,并保证张量和矩阵分解后有共同的低维隐式因子矩阵;最后,利用BPR[13,14]优化准则和梯度下降算法进行模型求解.可以看出,该模型将多种数据信息通过用户、餐馆以及时间片的隐式因子矩阵进行了有效地融合,这也就是本文提出的模型与目前存在的模型最大的区别.值得注意的是,为了降低模型的复杂度,本文提出的模型没有考虑用户的显式反馈.本文的贡献主要包括以下几点.

1)与现有研究不同,本文没有简单地将时间上下文按照小时制划分为24 个时间片,而通过K-means 聚类算法[15]将一天分为4 个用餐时间段,这样不仅对用户的用餐行为进行了聚类,还降低了模型的复杂度;

2)本文基于地理上下文、餐馆属性信息构建了两种餐馆相似关系矩阵,基于用户人口统计信息构建了用户相似关系矩阵;进而提出一种融合多种数据信息的餐馆推荐模型,该模型是在概率张量分解模型的基础上同时对用户相似关系和餐馆相似关系进行分解,它以用户和餐馆的隐式因子作为桥梁,更好地融入了多种数据信息;最后,采用BPR 优化准则和梯度下降算法进行模型求解;

3)实验在两种真实的数据集上进行,主要包括以下4 个部分:1)比较本文提出的模型和现有模型的推荐效果;2)研究多种数据信息对于推荐效果的影响,包括时间上下文、地理上下文、餐馆属性信息以及用户人口统计信息;3)研究本文提出的模型在不同稀疏度数据集的表现,并与现有模型作比较;4)研究本文提出的模型的运行时间,并与现有模型作比较.实验结果表明:相比于目前存在的餐馆推荐模型,本文提出的餐馆推荐模型有着更好的推荐效果和可接受的运行时间,并且缓解了数据稀疏性对推荐效果的影响.

本文第1 节介绍餐馆推荐的相关工作,包括兴趣点推荐和餐馆推荐.第2 节介绍多种数据信息的研究,提出一种融合多种数据信息的餐馆推荐模型.第3 节介绍实验的相关设置及实验结果分析.第4 节是全文的总结.

1 相关工作

1.1 兴趣点推荐

兴趣点推荐[16]作为位置社交网络的一个重要应用,已经成为学术界和工业界的一个热门课题.它给用户和商家都带来了前所未有的便利和好处:对于用户而言,兴趣点推荐系统能够将其从海量的兴趣点搜索中解放出来,根据他们的历史数据挖掘其个性化偏好,为他们推荐合适的兴趣点;另一方面,对于商家而言,可以吸引大量感兴趣的用户,持续提高经济效益.

用户隐式反馈的研究是当前兴趣点推荐的一个热点,矩阵分解模型(MF)[17]就常常被用于隐式反馈数据的处理.该模型基于用户的历史签到数据构建“用户-兴趣点”的签到矩阵,再通过对签到矩阵的分解,得到用户隐式因子矩阵和兴趣点隐式因子矩阵,再利用这些隐式因子矩阵预测用户对于兴趣点的评分,进而为用户生成推荐列表.虽然该模型有着较高的准确率,且模型简单,但是隐式反馈中只有正反馈,当用户在某兴趣点没有签到时,并不能反映用户就不喜欢该兴趣点,传统的矩阵分解没有很好地解决在这一问题.为了从隐式反馈中获得额外的信息,Hu 等人[18]提出了加权矩阵分解模型,该模型在概率矩阵分解的基础上,通过分析用户的隐式反馈,得到正反馈和负反馈的置信水平,从而使得矩阵分解模型更好地应用于隐式反馈的研究.但是由于“用户-兴趣点”矩阵的稀疏性,该方法依旧面临着很大的挑战.为了解决稀疏性问题,Lian 等人[8]提出了结合地理上下文的矩阵分解模型(GeoMF).该模型在加权矩阵分解的基础上将地理上下文引入模型,让用户的活动区域向量融合到用户隐式空间中,将兴趣点的区域影响向量融合到兴趣点隐式空间中.通过这种融合,不仅考虑了用户行为的空间聚类现象,还有效地解决了矩阵稀疏性问题.但是该模型仅仅只考虑了用户的签到信息和地理上下文,而没有考虑用户的评论信息以及时间上下文信息.为了融合用户的评论信息,Li 等人[19]提出了一种多方面考虑的兴趣点推荐系统.该系统从用户对于兴趣点的评论中学习用户的偏好以及商家的质量标签,再结合用户评分矩阵分解得到的用户特征矩阵和商家特征矩阵,预测目标用户对于其他兴趣点的效用评分,最后生成推荐列表.该系统很好地结合了用户的评论信息和评分信息,提高了推荐的精度.但是该系统没有考虑到时间上下文信息.考虑到时间信息对于兴趣点推荐重要性,Luan 等人[20]提出了基于张量分解的协同过滤模型.该模型利用用户的签到行为构建一个“用户-兴趣点-时间片”的三维张量,同时从不同角度提取3 个特征矩阵,例如“用户-兴趣点类别”或者“时间片-用户”等特征矩阵,然后利用特征矩阵协同地对张量进行分解,并使得目标函数最小,最后得到预测张量,通过预测张量就可以为目标用户在某一时间对生成兴趣点推荐列表.虽然该模型考虑了时间因素,提高了推荐准确度,但是该模型没有考虑地理上下文.

1.2 餐馆推荐

目前,国内对于餐馆推荐研究得不多,而国外则相对较多.例如,Fu 等人[21]提出了一种考虑多种评分数据,并融合地理上下文以及用户和餐馆特征信息的餐馆推荐模型.该模型同时对多种评分矩阵进行分解,并利用用户和餐馆的位置信息构建位置相关性,利用用户和餐馆特征信息构建特征相关性,最后利用分解得到的隐式因子矩阵和这两种相关性得到用户对餐馆的预测评分.由于融合了多种评分数据,该模型提高了推荐准确度,但是该模型没有考虑时间上下文信息.为了融入时间上下文,Zhang 等人[6]提出了一种隐式反馈模型.该模型分别从用户签到信息、时间上下文以及其他数据信息获得两种偏好:(1)构建“用户-餐馆-时间片”的三维签到张量,利用概率张量分解从签到张量中获得隐式空间的偏好;(2)利用逻辑回归的方法分析用户依赖于其他数据信息的偏好.最后,结合这两种偏好得到用户在某一时间片对餐馆的预测评分,进而为目标用户在某一时间片生成餐馆推荐列表.该模型虽然同时考虑了多种数据信息,但是该模型是针对各种数据信息分别建模,没有完全挖掘这些数据信息的价值.除了考虑以上数据信息,Sun 等人[7]还考虑了用户的社交网络信息,提出了一种考虑多源信息的餐馆推荐模型.该模型的基本思想是:用户的隐式偏好不仅由用户的评分信息决定,还会受用户社交网络以及行为模式相似人群的影响.因此,作者在矩阵分解的框架中融入了评分信息、社交网络信息以及行为模式信息.该模型虽然有着较高的推荐精度,但是没有考虑餐馆的属性信息.

通过对餐馆推荐相关工作的分析,本文借鉴前人的经验,提出了一种融合多种数据信息的餐馆推荐模型.该模型综合考虑了用户的签到信息、时间上下文、地理上下文、餐馆属性信息以及用户人口统计信息,并有效地将这些信息进行融合,从而进一步提高了推荐精度.

2 融合多种数据信息的餐馆推荐模型

本节首先基于大众点评数据集(相关介绍见第3.1 节)介绍了各种数据信息的研究,通过K-means 算法将一天24 小时划分为4 个用餐时间段,另外,基于地理上下文、基于餐馆属性信息构建两种餐馆相似关系,基于用户人口统计信息构建用户相似关系;然后提出了一种融合多种数据信息的餐馆推荐模型;最后,利用BPR 优化准则和梯度下降算法进行模型求解.

2.1 多种数据信息的研究

2.1.1 时间上下文

文献[6,22]指出:用户在不同时间片对于餐馆的选择是不同的,通过引入时间上下文,可以为目标用户在不同时间片生成相对应的餐馆推荐列表.因此,该文献按照小时制将一天划分成24 个时间片,但是这种方法存在一定的缺点,即需要在每个时间片生成推荐列表,这会导致模型复杂度增大,运行时间变长.实际上,用户的用餐时间是存在聚类现象的,从图1 可以看出:用户的聚餐时间存在明显的高峰和低谷,且高峰段大概有4 段,因此,推荐系统只需要在每个用餐高峰之前为用户生成推荐列表.这样不仅可以降低模型的复杂度,还能保证模型具有较好的推荐效果.

Fig.1 Number of diners at different time slots图1 用户在不同时间片的用餐人数

为了更精确地划分用户高峰,本文利用K-means 算法对数据集的用餐时间进行聚类分析,将用户的用餐时间段分成4 段,聚类结果见表1.

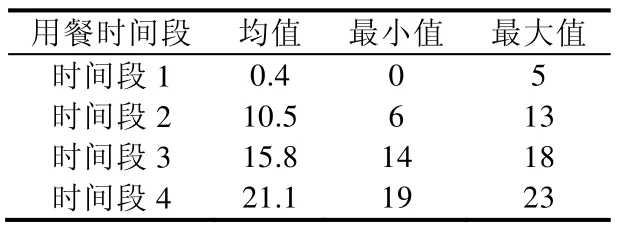
Table 1 Clustering of dining time表1 用餐时间的聚类

从表1 可以看出,通过聚类将一天划分为了4 个用餐时间段,每一段分别对应[0,5],[6,13],[14,18],[19,23].

2.1.2 地理上下文

在目前的兴趣点推荐和餐馆推荐的研究中,地理位置基本都被看做一种影响用户选择的重要因素.对于餐馆而言,用户通常会选择活动区域内的餐馆,那么活动区域内的餐馆之间理应具有相似性.文献[23,24]认为,距离用户100km 以内的区域可以看做是用户的活动区域,那么就可以近似认为餐馆R与距离该餐馆100km 以内的其他餐馆相似,它们之间的相似表现为:用户如果选择了餐馆R,那么该用户也有可能选择距离餐馆R100km 以内的其他餐馆.因此,基于地理位置的餐馆相似关系A可以定义为公式(1):

其中,|loc(i)-loc(j)|表示餐馆i和餐馆j的距离.

2.1.3 餐馆属性信息

餐馆的属性信息包括餐馆的名字、餐馆的风格以及餐馆的平均消费等,为了研究餐馆的风格与用户偏好的关系,我们随机抽取了3 名用户,计算了每个用户选择各种餐馆风格的次数,如图2 所示.需要注意的是,这里的餐馆风格只是所有风格的一部分.

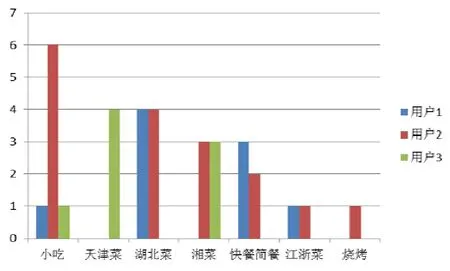
Fig.2 Number of selected times for different restaurant styles图2 用户选择不同餐馆风格的次数

从图2 可以看出,用户通常会多次选择自己喜好的某类餐馆用餐.因此,餐馆风格相同的餐馆理应具有相似性.这种相似性表现为:当用户选择了餐馆R,那么该用户也可能喜欢与餐馆R风格相同的其他餐馆.因此,基于餐馆风格的餐馆相似关系B可以定义为公式(2):

其中,style(i)表示餐馆i的风格.

除了餐馆的风格,餐馆的属性还包括餐馆的平均消费,但是由于很多餐馆的签到次数少,且用户通常很少标注消费金额,导致很多餐馆的平均消费为0.经统计,数据集中平均消费为0 的餐馆占45.1%,因此很难利用餐馆的平均消费进行研究.

2.1.4 用户人口统计信息

用户的人口统计信息一般包括用户的性别、年龄以及居住地,但是由于用户的隐私保护,有的数据很难获取.通过分析用户历史签到的餐馆的所在城市,可以将用户签到次数最多的城市看作是用户的居住地.文献[6]也分析了同一居住地的用户通常会有相似的偏好,例如北京人更偏爱北京菜,湖南人更爱湖南菜.因此,可以得到基于居住地的用户相似关系E,如公式(3)所示:

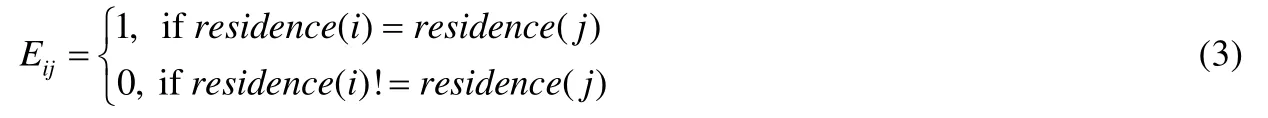
其中,residence(i)表示用户的居住地.

2.2 模型描述

为了更好地融合用户签到信息、时间上下文、地理上下文、餐馆属性信息以及用户人口统计信息,提高推荐精度,本文提出了一种融合多种数据信息的餐馆推荐模型,如图3 所示,其中,

·I,J,S分别表示用户、餐馆以及时间片的个数;

·A,B,C,E是可观察量,其中:A表示基于地理位置的餐馆相似关系,B表示基于餐馆风格的餐馆相似关系,C表示用户的签到张量,E表示基于居住地的用户相似关系;

·Eiv表示用户i与用户v的居住地的相似性,Ajq,Bjp类似.

Fig.3 Graphical representation for a restaurant recommendation model with multiple information fusion图3 一种融合多种数据信息的餐馆推荐模型的图表示

关于用户签到张量C的构建及其含义,在下文会有介绍.另外,表2 介绍了模型参数的符号及其定义.

Table 2 Symbols and definition of model parameters表2 模型参数的符号及定义

2.2.1 融合用户签到信息和时间上下文

根据用户的签到信息和时间上下文,可以构建“用户-餐馆-时间片”的三维签到张量C∈{0,1}I×J×S,其中,I,J,S分别表示用户、餐馆以及时间片的个数,且通过第2.1.1 节的分析,时间片的个数设定为4.如果在时间片s,用户i在餐馆j用餐,则Cijs=1,这代表了用户的正反馈;如果在时间片s,用户i在餐馆j没有用餐,则Cijs=0,这并不一定代表用户的负反馈,因为用户i可能并不知道餐馆j.从图3 可以看出,通过对三维签到张量C的分解,可以得到用户、餐馆和时间片的隐式因子矩阵,分别用UI×D,VJ×D,TS×D表示,即:每一个张量元素Cijs都可以分解为用户i、餐馆j以及时间片s的隐式特征向量,分别表示为Ui,Vj,Ts.

2.2.2 融合其他数据信息

文献[24]认为用户的社交关系影响了用户行为,因此同时分解社交网络矩阵和评分矩阵,且分解后有一个共同的用户隐式因子矩阵.基于此思想,我们认为:用户i的相似用户影响了用户i的特征向量,餐馆j的相似餐馆也影响了餐馆j的特征向量.因此,本文同时分解基于居住地的用户相似关系E、基于地理位置的餐馆相似关系A、基于餐馆风格的餐馆相似关系B和用户签到张量C.从图3 中可以看出,矩阵E分解为UI×D和FI×D,其中,UI×D是矩阵E和张量C分解后的共同隐式因子矩阵;矩阵A分解为VJ×D和ZJ×D,矩阵B分解为VJ×D和MJ×D,其中,VJ×D是矩阵A,B以及张量C分解后的共同隐式因子矩阵.

2.2.3 模型的基本原理

在概率张量分解模型[12]的研究中,隐式特征向量是由多元高斯分布生成的,而张量的每个元素是由高斯分布生成的,且该分布的均值是由相应的隐式因子决定的.由于本文提出的模型是在概率张量分解模型基础上的扩展,因此该模型的基本原理可以描述如下.

4.对于基于居住地的用户相似关系E中的每个元素,其中,表示Eiv是由均值为Ui·Fv、方差为的高斯分布生成的;

5.对于基于地理位置的餐馆相似关系A中的每个元素;

6.对于基于餐馆风格的餐馆相似关系B中的每个元素Bjq,,其中,;

7.对于三维签到张量C中的每个元素Cijs,,其中,.

2.3 模型参数求解

无论是张量分解还是矩阵分解,都是通过分解得到的低维隐式因子矩阵来求得预测张量或者预测矩阵,并使得预测张量和原始张量的误差最小,使得预测矩阵和原始矩阵的误差也最小.因此,该模型的目标函数可以定义为公式(4):

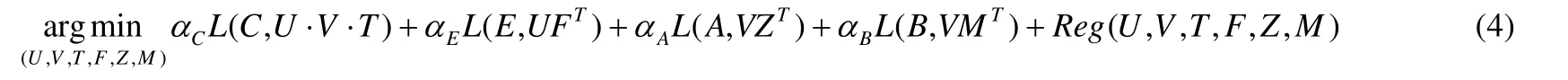
其中:L是误差函数;Reg是防止过拟合的正则项;αC,αE,αA,αB分别是各个误差项的比重,且αC+αE+αA+αB=1;U·V·T表示预测张量,其中,预测张量的每一项.

由于用户的相似关系矩阵E是对称矩阵,则U=F;同理,V=Z=M.那么,该模型的目标函数可以简化为公式(5):

文献[13,14]认为:推荐列表的生成实际上是一种排名问题,通过优化项目的排名,可以优化目标函数,使得模型更快地收敛到最优解.因此,该文献通过BPR 优化准则和梯度下降算法进行求解.实验表明,直接优化排名的方法要明显优于其他方法.受此启发,本文使用BPR 优化准则来优化误差函数.

BPR 优化准则的基本思想是:当Cijs=1,Cij′s=0 时,用户i在时间片s对于餐馆j的排名要高于餐馆j′.对于签到张量C,定义一个集合PC来表示C中的排名对,如公式(6)所示:

对于L(c,U·V·T)的优化,可以转化为公式(7):

对于其他误差函数的优化,同样采用BRP 优化准则,分别如公式(8)～公式(10)所示:

其中,

对于正则项Reg(U,V,T),为了方便使用梯度下降算法[25]进行求解,本文采用L2-regularization[26],如公式(11)所示:

其中,λU,λV和λT是正则化参数,都是L2范数的平方.

综上,该模型的目标函数可以转化为公式(12):

利用梯度下降算法最大化这个目标函数,就可以得到模型参数U,V,T.需要注意的是,由于是最大化目标函数,因此必须沿着梯度方向迭代,而不是负梯度方向.对于模型参数的完整求解过程见算法1.

算法1.求解模型参数.

输入:用户的签到张量C,基于居住地的用户相似关系E,基于地理位置的餐馆相似关系A,基于餐馆风格和消费的餐馆相似关系B,方差参数σU,σV,σT,误差权重αC,αE,αA,αB,正则化参数λU,λV,λT,迭代次数Iter,学习速率参数uC,uE,uA,uB,隐式因子个数D;

输出:模型参数U,V,T.

从算法1 可以看出,模型求解的时间复杂度为O(Iter×(|PC|+|PE|+|PA|+|PB|)×D),其中:Iter为迭代次数;|PC|,|PE|,|PA|和|PB|分别表示集合PC,PE,PA和PB中元素的个数,即排名对的个数;D表示隐性因子的个数.通过学习到的模型参数U,V,T,就可以得到预测签到张量ˆC,从而为目标用户在某一时间片生成餐馆推荐列表.

3 实验及结果分析

3.1 数据集及实验环境

本文使用大众点评数据集(http://yongfeng.me/)和Yelp 数据集(https://www.yelp.com/dataset)进行餐馆推荐研究.这两种数据集都包括用户的评论数据集和商家的属性数据集,由于用户隐式的保护,都没有公开用户的人口统计信息.用户的评论数据集中都包括用户的评分、评论以及消费信息,不同的是:Yelp 数据集给出的评论时间只具体到哪一天,而大众点评数据集具体到了一天中的某个时刻.另外,本文将用户评论一次可以看做签到一次.商家的属性数据集都包括商家的ID、名字、位置(城市、经纬度等)、餐馆的种类以及标签等信息.

在这两种数据集中,商家不仅包括餐馆,还包括超市、酒吧以及茶馆等.由于除了餐馆的其他商家与研究的主题无关,因此首先必须从数据集中剔除与餐馆无关的信息.对处理后的两种数据集,各项统计信息见表3.

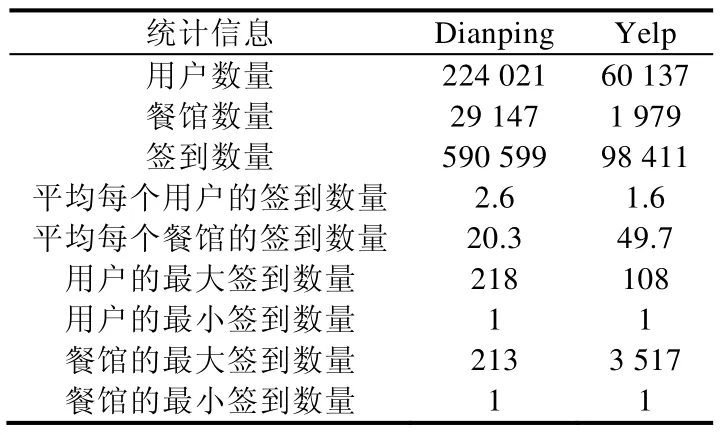
Table 3 Statistics of dataset表3 数据集的各项统计信息

从表3 中可以看出,Yelp 数据集中,用户的数量是Dianping 数据集中用户数量的将近3 倍;而Dianping 数据集中,餐馆的数量是Yelp 数据集中餐馆数量的近15 倍.这可能导致模型在Yelp 数据集中的推荐效果要优于Dianping 数据集.

为了更好地验证推荐模型的效果,分别将两种数据集划分为训练集(80%)和测试集(20%),训练集主要是用来学习推荐模型中的参数,测试集主要是用来验证模型的推荐效果.

本文的实验环境为:Windows7 操作系统,4GB 内存,Intel(R)Core(TM)2 Duo CPU 2.93GHz,实验程序使用java1.6 语言开发.

3.2 评价指标

对于基于隐式反馈的推荐而言,MAE 不是一个很好的评价指标,因为与评分不同,隐式反馈只有1 或者0,而且由于数据的稀疏性,1 的数目会很少,这样,计算MAE 是没有意义的.因此,为了验证推荐的效果,本文采用recall@K作为评价指标,对于recall@K的定义如公式(13):

其中,recall@K表示在top-K列表中的召回率;hit表示测试集中的命中次数,所谓命中是指如果测试集中的签到餐馆出现在了top-K的推荐列表中,那么就表示命中一次;recall表示测试集签到总次数.

3.3 实验结果与分析

在这一节,主要在两种数据集中分别进行以下实验:(1)比较本文提出的模型(RRMIF 模型)和现有模型的推荐效果;(2)研究多种数据信息对于推荐效果的影响,包括时间上下文、地理上下文、餐馆风格以及用户居住地;(3)研究RRMIF 模型在不同稀疏度数据子集的表现,并与现有模型作比较;(4)研究RRMIF 模型的运行时间,并与现有模型作比较.

通过网格搜索法对RRMIF 模型的参数进行调优,得到实验效果最好的模型参数如下:方差参数σU=σV=σT=0.1;正则化参数λU=λV=λT=0.004;误差参数αC=0.45,αE=0.2,αA=0.3,αB=0.05;迭代次数Iter=40;学习速率参数uC=0.2,uE=0.06,uA=0.1,uB=0.04 以及隐性因子个数D=10.

值得注意的是:由于Yelp 数据集中没有提供用户在一天中具体的签到时间,因此时间片的大小为1;而对于Dianping 数据集,按照上文的聚类结果,将时间片的大小设置为4.

3.3.1 与其他对比模型的比较

为了验证文中提出的RRMIF 模型的推荐效果,本文选取下面几种利用用户隐式反馈来进行兴趣点推荐的相关模型作为对比.

(1)概率矩阵分解模型(PMF)[17]:该模型主要是利用了用户的签到信息,将“用户-兴趣点”的签到矩阵分解为用户隐式因子矩阵和兴趣点隐式因子矩阵,再利用这些隐式因子矩阵预测用户对于兴趣点的评分,进而为用户生成推荐列表;

(2)加权矩阵分解模型(WMF)[18]:该模型在概率矩阵分解的基础上,通过分析用户的隐式反馈,得到正反馈和负反馈的置信水平,从而使得矩阵分解模型更好地应用于隐式反馈的研究;

(3)基于用户的协同过滤模型(UCF)[27]:该模型主要利用相似度计算目标用户的相似用户集合,然后根据相似用户对于目标项目的评分预测目标用户对目标项目的评分,最后给出推荐列表;

(4)结合地理位置信息的矩阵分解模型(GeoMF)[8]:该模型在加权矩阵分解的基础上引入了地理上下文,将用户的活动区域向量融合到用户隐式空间中,将兴趣点的区域影响向量融合到兴趣点隐式空间中.通过这种融合,不仅考虑了用户行为的空间聚类现象,还有效地解决了矩阵稀疏性问题;

(5)隐式反馈模型(IPM)[6]:该模型首先构建“用户-餐馆-时间片”的三维签到张量,利用概率张量分解从签到张量中获得隐式空间的偏好;其次,利用逻辑回归的方法分析用户依赖于其他数据信息(餐馆属性、用户人口统计信息)的偏好;最后,结合这两种偏好得到用户在某一时间片对餐馆的预测评分,进而为目标用户在某一时间片生成餐馆推荐列表.

该实验设置top-K=5,10,15,20,25,30,且当上述5 种模型的参数设置为最优参数时,比较各模型在Dianping数据集和Yelp 数据集中的召回率(recall@K),结果如图4 所示.

Fig.4 recall@K comparison of different model图4 不同模型的召回率比较

观察图4 可以得到以下结果.

(1)无论在哪种数据集中,PMF 模型的推荐效果都是最差的,这主要是因为用户的签到数据是稀疏的;另外,PMF 模型没有考虑时间上下文,也没有融合其他数据信息;

(2)在两种数据集中,WMF 模型的推荐效果都要优于PMF 模型.这是因为WMF 模型在PMF 模型的基础上还分析了正负反馈的置信水平,从而提升了推荐效果;

(3)在两种数据集中,UCF 模型的推荐效果都要明显优于WMF 模型和PMF 模型.但是UCF 模型存在以下缺点:面对大数据集,模型的复杂度会急剧增大;很难融入其他数据信息,不易扩展.而对于WMF 模型和PMF 模型,则更易扩展,且面对大数据集仍然表现不错.因此,WMF 模型和PMF 模型在适用性上要强于UCF 模型;

(4)与WMF 模型相比,在两种数据集中,GeoMF 模型的推荐效果都要明显优于WMF 模型.这主要是因为GeoMF 模型考虑了餐馆的地理位置信息,从而缓解了数据的稀疏性问题,也提高了推荐效果;

(5)在两种数据集中,IPM 模型的推荐效果都要明显优于GeoMF 模型、WMF 模型、UCF 模型和PMF 模型.这是因为IPM 模型考虑了餐馆的地理位置信息,并融入了时间上下文和其他数据信息;

(6)在两种数据集中,RRMIF 模型的推荐效果都是最好的.这充分地说明了,虽然IPM 模型和RRMIF 模型都考虑了多种数据信息,但是RRMIF 模型相比于IPM 模型更加有效地将多种数据信息进行融合,充分挖掘了多种数据信息的价值,从而提升了推荐效果;

(7)Yelp 数据集中,各模型的召回率趋势相比于Dianping 数据集更加紧凑,而且各模型在Yelp 数据集中的推荐效果要明显优于Dianping 数据集.这主要是因为Yelp 数据集中餐馆的数量要明显少于Dianping数据集,导致各模型的差距相对缩小.

实验结果表明:RRMIF 模型相比于现有模型,更加有效地融合了多种数据信息,提升了推荐效果.

3.3.2 多种数据信息对推荐效果的影响

为了研究多种数据信息对于推荐效果的影响,该实验对下面9 种推荐模型进行对比.

(1)概率矩阵分解模型(PMF):该模型仅仅考虑用户的签到信息,而没有考虑时间上下文、地理上下文以及其他数据信息;

(2)概率张量分解模型(PTF)[12]:该模型仅仅考虑用户的签到信息和时间上下文,对用户签到张量进行分解,而不考虑地理上下文和其他数据信息;

(3)PTF+E:该模型不仅考虑用户的签到信息和时间上下文,还考虑了基于居住地的用户相似关系E,同时对签到张量和关系矩阵E进行分解;

(4)PTF+A:该模型不仅考虑用户的签到信息和时间上下文,还考虑了基于地理位置的餐馆相似关系A,同时对签到张量和关系矩阵A进行分解;

(5)PTF+B:该模型不仅考虑用户的签到信息和时间上下文,还考虑了基于餐馆风格的餐馆相似关系B,同时对签到张量和关系矩阵B进行分解;

(6)PTF+E+A:该模型不仅考虑用户的签到信息和时间上下文,还考虑了基于居住地的用户相似关系E和基于地理位置的餐馆相似关系A,同时对签到张量、关系矩阵E和关系矩阵A进行分解;

(7)PTF+E+B:该模型不仅考虑用户的签到信息和时间上下文,还考虑了基于居住地的用户相似关系E和基于餐馆风格的餐馆相似关系B,同时对签到张量、关系矩阵E和关系矩阵B进行分解;

(8)PTF+A+B:该模型不仅考虑用户的签到信息和时间上下文,还考虑了基于地理位置的餐馆相似关系A和基于餐馆风格的餐馆相似关系B,同时对签到张量、关系矩阵A和关系矩阵B进行分解;

(9)PTF+A+B+E(RRMIF):该模型就是本文提出的RRMIF 模型,它不仅考虑用户的签到信息和时间上下文,还考虑了基于居住地的用户相似关系E、基于地理位置的餐馆相似关系A以及基于餐馆风格的餐馆相似关系B,同时对签到张量、关系矩阵E、关系矩阵A和关系矩阵B进行分解.

该实验设置top-K=5,10,15,20,30,且当上述9 种模型的参数设置为最优参数时,比较各种模型在两种数据集中的召回率(recall@K),如图5 所示.

Fig.5 Research of multiple data information图5 多种数据信息的研究

从图5 中可以看出:

(1)在Dianping 数据集中,PMF 模型的推荐效果要低于PTF 模型,这主要是因为PTF 模型考虑了时间上下文信息;而在Yelp 数据集中,PMF 模型的推荐效果几乎与PTF 模型一样,这主要是因为Yelp 数据集中没有用户签到的具体时间,因此时间片设置为1,因此,PTF 模型的效果基本和PMF 模型相同;

(2)在两种数据集中,PTF+A>PTF+E>PTF+B>PTF.这验证多种数据信息对于用户餐馆选择的影响,并且餐馆的地理位置影响最大,其次是用户的居住地,最后是餐馆的风格;

(3)在两种数据集中,PTF+A+E>PTF+A+B>PTF+B+E.这说明如果只考虑两种数据信息,同时考虑餐馆地理位置和用户居住地的效果是最好的;

(4)在两种数据集中,PTF+A>PTF+B+E.这说明考虑餐馆的地理位置对于推荐效果的提升比同时考虑用户的居住地和餐馆风格还要大;

(5)无论在哪种数据集中,PTF+A+B+E 的推荐效果都是最好的,这个模型也就是本文提出RRMIF 模型.这说明当同时考虑了餐馆的地理位置、餐馆的风格以及用户的居住地时,模型的效果是最好的;

(6)Yelp 数据集中,各模型的召回率要相比于Dianping 数据集更紧凑.这是由于数据集本身特性的影响,Yelp 数据集中餐馆的数量明显少于Dianping 数据集.

实验结果表明,多种数据信息能够有效地提高推荐的效果,按照作用大小排序如下:餐馆地理位置>用户居住地>餐馆风格;另外,RRMIF 模型通过融合多种数据信息,使得推荐效果明显要优于只融合一种或者两种数据信息的模型.

3.3.3 稀疏性验证

为了验证RRMIF 模型在不同稀疏度数据集的表现,该实验从Dianping 数据集和Yelp 数据集中分别抽取了4 种稀疏度不同的数据子集,各数据子集的统计信息见表4.其中,稀疏度定义为

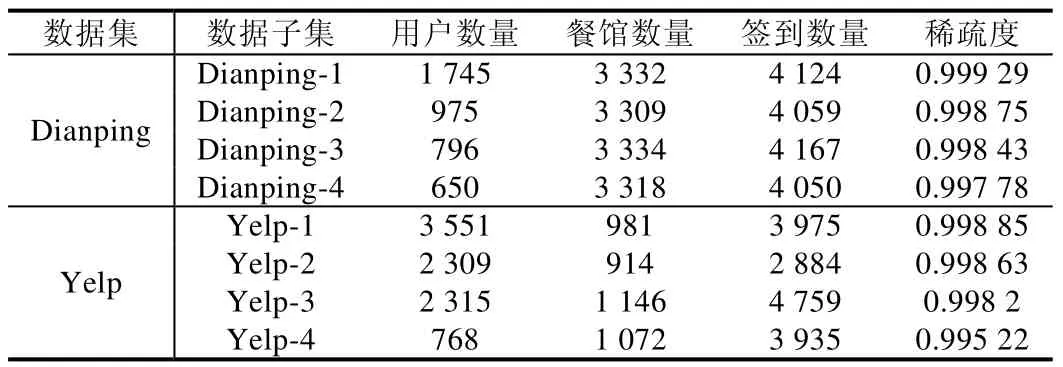
Table 4 Statistics of different sparse subset表4 不同稀疏度数据子集的统计信息

从表4 中可以看出,按照稀疏度排序:

RRMIF 模型与第3.3.1 节中的5 种对比模型在以上各数据子集的召回率(recall@30)比较如图6 所示,从图6 中可以看出:

(1)随着数据稀疏度的降低,PMF 模型的推荐效果逐渐提升.例如,PMF 模型在Dianping-3 的效果相比于Dianping-1 提升了1.5 倍,相比于Dianping-2 提升了35%.这是因为PMF 模型的目的是通过矩阵中的“1”来填充整个矩阵的值,因此极易受数据的稀疏性影响.当数据相对稠密时,也就是说矩阵中“1”的比例相对较多时,模型的效果就会得到提升.另外,PMF 模型在Dianping-4 的效果相比于Dianping-3 降低了2.3%.这说明PMF 模型随着数据稀疏度的继续增加,PMF 模型的推荐效果会逐渐趋于平稳,并有降低的趋势;

(2)与PMF 模型类似,UCF 模型和WMF 模型随着数据稀疏度的降低,推荐效果都有明显的提升,且最后也会趋于平稳.WMF 模型通过引入正负反馈的置信水平来提升推荐效果,但是正负反馈的置信水平仍然受到数据稀疏性的影响.UCF 模型是通过用户的共同评分来计算用户相似度的,因此数据的稀疏性影响着UCF 模型的推荐效果;

(3)从Dianping 的数据子集中可以看出,随着数据稀疏度的变化,GeoMF 模型推荐效果变化不大.这是因为该模型考虑了餐馆的地理位置信息,缓解了矩阵的稀疏性问题;

(4)在Dianping 的数据子集中,随着数据集稀疏度的变化,IPM 模型的推荐效果相对稳定;而在Yelp 数据子集中,IPM 模型的推荐效果还是受到了稀疏性的影响;

(5)不论在Dianping 的数据子集还是在Yelp 的数据子集,RRMIF 模型的推荐效果都是最好的,而且基本不受数据稀疏性的影响.这说明本文提出的模型不仅在有效性上优于其他对比模型,在稳定性上也要优于其他对比模型;

(6)随着数据稀疏度的降低,其他对比模型的推荐效果有一定的提升,但仍然低于RRMIF 模型.

Fig.6 Sparsity verification图6 稀疏性验证

实验结果表明:相比于现有其他模型,RRMIF 模型在数据极其稀疏的情况下仍然能够很好地进行推荐,这说明RRMIF 模型有效地缓解了数据稀疏性对于推荐效果的影响.

3.3.4 效率评估

在实际应用中,推荐模型的运行时间往往是重要的评价指标之一,如果模型的运行时间超过了可接受范围,那么这个模型的实用性就会受到限制.该实验主要对RRMIF 模型和第3.3.1 节中的5 种对比模型分别在Dianping 数据集和Yelp 数据集进行效率的评估.首先,从Dianping 数据集分别抽取4 种用户数量不同的数据子集,用户数量分别为300、600、1200 和2400,然后得到RRMIF 模型和其他5 种对比模型在4 种数据子集的运行时间.为了全面地进行效率比较,在Yelp 数据集上按照相同的操作进行.最后,分别得到各模型基于两种数据集的效率评估,如图7 所示.横轴表示用户数量,纵轴表示为运行时间,单位为秒(s).

从图7 中可以看出:

(1)在两种数据集中,PMF 模型、WMF 模型、UCF 模型和GeoMF 模型的运行时间大致排序为:GeoMF>UCF>WMF>PMF.这是因为WMF 模型是基于PMF 模型,考虑了正负反馈的置信水平,增加了一个权重矩阵;而GeoMF 模型是基于WMF 模型,考虑餐馆的地理位置信息,增加了特征向量的维数.对于UCF 模型,需要计算每个用户的相似用户,受用户数量影响明显,当用户数量增加时,会出现运行时间陡增的情况;

(2)Dianping 数据集中,模型的运行时间相比于Yelp 数据集显著地增加,这主要有两个原因:第一,因为Yelp 数据集中用户的签到时间没有具体到一天的某个时刻,因此时间片设置为1,这样就导致Yelp 数据集中的模型的运行时间显著地降低;第二,Dianping 数据集的稀疏度要低于Yelp 数据集,这有可能导致了运行时间较高;

(3)无论在Dianping 数据集还是在Yelp 数据集,IPM 模型的运行时间都是最多的.IPM 模型的运行时间是最长的,而且随着数据集的增大,运行时间也随之增长,并且增长速率也逐渐增大,几乎呈现指数增长的趋势.这主要有两方面的原因:第一,该模型对多种数据信息预处理的复杂度相对较高;第二,该模型除了要通过概率张量分解进行求解,还需要通过逻辑回归求解;

(4)基于Dianping 数据集,RRMIF 模型的运行时间要高于GeoMF 模型、WMF 模型、UCF 模型和PMF模型,这主要是因为RRMIF 模型考虑了时间上下文信息,需要为用户在某一时间片生成推荐列表,因此计算的时间复杂度增大.而基于Yelp 数据集,RRMIF 模型的运行时间虽然高于PMF 模型,但是要低于GeoMF 模型、WMF 模型和UCF 模型.这是因为基于Yelp 数据集的实验,时间片设置为1,这样,RRMIF 模型的运行时间显著降低.这也说明了在同样不考虑时间上下文的情况下,RRMIF 模型的运行效率是相当可观的;

(5)从这两种数据集可以看出:RRMIF 模型的运行时间虽然随着数据集的增大而增大,但是没有呈现出急剧增大的趋势.换句话说,该模型的运行时间随着数据集的增大而平稳增大.因此,本文提出的模型在大数据集下仍然是实用的.

Fig.7 Efficiency evaluation of different model图7 各模型的效率评估

实验结果表明,RRMIF 模型的运行时间要远低于IPM 模型,略高于其他模型.但是随着数据量的增大,RRMIF 模型的运行时间几乎呈现稳定增长的趋势.这说明RRMIF 模型的运行时间虽然不是最少的,但是它的增长趋势仍然是可接受的.

4 总结

本文首先介绍了餐馆推荐的相关工作,包括兴趣点推荐和餐馆推荐,并分析了现有推荐模型的优缺点.然后,基于大众点评数据集研究了多种数据信息对于用户餐馆选择的影响,并通过K-means 聚类算法将一天24 小时分为4 个用餐时间段.另外,基于地理上下文、餐馆属性信息构建了两种餐馆相似关系矩阵,基于用户人口统计信息构建了用户相似关系矩阵.在此基础上,本文提出了一种融合多种数据信息的餐馆推荐模型(RRMIF).该模型首先利用签到信息和时间上下文构建“用户-餐馆-时间片”的三维张量;然后,在概率张量分解模型的基础上同时分解用户相似关系矩阵和餐馆相似关系矩阵;最后,利用BPR 优化准则和梯度下降算法进行模型求解.为了更加全面地验证RRMIF 模型的有效性,本文基于大众点评数据集和Yelp 数据集做了以下4 个实验:(1)与现有模型比较;(2)研究多种数据信息对推荐效果的影响;(3)稀疏性验证;(4)效率评估.最后,实验结果表明,相比于目前存在的餐馆推荐模型,RRMIF 模型有着更好的推荐效果和可接受的运行时间,并且缓解了数据稀疏性对推荐效果的影响.