圆形图像抗旋转高效高鉴别特征表示方法*

张东波,陈红磊,文登伟,汤红忠,许海霞

1(湘潭大学 信息工程学院,湖南 湘潭 411105)

2(机器人视觉感知与控制技术国家工程实验室(湖南大学),湖南 长沙 410012)

通讯作者:张东波,E-mail:zhadonbo@163.com

现实生活中存在大量的圆形图像目标识别问题,例如车标、图标、图徽、商标、标签、硬币、装饰物上的圆形花纹和图案等.在很多场合,圆形图像印制、摆放的角度具有随意性,因此图案常出现不同角度的旋转.为了解决现实场景中圆形图像目标的识别,首先要保证在特征提取和图像描述时的抗旋转变换能力,这样才能保证在只获得少量特定角度训练样本前提下实现任意角度圆形图像目标的识别,从而避免搜集和存储大量的各种角度的圆形图像样本.以往的文献中没有专门针对圆形图像目标识别的研究,但是在各种应用案例中有相关的研究报道,例如对硬币图案的识别、车标的识别、LOGO 标签的识别等.

图像目标识别一直是计算机视觉领域的热点研究问题,其通常包括图像预处理、特征提取与描述、分类器设计与学习等环节,其中,特征提取与描述最为关键,需要综合考虑鉴别能力、计算复杂性和鲁棒性等因素.针对圆形图像目标的识别问题,我们希望构建一种具有广泛适用性的抗旋转高效高鉴别的特征提取与描述方法.

图像目标检测与识别的常用特征描述算子分为浮点型和二值型两类:浮点型描述子通常基于梯度计算,通过梯度值和梯度方向信息进行描述,著名的有SIFT[1],SURF[2],MROGH[3],HOG[4]等,其优点是鉴别能力强,但计算量大比较耗时.二值描述算子中有代表性的是LBP[5],BRIEF[6],ORB[7],BRISK[8],FREAK[9]等,二值描述算子通常直接比较图像像素之间灰度大小,优点在于计算简单,计算和匹配效率高,缺点是由于量化信息损失,其鉴别能力较弱.

为了实现抗旋转特征提取和图像描述,需要考虑两个方面的问题:一是在特征计算时应该具有抗旋转变换能力,二是通过池化操作对图像做整体描述时应该具有旋转不变性.方向校正是特征计算和池化操作常用的抗旋转技术手段,SIFT 和SURF 算子通过估计局部主梯度方向作为参考方向,然后做适当的方向校准实现抗旋转变换.但由于梯度方向估计可能存在±20°的误差[10],因此易导致偏差.LBP 为了获得旋转不变特征模式[5],则通过排序策略找到具有最小模式值的模式特征作为代表模式.该处理策略在梯度方向直方图中也可以借用,例如找到最大梯度方向,然后以此为基准,按顺时针或逆时针方向重新排列梯度方向直方图.但是此类方法易受噪声和其他因素干扰,有时难以获得稳定的排序关系.也有研究人员采用成对特征点的梯度方向夹角取代方向,由于夹角和旋转无关,因此可实现旋转不变描述[11].构建局部坐标系统也是在特征计算阶段常用的一种抗旋转变换策略,例如樊彬的局部旋转不变坐标系统[10]、文献[12]采用的径向梯度变换,局部坐标系统在获得旋转不变性能力上,具有严谨的理论支撑,有相对稳定的性能.

在对图像整体描述时的特征池化操作中,通常会采用格状空间划分,但如果不做方向校正的话,格状空间不具备旋转不变性.现有文献中,最典型的旋转不变描述有环状空间划分[13]和基于灰度排序的池化策略[14].

· 环状空间划分原理简单,具有天然的旋转不变性,因此在做旋转不变描述时,其特征表达最为稳定.但由于对图像空间的描述比较粗糙,造成空间信息损失,因此特征鉴别能力不强.这也是很多特征描述方法不采用环状空间划分而往往采用格状空间划分的原因,例如SIFT,HOG 等;

· 灰度排序则通过对灰度区间的量化和排序实现和旋转无关的图像描述,其在实际应用中也有不错的性能表现.但是灰度强度易受照明的影响,此外,该方法对目标遮挡和污渍敏感,因此实际应用中也有较大的局限性.

鉴于上述分析,本文提出一种针对圆形图像目标的抗旋转高效高鉴别特征提取与描述方法.该方法为了解决特征计算的抗旋转能力,采用了径向变换技术,同时,充分利用了圆形图像目标本身呈中心对称的外观特点,采用环状空间特征池化策略,并且利用空间对称区域结构的描述提升了环状空间描述的鉴别能力.此外,由于该方法属于二值模式特征,其继承了传统二值模式特征计算和匹配高效的优点.

1 抗旋转对称结构模式特征提取

1.1 现有LBP模式计算原理及缺陷

局部二值模式(local binary pattern,简称LBP)是一种简单有效的特征提取算法,原LBPp,r是通过比较中心像素和半径为r的圆形邻域的P个像素点的灰度大小来实现微观邻域结构的描述.LBP 具有原理简单、单调照明变化不变性等优点,改进后的LBP 具有旋转不变性,因此广泛应用在图像匹配与图像识别等领域,特别是在纹理分析与人脸识别领域.

为了降低模式数目,可以只保留有重要意义的模式结构,因此,研究人员提出了统一模式,统一模式在一次二进制循环计算中只产生两次变化.为了实现旋转不变性,Ojala 等人[5]又提出了旋转不变LBP,通过旋转圆形邻域可以得到一系列初始定义LBP 值,取其中最小值作为该邻域LBP 值,旋转不变模式记作.结合统一和旋转不变模式原理,可以得到旋转不变统一模式.以邻域p=8 为例,其模式数目从最初的28=256 种减少到10 种.由于兼具统一模式和旋转不变模式的特点,在图像识别领域得到广泛应用,特别是在需要提取旋转不变特征的场合.旋转不变统一二值模式由下式(1)计算:

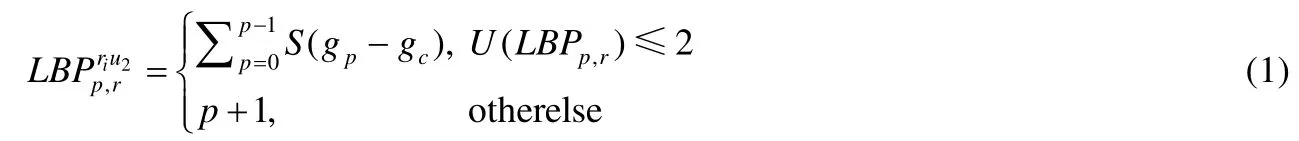
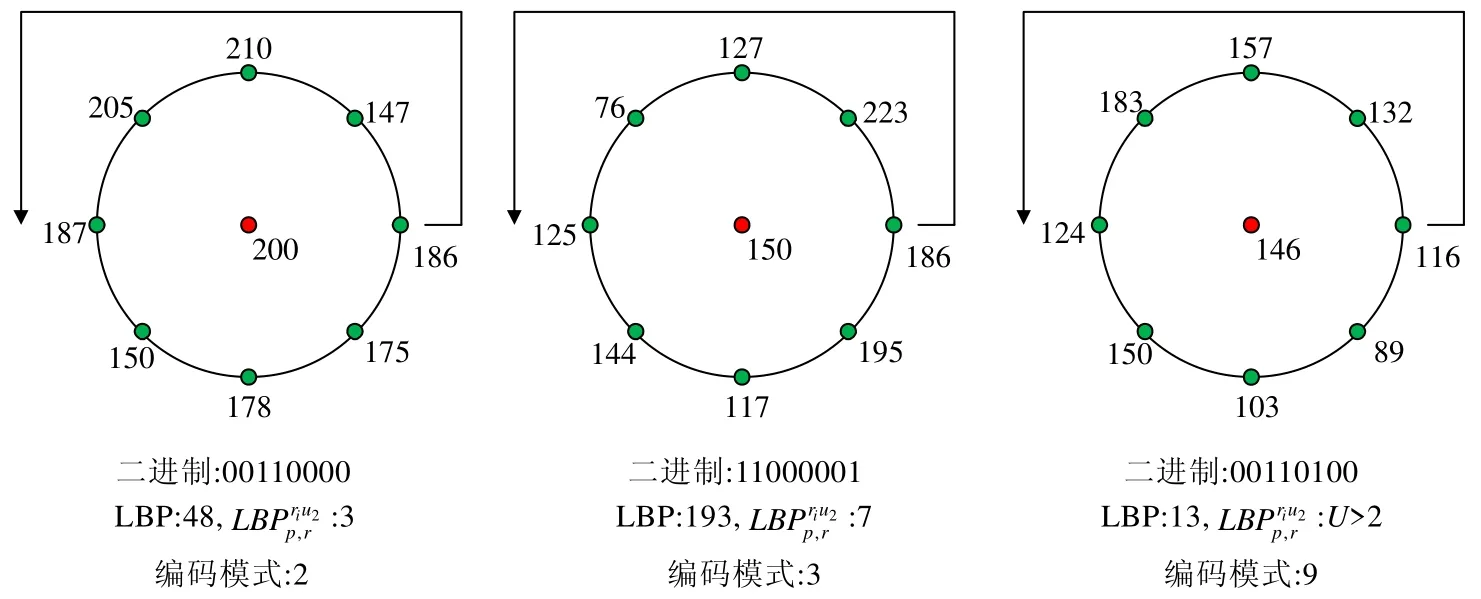
Fig.1 Illustration of the calculation of LBP and 图1 LBP 和计算示例图

考虑到圆形图案的外观特点,在进行图像整体描述时,为了获得旋转不变性,我们很自然地考虑采用环形特征池化操作.但是环形空间划分本身鉴别能力弱,不利于后续识别.如果采用经典的旋转不变统一模式特征,其只能描述10 种结构模式,不利于图像细节的描述,这会影响特征的鉴别能力.因此,为了既能保留环形空间在处理旋转不变描述时的天然优势,同时又能弥补环形空间划分造成的空间信息损失,有必要利用更多的空间结构信息来有效提高特征的鉴别能力.本文充分利用圆形图案中心对称的特点,提出一种基于空间对称位置描述的二值模式特征提取方法.

1.2 基于局部径向坐标变换的旋转不变二值模式及其近似计算

为了获得旋转不变描述,我们引入局部径向坐标变换技术,并按照给定样本点的径向与切向方向选取邻域点进行编码.提取样本点b的旋转不变二值模式原理如图2 所示:c为图像中心,沿cb方向称为径向坐标轴,垂直cb方向称为切向坐标轴,b为新的局部坐标系统原点.分别在径向r和切向t方向找到对称的与p点的距离为d的4 个邻域点,沿逆时针分别记作b1,b2,b3,b4,其中,径向方向上的邻近点为b1,b3,切向方向上的邻近点为b2,b4,然后按照b1,b2,b3,b4的顺序与b点的像素值进行比较,由公式(2)得到二进制数编码T=(T1T2T3T4):

将4 位二进制数T按下式转化为10 进制数,即可得到对应的编码值:

其中,I(b)为b点的像素值,I(bi)为所取点bi的像素值,F为编码值.该二值编码方法可以描述16 种二值模式,与旋转不变统一模式相比,其不仅具有旋转不变性,而且可以表示更多的细节信息.

在构建局部坐标系统时,需要进行浮点数插值计算,这需要大量的计算时间代价.为了避免插值计算,提高计算速度,我们可以采用近似计算,其原理如图3 所示:在圆形区域内,将图像中心径向方向以45°为单位,划分8个扇区,如图3 虚线所分隔扇区.环状空间中采样点的近似编码计算示例如图4～图7 所示.

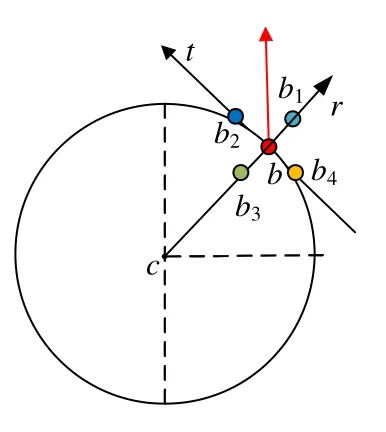
Fig.2 Diagram of local radial coordinate transformation图2 局部径向坐标变换示意图

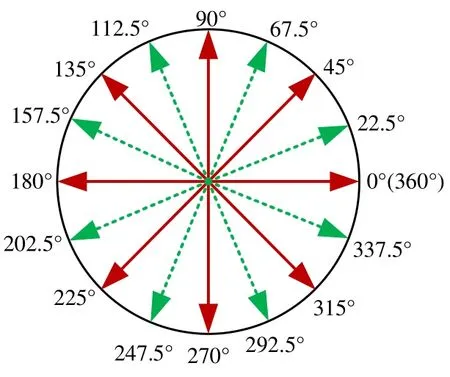
Fig.3 Sector schematic for radial approximate coding图3 径向近似计算的扇区示意图

如图4 所示,假设点A,B,C分别为圆上一点,它们与图像中心夹角分别为θA<22.5°,22.5°<θB<67.5°,67.5°<θC<112.5°,图5～图7 给出了3 个点在3×3 邻域内的近似编码计算实例.此时,点A的编码起始位置b1为邻域水平方向右边像素点,即图5 中像素值为120 的位置,按逆时针方向分别取右、下、左、上这4 个点进行编码.对于点B来说,则编码起始位置b1为邻域右上角像素点,即图6 中像素值为137 的位置,此时按右上、右下、左下、左上的顺序取对角线的4 个点,实现逆时针编码.而点C的编码起始位置b1则为邻域垂直方向上方像素点,即图7中像素值为128 的位置,按上、右、下、左顺序取4 个点实现逆时针编码.点A,B,C编码计算过程示意图分别如图5～图7 所示.

Fig.4 Location of points A,B,C图4 点A,B,C 所在位置图

Fig.5 Encoding calculation process of point A图5 点A 编码计算过程图

Fig.6 Encoding calculation process of point B图6 点B 编码计算过程图

Fig.7 Encoding calculation process of point C图7 点C 编码计算过程图

1.3 环形空间对称结构模式提取

在对圆形物体ROI 区域中的每个点进行编码后,考虑到圆形图案中心对称的特点,我们采用环状空间特征池化策略;同时,为了提升环状空间描述的鉴别能力,我们提出空间对称结构对的方式提取成对点的特征模式.

由于圆形物体的ROI 区域为圆形,因此可将该区域按照等面积的原则划分为若干个交叠的圆环区域,如图8 所示,其中,第m个圆环包含的区域半径为,其中,n为圆环的个数,R为圆形ROI 区域半径.假设(x0,y0)为ROI 圆形区域的中心点,(i,j)为区域内任意一点,(i′,j′)为(i,j)的对称点,则两者之间的坐标关系由公式(4)求得:

分别对(i,j)与其对称点(i′,j′)按照第1.2 节所述的径向坐标变换方式计算其局部二值模式和编码值,其中,点(i,j)编码值记为F1,点(i′,j′)编码值记为F2.为了确保点对模式编码与旋转无关,有必要按照大小排序关系进行组合.如果F1>F2,则点对模式表示为(F1,F2),否则表示为(F2,F1).统计圆环内所有点对,按照出现频率即可获得该圆环内所有点对模式的直方图描述,记作hm.根据组合关系,模式对有162=256 种组合,因此,hm是一个256 维的特征向量.考虑到对称性,实际计算时,点(i,j)只需要在圆环上半部分取样,这可以避免不必要的重复统计.

影响模式对统计稳定性的因素主要有两个:一是ROI 区域中心位置估算误差,二是图像噪声和干扰.为了获得稳定的统计结果,我们不是直接统计单个点对的直方图,而是在当前点(i,j)和对称点(i′,j′)一定邻域内各自寻找代表性模式作为该点的模式表示.根据实际图像不同的特点,我们设计了两种方式.

· 如果圆形图案纹理细节信息比较丰富,则我们采用主模式选择编码.即:在点(i,j)的M×M邻域内统计出现次数最多的编码模式值,将该模式值作为点(i,j)的代表模式,记为F1;同样统计对称点(i′,j′)的代表模式,记为F2,我们将这种特征提取方式称为邻域代表模式;

· 如果圆形图案主要由线条、边缘轮廓构成,没有丰富的纹理细节,则我们采用主梯度选择编码.即:寻找点(i,j)的M×M邻域内梯度幅值最大的点,并取其径向变换二值模式值作为点(i,j)的代表模式,记为F1;按同样原理确定对称点(i′,j′)的代表模式,记为F2.我们将这种特征提取方式称为邻域主梯度代表模式.需要注意的是,在计算梯度时,同样应该在新的局部径向r,t坐标系统内进行计算,这样才能保证旋转不变性.

将圆形物体所在的ROI 圆形区域按等面积划分为n个交叠圆环,计算每个圆环内的对称结构模式对;然后统计圆环内的特征模式对直方图,记为hm(256 维的特征向量);最终,按从内环到外环的顺序组装起来得到最终的图像特征描述:

其中,hm表示第m个圆环的特征向量,m=1,2,...,n.

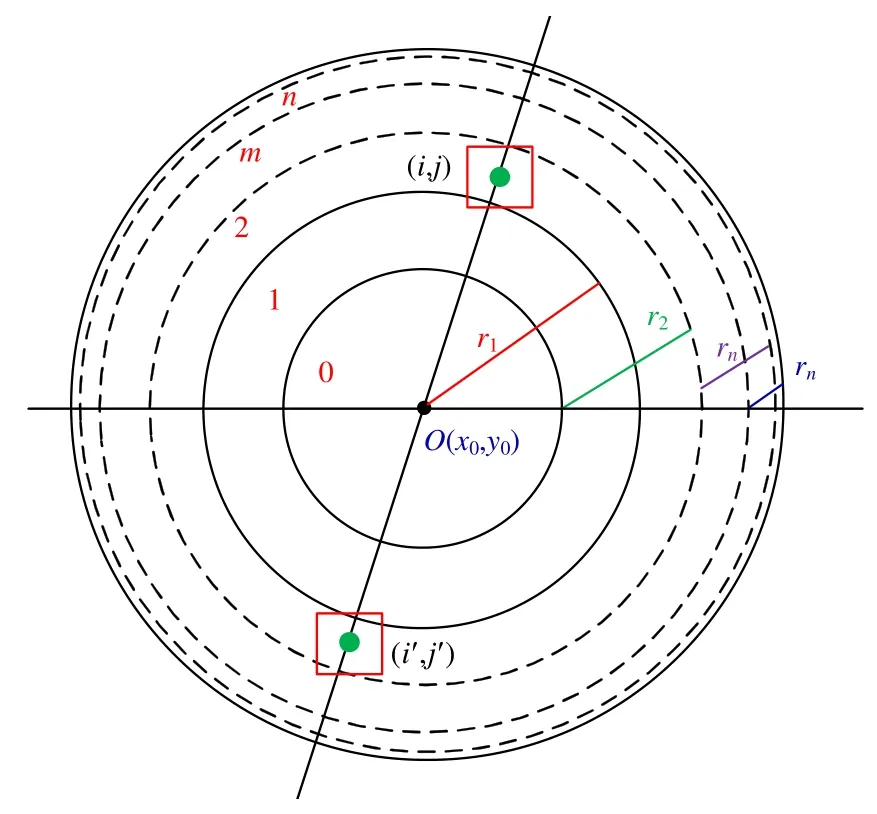
Fig.8 Schematic diagram of symmetrical structure图8 对称结构模示意图

1.4 抗旋转对称结构模式特征提取算法

抗旋转对称结构模式特征提取算法步骤如下.

1)提取圆形图像ROI 区域,并确定其中心位置;

2)对于ROI 区域内每个点,按照局部径向坐标变换选取4 个邻域点,并采用近似计算方式,计算该点的抗旋转编码模式值;

3)将整个ROI 区域按照等面积的原则划分出相互交叠的n个圆环;

4)依次统计第m个(m=1,…,n)圆环内关于圆形区域中心点O对称的点对(i,j)与(i′,j′)的模式,并选择主模式编码或主梯度选择编码方式,统计完圆环内所有点对后,按照出现频率即可获得该圆环内所有模式对组合的直方图描述,记作hm;

5)将n个圆环提取到的特征向量,按照从内环到外环顺序组装得到最终的图像特征描述,记为

2 实验结果及分析

2.1 实验数据集介绍

实验采用了欧元硬币、QQ 表情和车标这3 个数据集.欧元硬币数据集由12 个主要欧盟国家的欧元硬币组成,所有国家硬币正面图案相同,反面图案由每一个国家自行设计,均不相同.硬币数据集包含2 欧元、1 欧元、50 欧分、20 欧分、10 欧分5 种币值,我们采集了不同币值的正反面硬币图像8 430 张.其中,2 欧元2 603 张,1欧元2 240 张,50 欧分1 030 张,20 欧分1 291 张,10 欧分1 266 张.图9 给出了德国、卢森堡和葡萄牙的5 种币值的反面图案.硬币检测的目的是通过识别反面图案实现硬币国别的判别.

QQ 表情数据集是截取腾讯聊天软件中的表情获得的,共包括52 种不同的表情,每种表情图片按5 度加以旋转,可扩充为72 张图片,总共获得3 744 张图片.QQ 表情图片示例如图10 所示.

车标数据集通过对各种车型的网上实物图像截取、建立.我们专门选择了15 种近似圆形的车标图案,其中,每种车型截取了100 张图片,共1 500 张,部分车标图片如图11 所示.

Fig.9 Part of the euro coin figures图9 部分欧元硬币图片

Fig.10 Part of QQ expression pictures图10 部分QQ 表情图片

Fig.11 Part of the car logo pictures图11 部分车标图片

表1 给出了3 个数据集的基本信息.我们之所以采用上述3 个数据集,是因为这3 个数据集有各自不同的特性.它们在色彩、纹理、光照、图案复杂程度方面有明显差异,这可以充分检验方法的适应性和鲁棒性.

Table 1 Experimental dataset basic information表1 实验数据集信息

数据图像中目标的ROI 圆形区域对本文算法特征提取具有重要作用.由于欧元硬币图像有确定的单一背景,通过简单的背景差分和形态学操作,较容易确定硬币的位置和ROI 区域.而对于QQ 表情和车标图片,由于我们重点关注的是圆形图像识别的问题,因此在收集数据集时,我们已经人为地将圆形图像目标从原图中剪切并保存下来,后续算法只需在剪切下来的方形子图中做内切圆即可确定其ROI 圆形区域.

2.2 实验结果与分析

本文方法是基于圆形图像呈现中心对称的特点而设计的,通过径向变换技术和邻域模式选择策略,特征表达对于旋转和噪声具有较强的鲁棒性.因此,该方法命名为“中心-对称鲁棒二值模式”,简记为CS_RBP(central symmetry robust binary pattern).由于本文方法和传统的LBP方法以及HOG 方法在特征提取和采样方式上相似,因此我们主要比较LBP,HOG 方法,以及采用类似的中心对称结构和邻域模式选取策略的LBP 方法和本文提出的CS_RBP 方法在欧元硬币数据集、QQ 表情数据集和车标数据集这3 个圆形图案数据集上的实验结果.其中,分类器模型选择的是线性SVM.

2.2.1 关键参数选取实验

有两个重要参数对CS_RBP 方法检测性能影响较大:一是环形空间的数目;二是在选择邻域代表模式时,邻域窗口的大小.为了获得最佳识别性能,有必要通过实验方式确定合适的参数值.以硬币图像为例,表2 给出了将硬币图像归一化为200×200 后,邻域M×M取为3×3,5×5,7×7,9×9,11×11 这5 种模式,圆环个数m分别取16,18,20,22,24,26,28 等情况下的硬币国别识别结果.

Table 2 M×M neighborhood size and number of rings m selection experiment表2 M×M 邻域大小及圆环个数m 选取实验

从实验结果观测可知,邻域大小的选取比环状空间数目更为重要.在同等邻域大小下,环状空间数目对识别性能的影响比较小,检测结果波动幅度很小.表2 中,每一行加粗的数据是在该邻域大小下,在某环状数目下的最好识别结果.在3×3 邻域时,环数为20,22,24 时有最好结果;而在5×5 邻域时,环数为28 时有最好结果;7×7 邻域时,环数为26 时有最好结果;9×9 邻域时,环数为16 时有最好结果;11×11 邻域时,则环数为28 时有最好结果.在同等邻域下,环数取多少有最好结果没有明显的规律.同时可观测到:随着邻域增大,9×9 和11×11 两组实验结果的波动相对比邻域窗口较小的3×3,5×5 和7×7 的实验结果波动幅度要大一些.另外,观测每一列的数据可知:在环数固定后,邻域过大和过小都会导致识别性能下降.在所有7 列数据中,除了环数22 时,5×5 邻域有最好结果外(下划线数据),其他列中均是在邻域7×7 时取得最佳识别性能.最终的最好识别结果为100%,其中邻域为7×7、环数26.鉴于上述实验结果,7×7 邻域、环数26 是一组较佳的参数.在后续实验中,我们均选用该组参数进行实验测试和比较.

2.2.2 不同算法在3 个数据集上的实验

针对欧元硬币数据集、QQ 表情数据集和车标数据集,我们分别采用不同比例的训练样本进行实验.用来比较的LBP 特征是最常用的LBP 统一旋转不变模式,选取了(p,r)=(8,1)和(p,r)=(8,2)两组参数.在我们的CS_RBP 方法中,模式编码时选取了d=1 和d=2 两组参数.同时,考虑到本文方法改进时所采取的对称结构、邻域代表模式等手段同样可用于原来的LBP 特征提取,因此,也可以结合对称模式实现单点、基于邻域的代表模式或主梯度代表模式这3 种算法形式,因此,我们总共比较了单点、邻域代表模式、邻域主梯度代表模式、单点、邻域代表模式、邻域主梯度代表模式、CS_RBP4,1单点、CS_RBP4,1邻域代表模式、CS_RBP4,1邻域主梯度代表模式、CS_RBP4,2单点、CS_RBP4,2邻域代表模式、CS_RBP4,2邻域主梯度代表模式等算法.此外,本文方法和实验所用的LBP 类方法均属于密集采样,与传统HOG 特征方法的描述方式相似,因此,HOG 特征描述也是一种适合和本文特征方法对比的方法.表3～表5 给出了上述方法在不同训练集占比下对硬币、QQ 表情和车标进行识别的实验结果.为了在7×7 邻域、环数26 参数下取得好的结果,其中图片尺寸均归一化为200×200.在灰度欧元硬币数据集上,提取的特征维数为260 维,单点、邻域代表模式、邻域主梯度代表模式的特征维数1 320 维,CS_RBP单点、CS_RBP 邻域代表模式、CS_RBP 梯度邻域主梯度代表模式的特征维数均为3 536 维,在彩色QQ 表情数据集和车标数据集上,分别提取R,G,B 这3 个通道特征,再合并为一个最终特征,此时提取的特征维数为780 维、单点、邻域代表模式、邻域主梯度代表模式的特征维数3 960 维,CS_RBP单点、CS_RBP 邻域代表模式、CS_RBP 梯度邻域主梯度代表模式的特征维数均为10 608 维.HOG 特征的block单元由8×8 像素构成,2×2 个block 构成一个cell 单元,最后提取的特征维数为20 736 维.表3～表5 中给出了不同方法在3 个数据集上的测试结果,其中,占比是指即训练样本集占总数据集图片的比例.

由表3～表5 可以看出:在3 个数据集上,所有方法被分成5 组,其中,第1 组为表中第2 行,第2 组为表中第3行、第4 行,第3 组为表中第5 行～第8 行,第4 组为表中第9 行～第12 行、第5 组为表中第13 行～第16 行.在传统LBP 方法组中,方法的识别率高于方法,说明适当增大邻域半径可以捕获更多的邻域信息,对于提高识别率有帮助.在不采用邻域选择策略的单点模式对方法组中,在3 个数据集上,单点与CS_RBP 单点的方法普遍表现较差.原因在于:一是图像ROI 区域中心位置估算存在误差,二是图像本身噪声的干扰.此时,直接将该点的编码值作为模式值难以获得稳定的特征表达.但是CS_RBP 单点方法性能仍高于单点方法,原因在于CS_RBP 可以编码16 种模式,多于方法的10 种模式,能表达图像更多的细节信息.此外,在3 个数据集上,CS_RBP 的邻域代表模式方法与邻域主梯度代表模式方法的识别率也均高于的邻域代表模式方法与邻域主梯度代表模式方法,充分说明CS_RBP 方法特征的鉴别能力强于传统LBP 特征模式.表明采用局部径向坐标变换技术后,同样是基于邻域选择策略的主模式,具有16 个模式种类的CS_RBP 优于只有10 个模式种类.同时,在,CS_RBP 方法中,基于邻域的代表模式均远高于其对应的单点类的方法,表明基于邻域选择策略的代表模式鲁棒性强,能够很好地克服图像ROI 区域中心位置估算误差以及图像本身的噪声与干扰的影响.

Table 3 Euro coin recognition accuracy表3 欧元硬币数据集识别率

Table 4 QQ expression recognition accuracy表4 QQ 表情数据集识别率

Table 5 Car logo recognition accuracy表5 车标数据集识别率

LBP 方法比较适合提取纹理特征,但是在纹理信息比较缺乏的QQ 表情和车标数据集中,对应的LBP 方法的性能远低于本文的方法.这也说明本文方法适应性强,对于纹理丰富和纹理缺乏的图像均能适用.值得注意的是:邻域半径增大后,很多时候CS_RBP4,2并没有取得CS_RBP4,1更好的性能,反而还有所下降.原因是局部径向坐标变换的旋转不变二值模式的近似计算在半径增大后,计算误差会增加,尤其是当图像邻域中含有细节纹理信息时,例如在含有较多纹理信息的硬币数据集和因为色差产生的具有纹理变化的QQ 表情数据集测试时.

由表3～表5 可知:在训练集占比为8%的欧元硬币数据集与占比为16%的QQ 表情数据集上,能够达到的最好识别率100%均为本文方法所取得;只有在车标数据集中,获得的最好识别率100%由HOG 方法取得.同时,我们可观察到:只需要较少比例的训练样本,例如欧元硬币数据集中训练集占比为8%、QQ 表情数据集中训练集占比16%,本文方法均达到100%的识别率.但是对于车标数据集,尽管车标图案不旋转,但是由于图像在自然场景下获取,背景、照明和视角均有较大变化,因此仍然需要较多的训练样本,本文方法才能保证其识别性能.

由于HOG 特征本身没有考虑旋转不变性问题,因此其对于旋转图案识别效果不理想,特别是在样本数较少的情况下,由于样本很难涵盖各种旋转角度,此时HOG 方法识别性能较差.例如在硬币数据集中,在训练样本数为2%时,HOG 特征识别率只有57.46%,而LBP 和CS_RBP 邻域代表模式能达到90%以上的识别率;在训练样本数为4%时,HOG 特征识别率只有67.73%,而LBP 和CS_RBP 邻域代表模式多数情况能达到95%以上的识别率;在训练样本数为8%时,HOG 特征识别率虽然可以达到83.44%,但是仍远低于LBP,CS_RBP 邻域代表模式和邻域主梯度代表模式的识别率.在QQ 表情图像集中,相似的情况也能在HOG 方法和CS_RBP 邻域主梯度代表模式中观察到.但是对于车标数据集,由于车标图像本身无旋转变化且边缘结构信息显著,此时HOG 特征表现优异,在训练样本占比15%,30%,45%这3 种情况下都得到了100%的识别准确率.这是因为HOG 特征描述利用的是梯度信息,其在对抗照明变化上要优于LBP 和CS_RBP 特征方法.但是一旦图像发生旋转,则HOG 特征的性能难以得到保证,这在欧元硬币的检测和QQ 表情数据集中已经得到验证.

2.2.3 计算效率比较

CS_RBP 作为二值描述算子,计算原理简单,与其他二值描述算子一样具有高效的优点.表6 给出了几种代表性的浮点数值型描述子HOG,SIFT 和SURF,以及二值描述算子BRIEF,FREAK 和本文CS_RBP 方法在进行单点特征提取所花时间的比较.其中:HOG 单个Cell 特征提取约耗时1.9ms;SIFT 和SURF 算子需要2.5ms 和1.4ms;而CS_RBP 方法只需0.045ms,效率是HOG 的42 倍、SIFT 的56 倍、SURF 的31 倍.由于CS_RBP 在寻找对称模式时计算原理比BRISK 和FREAK 复杂一些,因此时间消耗上略有增加.CS_RBP 算法运行环境:CPU为i5-4590,4GB 内存,Matlab 2014a.

Table 6 Comparison single point feature extraction time of different descriptors表6 描述子单个点特征提取时间比较

2.2.4 抗旋转性能测试

为验证本文算法特征的抗旋转特性,以德国2 欧元硬币背面图像为例,如图12 所示,分别提取初始样本和旋转不同角度后该硬币图像的特征,特征向量之间的相关度由公式(6)计算:

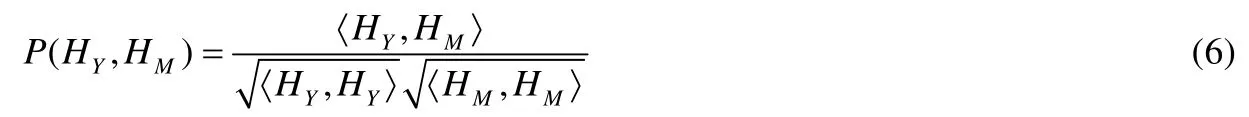
其中,HY和HM分别表示初始样本图片和旋转后图片的特征向量,〈·,·〉表示向量内积.

Fig.12 Test picture rotation schematic图12 测试图片旋转示意图

P(HY,HM)表示HY和HM的相关系数,可以衡量特征的抗旋转能力,平均相关度越大且标准差越小,则抗旋转性越强.每次旋转15 度,我们计算了原始图像和旋转后图像的特征相关度,表7 给出了本文4 种方法和LBP,HOG特征在图像旋转后的相关度值.

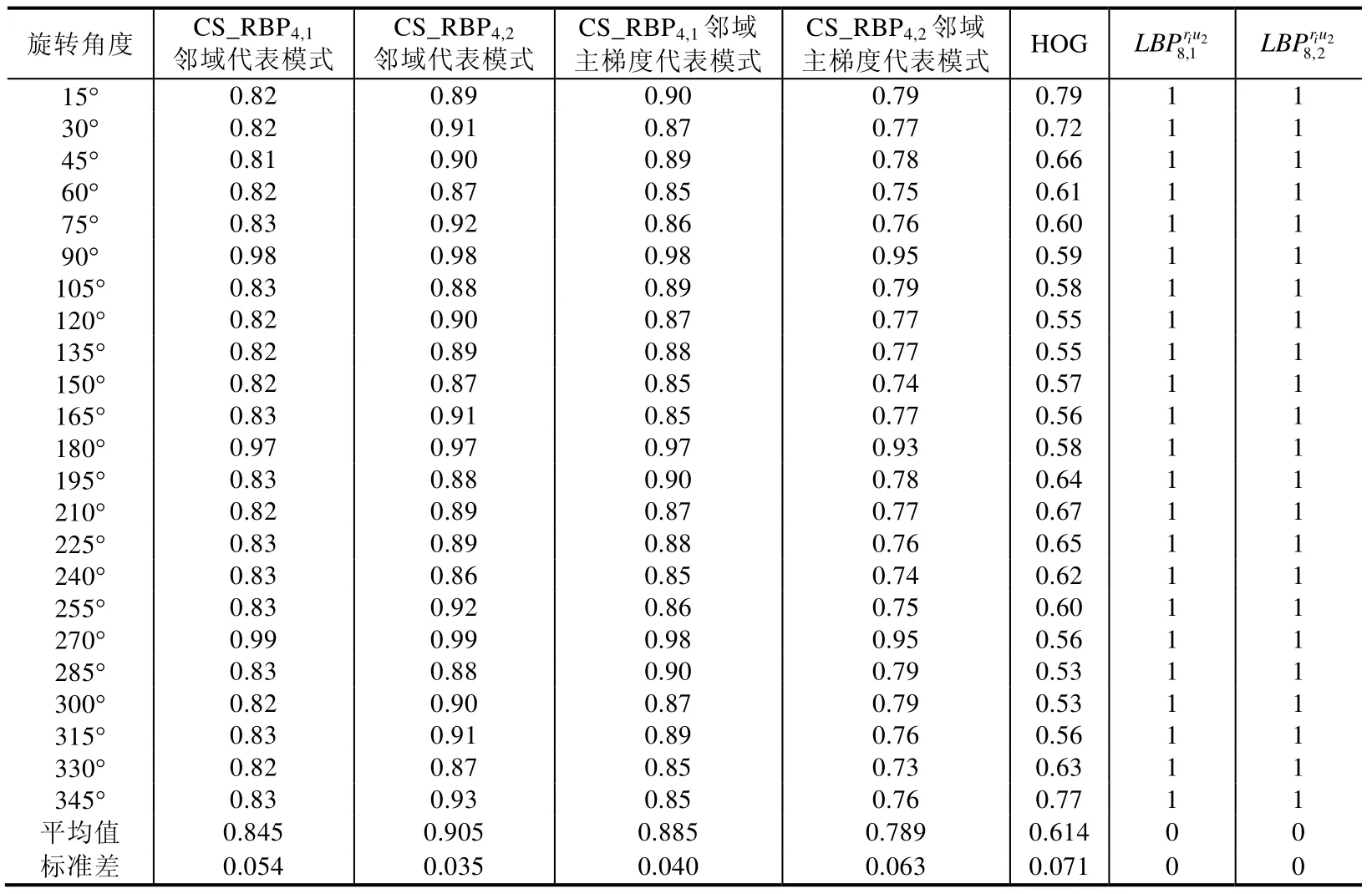
Table 7 Average correlation of the features after rotation of the sample images表7 样本图片旋转后的特征平均相关度

从表7 可知,本文的4 种算法在每个旋转角度的相关度均比HOG 特征高,同时标准差也较小.本文4 种算法的平均相关度分别为0.845,0.905,0.885,0.789,远高于HOG 特征的0.614,其中,CS_RBP4,2邻域代表模式表现最为稳定,平均相关度值达到0.905,标准差0.035.LBP 特征模式我们采用的是旋转不变模式,因此其本身具有旋转不变性,在所有旋转角度情况下,其特征相关度均为1.尽管如此,但是LBP 旋转不变模式信息损失较大,不利于图像细节的描述,因此特征的鉴别能力不足.而本文方法在尽可能保留抗旋转描述特性的同时,利用空间对称位置结构信息有效提高了特征的鉴别能力,从而达到抗旋转高鉴别二值模式特征提取的目的.

2.2.5 原始特征计算方法和近似计算方法对比

在基于局部径向坐标变换的旋转不变二值模式计算时,我们采用了近似计算方法.为了验证近似方法的可靠性,与原始算法进行了对比测试.考虑到原始特征计算方法相当耗时,我们只选取了部分欧元硬币进行实验,其中,2 欧元硬币580 张,1 欧元硬币552 张,50 欧分硬币252 张,20 欧分硬币312 张,10 欧分硬币312 张,实验结果见表8.

Table 8 Initial feature calculation method is compared with the recognition result of approximate calculation method in euro coin recognition表8 原始特征计算方法与近似计算方法在欧元硬币识别上的识别结果对比

从表8 可看出,4 种情况下的原始特征计算方法与近似计算方法上在最终的分类精度上相差无几;而近似计算方法由于避免了大量的浮点数插值计算,从而大大提高了计算效率;原始特征计算方法对200×200 大小的图像进行的特征提取耗时约30s,而近似计算办法耗时仅需1s.

3 总结

针对圆形图案中心对称的特点,本文提出一种基于空间对称结构模式对的图像二值特征描述方法.由于引入了局部径向变换技术,在抗旋转特性的同时,使得能够表达的基本模式达到16 种,多于的10 种模式,因此能够更多地描述图像的微观结构细节信息;并且通过组成对称模式对,充分利用了圆形图像的空间结构信息,因此提升了特征的鉴别能力.在具有旋转情况的欧元硬币和QQ 表情数据集上,均取得了优于原LBP 特征和HOG 特征提取方法的识别性能.由于算法专门针对旋转的圆形物体图像识别问题,因此CS_RBP 方法在抗旋转能力上具有很强的鲁棒性.在训练集占比为8%的欧元硬币数据集与训练集占比16%QQ 的表情数据集中,本文方法均达到100%的识别率.说明本文方法只需少量的代表性训练样本即可达到良好的性能,不需要存储大量的不同旋转角度的训练样本集.此外,CS_RBP 作为一种高效的二值描述算子,具有和其他二值描述算子一样的优点.单点计算时间只需0.045ms,效率是HOG 的42 倍、SIFT 算子的56 倍、SURF 算子的31 倍.