明安图对交错级数的表述及处理
王鑫义,郭世荣
(内蒙古师范大学 科学技术史研究院,内蒙古 呼和浩特 010022)
明安图(1692—1763?),字静庵,蒙古族,奉天正白旗(今内蒙古正镶白旗)人,清代著名的数学家、天文学家、测绘学家。他研究由杜德美(P.Jartoux,1668—1720)传入的3个无穷级数长达30年,1730年前后开始著《割圆密率捷法》(以下称《捷法》),临终时留下《捷法》(四卷)初稿,经由罗士琳、岑建功等校勘后于1839年正式出版。《捷法》是中算史上第一部将三角弦矢函数展开为无穷级数的著作,卷一主要讲了“杜明九术”,卷二中首次将无穷级数应用于天文计算。以往的数学史研究者对明安图的生平事迹及其数学贡献做了详细考究[1-4],并运用“翻译”和算理分析等方法对《捷法》卷三和卷四中的算法理论做了相当多的研究[5-14]。《捷法》卷一的“杜明九术”中有五术为正项级数,其余四术为交错级数,在“弧背求正弦”、“弧背求正矢”、“弧背求通弦”、“弧背求矢”四术中,“弧背求正弦”与“弧背求通弦”的算法相同,后者只是比前者的各项都多出除以四,“弧背求正矢”与“弧背求矢”的算法相同,后者只是比前者各项都多出除以四,因而本文只对“弧背求正弦”与“弧背求正矢”两术做具体分析。
1 梅瑴成在“求正弦正矢捷法”中的左右书写形式及处理方法
梅瑴成(1681—1763)把法国传教士杜德美于1701年带来的3个无穷级数展开式收入《赤水遗珍》中,只称“译西士杜德美法”,并在“求正弦正矢捷法”中列举了求正弦二例和求正矢一例。“求正弦正矢捷法”实为两个关键展开式,以“设弧二十一度十九分五十一秒,半径八位,求其正弦”为例:
“以第一得数与第三得数相并。又以第二得数与第四得数相并。末以后并数减先并数,余三六三七五二五四。截去末一位,即所求之正弦也。”[15]
梅瑴成将每次计算的得数分类处理,先把奇数类加和,偶数类加和,再进行做差运算。原文中蕴含着具体的运算步骤,并配有相应的图式,做到图文对照,如下图:
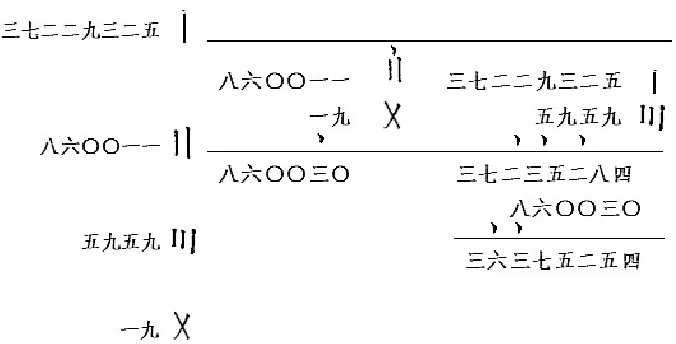
图1 “求正弦”一例中的分类处理方法Fig.1 Pictures in Chi Shui Yi Zhen
在上图的左半部分中,梅瑴成用“丨”表示第一得数(37229325),记于第一得数的右边,用“”表示第二得数(860011),记于第二得数的右边,后仿此。用各数码表示与之对应的各得数的序号,这样不同的表示方法,是为了便于区分各得数。在上图的右半部分中,梅瑴成先将第一得数与第三得数(5959)加和,第二得数与第四得数(19)加和,奇数类得数记于右边,偶数类得数记于左边,再将所得的和做差运算。在具体运算的过程中,各得数旁边的数码继续用上图左边的表示方法对应标记,以防混淆奇偶类得数。
2 《捷法》中的具体记述及处理方法
2.1 关于“弧背求正弦”的记述
明安图在《捷法》卷一的“弧背求正弦”中对具体的运算操作进行了充分阐述,从文中可以看到他的处理方式:
“以弧背本数为第一条。次以半径为连比例第一率,弧背为连比例第二率求得连比例第三率。次置第一条,以三率乘之、一率除之,得第四率数。二除之,又三除之,得数为第二条,应减,另书之。次置第二条,以三率乘之,一率除之,得第六率数。四除之,又五除之,得数为第三条,应加,书于第一条之下。次置第三条以三率乘之、一率除之,得第八率数。六除之,又七除之,得数为第四条,应减,书于第二条之下。……,第一条、第三条、……相并,第二条、第四条、……相并,两总数相减,得数即正弦。”[16]
据罗见今在《捷法》译注中的记法[4],将“弧背求正弦”公式(格列高里1667年所创)表示为:
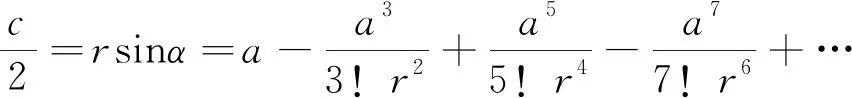
(1)
第n条un为展开式第n项(n=1,2,…),令u1=a,有:
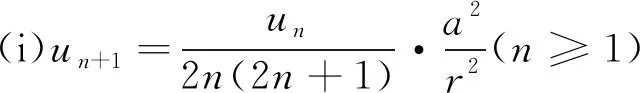
(2)
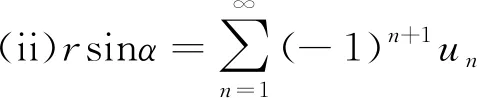
(3)
可将式(1)记为
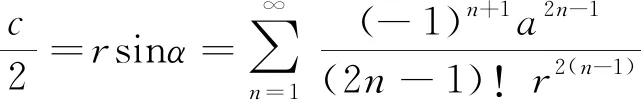
(4)
将各项按原文要求分类处理,见表1。
明安图将“弧背求正弦”中的奇数项记为正,偶数项记为负,一加一减,正负相间,将此交错级数记为Mn1:
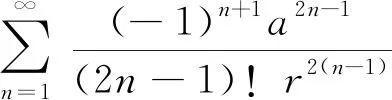
(5)
为计算各项正负相间的值,他将正值(条数为奇)记在右边(或上面)相加,将负值(条数为偶)在左边(或下面)相加,两和再相减。
若记Mn1=u′-v′,(n≥1)
(6)
则有
u′=u1+u3+u5+…+u2n-1+…
(7)
v′=u2+u4+u6+…+u2n+…
(8)
其中,u′为右边奇数条相并后的总数,v′为左边偶数条相并后的总数,Mn1为两总数的差。

表1 正负项的左右书写形式Tab.1 Right and left writing form in Jie Fa
2.2 关于“弧背求正矢”的记述
据《捷法》卷一“弧背求正矢”中的记载:
“以半径为连比例第一率,弧背为连比例第二率,求得连比例第三率。二除之,得数为第一条。次置第一条,以三率乘之、一率除之,得第五率数。三除之,又四除之,得数为第二条,应减,另书之。次置第二条,以三率乘之、一率除之,得第七率数。五除之,又六除之,得数为第三条,应加,书于第一条之下。次置第三条,以三率乘之、一率除之,得第九率数。七除之,又八除之,得数为第四条,应减,书于第二条之下。……,第一条、第三条、……相并,第二条、第四条、……相并,两总数相减,得数即正矢。”[16]
按罗见今在《捷法》译注中的记法[4],则有:
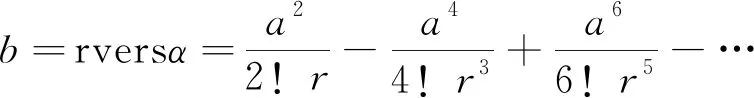
(9)
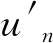
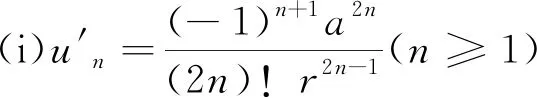
(10)
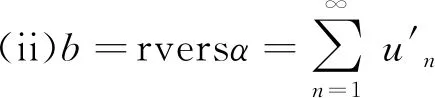
(11)
可将式(9)记为
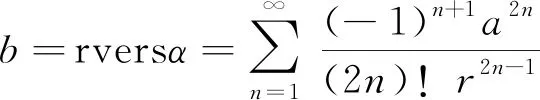
(12)
将各项按原文要求分类处理,见表2。

表2 正负项的左右书写形式Tab.2 Right and left writing form in Jie Fa
将此交错级数记为Mn2,则
Mn2=b=rversα=
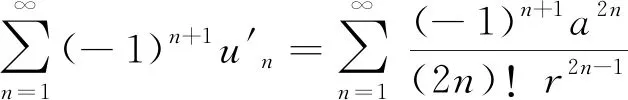
(13)
若记
Mn2=u″-v″,(n≥1)
(14)
则有
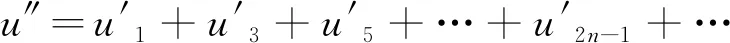
(15)
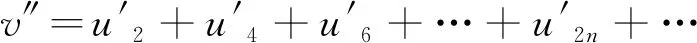
(16)
其中,u″为右边奇数条相并后的总数,v″为左边偶数条相并后的总数,Mn2为两总数的差。
2.3 卷二中的左右书写形式及处理方法
据《捷法》卷二“角度求八线”中的记载:
“弧背为第一条,书右。……第二条,书左。……第三条,书右。……第四条,书左。每次得数降二位,第四条数尚有三位,须求第五条数。……第五条,书右。第五条数止一位,第六条数必在小余下,故可省求。次并右三条,…,并左二条。置右总数减左总数,……。在旧法当一减一加累求之。今以应加者书右,应减者书左,只用加二次、减一次,较为省便。”[16]
与卷一中不同的是,文中将“角度求八线”中的各条数用相应的算式来表述:
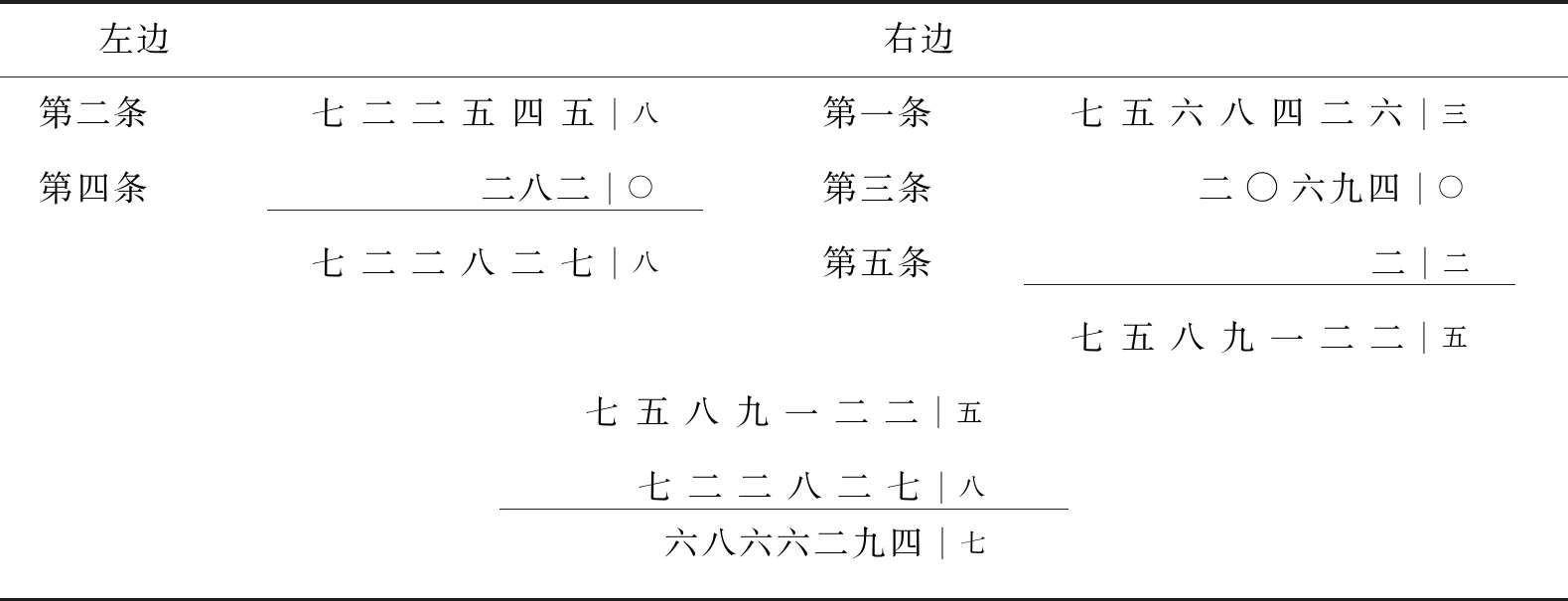
表3 奇偶数条的左右书写形式Tab.3 Right and left writing form of odd and even entries in Jie Fa
明安图将交错级数看作是两个正项级数做差的运算,认为在处理交错级数的过程中,一加一减容易混淆正负项,计算的过程相对比较繁杂,而经这样处理后,不仅能大大减少运算量,较为省便,且不容易混淆出错。
2.4 岑建功对此类处理方法的相关记述
岑建功在校勘《捷法》时提到,《赤水遗珍》中所辑录的公式精密便捷,并在《捷法》卷一的“弧背求正弦”中明确讲到了这种处理方法的源起:
“建功案:此加、减乃西法通例也。若援古开方例,以正负别加减,于二、四、六、八等应减之条为负数,用斜画作志,似较另书之例甚便,且无混淆之虑。”[16]
明安图将应加与应减的条数分开布列,岑建功补充说:这种将正负条数分开标记的方法实属西法,在古代的开方法中,区分正负的方法是把二、四、六、八等应减去的各条用一斜画为记号作为负数,比“另书之”较为方便,更不容易混淆。李冶发明的负号,通常画在最后一位有效数字上,也就是在最后非零的数码上画一“”号[17],李冶用一斜划在数字上表示负数的这种记法和他以前的赤、黑筹记法相比是一种改进。显然,岑建功在对比了中西正负数表示法后,认为用一斜画做记号的方法更简、更优,一方面没有跟从或效仿明安图的做法,没有认识到这样分类处理的便捷之处,另一方面他认为焕然一新的表示法是对传统表示法的一种破坏。“另书之”的方法与现今的加法竖式运算极为相近,较之以前的正负数记法来说,不仅摆脱了以往算筹对位置极大的依赖性,而且使得各位数字对齐也为计算提供了便利。
梅瑴成在《赤水遗珍》中辑录的3个无穷级数展开式没有证明和推导过程,明安图得知此事后,以“仅有其法而未详其义,恐人有金针不度之疑”[16]之由,开始研究“杜氏三术”。1713年前后,明安图开始在钦天监工作,1721年前后梅瑴成与明安图、何国宗等人同在蒙养斋学习,明安图知晓梅瑴成所辑录的“杜氏三术”是受了西法的影响,在处理此类问题时借鉴了梅瑴成所用的处理方法,并在他的基础上加以发挥,将交错级数看作是两个正项级数做差的运算。无穷级数涉及的项数较多,运算量较大,斜画“”等记法对单项式和多项式正负项的区分较为便利,对无穷级数来说,不一定能起到优化的作用,而这样正负左右分开的记法还带有明显的分类、归类的目的,不仅减少了运算次数,而且不容易混淆各项的正负。可以说,这在认识上是进步的,技术上也是先进的。
3 明安图对收敛性问题的认识
若《捷法》卷一中的四术满足:
(i)各项是单调递减的,即un+1 则此交错级数为莱布尼兹级数。 此类交错级数的敛散性,可以通过以上两个条件进行判别,这种判别法称为莱布尼兹判别法,或称为莱布尼兹定理[18],或称为莱布尼兹准则[19]。可知Mn1和Mn2均满足莱布尼兹级数的两个条件,故而Mn1和Mn2为莱布尼兹级数,同理可得“弧背求正弦”、“弧背求正矢”、“弧背求通弦”、“弧背求矢”四术中的交错级数均为莱布尼兹级数。 而明安图在《捷法》卷二“角度求八线”中先求得弧长,再将弧长的值代入“弧背求正弦”的级数展开式中去计算,通过表3中各条数的变化可以看到各项数值在依次减小。在卷二的其他题目中,所用的方法都与“角度求八线”的方法相同,且其他题目中的各项也都是依次减小的。在卷二的实际问题中,如“第五条数止一位,第六条数必在小余下,故可省求”[16],“第二条得数仅二位,而比第一条数降四位,则第三条数必降至奇零下,即无庸求”[16]。即是说,通过降位当计算到出现纯小数时,便停止计算。就他对交错级数的运用来看,有以下几个特点: 1)只计算有限个条数的和与差,终极目标则是为解决实际问题。 2)对计算结果的变化规律已有了很清楚地判断,并能预见计算结果。 3)无限多个条数的和与差对他来说是一个新概念,未能澄清自己对何谓无限多个条数的和与差的认识。 4)借助分类的方法将无限多个条数的和与差转化为有限个条数的和与差,虽无限多个条数的和与差与所处理的有限个条数的和与差相联系,但在这里二者是孤立的。 5)所处理的交错级数都相当于单调减少有界的,且都恰好是(绝对)收敛的。 6)虽各项的绝对值趋近于0的条件比分析学中讨论级数敛散性的条件弱,但对级数收敛有了一定的认识。 明安图用这种新颖的分类方法来处理交错级数,所带来的效果是显而易见的。简洁便利的实现得益于分类化的处理,将不再依赖于原有做记号的正负项标记形式,而分类化的处理方式又被往后的中算家所极力效仿,这也是明安图积极学习西算中的处理方法的有益尝试。 因为级数是有限和的推广,有鲜明的直观性[20]。卷二中明安图通过有限项的计算进而把握无限项的变化,将直观基础用于交错级数的计算,很好地判断计算结果的变化规律,反映了他对级数收敛的认识。不过对级数收敛性的认识较为模糊,缺乏分析的说明,也未能给出级数收敛的相关条件。他把函数级数看作是数值级数来对待,几乎与多项式类似,实际上是把多项式运算形式地平移到级数中来的结果[21],即它仍然只是形式运算[22]。这样分类处理意在简化运算,因而没有热衷于深究与此无关的性质。把幂级数看作无穷多个项的多项式是很方便的,可以先不考虑其收敛性,而把它们当成多项式加以计算,给定两个形式幂级数就可以构成它们的线性组合[23]。 明安图对交错级数的表述及处理源于西法,又缘于梅瑴成在《赤水遗珍》中所使用的分类处理方法,将问题化难为易,化繁为简,这种新形式使我们处理交错级数时具有更大的灵活性,并提供了新方法。他认为一加一减容易混淆正负项,计算的过程相对比较麻烦,而将莱布尼兹级数看成“正部分”与“负部分”之差再进行运算,这样处理相当于构造了两个新的正项级数。然而,他对无穷级数的认识局限于代数中多项式的有限次加减运算,在实际应用问题中只给出满足精度的有限项数,未能说明这样分类处理及运算的合理性,也没有详细说明这样处理的前提是分解成的无穷级数都收敛。这毕竟还是在形式级数本身的“弹性限度”内,也正因如此,将运算结果推广至无穷项后,运算仍是可行的,结果仍是准确的。 致谢特别感谢审稿专家所给的修改意见。此外,本文得到罗见今教授的帮助,也得到2017年第七届数学史与数学教育研讨会参会师友的建议,在此一并致谢。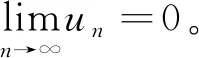
4 结 语

