借助于“运动” 架设好“桥梁”——例说全等三角形的构造

文丁建生

证明三角形全等或通过证明三角形全等进而证明线段、角等之间的关系是这一章中典型的问题。当全等三角形的条件很具体、直接、明显时，这类问题很好解决，只需要我们识别图形并规范、认真作答，做到步步有据即可。然而，有时题目中的全等三角形不是一眼就能看出来的，需要我们挖掘、构造。构造的过程其实就是在原有图形的基础上适当连接、添加辅助线的过程，辅助线的作用恰似“桥梁”。而构造全等三角形必须要有方向。从图形的运动（平移、旋转、翻折）出发，是一种有效、可行的方法，下面举例说明。

一、运用平移构造全等

例1如图1，在梯形ABCD中，AD∥BC，对角线AC、BD相交于点O。若梯形的面积为1，试求以AC、BD、AD+BC的长度为三边长的三角形的面积。

图1

【解析】要解决这个问题，应构造一个三角形，使三边的长度与AC、BD、AD+BC相同。平移AC至DE，即过点D作DE∥AC交BC的延长线于点E。由于AD∥BE，不难证得△ADC≌△ECD（ASA），所以AD=EC，AC=ED。故BE=BC+CE=BC+AD。

又因为△ABD与△ACD等积，所以△CDE与△ABD等积。所以△BDE的面积=梯形ABCD的面积=1。

例2 如图2，正方形ABCD中，EF与MN相交于点O，EF=MN，求∠EON。

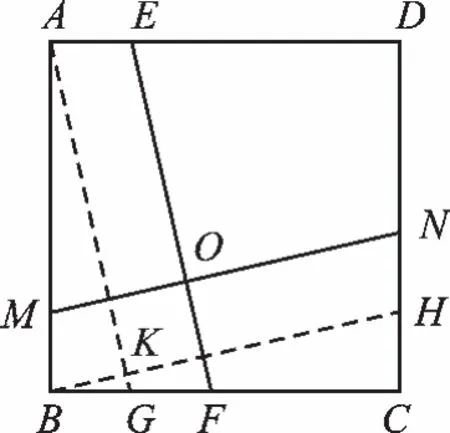
图2

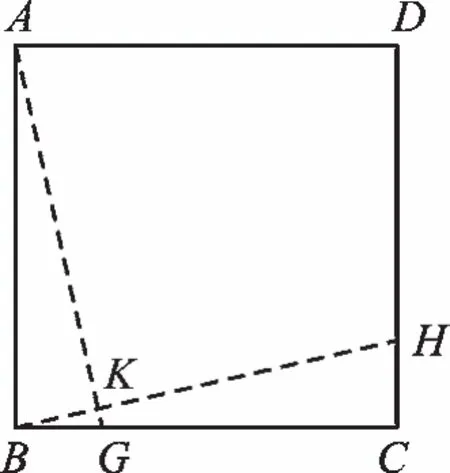
图3

【解析】本题如果是填空或选择题，可考虑特殊状态：EF∥AB，MN∥BC（甚至更特殊的是EF、MN分别与AB、BC重合），则∠EON=90°。

在一般状态下，可联想到基本图（如图3）。正方形ABCD中，若AG=BH，则AG⊥BH；若AG⊥BH，则AG=BH。故在图2中，过B作BH∥MN交CD于H，过A作AG∥EF交BC于G，AG交BH于K，此时不难证明EF=AG，MN=BH，∠AKH=∠EON，这就转变成了图3的问题。故得∠EON=90°。

【反思】平移就是将线段（或图形）平行移动，自然就得到同位角、内错角相等，平移前后的线段相等。通过平移，将角、线段实行了转移，使分散的条件相对集中，构成了全等三角形，促使问题得到迅速解决。

二、运用旋转构造全等

例3如图4，△ABC中，AB=AC，M、N为BC上两点，∠BAM+∠CAN=∠MAN，BM=2，CN=3，求MN的取值范围。

图4

【解析】根据两角和的条件，设法将两角拼在一起。因为AB=AC，故将△ANC绕点A旋转至△APB处，则△ANC≌△APB。∠CAN=∠BAP，AN=AP，CN=BP，易证得△AMN≌△AMP，所以MN=MP。又因为△BMP中，BP=3，BM=2，所以 1＜MP＜5。故1＜MN＜5。

例4 如图5，已知AC∥BD，AE平分∠CAB且E为CD中点，求证：AB=AC+BD。

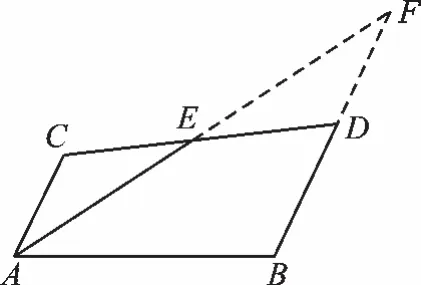
图5

【解析】本题的结论是要求两线段的和AC+BD，故首先要作出或找到AC+BD的线段。因为AC∥BD，所以∠C+∠D=180°，所以将△ACE绕E旋转180°至△FDE处。此时△ACE≌△FDE，所以∠C=∠EDF，∠CAE=∠DFE，AC=FD。所以 ∠CDB+∠EDF=∠CDB+∠C=180°，BF=DF+BD=AC+BD。又因为AE平分∠CAB，所以∠CAF=∠BAF。故在△ABF中，∠F=∠BAF，所以AB=BF，所以AB=AC+BD。

【反思】旋转前后的两个图形是全等的。例3中，通过旋转将分散但有关系的两个角“合并”在一起，这样才能运用题目条件求解相关问题。例4中的旋转有两个前提：CE=DE，∠C+∠D=180°，这才保证了△ACE≌△FDE，∠BDF=180°，这样的旋转才有价值。在图5中，若连接BE，则能得到其他一些结论。同学们，你有什么发现？

三、运用翻折构造全等

例5 如图6，在四边形ABCD中，对角线AC平分∠BAD，AB＞AD，试比较AB-AD与CB-CD的大小。

【解析】因为AC平分∠BAD，所以∠BAC=∠DAC。又因为AB＞AD，故将△CAD沿AC翻折至△CAE处，点E落在AB上。显然△CAD≌△CAE，所以AD=AE，CD=CE，AB-AD=AB-AE=BE。在△BCE中，根据三边关系得BE＞BC-CE，所以AB-AD＞CB-CD。

图6

图7

例6如图7，已知△ABC中，∠A=60°，BE、CD分别平分∠ABC、∠ACB，P为BE、CD的交点，求证：BD+CE=BC。

【解析】所求结论是较长线段等于两条较短线段的和，常规方法是“截长”或“补短”。

因为CD平分∠ACB，故将△CPE沿CP翻折，使E落在BC上为点F（这就是截长），剩下只要证明BF=BD。

【反思】翻折前后的图形一定是全等的。上面两题中的翻折可换一种说法：例5是在线段AB上截取AE=AD；例6是在线段BC上截取CF=CE。在例5中，通过翻折将相关线段AD、CD实行了转移，使问题转化为△BCE的三边关系的问题。在例6中，通过翻折将线段和的问题转化为证明线段相等的问题。

平移、旋转、翻折是图形的三种“运动”，它是解决几何问题的有力工具和重要方法。两个全等三角形组成的图形都可以看成是由一个三角形经过适当的“运动”而得到的。