指数函数图像及性质第一课时教学设计
崔芳
一、教材内容分析
本节课是《普通高中课程标准实验教科书·数学(1)》(人教A版)第二章第一节第二课(2.1.2)《指数函数及其性质》。根据我所任教的学生的实际情况,我将《指数函数及其性质》划分为两节课(探究图象及其性质,指数函数及其性质的应用),这是第一节课“探究图象及其性质”。指数函数是重要的基本初等函数之一,又是第一个呈现在学生面前的函数,它不仅从研究思路、探究方法、及常见应用方面为后面学习对数函数和幂函数打下基础,同时在生活及生产实际中有着广泛的应用,所以指数函数应重点研究。可以说这一课的学习对后面的学习有很大的影响或者帮助。
二、学习者特征分析
指数函数是在学生系统学习了函数概念,基本掌握了函数的性质的基础上进行研究的,是学生对函数概念及性质的第一次应用。教材在之前的学习中给出了两个实际例子(GDP的增长问题和炭14的衰减问题),已经让学生感受到指数函数的实际背景,但这两个例子背景对于学生来说有些陌生。对学生从形象向抽象、由特殊向一般过渡,由学习常量数学到学习变量数学,思维能力的提高是一个转折期,有主动学习的愿望,但很是力不从心.本节课先从一段优美的芭蕾舞视频开始,通过观察归纳舞者的人数发现规律,在轻松的环境下,通过问题来激发学生学习新知的兴趣和欲望。
三、教学目标
本节课我确定的教学目标是:掌握指数函数解析式的特点,能画出具体指数函数的图象;通过具体的指数函数图像、性质尝试对一般规律的概括;最后在理解指数函数概念、性质的基础上,能简单应用其比较两个幂的大小、及解简单的指数不等式。在教学过程中通过类比,回顾归纳从图象和解析式这两种不同角度研究函数性质的数学方法,加深对指数函数的认识,让学生在数学活动中感受数学思想方法之美、体会数学思想方法之重要;同时通过本节课的学习,使学生获得研究函数的规律和方法;培养学生主动学习、合作交流的意识。
四、教学重难点分析
教学重点:指数函数的概念、图象和性质。
教学难点:对底数的分类,如何由图象、解析式归纳指数函数的性质。
五、 教学策略的選择与设计
函数及其图象在高中数学中占有很重要的位置。如何突破这个即重要又抽象的内容,其实质就是将抽象的符号语言与直观的图象语言有机的结合起来,通过具有一定思考价值的问题,激发学生的求知欲望――持久的好奇心。本节课,力图让学生从不同的角度去研究函数,对函数进行一个全方位的研究,并通过对比总结得到研究的方法,让学生去体会这种的研究方法,以便能将其迁移到其他函数的研究中去。
结合我校本学科的教学模式:在“导学--助学”的模式下提倡以问题为中心的教学方法,使学生在课堂活动中通过同伴合作、自主探究培养学生积极主动、勇于探索的学习方式。在教学过程中努力做到生生对话、师生对话,并且在对话之后重视体会、总结、反思,力图在培养和发展学生数学素养的同时让学生掌握一些学习、研究数学的方法。
六、教学环境及资源准备
教师准备: G20峰会晚会天鹅湖片段,几何画板,投影仪,
学生准备:刻度尺、铅笔
七、教学过程
(一)创设情景---提出问题
1、播放G20峰会晚会“天鹅湖”剪辑片段。
2、引导学生观察,每变换一次队形,舞者总人数的变换
思考归纳,若用 表示变换队形的次数,用 表示变换后的人数,找出两个量之间的关系并引导学生思考上述两个函数解析式在形式上有什么共同特点?
设计意图:营造一个轻松的学习环境,从而激发他们的学习兴趣,体会数学源于生活有高于生活还可以引出本节课的课题
(二)自主学习---概念探究
1、给出指数函数的定义(板书))
2、引导学生自己说出几个指数函数?根据定义判定下列函数是否为指数函数?
(1) (2) (3) (4)
3、若 是指数函数,则 取值为 。
4、指数函数定义中,为什么规定“ ”否则会出现什么情况?
设计意图:使学生巩固概念,深化认识,强化对概念形式特征的把握,感知数学概念的严谨性和科学性同时准确把握与旧知识的连接点.
(三)绘制图像---探究指数函数图像及性质
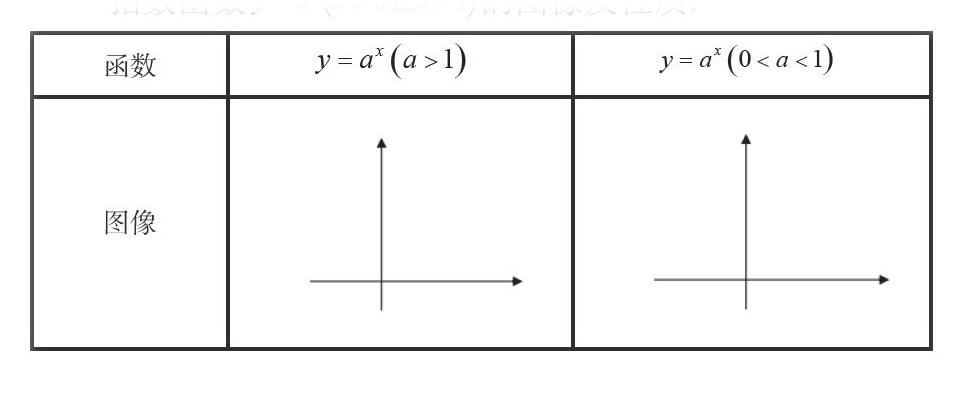
1、提出问题,指数函数图像如何?有哪些性质,要求学生用描点法绘制几个具体的函数图像 , , , , ,
3、几何画板演示以上函数图像,引导学生发现指数函数可以根据底数 分为两大类进行研究
设计意图:1、让学生体会研究一个具体的函数可以也应该从多个角度入手,图象能直观的看出函数的一些性质
2、底数进行分类是本课的一个难点,让学生在讨论中自己解决分类问题使该难点的突破显得自然。
(四)由特殊到一般----归纳数图像及性质
2、培养学生的抽象概括、归纳能力,以及语言表达能力。
(五)例题分析---学以致用
例,比较下列各题中的两个值的大小
① 与 ② 与 ③ 与
例2:已知下列不等式 , 比较m,n的大小 :
(1) (2) (3) ( )
设计意图:进一步理解指数函数图像及性质体会由形到数,由数到形,使学生再次体会数形结合思想、分类讨论思想
(六)当堂检测---反馈思考
1、 已知 ,则 的大小关系是______。
2、比较下列各题中两值的大小
(1) 与 (2) 与 (3) 与
设计意图:使学生养成及时回顾总结、反思的良好学习习惯和行为习惯。

