基于6-SPU并联机构的铆孔机器人静力学分析

梁诤 许勇 吕叶萍

摘要：对基于6|SPU六自由度并联机构的集制孔与铆接为一体的新型步行式铆孔机器人进行静力学分析：在位置逆解建模、求解的基础上，根据机器人铆接轨迹规划，确定铆枪的正确铆孔作业位姿;针对飞机某大型薄壁圆柱面工件，应用有限元分析软件进行机器人铆孔作业仿真，获得各铆接点工位对应的动平台各向最大变形量及机构的最大等效应力.仿真结果表明，机器人最大变形量最大值为51.847×10-7m，在飞机铆接制孔误差允許范围内，且机构最大等效应力最大值为2.698 MPa，远小于材料屈服极限，可满足铆孔作业的精度与强度需求.

Abstract：A new walking riveting robot integrating hole making and riveting based on 6|SPU six degrees of freedom parallel mechanism was analyzed statically.On the basis of inverse position modeling and solution， the correct position of riveting hole of riveting gun was determined according to robot riveting trajectory planning.For aircraft large thin|walled cylindrical workpiece， the finite element analysis software was used to simulate the robot riveting operation，and the maximum deformation of the moving platform and the maximum equivalent stress of the mechanism were obtained. The simulation results showed that the maximum deformation of the robotwas 51.847×10-7m， which was within the allowable error range of aircraft riveting hole making， and the maximum equivalent stress of the mechanism was 2.698 MPa， which was far less than the material yield limit， which could meet the requirements of precision and strength of riveting hole operation.

关键词：铆孔机器人;轨迹规划;静力学分析;变形

Key words：riveting robot;trajectory planning;static analysis;deformation

中图分类号：TH122文献标识码：ADOI：10.3969/j.issn.2096-1553.2019.04.014

文章编号：2096-1553（2019）04-0096-06

0 引言

大型复杂飞机外形薄壁壁板在航空、汽车等工业制造中有着重要作用，但是大型薄壁零件通常存在变形的困扰，特别是在加工后所产生的翘曲变形是不可忽视的技术难题.由不同的原因引起的大型曲面薄壁零件变形包括弹性变形、塑性变形、热变形和残余应力变形，其中残余应力为零件变形的主要原因.传统工艺方法已经无法满足航空航天、汽车制造等高端制造业对大型薄壁复杂曲面工件的精密、高效、柔性加工等高端需求，因此，自动化铆接机器人正日益成为智能制造的主流装备.刚度是满足机器人作业单元的重要性能指标，它随机器人的位姿而变化[1]，因此需在机构设计阶段快速预估出机构刚度是否满足作业要求，以便为机械结构的详细设计提供必要的理论依据.

机构刚度对机构末端的位姿精度非常重要，是影响机器人定位精度的重要因素.窦永磊等[2]计入所有支链构件和关节的弹性，基于全变形雅可比矩阵，构造出多种混联机器人的半解析刚度模型，通过算例揭示了整机刚度在任务空间中随位形的变化规律.W.A.Cao等[3]提出了对过约束SCARA运动并联机构进行刚度建模的一种通用方法.张东胜等[4]针对基于2RPU/UPR机构的五自由度混联机器人，分别求解了并联、串联部分的静刚度模型，从构造系统的力旋量系和弹性变形协调条件入手，简单且快速地建立了混联机器人的整体刚度模型，并求解了整机静刚度在任务空间中随位形变化的分布图.张俊等[5]分别采用虚拟关节法和有限元法，计入Exechon并联模块各关节和支链体的柔性，通过推导动平台和支链装配体间的变形协调方程，构建出系统的弹性静力学模型，由系统方程抽取出动平台刚度矩阵，据此预估了Exechon并联模块在典型位姿和工作全域内的刚度性能.

上述各种刚度建模方法都较为复杂，且影响机构刚度的因素较多，难以考虑全面.王南等[6]利用有限元分析方法研究了两种3-RPS并联机构的变形情况，并将结果与考虑约束反力所构造的刚度模型计算结果相互验证，但所建立的有限元模型未考虑不同运动副间算法的区别.

李育文等[7]采用有限元方法基于ANSYS建立了6|UPS机床的有限元模型，分析了其工作空间内的刚度分布，并验证了其有限元模型的合理性，但未考虑机构处于不同位姿时的刚度变化.

笔者所在研究团队提出了一种基于6|SPU（S表示球面副、P表示移动驱动副、U表示万向铰）六自由度并联机构的集制孔与铆接为一体的可移动式机器人，团队成员刘文彩等[8]分析了机构的运动学性能.在此基础上，本文拟基于位置逆解进行铆枪轨迹规划，采用有限元分析的方法，在考虑机构不同位姿及各运动副算法的基础上，对机构刚度（即变形、应力应变）进行静力学分析，以期为6|SPU并联机构的优化设计提供理论依据.

1 基于位置逆解的铆枪轨迹规划

1.1 机器人构型

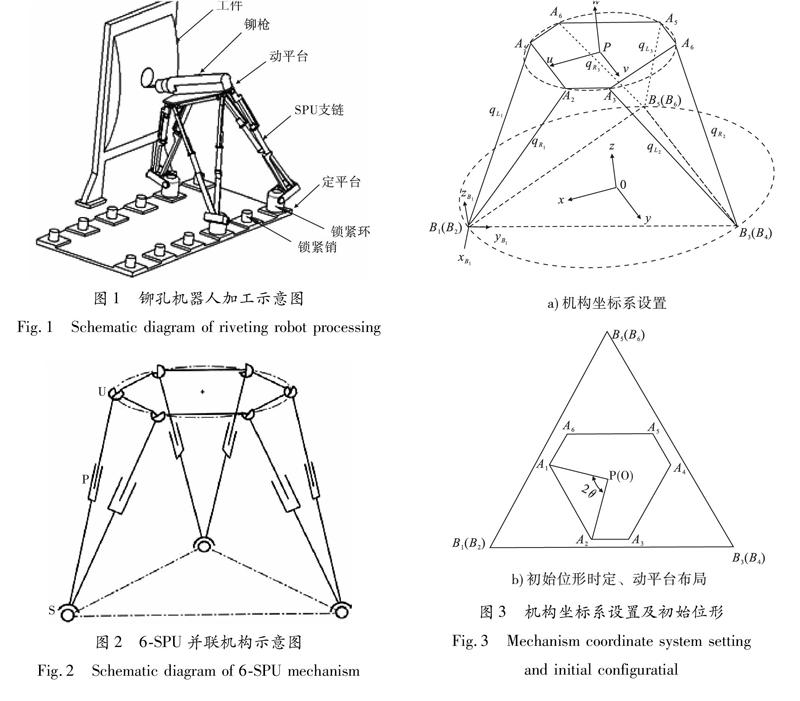
针对传统工艺协调复杂、流程冗长、加工范围受限等问题，设计了一种基于6|SPU并联机构的铆孔机器人，其加工示意图见图1.该机器人足端锁紧环可与定平台上的锁紧销可靠嵌入、脱离，实现摆腿/落腿运动，机器人行至目的工位时，动平台调姿，各足支撑于定平台，固结于动平台的铆枪执行加工任务.

本文提出的3闭环支链6|SPU并联机构如图2所示，每条支链（步行腿）均为一个含复合球面副S的2|SPU两自由度并联机构，可实现沿某一锁紧销队列的直线步行，且保持落足姿态恒与定平臺垂直.

1.2 位置逆解

机构坐标系设置及初始位形如图3所示.建立定平台坐标系{O-xyz}：坐标系原点O为等边三角形定平台的形心，x轴正方向由O指向复合球面副形心B1（B2），z轴正方向垂直定平台向上，y轴正方向由右手法则确定.建立动平台坐标系{P-uvw}：坐标系原点P为六边形动平台的形心，u轴正方向由P指向动平台上两万向铰形心A1和A2的连线中点，w轴正方向垂直动平台向上，v轴正方向由右手法则确定.以支链一为例说明建立支链坐标系{Bi-xBiyBizBi}（i=1，2，…，6，下同）的方法：坐标系原点取B1，yB1轴正方向由B1指向B3，zB1轴正方向垂直于B1B3B5所在平面且向外，xB1轴正方向由右手法则确定.

记定平台外接圆和动平台外接圆半径分别为rO和rP，动平台长边所对圆心角为2θ.机构初始位形为动平台、定平台平行，且动坐标系、定坐标系各坐标轴分别平行.

1.3 铆枪轨迹规划

本文以飞机某大型薄壁圆柱面工件表面铆接制孔为例，多个铆接孔形成的空间曲线即为铆枪末端轨迹.

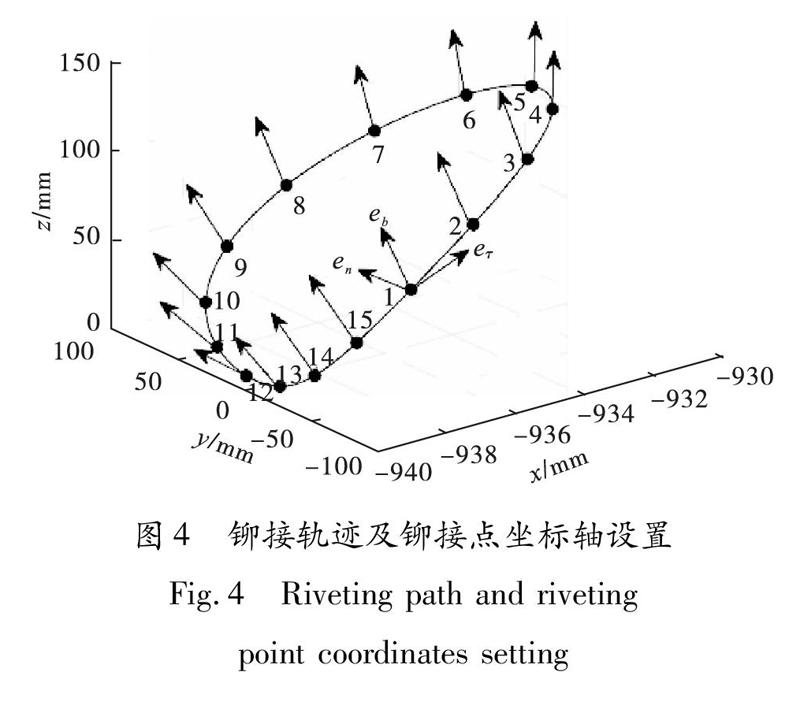
基于微分几何曲线论中的弗莱纳-雪列矢量[9]，可建立铆接点坐标系.运用Matlab软件计算出轨迹各点处的单位切向量τ，单位法向量n和单位次法向量b.为保证铆接制孔的加工精度，铆接作业时铆枪的前进方向必须与工件表面铆接点坐标系的τ方向一致，铆枪主轴方向必须与铆接点坐标系的b方向一致.铆接轨迹及铆接点处坐标轴设置如图4所示，各铆接点位置坐标及对应的铆枪主轴姿态角见表1.

2 6|SPU并联机构静力学分析

2.1 有限元分析前处理

并联机构的刚度模型是位形的函数，在应

用有限元软件对并联机构分析时，应针对不同位形对并联机构进行有限元分析[10].利用Solidworks软件建立机构的实体模型，将并联机构按照实际情况装配到一起.由表1通过位置逆解算得并联机构的位姿参数，将并联机构调整到需要的位姿并导入到Ansys Workbench中，在建模的过程中没有采用加权的方法.6|SPU并联机构在导入有限元分析软件之后，需根据运动副连接条件对每个零件设定接触约束，其中固定处采用bonded连接和MPC算法，移动副和转动副处采用No separation连接和Pure penalty算法，接触设定完成后，对装配体在定平台底面设定的约束为Fixed Support.每种并联机构的材料设定为structural steel，弹性模量E=200 GPa，密度为7850 kg·m-3，泊松比γ=0.3，屈服极限δ= 350 MPa.机器人整体模型采用四面体单元划分网格（见图5），不考虑应力走向，单元数目为27 968，节点数为80 397.设铆枪进行铆孔作业时承受沿铆枪轴线的轴向工作载荷F=110 N.

2.2 静力学分析

静力学分析可以全面、直观地评价机构的变形与应力分布情况[11].对机构进行静力学分析，其结果如图6和图7所示.

由图6可以看出，机构动平台在x，y，z方向最大变形量最大值分别为5.092×10-7m，27.586×10-7m和51.847×10-7m.机构平台在z方向最大变形量最大，说明机构在z方向的刚度低于其他两个方向，即在z方向承载能力较差;机构动平台在x方向的最大变形量最小，说明机构在x方向的刚度最好，即在x方向承载能力强于其他两个方向.通过查阅相关文献可知，飞机铆接制孔误差一般应控制在2×10-5m以内[8]，机构整体在x，y，z方向的最大变形量均小于该值，满足铆接加工的精度要求.

由图7可以看出，机构的最大等效应力最大值为2.698 MPa，远小于材料的屈服极限，能够满足铆接加工所需的强度要求.

分析过程中，机构在工作状态中产生的变形与等效应力较大的区域主要分布在动平台和驱动杆上，其他零件处的变形和应力均较小.

3 结语

针对高端制造业对大型薄壁复杂曲面工件的精密、高效、柔性加工需求，本文对基于6|SPU并联机构的新型步行式铆孔机器人进行了静力学分析.基于建模、求解机构位置逆解，完成了机器人铆接轨迹规划，确定了铆枪末端的精确轨迹和正确的铆孔作业姿态;以SolidWorks为平台对6|SPU并联机构进行三维建模，并运用有限元分析软件ANSYS中的Workbench模块对此机构的刚度进行静力学分析.结果表明：机器人最大变形量最大值为51.847×10-7m，在飞机铆接制孔误差允许范围内;机构最大等效应力最大值为2.698 MPa，远小于材料屈服极限.

该结果有力证明了本文提出的机构构型、位置逆解和轨迹规划模型的合理性，有限元分析结果也表明机构满足铆接加工精度与强度要求.该成果为自动铆接机器人的结构优化和性能分析提供了必要的理论依据.

根据文中静力学的分析结果，对自动铆接机器人变形和应力较大区域的零部件进行进一步的结构和尺寸优化，以提高自动铆接机器人的整体性能，将是下一步的工作重点.

参考文献：

[1] 汪满新，王攀峰，宋轶民，等.4自由度混联机器人静刚度分析[J].机械工程学报，2011，47（15）：9.

[2] 窦永磊，汪满新，王攀峰，等.一种6自由度混联机器人静刚度分析[J].机械工程学报，2015，51（7）：38.

[3] CAO W A，YANG D H，DING H F.A method for stiffness analysis of overconstrained parallel roboticmechanisms with Scara motion[J].Roboticsand Computer|integrated Manufacturing，2018（49）：426.

[4] 张东胜，许允斗，姚建涛，等.2RPU/UPR+RP五自由度混联机器人静刚度分析[J].中国机械工程，2018，29（6）：712.

[5] 张俊，赵艳芹.Exechon并联模块的静刚度建模与分析[J].机械工程学报，2016，52（19）：34.

[6] 王南，高鹏，崔国华，等.两种并联机构的静刚度及有限元分析[J].河北工程大学学报（自然科学版），2013，30（1）：87.

[7] 李育文，张华，杨建新，等.6|UPS并联机床静刚度的有限元分析和实验研究[J].中国机械工程，2004（2）：20.

[8] 刘文彩，许勇，陈佳丽，等.基于6|SPU并联机构的飞机壁板铆接机器人逆运动学分析[J].机械设计与研究，2018，34（2）：76.

[9] 应灿.焊接机器人工作站协同运动的轨迹优化研究[D].广州：华南理工大学，2013.

[10]王友渔，黄田，CHETWYND D，等.Tricept机械手静刚度解析建模方法[J].机械工程学报，2008（8）：13.

[11]张军，何芳.基于ANSYS一种转运小车关键件有限元分析[J].装备制造工艺，2016（10）：15.