改进的ACO|BP神经网络在锂离子电池SOC估算中的应用

王震 陆金桂

摘要：针对单一BP神经网络模型估算锂离子电池SOC易陷入局部最优的问题，引入蚁群算法ACO，并与BP神经网络模型相结合，提出了改进的ACO|BP神经网络以估算电池SOC.采用惯性矫正算法，在校正权阈值时加入惯性量，以改进BP神经网络;利用改进的全局信息素更新规则来改进ACO算法，以解决其易早熟收敛的问题.将经改进的ACO|BP神经网络应用于18650锂离子动力电池SOC估算，结果表明，改进的ACO|BP神经网络估算SOC的相对误差能控制在±1.957%以内，MAPE为0.897%，精度和稳定性明显优于单一BP神经网络和ACO|BP神经网络.

Abstract：Aiming at the problem that SOC of lithium ion batteries is easy to fall into local optimum by single BP neural network， ant colony algorithm was introduced and combined with BP neural network model，and an improvedACO|BP neural network was proposed to estimate battery SOC.Inertia correction algorithm was used to add inertia amount when correcting the weight threshold to improve BP neural network. ACO algorithm was improved using the improved global pheromone updating rules to solve the problem of premature convergence.The improved ACO|BP neural network was applied to estimate SOC of 18650 lithiumion power battery. The resultsshowed that the relative error of the improved ACO|BP neural network in estimating SOC could be controlled within ±1.957% and the MAPE was 0.897%. The accuracy and stability of the improved ACO|BP neural network were obviously better than those of single BP neural network and ACO|BP neural network.

关键词：电池SOC;蚁群优化;神经网络;估算模型

Key words：SOC of battery;

ant colony optimization;

neural network;estimation model

中图分类号：TM912文献标识码：ADOI：10.3969/j.issn.2096-1553.2019.04.012

文章编号：2096-1553（2019）04-0081-06

0 引言

动力电池SOC（state of charge）的估算是动力电池管理系统的核心.精确地估计动力电池SOC，一方面可以合理地分配能量，提高动力电池的续航时间，另一方面可以避免动力电池的过充和过放，安全保护动力电池，延长动力电池的使用寿命.如何精确地估算动力电池的SOC是业界当今研究的热点和难点.

目前国内外用于估算动力电池SOC的方法主要有安时积分法[1]、开路电压法[2]、扩展卡尔曼滤波法[3]、BP神经网络法[4]等.安时积分法虽然简单稳定，但是无法避免累计误差;开路电压法不能满足在线动态估算电池SOC的要求;扩展卡尔曼滤波法具有一阶泰勒精度[5]，但个别特征参数不稳定.

BP神经网络具有较强的自学习和非线性拟合能力，

而SOC与测量所得的电压、电流、温度等值之间是强烈的非线性关系，所以BP神经网络能够较好地估算动力电池的SOC.张传伟等[6]提出了BP神经网络估算SOC的模型;黄妙华等[7]改进了BP神经网络的SOC估算，利用较优的训练函数和传递函数提高了BP神经网络估算SOC的普适性.但单纯的BP神经网络法易陷入局部最优、收敛速度慢的情况.王鸽等[8]将蚁群算法（ACO）与BP神经网络结合，加快了网络的收敛速度，在一定程度上避免了单纯BP算法易出现局部极小值的问题，但是标准ACO算法仍存在易陷入局部最优的问题.

鉴于此，本文拟采用改进ACO算法优化改进后的BP神经网络，构建改进的ACO|BP神经网络，将其运用于锂电子电池的SOC估算，以期提高动力电池SOC的估算精度.

1 改进ACO|BP神经网络的构建

1.1 BP神經网络的改进

BP神经网络在训练过程中信号前向传播，误差逆向传播[9]，是通过模仿人类大脑神经网络构造、具有自适应和非线性拟合等能力的人工神经网络，其实质是通过不断修正神经网络各隐含层的各个权值和阈值，使误差达到设置的范围.估算SOC的BP神经网络由3层网络结构构成，即输入层、隐含层和输出层.

为了提高BP神经网络估算的实时性和准确性，本文采用惯性校正算法来改进BP神经网络，即在校正权阈值时，在本次误差计算得到的校正量的基础上，以一定的惯性系数加上前一次权阈值的校正量，作为此次的校正量.其计算公式为

其中，ΔW（n）为本次最终校正量;W为误差计算得到的校正量;αΔW（n-1）为惯性量，α是取值为（0，1）的惯性系数，ΔW（n-1）为前一次权阈值最终校正量.

相较于标准BP神经网络，经改进的BP神经网络其学习收敛速度和精度有较大的提高[10].

1.2 ACO算法的改进

ACO算法是一种仿生智能随机搜索算法.蚂蚁的觅食行为是一种强化正确行为的正反馈，而优先选择信息素浓度较高的路径则是该正反馈的前提，所有待优化问题的解空间对应整个蚂蚁群体的所有路径，较优蚂蚁（即行进路径较短的蚂蚁）释放较多的信息素，一段时间以后，该路径上累积了较高浓度的信息素，在正反馈的作用下选择此条路径的蚂蚁数量相应增多，如此循环，最终在最佳路径上集中了数量最多的蚂蚁[11]，此时该最短路径即为最优解.

由于蚁群系统是通过信息素的累积将搜索行为集中到最优解附近来寻优的，当局部最优解附近已经有较高浓度信息素时，绝大多数蚂蚁会选择局部最优解的路径，在正反馈的作用下易造成早熟收敛的行为，导致最终得到的是局部最优解而不是全局最优解.

本文拟通过改进ACO算法的全局信息素更新规则来避免蚁群陷入局部最优解，改进的全局信息素更新规则

是：通过增强蚁群目前最优解的信息素，削弱之前局部最优解信息素的方法，可以避免蚁群算法陷入局部最优解的问题，即为

1.3 ACO|BP神经网络的改进

设BP神经网络有K个权值，根据权值的取值范围将每个参数Ki（1≤i≤K）的定义域平均划分成L个区间，即每个区间的长度被L等分，从而形成一个K×L大小的集合A.将区间的临界值或选择区间中的随机值作为候选值.蚂蚁在集合A中遍历.计算蚂蚁经过的路径，分别选出最优和最差的蚂蚁，然后更新调节信息素，循环以上步骤直到达到最大循环次数，找出使得权值最合适的节点所在.所得到的解即是较优解.将此较优解作为BP神经网络算法权值的初始值.训练BP神经网络，对误差进行反馈调节，调整权值，得到最优解.算法流程图如图1所示，具体步骤如下.

步骤1 参数初始化：将每个权值和阈值的定义域等分，设置有m个蚂蚁，信息挥发系数ρ，信息素残留系数λ，信息素强度Q，最大迭代次数Nmax，BP神经网络全局误差E，最大学习次数N.

步骤2 权值选择：m只蚂蚁根据状态转移概率函数选择路径，蚁群迭代一次则完成一次解的构造，状态转移概率函数为

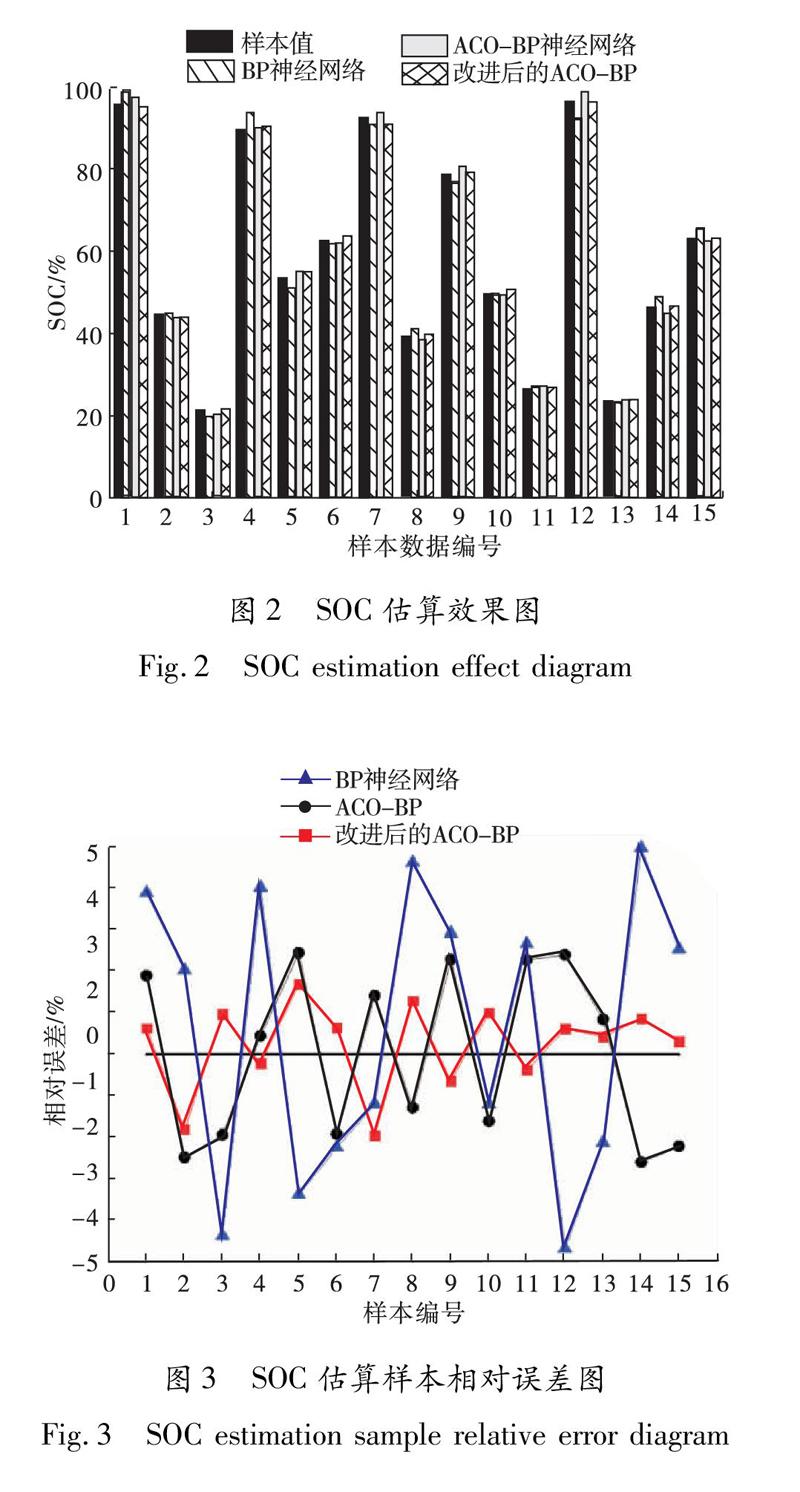
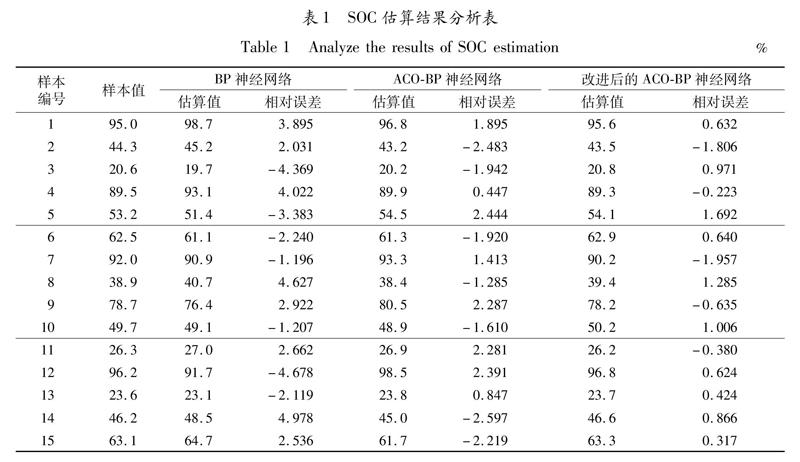
步骤3 若k

步骤4 将蚁群迭代得到的解作为BP神经网络的初始权值对网络进行训练，将BP神经网络的输出均方差最小值作为蚁群算法较优解.

步骤5 一个循环结束后，根据公式②③对残留信息进行全局更新，并重置信息表.

步骤6 若达到最大循环次数则输出较优权值，否则跳转至步骤2重复以上步骤.

步骤7 将蚁群迭代得到的较优解作为BP神经网络的初始权值进行训练，根据输出值与实际值的误差进行反馈调节，得到最优权值.

2 改进后的ACO|BP神经网络在电池SOC估算中的应用

2.1 输入层建模

神经网络输入参数的选择一般按照输入参数和输出参数相关性大、输入参数较易测量或提取、各输入参数之间相关性越小越好的原则进行.影响电池SOC的因素很复杂，其中电池的端电压、充放电电流和工况温度与SOC有极大的关系且较容易测得，故将其作为输入.因为有3个输入量，所以输入层节点数为3.

2.2 隐含层建模

多隐含层训练的复杂度高，训练所需的时间长，虽然估算精度高，泛化能力强，但是会增大过拟合的可能性.本文选用单隐含层的神经网络实现电池SOC的估算.

隐含层节点数根据经验公式大致确定为

其中，N为隐含层节点数，m为输入层节点数，n为输出层节点数，a为区间[0，10]之间的常数.

将每一个可能的隐含层节点数代入BP神经网络进行训练，选取最小误差值的隐含层节点数为5.

2.3 输出层建模

电池SOC的估计值是输出层的唯一项，所以输出层节点数为1.

2.4 确定学习速率

学习速率过大，网络训练时间缩短，牺牲了BP神經网络训练的收敛性，如果预期提高估算精度，则需降低学习速率，但是易造成网络收敛速度慢，训练时间过长[12].通过不断调整BP神经网络训练中的学习速率，选取最适合本模型的学习速率为0.01.

2.5 数据归一化处理

由于电压、电流和温度不是同一个量纲，本文将训练样本和估算样本数据通过最大最小法进行归一化处理，将样本数据归一化为无量纲数据[13].数据归一化函数形式为

3 仿真结果与分析

本文测试对象为额定电压3.7 V，容量为2.9 Ah的18650动力电池单体.分别测得该电池在0.5 C，1 C，1.5 C的放电率下恒流放电的电压、电流和温度数据.随机取100组数据作为训练样本，15组数据作为测试样本.为了验证本文改进后的ACO|BP神经网络估算电池SOC的准确性，将其与单一BP神经网络、ACO|BP神经网络估算结果进行对比.通过仿真实验，三者的估算效果、估算数据与样本数据误差分别如图2，图3和表1所示.

由图2可以看出，改进后的ACO|BP神经网络估算SOC的结果明显比单一BP神经网络和ACO|BP神经网络的估算结果更逼近样本数据值.由图3和表1可以看出，改进后的ACO|BP神经网络训练结果的相对误差在±1.957%以内，ACO输出层BP神经网络训练结果的相对误差在±2.597%以内，单一BP神经网络训练结果的相对误差在±4.978%以内.改进后的ACO|BP神经网络的相对误差范围明显小于标准ACO|BP和单一BP神经网络，表明改进后的ACO|BP神经网络估算电池SOC具有较高的精度和较高的稳定性.

为了更加直观地评价ACO|BP神经网络的估算能力，本文采用平均绝对值百分比误差（MAPE）进行分析，其计算公式为

其中，N为估算样本总数;Pf，i为第i个样本SOC估算值;Pa，i为第i个样本的样本值.由表1数据计算可得，改进后的ACO|BP神经网络、ACO|BP神经网络和BP神经网络的MAPE分别为0.897%，1.871%，3.124%，改进后的ACO|BP神经网络的估算精度明显优于单一BP神经网络和标准ACO|BP神经网络，证明了改进后的ACO|BP神经网络估算动力电池SOC的可行性.

4 结语

本文利用惯性校正算法优化BP神经网络，利用改进的全局信息素更新规则改进ACO算法，利用改进的ACO算法优秀的整体寻优能力，优化BP神经网络的初始权值，在一定程度上弥补了BP神经网络容易陷入局部最优的缺点.将改进后的ACO|BP神经网络模型用于动力电池SOC估算，使得估算误差明显减小.与单一BP神经网络、标准ACO|BP神经网络估算结果对比发现，其在逼近能力方面明显更优，精度更高，故本模型有较好的准确性和合理性.深入研究影响电池SOC的因素，如循环次数、充电倍率和内阻等，以进一步提高电池SOC的估算精度，将是下一步的工作重点.

参考文献：

[1] 欧阳剑，李迪，柳俊城.电动汽车用动力电池荷电状态估算方法研究综述[J].机电工程技术，2016，45（1）：52.

[2] 李争，智若东，孙宏旺，等.基于开路电压预测的SOC估算方法[J].河北工业科技，2017，34（1）：36.

[3] 王宇航，王顺利，潘小琴，等.基于扩展卡尔曼的锂离子电池SOC估算研究[J].自动化与仪表，2018，33（8）：76.

[4] 赵钢，朱芳欣，窦汝振.基于PSO|BP

的电动汽车锂离子

电池SOC估算[J].电源技术，2018，42（9）：1318.

[5] 欧阳剑.电动汽车用锂离子动力电池SOC估算和SOF评估的研究[D].广州：华南理工大学，2016.

[6] 张传伟，李林阳，赵东刚.基于BP神经网络法估算动力电池SOC[J].电源技术，2017，41（9）：1356.

[7] 黄妙华，严永刚，朱立明.改进 BP 神经网络的磷酸铁锂电池 SOC 估算[J].武汉理工大学学报（信息与管理工程版），2014（6）：790.

[8] 王鴿，蒲蓬勃.ACO|BP在神经网络训练中的研究与应用[J].计算机仿真，2009，26（12）：136.

[9] 赵钢，孙豪赛，罗淑贞.基于BP神经网络的动力电池SOC估算[J].电源技术，2016，40（4）：818.

[10]李东玉，王睿，冯宜民.基于BP神经网络的阀控铅酸盐蓄电池劣化程度预测[J].郑州轻工业学院学报（自然科学版），2012，27（4）：12.

[11]孙启豪，蔡爱华.航空搜潜布阵航路优化研究[J].电光与控制，2017（4）：39.

[12]霍健.大跨径连续梁桥悬臂施工线形控制[D].哈尔滨：东北林业大学，2013.

[13]周美兰，王吉昌，李艳萍.优化的BP神经网络在预测电动汽车SOC上的应用[J].黑龙江大学自然科学学报，2015，32（1）：129.