数形结合思想在初中数学教学中的应用与探究
白文娟
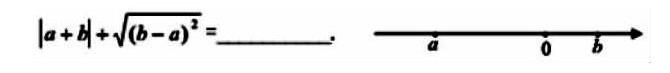

摘要:初中数学教学的任务之一是对学生思维方式和思考角度的挖掘和探索,教师在教学过程中对于学生数形结合思想的开拓与培养不仅一个重要的教学目标,同时对形成新的思维习惯有重要作用,对学生整体学习有很大的帮助。
关键词:数形结合思想;初中数学教学
中图分类号:G633.6文献标识码:B 文章编号:1672-1578(2019)32-0158-02
数形结合简单来说就是指将图形灵活运用到数学这门学科学习过程中,将数学这种具有抽象性和逻辑性学科用图形给表现出来。初中数学教学面对的是初中生,数学教师应该在这个过程中充分了解他们的心智和心理,初中生在这个阶段逻辑思维能力和抽象理解能力还没有很发达,因而数形结合这种学习思想适合初中生学习数学,同样数学老师们应该积极引导学生掌握并且灵活运用这种思维方式,从而使学生们可以更好地进行学习。
1.数形结合思想
1.1 数形结合思想特点以及数学教学的特点。
数形结合思想主要可以分为两个方面来进行解释,首先是“数”,这个概念主要是指某项事物的面积、体积以及容积等数量,其次对于“形”,这个概念主要是指某项事物的图形外观,将这两概念结合在一起,我们就可以简单理解成将离散的数字用直线组成的图形表现出来,在图形中我们可以看见数字之间具备的关系,充分将两者融为一体,这样就将具有形象性与生动性。对于初中数学的抽象性与逻辑性,同时在初中生的心智和心理还未成熟的前提下,这些在一定程度上构成了数学教学的难度,因而进行探索新型数学学习方法显得非常有必要。
1.2 数形结合思想的必要性和重要性。
对于上文中我们已经知道初中数学具有非常强的抽象性和逻辑性,同时在认识到初中生的未成熟心智和心理下,数形结合这个重要的思维方法和思想模式的出现无疑给学生学习数学提供了一个新的思路和角度,数形结合这个思想使学生们重现认识到数字与图形间的关系,例如在函数中,在一个非常复杂函数公式中包含很多数字和公式,学生们首先看时可能不能马上理解其含义,但是如果将之用图像表现出来,这是复杂的函数关系就显得很简单和容易,这些都说明数形结合思想运用到初中数学中具有必要性和重要性。
2.数形结合思想在初中数学教学中的应用与探究
数形结合思想在初中数学教学中非常有必要,在下文中将从几个方面进行详细说明:
2.1 实数正负的确定是典型的数形结合思想的运用。
對于实数的正负来说,如果一直用大于、小于符号表示的话,学生可能没有一个非常直观的理解,如果老师在教学过程中充分使用数轴来确定实数正负就显得非常简单而且方便。
例如:在上题中,我们可以知道图形中a、b的正负性质,图形中包含意义就是指:a是负数,b是正数,-a的值是比b的值大,由此可知上题答案是-2a数学中的实数都可以在数轴上显示出来,同时数轴上每一个点都表示一个具体数字值,这种就是典型的数形结合思想,将数字与图形有机融合,同时具体数字的相反数与绝对值也同样可以得知。
2.2 在几何中“空间与图形”中的数形结合思想。
几何图形的精髓就是用图形将一切事物表示出来,显得神秘而有趣。
例如下图中:
平行四边形 菱形
在初中数学中学生们学习的几何图形大多都是简单的三角形、长方形以及正方形等,对于这些图形的性质,例如说各条边和各个角之间的关系我们都可以通过具体图形来进行表示,看到平行四边形学生们自然知道对边平行且相等,这些都是比较简单的抽象思维,对于菱形来说它们之间的转化而导致的各种性质的改变,这时同样可以通过图形来表示,这样就可以将复杂的数据用图形展示,显得形象而生动。
2.3 解不等式中的数形结合的有效运用。
在对于不等式来说,老师在教学过程中最重要的就是教授学生学会使用数轴确定范围,这个数轴由上文中可以知道不等式的范围,这是对于数轴在数学学习中的又一次使用,如下文所示:
要求一:a<5或者a>8
要求二:3 对于这个题目来说,学生就可以使用数轴,首先对于要求一在数轴上体现,在将要求二在数轴上体现,这样就可以在数轴上取出两者的交集,从而划分出a的范围: 3 2.4 在方程中数形结合思想的运用。 在初中数学中方程式的解答是一个非常重要的知识点,因而老师们在教学过程中运用数形结合解决方程式问题非常重要而且必要。如下文所示: 在这个由x、y两条数轴线组成的坐标轴,在初中数学中所有的方程式都可以在这个坐标轴中得到体现,例如:解方程式:2x+y=3 (1)x-y=0 (2)对于这样一个方程式来讲,我们就可以在上述坐标轴中分别画出两条直线,在坐标周轴中两条直线有一个交点,就是A(1,1)这里横纵坐标表示x、y的值,由此得出x=1 y=1将方程式充分与坐标轴将结合对于初中学生学习方程有很大的帮助。 2.5 在函数问题中数形结合的运用。 如下文所示: 二次函数式一次函数式 在初中数学中可以算是一次函数和二次函数难度最大,同样理解难度也是相当大的。首先是一次函数的代表关系是y=kx+b(k≠0)中k、b的正负是与一次函数在坐标轴的位子有 密切的联系,对于二次函数来说y=ax -bx+c是其代表关系式,其中a、b、c在图形中都可以找到根据,在图中也可以得出相应的数据,具体数据都可以在图中标出。 3.结束语 综上所述,数形结合思想简单来说就是将图形与数学密切结合,将数字转化为图形,从图形中得出有效数据,初中数学教学中充分运用数形结合思想将使学生灵活思考,愉快学习。 参考文献: [1]张志华.在初中数学中挖掘数形结合思想[J].科普童话,2016(24):34. [2]张旭华.初中数学教学中渗透数形结合思想的研究[J].考试周刊,2017(35):62. [3]陈玉娟.数形结合思想贵在“结合”—一类问题错解引发的思考[J].数学通报,2018(10):38-41+50. [4]李晓琴.“数形结合”在初中数学中的“第一次碰撞”——“数形结合”在有理数中的运用[J].新作文(教育教学研究),2017(24):42-43.

