多项式混沌展开和最大熵原理的结构动力特性不确定性量化

万华平 邰永敢 钟剑

摘要： 结构参数不可避免存在不确定性，参数不确定性必然会导致结构动力特性具有不确定性。 量化动力特性不确定性能为结构分析与设计提供准确的动力信息，因此发展快速有效的不确定性量化方法非常必要。提出了一种基于多项式混沌展开和最大熵原理的不确定性量化方法，用于定量参数不确定性传递到结构动力特性不确定性的大小。具体是，多项式混沌展开替代模型用来取代耗时的结构有限元模型，并实现解析地计算出结构动力特性的高阶统计矩，然后利用统计矩信息并结合最大熵原理推断出结构动力特性的概率密度函数的解析表达式。最后以一简支钢桁架桥为例，验证多项式混沌展开和最大熵原理的结构动力特性不确定性量化方法的有效性。

关键词： 动力特性; 不确定性量化; 多项式混沌展开; 最大熵原理; 统计矩

中图分类号： O324; TB123 文献标志码： A 文章编号： 1004-4523（2019）04-0574-07

DOI：10.16385/j.cnki.issn.1004-4523.2019.04.003

引 言

結构动力特性（如固有频率）对于结构的动力设计和振动分析等均具有重要意义，因此准确表征结构的动力特性非常重要。结构参数的真实值往往很难获得，引起结构参数不确定性的来源主要包括材料参数和几何参数不确定性、边界条件参数的不确定性以及结构外荷载的不确定性等[1]。结构参数不确定性会导致结构动力特性具有不确定性（变异性），欲得到准确的结构动力特性信息，参数不确定性对动力特性的影响不应忽略。 定量参数不确定性传递到结构动力特性的不确定性是结构动力分析领域一个重要研究，即结构动力特性不确定性量化[2-3]。

结构动力不确定性量化的目的是为了定量参数不确定性引起的结构动特性不确定性大小，表征动力特性不确定性的量包括统计矩（比如均值、方差）、上下限（或者包络）和概率密度函数等。蒙托卡罗模拟（Monte Carlo Simulation， MCS）方法是量化结构动力不确定性最为常用的方法，具有易于实现、稳定性好等优势。MCS 方法是对不确定性参数进行大量采样，然后计算每次采样值对应的动力特性，最后对所获的动力特性样本进行统计。由于工程结构大多数很复杂和尺寸大，其有限元模型往往很庞大，MCS 方法因高昂的计算花费而很难应用于工程实际[4-5]。摄动法[6-8]和区间分析法[9-12]在结构动力特性量化研究领域得到广泛应用，它们是基于结构动力方程（涉及质量、刚度和阻尼矩阵）进行分析计算，然而复杂结构有限元模型一般是借助商用有限元软件建立的，提取结构的系统矩阵并进行后续的迭代计算非常困难。 替代模型（Metamodel）成为解决复杂结构动力不确定性量化的有效手段，其采用低维的和显式的近似数学模型取代耗时的有限元模型，然后在替代模型框架下进行不确定性量化分析。

多项式混沌展开（Polynomial Chaos Expansion， PCE）模型是在概率框架下建立的，是具有显式表达式的参数化模型，在工程领域得到了广泛应用[13-15]。多项式混沌展开模型是一种正交多项式，用于响应统计矩计算具有非常大的优势，响应统计矩（如均值和方差）可以根据模型系数解析求出。本文基于多项式混沌展开这一优势，将多项式混沌展开代替有限元模型来进行结构动力不确定量化分析[13]。本文的主要工作包括两部分： （1） 建立适用于随机参数服从任意概率分布的多项式混沌展开模型，然后解析地求出动力特性的高阶统计矩，并不只限于一阶和二阶统计矩（即均值和方差）; （2） 基于得到的统计矩信息，采用最大熵原理（Maximum Entropy Principle，MEP）方法推断动力特性的概率密度函数，概率密度函数为动力特性提供更丰富的不确定性信息。 最后用一简支钢桁架桥算例演示本文提出的基于多项式混沌展开和最大熵原理的结构动力特性不确定性量化方法，并通过对比 MCS 方法计算结果来验证本文方法的有效性。

1 基于多项式混沌展开的统计矩计算

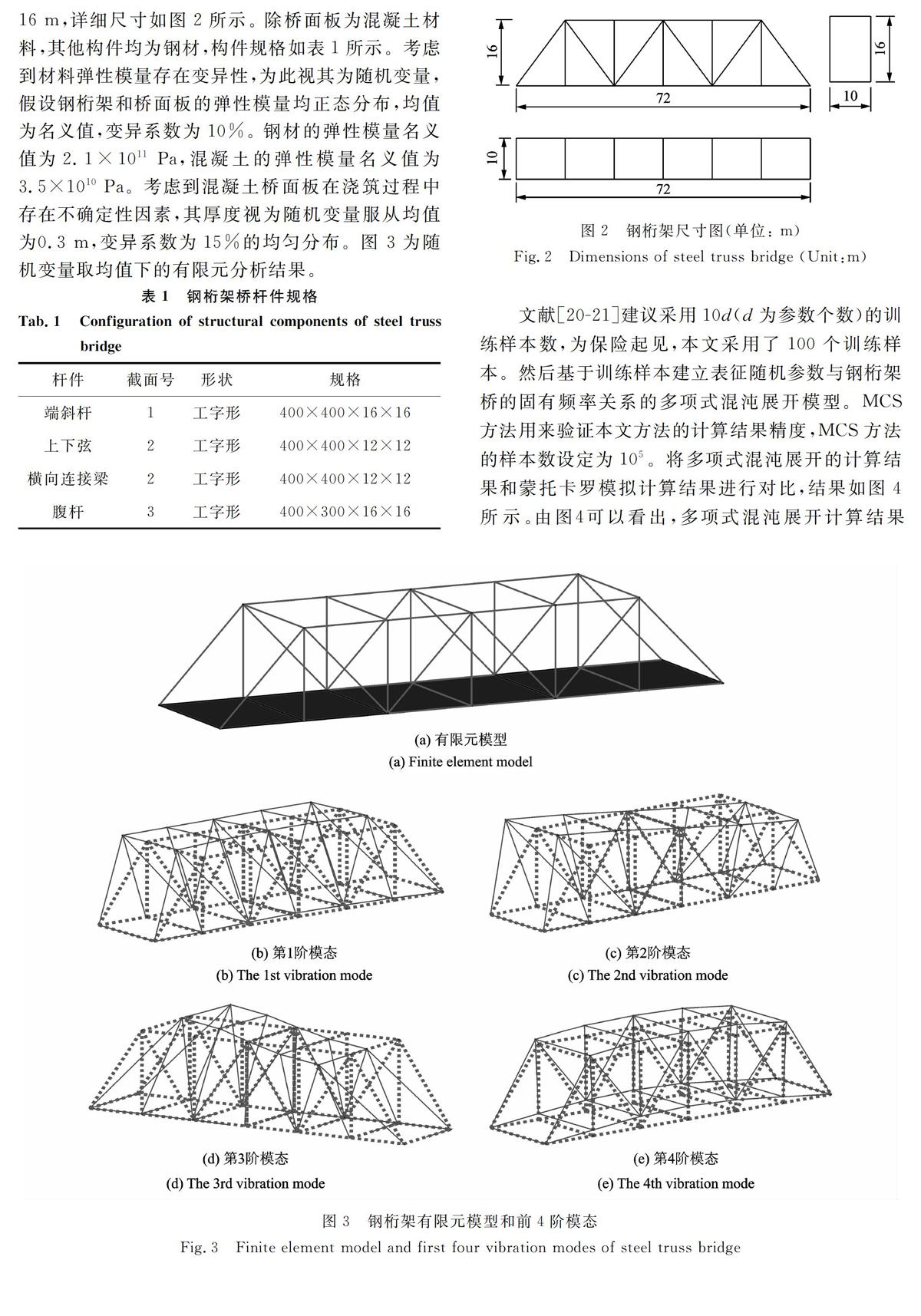
用一下承式简支钢桁架桥验证基于多项式混沌展开的高阶统计矩计算和最大熵概原理的率密度函数估计的正确性。 钢桁架桥长72 m，宽10 m，高16 m，详细尺寸如图2所示。 除桥面板为混凝土材料，其他构件均为钢材，构件规格如表1所示。考虑到材料弹性模量存在变异性，为此视其为随机变量，假设钢桁架和桥面板的弹性模量均正态分布，均值为名义值，变异系数为10%。 钢材的弹性模量名义值为2.1×1011 Pa，混凝土的弹性模量名义值为3.5×1010 Pa。考虑到混凝土桥面板在浇筑过程中存在不确定性因素，其厚度视为随机变量服从均值为0.3 m，变异系数为15%的均匀分布。图 3为随机变量取均值下的有限元分析结果。

文献[20-21]建议采用10d（d为参数个数）的训练样本数，为保险起见，本文采用了100个训练样本。然后基于训练样本建立表征随机参数与钢桁架桥的固有频率关系的多项式混沌展开模型。MCS方法用来验证本文方法的计算结果精度，MCS方法的样本数设定为105。将多项式混沌展开的计算结果和蒙托卡罗模拟计算结果进行对比，结果如图4所示。由图4可以看出， 多项式混沌展开计算结果和蒙托卡罗模拟计算结果吻合的非常好，几乎没有差别，最大相对误差为 0.7538%，表明用于高阶统计矩计算的多项式混沌展开方法精度非常高。高精度的统计矩对基于最大熵原理的动力特性的概率密度函数的估计具有重要意义。接下来将利用计算得到的结构动力特性前4阶统计矩结合最大熵原理得到结构动力特性概率密度函数。同样的蒙托卡罗模拟方法用来验证概率密度函数估计结果的准确性，如图5所示。同样地，由图5可知基于最大熵原理得到的钢桁架桥动力特性的概率密度函数与蒙托卡罗模拟结果非常吻合，说明本文方法用于动力特性的概率密度函数估计精度很高。该数值桁架桥一次特征值分析仅需要0.042 s，MCS方法总耗时约为70 min，而本文方法仅1 min左右。需要指出的是当模型越复杂，有限元分析越耗时，本文方法计算效率优势则更为明显。综合上述结果，表明本文提出的多项式混沌展开和最大熵原理相结合的方法在结构动力特性不确定性量化应用中的有效性。

4 总 结

本文提出了一种多项式混沌展开和最大熵原理相结合的不确定性量化方法，该方法包括基于多项式混沌展开的高阶统计矩计算和基于最大熵原理的概率密度函数估计两部分内容。该方法首先利用多项式混沌展开模型替代原先的复杂的结构系统，用于表征结构系统的不确定性参数与动力特性的映射关系; 然后在替代模型框架下，利用多项式混沌展开系数与单变量数字统计特征的组合关系快速有效地计算出结构动力特性的高阶统计矩; 接着将获得的动力特性的高阶统计矩信息作为约束条件，利用最大熵原理估计结构动特性的概率密度函数。最后用一简支钢桁架桥算例演示和验证本文方法，该桁架桥的前4阶固有频率为目标量。采用本文方法可快速计算得到固有频率的高阶统计矩和概率密度函数，其计算结果与蒙特卡罗方法对比。对比结果表明： 基于多项式混沌展开技术得到的高阶统计矩结果的精度非常高，最大相对误差仅为 0.7538%; 以高階统计矩信息为约束条件，基于最大熵原理推断的固有频率的概率密度函数与蒙特卡罗方法估计的结果非常吻合。因此，本文提出的基于多项式混沌展开和最大熵原理相结合的方法的计算精度非常高，能够用于结构动力特性不确定性量化研究。

参考文献：

[1] 万华平.结构动力不确定性及其随机模型修正方法研究[D].长沙：中南大学， 2014.

Wan H P. Study on uncertainty in structural dynamics and stochastic model updating[D]. Changsha： Central South University， 2014.

[2] Ibrahim R A. Structural dynamics with parameter uncertainties[J]. Applied Mechanics Reviews， 1987，40（3）：309-328.

[3] Mace B R， Worden K， Manson G. Uncertainty in structural dynamics[J]. Journal of Sound and Vibration， 2005，288（3）：423-429.

[4] Wan H P， Mao Z， Todd M D， et al. Analytical uncertainty quantification for modal frequencies withstructural parameter uncertainty using a Gaussian process metamodel[J]. Engineering Structures， 2014，75：577-589.

[5] Wan H P， Ren W X， Todd M D. An efficient metamodeling approach for uncertainty quantification of complexsystems with arbitrary parameter probability distributions[J]. International Journal for Numerical Methods in Engineering， 2017，109（5）：739-760.

[6] 陈塑寰，张宗芬.结构固有频率的统计特性[J].振动工程学报，1991，4（1）：90-95.

Chen S H， Zhang Z F. Statistics of structural natural frequeneies[J]. Journal of Vibration Engineering， 1991，4（1）： 90-95.

[7] 刘春华，秦 权.桥梁结构固有频率的统计特征[J]. 中国公路学报， 1997，10（4）：50-55.

Liu C H， Qin Q. Statistics of natural frequencies for bridge structures[J]. China Journal of Highway and Transport， 1997，10（4）：50-55.

[8] 王新堂， 梅占馨.随机参数冷却塔的随机特征值样条子域随机摄动分析[J].计算力学学报，1997，14（2）：174-181.

Wang X T， Mei Z X. Random eigenvalue analysis of cooling tower on the spline subdomain random perturbation methods[J]. Chinese Jouranal of Computational Mechanics， 1997，14（2）：174-181.

[9] Qiu Z P， Wang X J， Friswell M I. Eigenvalue bounds of structures with uncertain-but-bounded parameters[J]. Journal of Sound and Vibration， 2005，282（1-2）：297-312.

[10] 王登刚， 李 杰. 计算具有区间参数结构特征值范围的一种新方法[J]. 计算力学学报， 2004，21（1）：56-61.

Wang D G， Li J. A new method for computing the eigenvalues bounds of structures with interval parameters[J]. Chinese Journal of Computational Mechanics， 2004，21（1）：56-61.

[11] 陈怀海， 陈正想. 求解实对称矩阵区间特征值问题的直接优化法[J]. 振动工程学报， 2000，13（1）：117-121.

Chen H H， Chen Z X. A direct optimization method for solving eigen problems of interval matrices[J]. Journal of Vibration Engineering， 2000，13（1）：117-121.

[12] Wang C， Gao W， Song C M， et al. Stochastic interval analysis of natural frequency and mode shape of structures with uncertainties[J]. Journal of Sound and Vibration， 2014，333（9）：2483-2503.

[13] Wu S Q， Law S S. Evaluating the response statistics of an uncertain bridge-vehicle system[J]. Mechanical Systems and Signal Processing， 2012，27：576-589.

[14] 彭勇波，李 杰.基于正交展开方法的 Duffing振子随机最优控制[J]. 振动工程学报， 2011，24（4）：333-339.

Peng Y B， Li J. Orthogonal expansions based stochastic optimal control of Duffing oscillators[J]. Journal of Vibration Engineering， 2011，24（4）：333-339.

[15] 方圣恩， 张秋虎， 林友勤， 等. 不确定性参数识别的区间响应面模型修正方法[J]. 振动工程学报，2015，28（1）：73-81.

Fang S E， Zhang Q H， Lin Y Q， et al. Uncertain parameter identification using interval response surface model updating[J]. Journal of Vibration Engineering， 2015，28（1）：73-81.

[16] Xiu D. Numerical Methods for Stochastic Computations： A Spectral Method Approach[M]. Princeton： Princeton University Press， 2010.

[17] Jaynes E T.Information theory and statistical mechanics[J].Physical Review，1957，106（4）：620-630.

[18] Gotovac H， Gotovac B. Maximum entropy algorithm with inexact upper entropy bound based on Fup basis functions with compact support[J]. Journal of Computational Physics， 2009，228：9079-9091.

[19] Deng Y， Ding Y L， Li A Q， et al. Prediction of extreme wind velocity at the site of the Runyang suspension bridge[J]. Applied Physics & Engineering， 2011，12（8）：605-615.

[20] Konakli K， Sudret B. Polynomial meta-models with canonical low-rank approximations： Numerical insights and comparison to sparse polynomial chaos expansions[J]. Journal of Computational Physics， 2016，321：1144-1169.

[21] Qiujing P， Daniel D. Sliced inverse regression-based sparse polynomial chaos expansions for reliability analysis in high dimensions[J]. Reliability Engineering & System Safety， 2017， 167： 484-493.

Abstract： Structural parameters inevitably involve uncertainty， and the uncertainty of parameters will lead to the variability in the structural dynamic characteristics. Quantification of uncertainty in dynamic characteristics is able to provide accurate dynamic information for structural analysis and design. Therefore， developing a rapid and effective uncertainty quantification （UQ） method is very necessary. This paper proposes an efficient UQ method with combination of polynomial chaos expansion （PCE） and maximum entropy principle （MEP） to measure the uncertainty in dynamic characteristics propagated from parameter uncertainty. Specifically， the PCE surrogate model is used to replace the time-consuming structural finite element model， and the high-order statistical moments of the structural dynamic characteristics are analytically calculated; the obtained statistical moment information and the MEP are used to deduce the probability density function of structural dynamic characteristics. Finally， a simple-supported steel truss bridge is provided to verify the feasibility of the proposed method in UQ for structural dynamic characteristics.

Key words： dynamic characteristics; uncertainty quantification characteristics; polynomial chaos expansion; maximum entropy principle; statistical moments

作者简介： 万华平（1986-）， 男， 副教授。电话： 15556928238;E-mail： huaping.wan@hftu.edu.cn

通讯作者： 任伟新（1960-）， 男， 教授，博士生導师。 E-mail： renwx@hfut.edu.cn